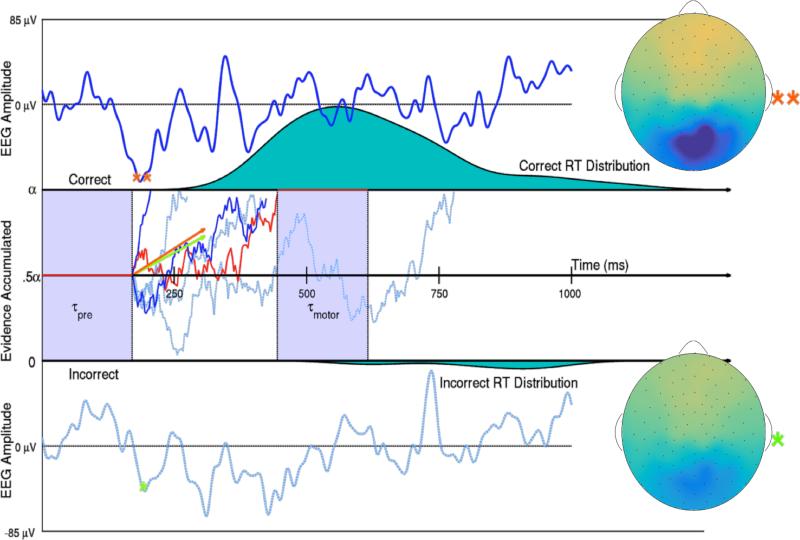
Figure 1.

Two trials of Subject 10's SVD weighted EEG (Top and Bottom with bounds −85 to 85 μV) and representations of this subject's evidence accumulation process on 6 low noise trials (Middle). Evidence for a correct response in one example trial (denoted by the red line) first remains neutral during an initial period of visual preprocessing time τ_pre. Then evidence is accumulated with an instantaneous evidence accumulation rate of mean δ (the drift rate) and standard deviation ς (the diffusion coefficient) via a Wiener process. The subject acquires either α = 1 evidence unit or 0 evidence units to make a correct or incorrect decision respectively. After enough evidence is reached for either decision, motor response time τ_motor explains the remainder of that trial's observed reaction time. The 85^th and 15^th percentiles of Subject 10's single-trial drift rates δ_i,10,1 in the low noise condition are shown as orange and green vectors, such that it would take 253 and 299 ms respectively to accumulate the .5 evidence accumulation units need to make a correct decision if there was no variance in the accumulation process. The larger drift rate is a linear function of the larger single-trial N200 amplitude (**), while the smaller drift rate is a linear function of the smaller N200 amplitude (*). The scalp activation (SVD weights multiplied by one trial's N200 amplitude) of this subject's response to the visual signal ranges from −13 to 13 μV on both trials. The two dark blue and red evidence time courses were randomly generated trials with the larger drift rate. The three dotted, light blue evidence time courses were randomly generated trials with the smaller drift rate. True Wiener processes with drifts δ_i,10,1 and diffusion coefficient ς_10,1 were estimated using a simple numerical technique discussed in Brown et al. (2006).