Positive Feedback Amplifies the Response of Mitochondrial Membrane Potential to Glucose Concentration in Clonal Pancreatic Beta Cells

Abstract

Analysis of the cellular mechanisms of metabolic disorders, including type 2 diabetes mellitus, is complicated by the large number of reactions and interactions in metabolic networks. Metabolic control analysis with appropriate modularization is a powerful method for simplifying and analyzing these networks. To analyze control of cellular energy metabolism in adherent cell cultures of the INS-1 832/13 pancreatic β-cell model we adapted our microscopy assay of absolute mitochondrial membrane potential (ΔψM) to a fluorescence microplate reader format, and applied it in conjunction with cell respirometry. In these cells the sensitive response of ΔψM to extracellular glucose concentration drives glucose-stimulated insulin secretion. Using metabolic control analysis we identified the control properties that generate this sensitive response. Force-flux relationships between ΔψM and respiration were used to calculate kinetic responses to ΔψM of processes both upstream (glucose oxidation) and downstream (proton leak and ATP turnover) of ΔψM. The analysis revealed that glucose-evoked ΔψM hyperpolarization is amplified by increased glucose oxidation activity caused by factors downstream of ΔψM. At high glucose, the hyperpolarized ΔψM is stabilized almost completely by the action of glucose oxidation, whereas proton leak also contribute to the homeostatic control of ΔψM at low glucose. These findings suggest a strong positive feedback loop in the regulation of β-cell energetics, and a possible regulatory role of proton leak in the fasting state. Analysis of islet bioenergetics from published cases of type 2 diabetes suggests that disruption of this feedback can explain the damaged bioenergetic response of β-cells to glucose.

1 Introduction

Mitochondrial metabolism of glycolytic pyruvate plays a central role in insulin secretion [1]. The canonical pathway of glucose-stimulated insulin secretion (GSIS) relies on hyperpolarization of mitochondrial membrane potential (ΔψM) (more strictly, hyperpolarization of the protonmotive force) leading to increased mitochondrial production of ATP, and is largely responsible for the first phase of insulin secretion [2–7]. Both type 1 and type 2 diabetes (T2D) in humans are characterized by early impairment of this phase [8–14], suggesting a possible role of disturbed cellular energy metabolism. While rare mitochondrial defects can cause diabetes [15], it is possible that more subtle derangements in cellular energy metabolism contribute more generally to β-cell impairment in diabetes. In support of this idea, the dampened response of ΔψM to glucose in T2D human β-cells may reflect a subtle bioenergetic supply-demand dysfunction [16].

Glucose stimulation of the β-cell changes virtually all variables of cellular energy metabolism, making it non-trivial to define which processes drive observed changes and which processes are responsible for deficiencies observed in disease. This is complicated by the large number of reactions in metabolic networks and the multiple interactions between them. Metabolic control analysis [17–19] with appropriate modularization is a powerful method for simplifying and analyzing these systems. Metabolic control analysis is a mathematical formalism to describe the control and regulation of metabolic systems; in particular, it can quantify how a change in a steady state is caused by changes in the activities of individual components of the system. Here, we reduce the complexity of β-cell energy metabolism to a simple modular system in which the modules of glucose oxidation, phosphorylation plus ATP turnover, and proton leak are linked by ΔψM as their common intermediate. Using this simplified system, the only measurements needed to describe the internal control structure and the regulation by external glucose are the fluxes through each module and the level of ΔψM.

Two complementary technologies make possible the measurement of these bioenergetic variables in adherent cell cultures. First, flux through each of the modules can be determined by measuring the extracellular oxygen consumption rate, where respiration is restricted by different combinations of mitochondrial inhibitors to report on a given module [20]. To this end, we used the Seahorse Extracellular Flux Analyzer, which utilizes our calibration algorithm [21], in conjunction with whole-well cell counting by fluorescence microscopy to normalize the measured rates. Second, we previously developed a method for determining absolute values of ΔψM in intact cells using fluorescence microscopy, allowing comparison between adherent cells in which plasma membrane potential (ΔψP) and morphological factors may differ [16,22]. To enable measurement of ΔψM in populations of cells in microplate samples, comparable to the populations used for cell respirometry, we introduce here a microplate reader-based adaptation of this method. Together, these technical advances allow measurement all of the variables required for metabolic control analysis of energy metabolism in adherent cells. This is a major advance; though control analysis of mitochondrial energy metabolism has been applied previously, it was limited to isolated mitochondria [17,20] and, because of the need for bulk suspensions for Clark electrode-based respirometry and radioisotope-distribution based ΔψM determinations, to suspensions of cells such as hepatocytes [18], precluding its application to adherent cells.

Using these approaches and analyses, we report two major findings. First, our data indicate a strong positive feedback loop in β-cell energy metabolism by ATP/ADP or other factors downstream of ΔψM. In other words, glucose stimulates its own metabolism, and this stimulation requires mitochondrial ATP synthesis. Second, the analysis suggests that the putative role of proton leak in regulating β-cell energetics is constrained to the fasting state of the cell, implying that physiological levels of uncoupling proteins are expected not to limit ATP/ADP at high glucose concentrations. We propose that the operation of the feedback mechanism and its defect in T2D explains recent bioenergetic findings on human primary β-cells [16] and islets [23].

2 Materials and Methods

2.1 Materials

The ΔψP indicator (PMPI; #R8042 FLIPR Membrane Potential Assay Explorer Kit) was from Molecular Devices (Sunnyvale, CA); tetramethylrhodamine methyl ester (TMRM) and Hoechst 33342 were from Life Technologies (Carlsbad, CA); zosuquidar was from MedKoo Biosciences (Chapel Hill, NC), and other fine chemicals were from Sigma-Aldrich (St. Louis, MO) or Santa Cruz Biotechnology (Dallas, TX) unless otherwise noted.

2.2 Insulinoma cell line

INS-1 832/13 cells [24] were cultured in RPMI 1640 medium containing 2 mM L-glutamine, 1 mM Na-pyruvate, 0.05 mM β-mercaptoethanol, 10 mM HEPES, and 10 v/v% fetal bovine serum. An INS-1 832/13 line stably transfected with non-targeted pSilencer 4.1 CMV-puro vector was used, and 2 μg/mL puromycin was added during cell culture and plating. INS-1 832/13 cells were plated 48–72 hours prior to the experiment in Seahorse V7 PS Flux plates and in alternating columns of Corning 3340 96-well plates (both prepared by coating with a 1:15,000 dilution of polyethylimine) at 4×10⁴ cells per well in 100 μl growth medium. For fluorescence microscopy 8-well LabTek coverglass-bottomed dishes were used, coated as described above.

2.3 Fluorescence microscopy assay of ΔψP and ΔψM

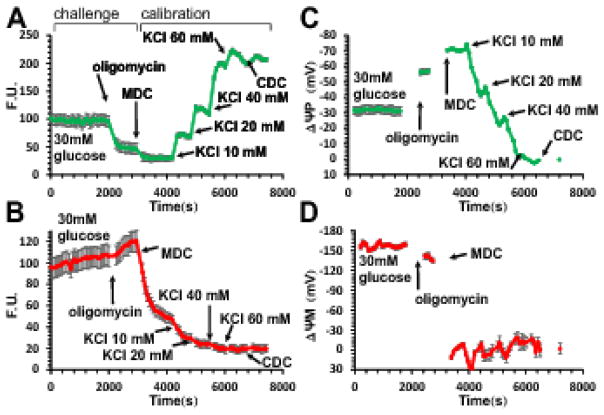
Absolute calibrated assays of ΔψP and ΔψM using wide field fluorescence microscopic time lapse imaging were performed as described in [25], in conditions similar to those described below for the microplate reader assay. The ΔψM assay is based on recording of time courses of the fluorescence of the cationic dye TMRM and an anionic bis-oxonol ΔψP indicator (PMPI). The calibration relies on a biophysical model of lipophilic potentiometric probe distribution to back-calculate potentials that cause changes in fluorescence intensities of the two probes [22]. Absolute values of potentials in millivolts are calculated from paired TMRM and PMPI fluorescence intensity values and their rates of change, using a set of calibration parameters (see Supplemental Material). The prototypical experiment in Fig. 1 was designed to allow computation of these calibration parameters, and therefore ΔψP and ΔψM, from a single fluorescence microscopy recording [22]. The calibration of ΔψP is a prerequisite for the calculation of ΔψM, because it allows separation of the effects of ΔψP and ΔψM on TMRM fluorescence and therefore calculation of ΔψM. In Fig. 1, ΔψP was calibrated by manipulation of extracellular K⁺ in the presence of the K⁺-ionophore valinomycin to ensure that the K⁺ equilibrium potential dominates ΔψP [22]. ΔψM was then calculated from the decay characteristics of TMRM fluorescence when mitochondria were completely depolarized at a maintained ΔψP. Both calibrations require fluorescence intensity measurement at 0 mV. These steps were combined in the single-run, or “complete” calibration (Fig. 1). After a recording of interest (e.g. in the presence of 30 mM glucose in Fig. 1 or a “challenge time course” in general) the mitochondrial inner membrane was depolarized using a mitochondrial depolarization cocktail (MDC; see compositions in Suppl. Table 1) triggering a characteristic decay of TMRM fluorescence intensity. Next, extracellular [K⁺] was elevated stepwise in the presence of valinomycin (a component of the MDC). The experiment was concluded by complete cellular depolarization using an ionophore cocktail (complete depolarization cocktail, CDC; See Supplemental Table 1; [22]). Fluorescence image analysis and calculations of potentials were performed using standard image processing pipelines and the “Membrane Potential Calibration Wizard” in Image Analyst MKII (Image Analyst Software, Novato, CA).

Fig. 1. Determination of absolute values of ΔψP and ΔψM in millivolts in INS-1 832/13 cells from a single time course recording using fluorescence microscopy.

(A–B) Fluorescence time courses of potentiometric probe intensities (F.U., fluorescence units). A, PMPI; B, TMRM. (C–D) Time courses of calibrated potentials corresponding to A–B calculated using parameters given in Error! Reference source not found.. Data are mean±SE of n=12 groups of cells in a single view field, representative of 7 experiments. The calibration algorithm back-calculates ΔψP from KCl-evoked depolarizations, and ΔψM from the decay of TMRM fluorescence upon a sudden and complete mitochondrial depolarization by the mitochondrial depolarization cocktail (MDC) (see Error! Reference source not found.). Both calibrations require fluorescence intensities measured at 0 mV potentials set by the complete depolarization cocktail (CDC). Note that non-quench mode TMRM fluorescence is dependent on both ΔψP and ΔψM, and a fast change in either potential (e.g. subsequent to oligomycin addition) results in a slow redistribution of the probe. The calibration algorithm deconvolutes the observed slow fluorescence change into the instantaneous potentials that cause the redistribution.

2.4 Microplate reader assay of ΔψP and ΔψM

90 min prior to experiment, growth medium was exchanged for potentiometric medium (PM) containing 120 mM NaCl, 3.5 mM KCl, 1.3 mM CaCl₂, 1 mM MgCl₂, 0.4 mM KH₂PO₄, 20 mM TES (N-Tris-(hydroxymethyl)-methyl-2-amino-ethanesulphonic acid), 5 mM NaHCO₃, 1.2 mM Na₂SO₄, 2 mM D-glucose, TMRM (10 nM), PMPI (1:200), tetraphenylborate (TPB; 1 μM) and zosuquidar (1 μM [26]). PM was made from a 2× stock (2×PM) containing all components except NaCl, and diluted to final volume using 240 mM NaCl (or 240 mM KCl, resulting in PMK). K⁺ was varied by partial replacement of PM with PMK over the specimen.

Fluorescence intensity time courses were recorded using a Pherastar FS (BMG Labtech Inc, Cary, NC) fluorescence microplate reader capable of focusing on the cell monolayer in bottom fluorescence readout mode and simultaneous detection of TMRM and PMPI fluorescence emission with a custom dual-excitation, dual-emission filter set. The filter set (Semrock, Rochester, NY) comprised a 503/572-nm dual bandpass exciter, a 444/520/590-nm multi-edge excitation beamsplitter, a 562-nm emission beamsplitter, a 537/26-nm emission filter for PMPI (custom matched to the exciter to avoid bleed through) and a 641/75-nm emission filter for TMRM. Assays were performed at 37°C under air. All media and reservoir plates were held at 37°C in an air incubator. Fluorescence measurements of the cell monolayer were optimized by focusing at the appropriate z-offset for the cell monolayer, determined as the z-offset with peak difference in fluorescence intensity between cell-containing and blank wells. Each data point was determined by orbital averaging of 20 Xe-arc flashes in 3 mm circles. Typical recordings acquired 8 full columns (64 wells) with a 36 s cycle time or 4 columns with a 19 s cycle time. Each time course consisted of sequential recordings interspersed by medium exchanges.

An experiment to determine ΔψP and ΔψM in microplates had two parts, to simplify liquid handling and allow scalability of experimental recordings. In the first part, the values of the baseline potentials (ΔψP₀ and ΔψM₀ at 2 mM glucose) were established for each cell culture plating, and this required the higher temporal resolution (Fig. 2). In the second part on separate microplates, at lower temporal resolution and higher throughput, experimental manipulations were made (the “challenge time course”; see 3.2 and Fig. 4A and B) followed by a single calibration addition. The two parts of the experiment were performed on sister cultures in separate microplates in order to keep identical incubation times in assay medium. Fluorescence time course recordings were exported to Microsoft Excel for analysis in Mathematica 8–10.2 (Wolfram Research, Champaign, IL). In Mathematica, spectral bleedthrough and fluorescence background were corrected for (Fig. 2A–B; Appendix B), and time courses of ΔψP (see Fig. 4C) and ΔψM (see Fig. 4D) were calculated using data from both parts as described below.

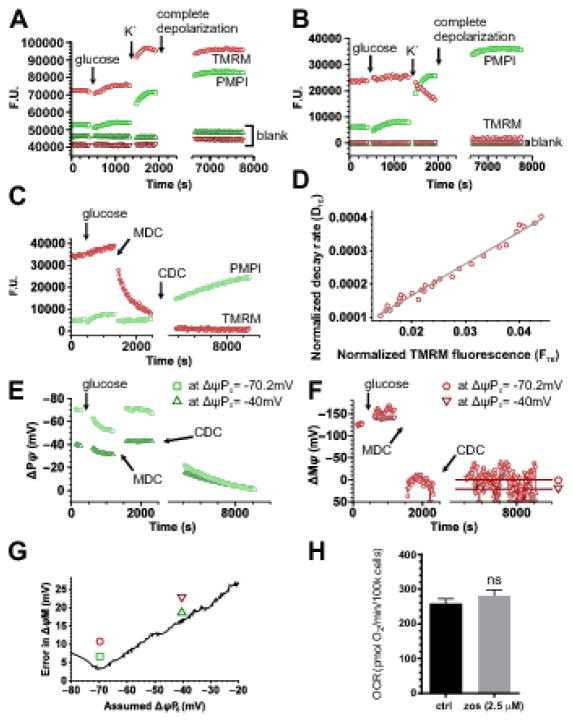
Fig. 2. Calibration of ΔψM and ΔψP using a fluorescence microplate reader.

(A–B) Spectral unmixing. (A) Unprocessed recording shown as fluorescence units in a well containing INS-1 832/13 cells and in a blank well. To demonstrate spectral crossbleed, cells were exposed to glucose (10 mM) and high extracellular [K⁺] (64 mM) increasing PMPI fluorescence and decreasing TMRM fluorescence. (B) Fluorescence intensities of the data in A after spectral unmixing (see Error! Reference source not found.) and blank well background subtraction. (C) Spectrally unmixed and background subtracted fluorescence recording for the determination of ΔψP₀, ΔψM₀ and k_T. The calibration is based on the decay of TMRM fluorescence after acute and complete mitochondrial depolarization provided by MDC, followed by complete depolarization of the cell by CDC (see compositions in Error! Reference source not found.). Data are from a representative single well chosen from 16 technical replicates in each of 10 independent experiments. (D) Linear regression analysis to calculate ΔψM₀ and k_T as described in Error! Reference source not found., corresponding to TMRM fluorescence intensities measured between MDC and CDC additions in panel C. The good linear fit indicates that the experimental system followed the biophysical model assuming a time- and ΔψP-dependent leakage of TMRM from the cytosol to the extracellular space. (E) Calibrated ΔψP and (F) calibrated ΔψM corresponding to panel C. ΔψP₀ was numerically optimized (resulting in a ΔψP time course for each iteration, see E) to give minimal deviation from 0 mV in calibrated ΔψM at the end of the recording, indicated by horizontal lines in F. Circles and squares indicate potentials calibrated at the optimum ΔψP₀, while triangles indicate those at an arbitrary different ΔψP₀ (−40 mV). (G) Dependence of the deviation of mean calibrated ΔψM from 0 mV at the end of the recording as a function of assumed ΔψP₀. Symbols correspond to panels E–F and indicate the ΔψP₀ used for the calibration of traces. (H) Zosuquidar (zos) used to prevent pumping of fluorescent probes during the assay does not alter basal respiration. INS-1 832/13 cells were preincubated in 2.5 μM zosuquidar for 90 min before cell respirometry. ns, not significant.

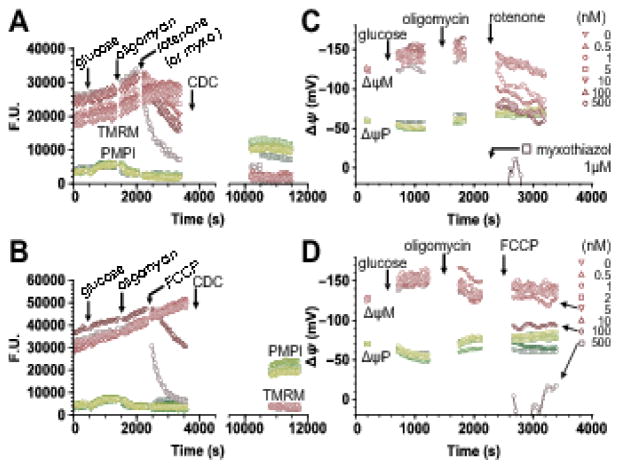
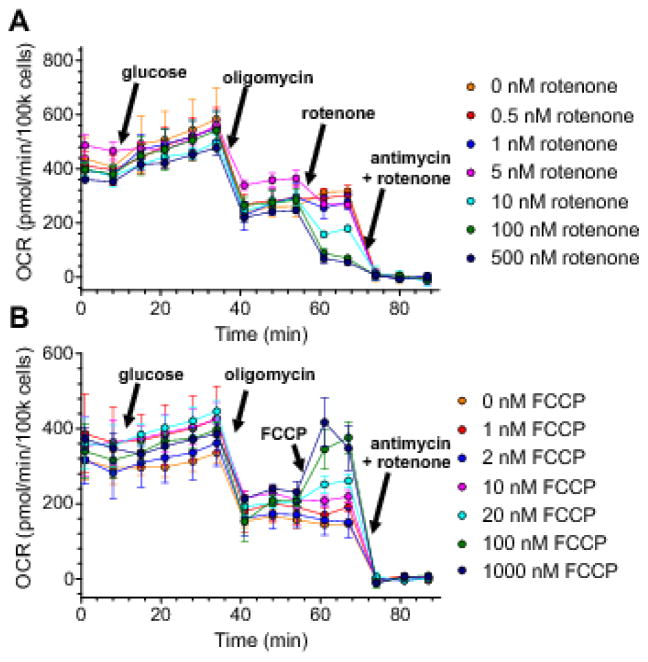
Fig. 4. Measurement of the level of the common intermediate (ΔψM) for control analysis: rotenone and FCCP titration of ΔψM in INS-1 832/13 cells.

(A,B) TMRM and PMPI fluorescence after spectral unmixing and background subtraction. Additions of glucose (10 mM final), oligomycin (2.5 μM) and rotenone (A) or FCCP (B) at concentrations indicated in panels C and D were followed by complete depolarization of both ΔψP and ΔψM using CDC. (C,D) ΔψP and ΔψM were calibrated using the “short” calibration paradigm, based on ΔψP₀, ΔψM₀ and k_T measured under identical conditions for each cell culture plating (Fig. 2; 10 platings in total), and fluorescence measured at 0 mV potential achieved at the end of the time lapse. Calibrated data points are shown only before complete depolarization. Glucose addition served to map the relationship of fluxes through the P+L modules to ΔψM by combining these data with data from Fig. 5. Oligomycin served to inhibit phosphorylation, allowing mapping of the L module by titrating glucose oxidation with rotenone (C) or mapping of the O module by titrating proton leak with FCCP (D). Traces represent single-well fluorescence or calibrated potential data from 6 (A,C) and 4 (B,D) independent experiments.

2.4.1 Determination of baseline ΔψM using microplates

The original microscopy-based assay (Fig. 1) was designed to provide calibration of both ΔψP and ΔψM following any particular experiment (“challenge time course”) using a single recording to enable measurement of membrane potentials in single cells. In applying this approach to a cell population within a microplate well, we assume that cell populations are identical between wells and microplates of the same cell culture plating prior to experimental manipulation, enabling parallelization.

ΔψM was calibrated from the decay of TMRM fluorescence after acute and complete mitochondrial depolarization by MDC, followed by complete depolarization of the cell by CDC (Fig. 2C). ΔψM₀ and the rate constant k_T were determined by transformation of these data [22] (Fig. 2D, Appendix C). k_T describes how quickly cells take up TMRM at zero ΔψP and allows calculation of ΔψM when TMRM is not in equilibrium. The calibration of ΔψP that is required to calculate ΔψM was obtained from the same data and is described later. The calculation of ΔψM₀ was subject to unbiased quality control (Appendix D). ΔψM was calculated using a mitochondria:cell volume fraction (V_F) of 6.3±0.49% (n=4) previously measured in INS-1 832/13 cells [25] and with values of V_FM=63% and a_R’=0.36±0.05 (n=3) from INS-1E cells [22]. The baseline ΔψM at 2 mM glucose and 2 mM glutamine was -118±3.9 mV (n=10). k_T was 0.012±0.001 s^-1 (n=10). This rate constant translates to 90% equilibration of TMRM in 44 min at typical ΔψP₀ and ΔψM₀ (calculated as given in [27]). Importantly, the calculation of ΔψM₀ implemented here allows for TMRM disequilibrium at baseline (see Appendix C), in contrast to our previously derived formulae [22].

2.4.2 Determination of baseline ΔψP using microplates

To simplify the experimental design, we developed an alternative ΔψP calibration using the same recording that provided ΔψM₀. This approach eliminates the requirement for [K⁺] titration or establishment of K⁺ equilibrium potentials, in contrast to the original method shown in Fig. 1. It follows from the calibration equation ([22]; Appendix A) that ΔψP can be calculated if its mV value at two calibration points is known, e.g., ΔψP₀ and 0 mV. In the new approach, ΔψP was assumed to be 0 mV at the end of the recording after complete depolarization and ΔψP₀ was obtained by numerical optimization. The optimization exploits a finding of sensitivity analysis [22] that only when an accurate ΔψP₀ is used to calculate ΔψP does the above calculation of ΔψM give 0 mV when mitochondria are completely depolarized and ΔψP has an intermediate value. To conduct the optimization, the ΔψM calibration described above was calculated for a range of assumed ΔψP₀ values spanning physiological potentials, and the ΔψP₀ value was taken as the value at which the calibrated ΔψM in completely depolarized mitochondria and partially depolarized plasma membrane was closest to zero (Fig. 2E–G). To this end the slow ΔψP-depolarizing effect of CDC was exploited, and calibrated ΔψM was averaged in the interval after CDC addition (Fig. 2F horizontal lines). Fig. 2G demonstrates that the absolute deviation of these averages from zero had a marked minimum at the expected [28] resting ΔψP of INS-1 832/13 cells. Fig. 2E–F illustrates calibrated potentials at this minimum (−70.2 mV) and at an arbitrary (−40 mV) value of ΔψP₀. The mean value of ΔψP₀ in 2 mM glucose and 2 mM glutamine obtained using this numerical optimization was −67.1±1.6 mV (n=10).

2.4.3 Calibration of ΔψM for inhibitor and uncoupler titrations

The values of ΔψP₀, ΔψM₀ and k_t determined above for INS-1 832/13 cells in the resting state (2 mM glucose) allowed the use of a simplified, “short” calibration paradigm based on the known baseline (and 0 mV) potentials in identical samples (Appendix E). Importantly, the recording for the determination of ΔψM₀ is the only time course requiring the fast data collection needed to resolve the decay characteristics of TMRM fluorescence after complete mitochondrial depolarization. This confers further experiments with scalability because only intermittent data acquisition is required to calibrate new data, and liquid handling is also minimal (one addition for the calibration). It also allows significant or complete depolarization of either or both potentials during the “challenge time course”, which would otherwise interfere or prevent single-run “complete” calibration. To perform this “short” calibration, experiments started with the resting state followed by a “challenge time course” and were finished by complete depolarization. This approach also accommodates differences in cell number in each well, because all intensity-related calibration parameters are calculated for each well. Parameters that describe the cell line at resting state (ΔψP₀, ΔψM₀, k_t) were used from preceding recordings on sister cultures. Importantly, recording on sister cultures is not a strict requirement and once these values are established for the particular cell line and basal condition they can be reused for the subsequent experiments. In support, performing calibrations with individual ΔψP₀, ΔψM₀, k_t values for each plating or using a single mean value obtained from all experiments did not result in a significant difference in millivolt values (e.g. −141 ± 4.1 mV vs −146 ± 2.5 mV, respectively, n=10 in the presence of 10mM glucose; see 3.2).

2.5 Cell respiration

Oxygen consumption rates (OCR) were measured using a Seahorse XF24 Extracellular Flux Analyzer (Seahorse Bioscience, Billerica, MA). After 48–72 h growth and 90 min prior to experiment, growth medium was exchanged for PM lacking PMPI but otherwise identical to the conditions of the microplate reader assay, including TMRM, TPB, and zosuquidar. Zosuquidar did not affect oxygen consumption rates (Fig. 2H). Respiration was measured as described [29]. Briefly, it was measured in cells at 2 mM glucose and 2 mM glutamine (resting state), followed by sequential additions of glucose to 10 mM (activated state) and 2.5 μM oligomycin (non-phosphorylating state). Then, depending on the module tested, 0.5–500 nM rotenone, 1 μM myxothiazol or 1–1000 nM FCCP was added. Respirometry was concluded by application of 2 μM antimycin plus 2 μM rotenone to determine non-mitochondrial respiration (which was subtracted from all other values). Immediately following respirometry, cells were fixed for 30 min in 4% (w/v) formaldehyde, and nuclei were stained with 2 μg/mL Hoechst 33342 for 15 min. Cells were imaged using a Nikon Ti-Eclipse Perfect Focus System and nuclei were counted in the acquired images using the “Whole Well Cell Count” standard pipeline in Image Analyst MKII.

2.6 Metabolic control analysis

Elasticities and control coefficients were calculated as in [17], response coefficients were calculated as in [18,30] and these formulae are also given in Appendix F. Elasticities measure the fractional change in steady-state flux through a module in response to an infinitesimal fractional change in the concentration of an intermediate (here, ΔψM). We assumed that the population of glucose-stimulated cells was at steady state (even though certain variables oscillate in individual cells [31]), because ΔψM remains relatively steady in 832/13 cells [31] and in most primary β-cells in dispersed culture [16,25]. We also assumed that known β-cell heterogeneity [25,32] does not invalidate the method. For practical reasons, elasticities to $\mathrm{\Delta }\mathrm{\psi }\mathrm{M}({{}^{\ast }\epsilon }_{\mathrm{\Delta }\psi M}^i)$ of each module (glucose oxidation (i = O), proton leak (i = L) and phosphorylation plus ATP turnover (i = P)) were determined as the slopes of lines fitting all or connecting a pair of key measured data points in double-logarithmic plots of respiration versus ΔψM. We assumed that elasticities vary little with locally changing ΔψM, allowing their calculation from large changes rather than infinitesimal ones. Possible errors due to violations of this assumption are discussed below. All other coefficients were expressed using these elasticities, fluxes (J_i, where i is O, L or P), and ΔψM, at 2 mM and 10 mM glucose. J_P was calculated as the difference between the uninhibited flux (J_O) and J_L. To this end J_L was calculated at the required ΔψM by interpolation using the above linear fit. Concentration control coefficients ( ${{}^{\ast }C}_i^{\mathrm{\Delta }\psi M}$), the fractional change in ΔψM upon a change in the activity of module i, and flux control coefficients ( ${{}^{\ast }C}_i^{J_j}$), the fractional change in the flux through module j upon a change in the activity of module i, were calculated using equations 1–12 in [17]. Partial internal response coefficients of ΔψM to a change in ΔψM acting through flux changes through module $i({{}^{i}R}_{\mathrm{\Delta }\psi M}^{\mathrm{\Delta }\psi M})$ were calculated using equation 6 in [18]. Partial integrated responses of ΔψM to a step change in [glucose], acting through changes in the activity of module $i({}^{i}I{R}_{\mathrm{\Delta }\mathit{glucose}}^{\mathrm{\Delta }\psi M})$ were calculated using equations 4 and 7 in [18], and were normalized to 100%. These values express how strongly each module mediates a glucose-induced change in ΔψM by a change in its activity.

2.7 Data and statistical analysis

Potentiometric calibration, metabolic control analysis and statistical analysis were performed in Mathematica 8.0–10.2. The standard error (SE) of the mean of independent experiments is reported, and these measurement errors were propagated to the SE of all derived values. The SE for elasticities was calculated using the LinearModelFit standard function in Mathematica as the estimated SE of the slope of the fit line. The fit was weighted with the reciprocal of squared measurement errors, and the SE of the slope and mean prediction were calculated from these measurement errors instead of residuals. The squared measurement errors were expressed as the square sum of the SE of respiration rate and the propagated error of ΔψM. The SE of the mean prediction was used to indicate the confidence of the fit at 1 SE in Fig. 6B, and to estimate the SE of the flux at an arbitrary ΔψM. Control and response coefficients were expressed by elasticities, fluxes and levels to derive error propagation formulae and their SEs were calculated by substituting measured means and SEs. For statistical comparison of control or response coefficients described by a mean value and propagated SE two-tailed Welch t-test was used taking n as the mean of independent experimental repeats. This analytical approach gave similar albeit smaller SEs than performing Monte-Carlo simulation [33], and the statistical distributions of control coefficients obtained by simulated experiments were close to normal distributions (not shown), likely due to the relative simplicity of the single intermediate system. Therefore we chose to use error propagation and parametric statistical testing over Monte-Carlo simulation.

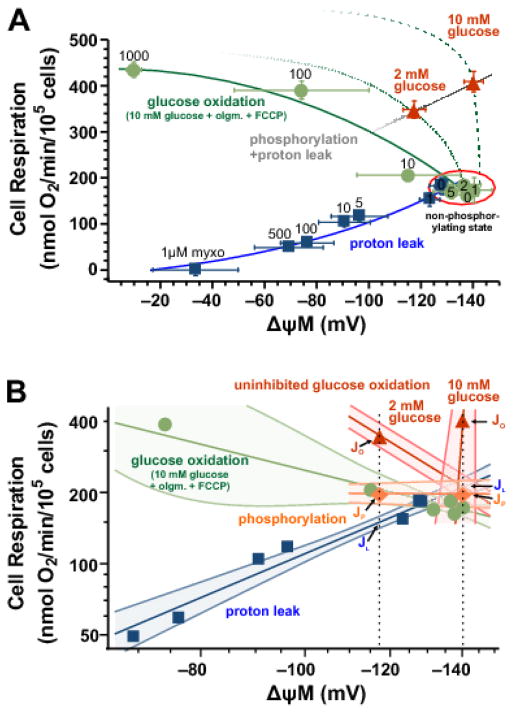
Fig. 6. Modular kinetic analysis of energy metabolism in INS-1 832/13 cells.

(A) Kinetic analysis of the response of the proton leak (blue squares; bare labels above or over symbols indicate nM concentration of rotenone), oligomycin-inhibited glucose oxidation (green circles; labels above or over symbols indicate nM concentration of FCCP) and phosphorylation plus leak (red triangles) modules to ΔψM was compiled from ΔψM data in Fig. 4 and respiration data in Fig. 5. Only data from matching concentrations were used from these two assays. Red triangles indicate the uninhibited resting and activated states corresponding to low (2 mM) and high (10 mM) glucose, respectively. The red ellipse indicates the non-phosphorylating state in the presence of 10 mM glucose and oligomycin (2.5 μM). The leak curve (blue line) was mapped by rotenone titration, while the glucose oxidation curve (solid green line) was mapped by FCCP titration, starting from the point representing the non-phosphorylating state. The phosphorylation plus proton leak curve is mapped by the uninhibited points at 2 mM and 10 mM glucose (gray line). Kinetic curves are not fits and are for illustration only, see panel B for quantitative analysis. Dotted and dashed green curves illustrate probable uninhibited glucose oxidation kinetics, based on the available two data points and comparable literature [20,42]. Data are mean±SE of n=(10,14) for points representing the uninhibited and non-phosphorylating states, n=(6,9) for proton leak and n=(4,3) for glucose oxidation, where n is expressed as (ΔψM, respiration) independent experiments. (B) Log-log conversion of the data shown in panel A with the addition of phosphorylation fluxes (J_P; orange diamonds and line) calculated by subtraction of proton leak fluxes (J_L; interpolated and extrapolated to the required ΔψM marked by the black dotted vertical lines) from uninhibited fluxes (J_O. Lines are weighted linear fits for proton leak and oligomycin-inhibited glucose oxidation, or connecting lines of available pairs of data points for other modules, including the uninhibited glucose oxidation module for 2 and 10 mM glucose separately (red lines). The confidence bands around fit lines indicate ±1 SE. Symbols correspond to panel A with error bars omitted here. olgm, oligomycin; myxo, myxothiazol.

3 Results

3.1 Metabolic control analysis of INS-1 832/13 cell energy metabolism

Complicated metabolic networks can be simplified to modules, or blocks of reactions, connected by small numbers of defined intermediates. This makes them tractable for systems analysis, which can reveal important information about the emergent behavior of the network. The modularization requires independent blocks of reactions linked only by common intermediates, but is otherwise arbitrary. To analyze cellular energy metabolism, we defined protonmotive force across the mitochondrial inner membrane as the common intermediate linking supply and demand pathways. Since protonmotive force is well-represented under most conditions by ΔψM, we measured ΔψM in our analysis. Three modules are connected by ΔψM: glucose oxidation (including glycolysis, the pentose phosphate pathway, the tricarboxylic acid cycle and the respiratory chain; O), phosphorylation (ATP synthesis and cellular ATP consumption; P), and proton leak (L) (Fig. 3). The overall flux through the system is reported by the rate of electron flow through the respiratory chain, and can therefore be measured as mitochondrial respiration. The fluxes through the demand modules can be expressed as respiration driving phosphorylation and respiration driving proton leak. Using micro-scale assays for respiration rate and ΔψM, we determine below how the steady-state flux through each module changes as a function of the common intermediate, ΔψM, when this is altered by pharmacological modulation of other modules while the queried module remains uninhibited. These data are then used in the calculation of the modular kinetic properties of cellular energy metabolism, control analysis quantifying how β-cells regulate and stabilize fluxes and ΔψM, and regulation analysis quantifying responses to changes in glucose concentration. Notably, we look at β-cell energy metabolism in isolation here, and relate ΔψM to insulin secretion only by considering the canonical pathway of GSIS. While stimulation of insulin secretion by glucose in these cells is well characterized [24,34–36], the experimental conditions needed to interrogate the control of cellular energy metabolism prevent insulin secretion because of inhibition of mitochondrial ATP synthesis, and therefore secretion was not monitored.

Fig. 3. Modularization of energy metabolism.

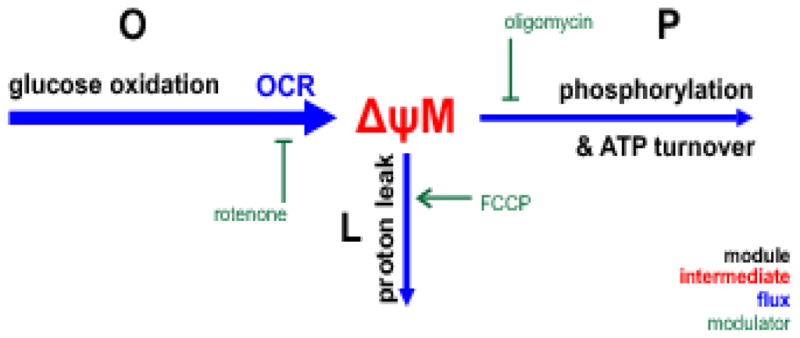
Energy metabolism was partitioned into thee modules (black labels): glucose oxidation, O (including glucose uptake, glycolysis, tricarboxylic acid cycle and the respiratory chain), proton leak, L and phosphorylation, P (ATP synthesis and the use of ATP by the cell). These modules share a common intermediate, ΔψM, and there are different fluxes through each (blue arrows; weight indicates the magnitude of the flux). The flux supplying ΔψM is the pumping of protons out of the mitochondrial matrix by the respiratory chain. Since a fixed number of protons is pumped per oxygen consumed, this is measured as mitochondrial oxygen consumption rate of the cells. The protons can reenter the matrix through proton leak or to drive phosphorylation of ADP; the sum of these two fluxes equals the flux of proton pumping. Therefore these fluxes can be expressed as the respiration rate required to drive them. Modulators of each module are shown in green. OCR, oxygen consumption rate.

3.2 Inhibitor and uncoupler titrations of ΔψM in INS-1 832/13 cells

To measure steady state levels of ΔψM, a simplified paradigm of the absolute potentiometric calibration [22,25] was developed and used (see 2.4.3). Fig. 4A and B show background-subtracted and spectrally-unmixed fluorescence data recorded using this paradigm, and Fig. 4C and D show the corresponding calibrated potentials. All recordings started identically, with a 90 min fasting period in potentiometric medium containing 2 mM glucose and 2 mM glutamine. Recording of the initial steady state in 2 mM glucose (baseline) was followed by addition of glucose to 10 mM. This caused ΔψM to hyperpolarize from −118 ± 3.9 mV to −141 ± 4.1 mV in 10 min (n = 10; Fig. 4B and D). To interrogate the L module in this glucose-stimulated condition (see Fig. 3), the P module was completely inhibited by oligomycin (an inhibitor of the ATP synthase), and the remaining module, O, was inhibited to different extents in different wells by different concentrations of rotenone to decrease ΔψM (Fig. 4A,C). Notably, rotenone, and not other inhibitors was used here because of its stabile, titratable effects. The addition of oligomycin caused no significant change in ΔψM. To completely inhibit the respiratory chain, myxothiazol (a complex III inhibitor; 1 μM) was used. Separately, to interrogate the O module, different concentrations of FCCP (an uncoupler; 1–200 nM) were used after oligomycin addition in a similar paradigm (Fig. 4B,D). As expected, both respiratory inhibition and uncoupling decreased ΔψM. The P module was not directly interrogated in a separate experiment, but is described as P+L modules by the 2 mM and 10 mM glucose data points, where the O module was activated by elevation of glucose concentration.

3.3 Inhibitor and uncoupler titrations of mitochondrial respiration in INS-1 832/13 cells

Mitochondrial respiration rate was determined under nearly identical conditions as ΔψM, with interrogation of the L and O modules exactly as described above (Fig. 5). Respiration rate was normalized to cell counts performed after respirometry by fluorescence imaging of the entire bottom of the wells. The baseline recording was followed by addition of 10 mM glucose (Fig. 5), causing a gradual increase in respiration. Oligomycin caused a drop in respiration rate to the rate driving proton leak (non-phosphorylating state). This rate was further decreased by titration with rotenone (Fig. 5A) or increased by titration with FCCP (Fig. 5B).

Fig. 5. Measurement of the fluxes through the system for control analysis: rotenone and FCCP titration of respiration of INS-1 832/13 cells.

(A,B) Respiration of INS-1 832/13 cells cultured in identical conditions to Fig. 2 and Fig. 4, but in Seahorse V7 PS flux plates. Additions of glucose (10 mM), oligomycin (2.5 μM) and the indicated concentrations of rotenone (A) or FCCP (B) were followed by rotenone (2 μM) plus antimycin A (2 μM) to determine non-mitochondrial respiration (which was subtracted from all data). Oxygen consumption rate (OCR) is shown normalized to whole-well cell numbers counted after respirometry. Glucose addition served to map the relationship of fluxes through the P+L modules to ΔψM by combining these data with data from Fig. 4. Oligomycin served to inhibit phosphorylation, allowing mapping of the L module by titrating glucose oxidation with rotenone (A) or mapping of the O module by titrating proton leak with FCCP (B). Data are mean±SE of (A) n=9 and (B) n=3 experiments.

3.4 Modular kinetic analysis of β-cell energy metabolism

β-Cell metabolism is specialized to allow sensitive responses of insulin secretion to changed extracellular glucose levels. We ask here how bioenergetic supply and demand interact to allow ΔψM, and therefore downstream ATP/ADP and insulin secretion, to respond sensitively to glucose level. To describe and quantify how the interaction of the three modules depicted by Fig. 3 achieves this, we first conducted a modular kinetic analysis by combining all the data collected above as a force-flux diagram showing respiration rate (the flux) as a function of ΔψM (the force) (Fig. 6A).

3.4.1 Proton leak module

Starting at the non-phosphorylating state in the presence of oligomycin (red ellipse; 10 mM glucose), as the respiratory chain (O module) was progressively inhibited by increasing concentrations of rotenone (a complex I inhibitor), both respiration rate and ΔψM decreased (Fig. 6A, blue squares). Because phosphorylation was inhibited by oligomycin, and respiration rate therefore reported only proton leak rate, these data points describe the dependence of proton leak rate on ΔψM, i.e. the activity of the L module, or the “leak curve” (Fig. 6A, blue line). An increase in proton leak activity (e.g. expression of uncoupling proteins or addition of the uncoupler FCCP) would shift this curve upwards [37].

3.4.2 Glucose oxidation module

Starting at the non-phosphorylating state (red ellipse; 10 mM glucose with oligomycin), as ΔψM demand was progressively increased by increasing FCCP, respiration rate increased and ΔψM decreased as expected (Fig. 6A, green solid circles). These data points outline the kinetic dependence of glucose oxidation on ΔψM, i.e. the activity of the O module, or the “glucose oxidation curve” (Fig. 6A, green line). Activation of glucose oxidation (e.g. addition of higher concentrations of extracellular glucose, increased activity of glycolysis, pyruvate transport, tricarboxylic acid cycle or respiratory chain) would shift the glucose oxidation curve upwards, to reflect higher flux at each ΔψM [37].

3.4.3 Phosphorylation module

Starting at the uninhibited resting state (Fig. 6A 2 mM glucose red triangle) respiration and ΔψM were increased by increasing glucose to 10 mM (10 mM glucose red triangle). These two data points outline the kinetic dependence of the P + L modules on ΔψM. Knowing the “leak curve”, the kinetic dependence of the P module on ΔψM is calculated by subtraction.

3.5 Energization-dependent positive feedback to glucose oxidation

Fig. 6B is a log-log representation of the force-flux diagram in Fig. 6A, and this transformation allowed us to approximate kinetic curves with linear fits, and to estimate the uncertainty of calculated values. Remarkably, the data points at 2 and 10 mM glucose with no inhibitors (Fig. 6B, red triangles) did not lie on the glucose oxidation curve (green line and solid circles), which was also measured in 10 mM glucose, but with the P module compromised by oligomycin, but lay significantly above it (p<0.001). The significance was tested by calculating fluxes in the L module at identical ΔψM to the 2 and 10 mM glucose data points (dotted vertical lines in Fig. 6B). This difference indicates inhibition of the O module in the presence of oligomycin. Importantly, this effect of oligomycin was not simply due to an inhibition of demand (because demand does not contribute to the shape of the glucose oxidation curve, only to the position of the points along it), but is the signature of a decreased activity of the O module. The difference in the kinetics of the O module between the two 10 mM glucose conditions is caused by the specific effect of oligomycin on the internal workings of the P module. In the absence of oligomycin, ATP synthesis will allow ATP/ADP and other internal intermediates of the P module to be closely coupled to ΔψM. However, in the presence of oligomycin ATP/ADP will fall due to inhibited ATP synthesis, and no longer be strongly coupled to ΔψM. These data show that β-cell energization increases the response of glucose oxidation to ΔψM, and therefore indicates the operation of a positive feedback loop between ATP/ADP (or other downstream signals such as Ca²⁺) and control-bearing components of the glucose oxidation module (such as glucokinase [38,39] and/or phosphofructokinase [40]). We can tell that the feedback is from a component of the P module such as the ATP/ADP ratio, because it is prevented by addition of oligomycin (Fig. 6A), which decouples the downstream elements from changes in ΔψM. Crucially, this positive feedback causes a very steep response of glucose oxidation to ΔψM near the non-phosphorylating state (Fig. 6A, approximated by the green dashed line).

3.6 Metabolic control analysis of oxidative phosphorylation in INS-1 832/13 cells

To measure the control exerted by the O, L and P modules over the different system fluxes, and to quantify the relative importance of O, L and P modules in determining the value of ΔψM, we performed metabolic control analysis in low and high glucose using the data shown in Fig. 6. To quantify the response of β-cell metabolism to changes in glucose concentration and to determine how that change propagates through the metabolic system, we also applied a subset of metabolic control analysis, regulation analysis [19], which “decodes” underlying activity changes (changes in amounts or activation status of enzymes or modules) that drive changes in fluxes and intermediate levels as external conditions (such as glucose concentration) change.

The three-branched system (Fig. 3) is validly described by the mathematical formalism of metabolic control analysis only if ΔψM is the sole intermediate between the modules. If other interactions exist through intermediates not made explicit in the system (e.g. ATP/ADP ratio), they must be related to ΔψM by some unique function [41]. The kinetic analysis in Fig. 6 revealed the operation of a positive feedback mechanism from the P module to the O module. Importantly, this does not invalidate the analysis below. The L curve is valid, because proton leak does not depend on bioenergetic intermediates other than ΔψM. The 2 and 10 mM glucose data points are acceptable points on the glucose oxidation curves, because the feedback interaction between P and O modules is included in the kinetic response of module O to ΔψM. This is because the feedback is mediated by ATP/ADP or another downstream effector whose level is assumed to be a unique function of ΔψM. In contrast, oligomycin breaks this linkage between ΔψM and feedback by inhibiting downstream ATP synthesis, invalidating the O curve obtained by FCCP titration in the presence of oligomycin, which was excluded from analysis of conditions lacking oligomycin. Finally, we assume that the non-phosphorylating state point itself is valid, because effects of the feedback loop are expected to be minimal when the glucose oxidation flux is small. Further assumptions related to the applicability of metabolic control analysis are given in the Methods and addressed in the Discussion.

3.7 Control analysis (control coefficients): the control structure of β-cell energy metabolism at low and high glucose

Elasticities quantify the change in flux through a module when the intermediate (ΔψM) changes by a small amount in the absence of any other changes in the system. Because elasticities are always normalized to the starting values, it is convenient to measure them as the slopes of linear fits in log-log plots of the force-flux relationships (Fig. 6B). A larger (positive or negative) elasticity means that the flux through a module is very sensitive to ΔψM, and is indicated by a steeper slope in the corresponding line in the force-flux diagram (Fig. 6A–B). An important aspect of the analysis given below is that the limited number of data points describing individual modules (Fig. 6) is sufficient to calculate all required elasticities without committing large errors, using a set of rational assumptions (see 4.1.5). The values of the elasticities for the system described in Fig. 3 and measured in Fig. 6B are given in Table 1.

Table 1.

Metabolic control analysis of energy metabolism in INS-1 832/13 cells.

i =		O	L	P
	Glucose concentration (mM)	glucose oxidation	proton leak	phosphorylation
elasticities
${{}^{\ast }\epsilon }_{\mathrm{\Delta }\psi M}^i$	2	−2.8±1	1.9±0.37	−0.016±0.92
	10	62±280
concentration control coefficients (fractions expressed as percent)
${{}^{\ast }C}_i^{\mathrm{\Delta }\psi M}$	2	28±8.6%	−12±3.8%	−16±5.2%
	10	−1.6±7.4%*	0.85±3.8%*	0.79±3.6%*
flux control coefficients (percent of total control)
${{}^{\ast }C}_i^{J_O}$	2	23±13%	33±6%	44±8.9%
	10	−1.6±7.3%	52±5.7%*	49±7.7%
${{}^{\ast }C}_i^{J_L}$	2	53±18%	77±7.9%	−30±11%
	10	−3.1±14%*	102±7.4%*	1.5±6.9%*
${{}^{\ast }C}_i^{J_P}$	2	−0.44±25%	0.19±11%	100±14%
	10	0.03±1.5%	−0.01±0.78%	100±0.73%
partial internal response coefficients for homeostasis of ΔψM (percent of total control)
${{}^{i}R}_{\mathrm{\Delta }\psi M}^{\mathrm{\Delta }\psi M}$	2	−77±13%	−23±7.9%	0.25±14%
	10	−102±7.3%	1.6±7.4%*	−0.01±0.73%
partial integrated response of ΔψM to glucose (percent of total response)
${}^{i}I{R}_{\mathrm{\Delta }\mathit{glucose}}^{\mathrm{\Delta }\psi M}$	2 to 10	102±29%	−2±10%	−0.02±19%
	10 to 2	100±24%	−0.1±0.8%	−0.00±1.1%

Data are means±SE. Errors were calculated by error propagation for an average of 7.7 independent experimental repeats (n averaged between respirometry and ΔψM assays).

^*p<0.05 by Welch t-test comparing conditions with 2 and 10 mM glucose for each coefficient.

The distribution of control within any system can be fully quantified from its structure and the elasticities and fluxes. Concentration control coefficients were calculated from elasticities and fluxes as described in Methods to express how a change in the activity of each module affects ΔψM [17]. By definition, the concentration control coefficients of supply and demand are equal and opposite. Table 1 shows that at 2 mM glucose control of ΔψM is strong, whereas at 10 mM glucose it is an order of magnitude weaker, reflecting the great sensitivity of ΔψM (and downstream insulin secretion) to effectors at low glucose, but its stability at high glucose. In other words, ΔψM responds to activation or inhibition of supply or demand pathways more in low glucose and less in high glucose. Within the demand modules, Table 1 shows that control of ΔψM was shared about equally between L and P at both low and high glucose, similar to results from isolated INS-1E mitochondria [42]. This shows that while proton leak may be a significant regulator of ΔψM in the fasting condition, it only weakly controls ΔψM at high glucose, just like the other modules.

Flux control coefficients were also calculated from the elasticities and fluxes to express how a change in the activity of each module affects the flux through each module [17]. At 2 mM glucose control of respiration rate ( ${{}^{\ast }C}_i^{J_O}$) was well-distributed between the three modules, but at 10 mM glucose the O module lost control to the other modules ( Table 1), as expected.

The control of a module by its own activity [18] is of particular interest, because a small flux “self”-control coefficient (e.g. ${{}^{\ast }C}_O^{J_O}$) is caused by a large elasticity to the intermediate compared to the elasticities of other modules in the system. In other words, respiration associated with the module is relatively strongly determined by ΔψM. In contrast, a value close to 100% indicates that its elasticities are relatively small and the flux through the module is governed mostly by its own activity, and less by ΔψM. Glucose oxidation had very little control over its own flux. This suggests that the layout of cellular energy metabolism in INS-1 832/13 cells confers a strong sensitivity to glucose by making glucose oxidation very insensitive to changes in enzymatic activities within this module, other than the ΔψM-linked effects of the feedback loop discovered above. In contrast, the leak module displayed strong “self”-control ( ${{}^{\ast }C}_L^{J_L}$) and also controlled phosphorylation to a small extent at 2 mM glucose but not at 10 mM glucose. The P module was highly controlled by its own activity, indicating that major ATP consumers are little affected by changing energization between 2 and 10 mM glucose.

3.8 Control analysis (partial internal response coefficients): homeostatic control of ΔψM in β-cells at low and high glucose

Since glucose-stimulated insulin secretion uses ATP levels rather than the flux of phosphorylation as an intermediate signal, a goal of this study was to determine how homeostasis of ΔψM, which is linked to ATP/ADP, is mediated by the interplay of the three modules. This is further emphasized by our findings above, that the flux of phosphorylation is largely controlled by its own activity changes, but not by glucose oxidation, and J_P did not change between 2 and 10 mM glucose.

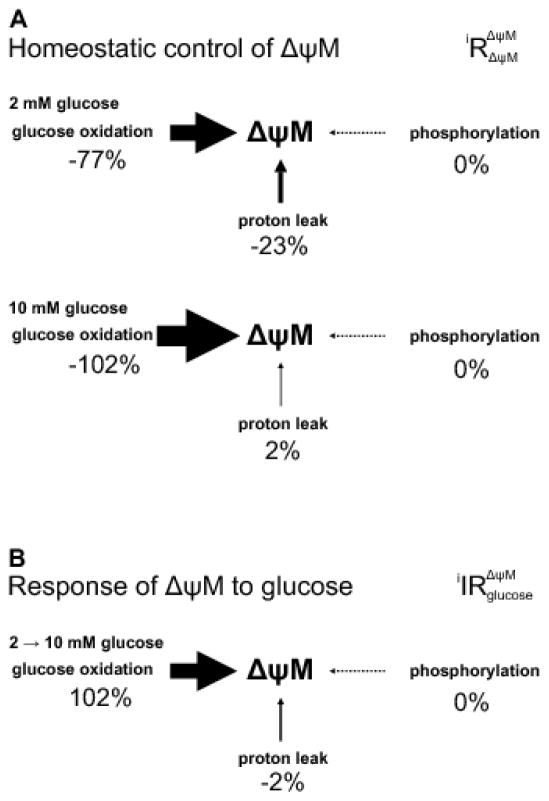
The concentration control coefficients calculated above quantify the fractional change in ΔψM in response to a change in the activity of each module. In contrast, homeostatic control describes how strongly each module maintains the steady state level of the intermediate when activities do not change. Any increase in an intermediate (e.g. caused by random fluctuations) will increase its consumption and decrease its production due to mass action effects until the steady state is regained, and the magnitude of this effect may be distributed differently between supply and demand modules. Here we assess how much the rate through each module changes if ΔψM is perturbed, to re-establish the steady state. This homeostatic response is quantified by the partial internal response coefficients [18] (Fig. 7A, Table 1). At 2 mM glucose, glucose oxidation had higher homeostatic control over ΔψM (77% of the total) than the L module (23%) while the P module had none. At 10 mM glucose essentially all of the homeostasis of ΔψM shifted to glucose oxidation. Therefore, although proton leak is generally high in INS-1 832/13 cells [42,43], its homeostatic control over ΔψM is substantial only at low glucose, and close to zero at high glucose. Thus, cellular ATP turnover and proton leak play little role in stabilizing steady state ΔψM at high glucose.

Fig. 7. Homeostatic control and response of ΔψM to glucose.

(A) Homeostatic control of ΔψM is quantified by partial internal response coefficients of ΔψM to a change in ΔψM acting through each indicated module. Values are shown as percent of total (their sum is therefore 100% for the system) separately for 2 and 10 mM glucose conditions. The size of arrows is proportional to the strength of control. Data correspond to Table 1, see errors there. (B) The contribution of the three modules to bringing about glucose-induced changes in ΔψM is quantified by the partial integrated responses of ΔψM to the change in [glucose] acting through direct effects of glucose on each module. These responses were calculated as fractional changes in ΔψM, and normalized to total 100% for better visualization.

3.9 Regulation analysis: the response of ΔψM to glucose in β-cells

Finally, we sought the contribution of the three modules in bringing about the observed hyperpolarization of ΔψM due to a change in their activities when glucose is raised from 2 to 10 mM. To this end the partial integrated responses ( ${}^{i}I{R}_{\mathrm{\Delta }\mathit{glucose}}^{\mathrm{\Delta }\psi M}$) of ΔψM to the change in [glucose] acting through the direct effects of glucose on each module (i) were calculated [30]. The calculation uses the elasticities and concentration control coefficients of the system in its initial state, and the fractional changes in fluxes and ΔψM caused by moving the system into a new steady state by adding (or removing) glucose. We calculated the partial integrated responses using both 2 and 10 mM glucose as the initial state, with virtually identical results ( Table 1). These data show that the glucose-stimulated increase in O module activity (that implicitly includes the effect of glucose as a substrate), rather than any changes in the activities of the P and L modules, causes the observed hyperpolarization of ΔψM (Fig. 7B). In other words, increased metabolism of glucose and not inhibition of futile cycling in glycolysis or altered ATP demand mediates hyperpolarization of ΔψM upon an increase in glucose concentration.

4 Discussion

4.1.1 Homeostasis, modular kinetic analysis, control analysis and regulation analysis in insulinoma cells

Homeostasis occurs when the concentration of a metabolite is kept constant despite changes in the fluxes through the system [19]. Cellular energization, ATP/ADP, and mitochondrial protonmotive force are subject to strict homeostatic regulation in many tissues, e.g. liver [44] and heart [45]. Critically, plasma glucose homeostasis is achieved through alterations in insulin levels by a metabolically exceptional cell type (pancreatic β-cells) in which the programmed lack of homeostasis of cellular energization state allows the signaling machinery of insulin secretion to sense and respond to changes in blood glucose concentration. This signaling machinery is dysfunctional in diabetes (type 2 and pre-type 1) [8–14], making the understanding of β-cell bioenergetic function and dysfunction vital for understanding and treating diabetes. In T2D, ΔψM in β-cells becomes less sensitive to changes in blood glucose [16,46–48] by unknown mechanisms.

Here we divided pancreatic insulinoma cell energetics into three all-inclusive, simplified modules connected by a single common intermediate, ΔψM. We analyzed its control and regulation using the powerful tools of metabolic control analysis to understand how the cellular metabolic network is poised to change ΔψM (and ATP/ADP) in response to changes in glucose concentration. We show that the control properties can readily be measured in adherent insulinoma cells in a microplate reader format using standard cell respirometry, parallel to the microplate-based quantitative assays of ΔψM introduced here. Modular kinetic analysis revealed the presence of a strong feedback control over glucose oxidation from downstream elements of the phosphorylation module. This feedback loop greatly enhances the response of ΔψM to glucose addition, making it an important player in GSIS. Control analysis showed that proton leak contributes to the control over the magnitude and the homeostasis of ΔψM at low glucose but not at high glucose concentrations, revealing a possible regulatory role of proton leak that is confined to the low-glucose state.

4.1.2 Relationship of results with insulinoma cells to primary human β-cells and T2D

Control over energy metabolism in INS-1 832/13 cells reflects several observations made in nondiabetic human β-cells, making these insulinoma cells a relevant model system that is well-suited to the analysis described here. These observations include the large range of ΔψM between low and high glucose, and the insensitivity of ΔψM to oligomycin at high glucose concentrations [16]. As demonstrated by the kinetic analysis performed here, this insensitivity to oligomycin reflects a very steep response of glucose oxidation to ΔψM, supported by a positive feedback from the P-module. In turn, the shape of the glucose oxidation curve is critical to achieve high ΔψM (and ultimately, insulin secretion) at high extracellular glucose concentration (Fig. 6). The kinetic and control analyses provide insight into two important observations on the glucose response of ΔψM in primary human pancreatic β-cells from T2D individuals [16].

Firstly, while normal β-cells showed no oligomycin-evoked ΔψM hyperpolarization in high glucose, T2D β-cells showed a substantial ΔψM hyperpolarization. Although respiration data are not available, the ΔψM responses to oligomycin suggest that the glucose oxidation curve at high glucose must be very steep in normal human primary β-cells, as it is in insulinoma cells (Fig. 6, dashed green line), and shallower in T2D, therefore ${{}^{\ast }\epsilon }_{\mathrm{\Delta }\psi M}^O$ must be significantly smaller in diabetic than in normal human β-cells. Notably, basal and glucose-induced respiration rates are also decreased in T2D islets [23], consistent with the shallower response to ΔψM, and suggest no increase in proton leak or ATP turnover. These considerations raise the possibility that a deficit in the glucose-induced kinetic activation of glucose oxidation is a potential cause of impaired glucose-evoked ΔψM hyperpolarization observed in T2D. This is because the steady state of ΔψM formed at the intersection of the glucose oxidation and P+L curves shifts to the left (to smaller ΔψM) when the former becomes shallower (Fig. 6A).

Secondly, we found previously that in normal β-cells, but not in T2D β-cells, ΔψM decreased when downstream pathways of GSIS were activated in low glucose by glibenclamide, an inhibitor of K_ATP channels [16]. The depolarization in normal β-cells may be explained as an effect of glibenclamide-induced ATP turnover, and the lack of it by a smaller activity-induced ATP turnover in T2D, even though the evoked ΔψP depolarization was identical between T2D and normal β-cells [16]. Alternatively, the glibenclamide-induced ΔψM depolarization in normal β-cells is predictable by the above kinetic analysis scheme if the glucose oxidation curve becomes shallower in the presence of glibenclamide. This may happen if ATP/ADP decreases because the glibenclamide-induced ATP turnover is not matched by increased supply, and this deenergization reduces the amount of positive feedback on glucose oxidation. Importantly, in INS-1 832/13 cells, the activity of glucose oxidation was lower when in was compromised by oligomycin plus FCCP in 10 mM glucose than in 2 mM glucose without inhibition. This suggests that the positive feedback loop is partially active at 2 mM glucose, and the glucose oxidation curve can get shallower during deenergization. This mechanism assumes that the feedback is through ATP/ADP and not other downstream factors, such as Ca²⁺, that reach high levels in the presence of glibenclamide. With these assumptions, we propose that both the oligomycin-induced ΔψM hyperpolarization at high glucose and the lack of glibenclamide-induced ΔψM depolarization in low glucose observed in T2D β-cells [16] can be ascribed to a defect in an ATP/ADP-dependent positive feedback mechanism in T2D.

4.1.3 Inhibition of mitochondrial ATP synthesis limits substrate supply to mitochondria

Prior studies reported failure of cell respiration when ATP synthase was inhibited in cells. Cell respiration in oligomycin-inhibited INS-1E (but not HEK293) cells gradually declined due to unidentified effects on substrate supply to the respiratory chain [49]. ATP synthase inhibition was also found to reduce maximal uncoupled respiration in certain tumor cell lines, but negligibly when these cells were permeabilized, and it was ascribed similarly to impaired metabolism [50].

4.1.4 The possible role of glucokinase

The proposed feedback must act on a step in glucose oxidation that has significant control over the O module. Substantial in vitro and clinical data implicate glucokinase as such a step in β-cells [39]. Piragliatin, a glucokinase activator, has been shown to restore the diminished activation of cell respiration by glucose in human T2D islets and confer a supra-sensitized response to glucose equally in normal and T2D islets [23]. An intriguing (and testable) hypothesis that follows is that glucokinase activators override the endogenous feedback mechanism. A positive feedback within glycolysis has been suggested to contribute to the generation of slow, metabolic oscillations in islets, mediated by 6-phosphofructo-2-kinase/fructose- 2,6-bisphosphatase and possibly its interaction with glucokinase [51].

4.1.5 Assumptions and caveats in the control analysis

As shown here, the control structure of cellular energy metabolism can be quantified and interpreted with remarkably few experimental data points. We argue here that pairs of data points in Fig. 6 are sufficient to define the elasticities of each module. Elasticities are defined for infinitesimal changes, and thus are tangents to kinetic curves. Since log-log transformed proton leak and oligomycin-inhibited glucose oxidation curves in Fig. 6B approximate straight lines, the elasticity of these modules to ΔψM is minimally affected by the magnitude of ΔψM and accurately defined by the slopes of fit lines. In contrast, for the uninhibited O module, we have only two data points (2 or 10 mM glucose and the point representing the non-phosphorylating state) to calculate the elasticities of glucose oxidation to ΔψM. We lack sufficient information to predict how the elasticities change with ΔψM, although other modules have good linearity in log-log transformed data (and this is also typical in other studied systems until ΔψM is close to maximal [17,52]). Due to the expected shape of the kinetic curve in Fig. 6A we expect to slightly overestimate these elasticities when calculating from the step change. Because ${{}^{\ast }\epsilon }_{\mathrm{\Delta }\psi M}^O$ at 10 mM glucose is much larger than other elasticities, a slight overestimate will not alter our conclusions. We tested the effects of stochastic measurement errors on our conclusions, and we expect that the systematic bias due to this overestimate is small compared to stochastic errors. Similarly, the elasticity of the P module to ΔψM is calculated from two data points (2 and 10 mM glucose). Glucose may increase the flux through ATP turnover mostly through ΔψM (because downstream signaling is a function of ΔψM), so we do not expect one kinetic curve for the P-module at 2 mM glucose and another at 10 mM glucose, but (approximately) a single curve through the 2 and 10 mM glucose points. If the P-module is activated by glucose independently of ΔψM, then these two data points may lie on a pair of closely parallel kinetic curves, with the curve at 10 mM glucose higher (because of activation). However because the flux through the P module is virtually the same between 2 and 10 mM glucose (Fig. 6B), these curves collapse into a single curve through the 2 and 10 mM glucose data points. Furthermore, while we have determined ΔψM and respiration rate in an uninhibited condition only for 2 and 10 mM glucose, such concentration responses are known for β-cells in general, and these can be used to approximate the P+L curve connecting the 2 and 10 mM glucose points. Glucose-dependent activation of ΔψM and respiration follow similar sigmoid relationships. The published S_0.5 of glucose for OCR is 4.3 mM in human islets [23], and we measured an S_0.5 for ΔψM (in mV) 4.9±0.6mM (n=4; unpublished) in normal human β-cells and 5.5±0.4 mM in rats (n=3; from data in [25]). With the assumption of applicability of human β-cell data to INS-1 832/13 cells, these values translate to a straight or slightly convex P+L curve connecting 2 and 10 mM. Convexity slightly underestimates ${{}^{\ast }\epsilon }_{\mathrm{\Delta }\psi M}^P$ at 2 mM glucose and slightly overestimates it at 10 mM glucose when calculating elasticities from a straight line between the 2 and 10 mM glucose points, and would only strengthen our conclusion that the P module loses control over glucose oxidation at 10 mM glucose. Lastly, partial integrated responses require minimal experimental data to provide a qualitative assessment of activity and elasticity changes caused by a perturbation, because their calculation uses the control structure of the system only in the original steady state, and the steady state fluxes and intermediate levels of the perturbed system. Importantly, the small partial integrated response of ΔψM to glucose acting through the P module also suggests that the elasticity change in the P module between 2 and 10 mM glucose is small, implying little error in assuming the two elasticities are equal.

4.1.6 Comparison to mitochondria isolated from INS-1E cells

Proton leak exerts significant control over ΔψM and respiratory flux in INS-1E mitochondria, in striking contrast to muscle mitochondria, showing that proton leak is well suited to regulate ΔψM [42]. In this sense, the isolated mitochondrial system mimics the intact cell system at low glucose. However, we observed loss of this control at high glucose. This suggests that proton leak is well suited to regulate the null point of insulin secretion without interfering with the maximal response in high glucose. Our data suggests that the change in control happens by an energization-dependent activation of glucose oxidation. In contrast, in isolated mitochondria the activity of succinate oxidation is insensitive to ATP/ADP [42], suggesting that if ATP/ADP is the factor responsible for the positive feedback in cells, it acts upstream of succinate dehydrogenase.

5 Conclusion

The metabolic control analysis described here reveals a positive feedback due to an energization-dependent activation of glucose oxidation that amplifies changes in ΔψM and therefore in ATP/ADP as glucose concentration rises. We propose that this is essential for the proper regulation of GSIS, and that it is dysfunctional in T2D β-cells, at least in the small group of studied individuals [16,23]. At low glucose the positive feedback has weak effects, allowing relatively strong control over the magnitude of ΔψM by glucose oxidation, proton leak and ATP turnover, and a relatively high contribution of proton leak to homeostasis of ΔψM. However, at high glucose the feedback loop fully engages, and control over the magnitude of ΔψM by glucose oxidation, proton leak and ATP turnover is greatly diminished, and homeostatic control shifts almost entirely to glucose oxidation. The magnitude of ΔψM at high glucose concentrations is relatively insensitive to ATP turnover, thus preventing ion transport and macromolecule synthesis from interfering with GSIS. These data resolve a long-standing puzzle related to the relatively high proton leak observed in insulinoma cells. A large proton leak seemingly conflicts with GSIS, as it short-circuits energy metabolism and decreases ATP/ADP. However, our analysis indicates that proton leak can control ΔψM more strongly in the fasting state than under high glucose, which could be a means for attenuating insulin secretion during fasting without affecting maximal secretion, since control shifts away from proton leak at high glucose concentrations.

Altogether, the observed kinetic characteristics and positive feedback loop and the consequent control structure of insulinoma cell energy metabolism appear well-suited to support GSIS, because they allow a strong amplification of responses of ΔψM and GSIS to small changes in glucose concentration. We suggest that disruption of this fine control can explain the damaged GSIS characteristic of β-cells in previously observed cases of T2D. The assay technology and analysis described here will allow identification of the feedback factor, its target and the precise role of this loop in T2D.

Highlights.

• We applied control analysis to mitochondrial energy metabolism in insulinoma cells

• Glucose oxidation is amplified by a positive feedback by factors downstream of ΔψM

• At high glucose, ΔψM is set by glucose oxidation, not by bioenergetic demand

• Proton leak may contribute to setting ΔψM only in low glucose

Abbreviations

a_R’

activity coefficient ratio

CDC

complete depolarization cocktail

ΔψM

mitochondrial membrane potential

ΔψP

plasma membrane potential

FCCP

carbonyl cyanide-4-(trifluoromethoxy)phenylhydrazone

GSIS

glucose-stimulated insulin secretion

K_ATP

ATP-sensitive K⁺-channels

MDC

mitochondrial depolarization cocktail

OCR

oxygen consumption rate

PM

potentiometric medium

PMK

K⁺-based potentiometric medium

PMPI

ΔψP indicator

SE

standard error

T2D

type 2 diabetes mellitus

TMRM

tetramethylrhodamine methyl ester

TPB

tetraphenylborate

V_F,

mitochondria:cell volume fraction