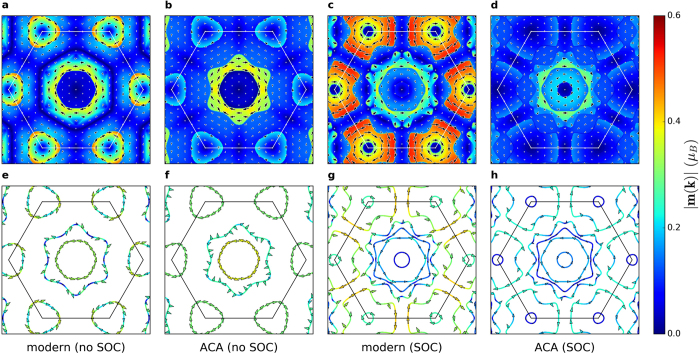
Figure 4. In-plane orbital moment (OM) in BiAg₂ from first principles.

(a–d) Summing up the individual contributions of all occupied bands below the Fermi energy, we obtain the distribution of the in-plane OM m(k) in k-space. (e–h) The in-plane OM directly at the Fermi surface, which is important to orbital magnetoelectric response. In all cases, colors represent the magnitude |m(k)|, arrows indicate the in-plane direction of the OM with the arrow size proportional to |m(k)|, and thin lines mark the Brillouin zone. The results of both Berry phase theory (modern) and atom-centered approximation (ACA) are shown with and without taking into account spin-orbit coupling (SOC). The in-plane OM within the two approaches deviates drastically around the K-point, and the modern theory predicts overall a richer structure.