Fig. 1. Steps in the PDE functional identification of nonlinear dynamics (PDE-FIND) algorithm, applied to infer the Navier-Stokes equations from data.
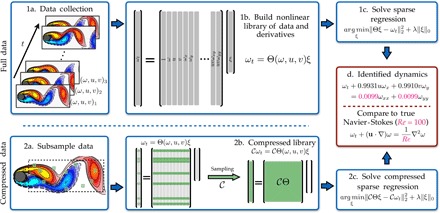
(1a) Data are collected as snapshots of a solution to a PDE. (1b) Numerical derivatives are taken, and data are compiled into a large matrix Θ, incorporating candidate terms for the PDE. (1c) Sparse regressions are used to identify active terms in the PDE. (2a) For large data sets, sparse sampling may be used to reduce the size of the problem. (2b) Subsampling the data set is equivalent to taking a subset of rows from the linear system in Eq. 2. (2c) An identical sparse regression problem is formed but with fewer rows. (d) Active terms in ξ are synthesized into a PDE.
