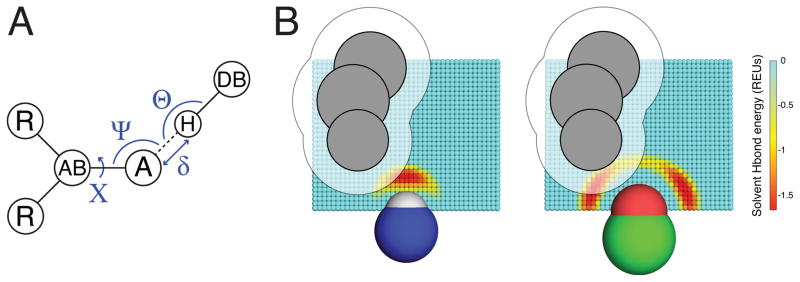
Figure 1. The SHO model for polar solvation.

A) The geometry-dependence of hydrogen bonding, as exemplified through the degrees of freedom used by the hydrogen bond term in Rosetta energy function. The distance δ and the angles Θ, Ψ and X are defined with respect to the acceptor atom “A”, the hydrogen bond donor “H”, and the atoms to which each of these are connected “AB” and “DB”. B) For SHO calculations, a cubic grid is built around the polar group of interest: a probe water molecule can occupy any of these points, or else one of many degenerate locations in bulk solvent (not shown). Grid points are colored based on the hydrogen bond energy of a probe water molecule placed at that location (expressed in Rosetta Energy Units, REUs); the energetics captured on the grid thus reflect the preferred hydrogen bonding geometry for the polar atom of interest, as shown for this donor (left) and acceptor (right). Neighboring atoms (grey) sterically occlude the probe water from certain locations; these points correspond to those covered by the atoms themselves, and also to the regions too close to these atoms to be accessible to the probe water (grid points covered by the transparent area). By summing over these occluded locations, we explicitly evaluate the desolvation free energy as described in Equation 5.