Accelerating Bayesian inference for evolutionary biology models

Abstract

Motivation

Bayesian inference is widely used nowadays and relies largely on Markov chain Monte Carlo (MCMC) methods. Evolutionary biology has greatly benefited from the developments of MCMC methods, but the design of more complex and realistic models and the ever growing availability of novel data is pushing the limits of the current use of these methods.

Results

We present a parallel Metropolis-Hastings (M-H) framework built with a novel combination of enhancements aimed towards parameter-rich and complex models. We show on a parameter-rich macroevolutionary model increases of the sampling speed up to 35 times with 32 processors when compared to a sequential M-H process. More importantly, our framework achieves up to a twentyfold faster convergence to estimate the posterior probability of phylogenetic trees using 32 processors when compared to the well-known software MrBayes for Bayesian inference of phylogenetic trees.

Availability and Implementation

https://bitbucket.org/XavMeyer/hogan

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Model inference and hypothesis testing is nowadays widely performed using Bayesian inference. The surge of popularity of this statistical method is tightly linked with the theoretical and computational developments of Markov chain Monte Carlo methods (MCMC; Hastings, 1970; Metropolis et al., 1953). Indeed, MCMC made possible the numerical approximation or sampling of high-dimensional posterior distribution, thus broadening the inference of more complex statistical models. Evolutionary biology particularly benefited from this progress and a large number of applications, ranging from phylogenetic reconstructions (Lartillot et al., 2013; Ronquist et al., 2012), divergence time analyses (Drummond et al., 2006), molecular evolution (Dib et al., 2014), comparative methods (Beaulieu et al., 2012; FitzJohn, 2012) or population genetics (Kuhner, 2006; Fischer et al., 2011), makes extensive use of these MCMC approaches.

While popular, MCMC is limited by its inherent sequential nature and its dependency on user defined transition kernels. Moreover, complex models require costly computational evaluations of their likelihood function and their high-dimensional parameter-space is usually difficult to explore efficiently. A wide variety of approaches have been proposed to improve the sampling of some of these complex models. These solutions range from avoiding the evaluation of the likelihood function (Marjoram et al., 2003; Mengersen et al., 2013) to using sequential Monte Carlo (Andrieu et al., 2010; Cappe et al., 2007) or Hamiltonian Monte Carlo methods (Duane et al., 1987; Neal, 2011). However, these methods suffer from limitations that make them less generally applicable. For example, some have to be applied on a model-specific basis, may prove difficult to apply to high-dimensional parameter-space or require continuous parameters. These limitations are typical of Bayesian inference in phylogenetics. Indeed, the computational complexity of tree building grows with the length of the sequence data available as well as with the number of taxa, which also defines the amount of parameters and potential phylogenetic trees to consider (Felsenstein, 2004). Moreover, it is well known that sampling from this discrete space of phylogenetic trees is a particularly difficult task (Bouchard-Côté et al., 2012; Lakner et al., 2008).

Current approaches to build phylogenetic trees therefore still heavily relies on MCMC and any enhancements of these methods would be extremely useful for evolutionary biologists. Several studies focused on the sampling effectiveness (or mixing) of the MCMC process and helped to propose theoretical guidelines to specify the optimal size for transition kernels based on normal distributions (Gelman et al., 1996; Roberts et al., 1997). These guidelines were used to develop the adaptive Metropolis algorithm (Haario et al., 2001), which aims at optimally tuning a transition kernel using the observed empirical covariance of the Markov chain. The adaptive Metropolis method has been further improved by using component-wise scaling (Haario et al., 2005), adaptively tuning the proposal size to target an optimal acceptance rate (Andrieu and Thoms, 2008) or exploiting the parameter covariance (Roberts and Rosenthal, 2009; Vihola, 2012). Some of these improvements have been implemented in the main software to build phylogenetic trees (Aberer et al., 2014; Drummond et al., 2012; Ronquist et al., 2012).

However, few strategies were explored to improve MCMC efficiency by exploiting parallel computing. While some of these methods offer interesting properties, they usually suffer from limitations that hinder their general use on applied problems. For example, prefecthing (Brockwell, 2006) aims at predicting the future states of the Markov chain to pre-process them in parallel. This method is however limited by the difficulty of accurately predicting the path of the Markov chain. We refer the reader to the recent review of Green et al. (2015) for an extensive state-of-the-art description of this domain.

We present here a novel combination of enhancements of the Metropolis-Hastings (M-H) framework specifically designed to obtain an efficient sampling of parameter-rich and complex models. We first present a multivariate adaptive proposal that coerces the acceptance rate, balances the mixing among all parameters and exploits their potential correlations. We then show that under a precise coupling of both adaptive MCMC and pre-fetching, we can achieve synergetic performance gains that exceed the sum of its parts. Finally, the framework properties are validated on various test cases and is then challenged on two real biological applications: a macroevolutionary model (Silvestro et al., 2014b) and on a model for Bayesian inference of the phylogeny (Felsenstein, 2004).

2 Methods

2.1 Background and notation

Starting from data X and a model M with unknown parameters $\Theta \in {ℝ}^d$, we are interested in sampling the posterior distribution

$$p(\Theta |X)=\frac{f(\Theta )·f(X|\Theta )}{\int f(\Theta )·f(X|\Theta )}$$

or its unnormalized density $\pi (\Theta )\propto f(\Theta )·f(X|\Theta )$. Sampling this distribution can be done by setting a Markov chain with $\pi (\Theta )$ as stationary distribution. This is done by considering a reversible Markov chain whose transition kernel $p(\Phi ,\Theta )$ satisfies the detailed balance equation

$$\pi (\Theta )p(\Theta ,\Phi )=\pi (\Phi )p(\Phi ,\Theta )\hspace{1em}\hspace{1em}\forall \hspace{0.17em}(\Theta ,\Phi )$$

The kernel p is based on two functions: an arbitrary transition kernel $q(\Phi ,\Theta )$, also known as proposal window, and an acceptance probability $\alpha (\Theta ,\Phi )$. The probability of leaving the state Θ is given by

$$p(\Theta ,\Phi )=q(\Theta ,\Phi )\alpha (\Theta ,\Phi )$$

with $\Theta \ne \Phi$, while the probability of staying in the same state is then given by

$$p(\Theta ,\Theta )=1-\int q(\Theta ,\Phi )\alpha (\Theta ,\Phi )d\Phi$$

Hastings (1970) proposed the following acceptance ratio

$$\alpha (\Theta ,\Phi )=\text{min}\left(1,\frac{\pi (\Phi )q(\Phi ,\Theta )}{\pi (\Theta )q(\Theta ,\Phi )}\hspace{0.17em}\right)$$

which simplifies to the original algorithm of Metropolis et al. (Metropolis et al., 1953) if the transition kernel q is symmetrical.

2.2 An efficient multivariate adaptive proposal

Our framework uses its own multivariate adaptive proposal specifically designed to maintain a low computational cost while exploiting the potential correlations between parameters in complex and parameter-rich models.

The original adaptive method presented by Haario et al. (2001) defines the proposal as $\Phi \sim \mathcal{N}(\Theta ,\lambda \Sigma )$ with λ being the optimal scaling factor (Gelman et al., 1996) and Σ the observed empirical covariance of the Markov chain. While being based on the same concepts, our adaptive process approximates the covariance matrix Σ using stochastic approximation methods and optimizes the mixing by coercing the acceptance rate (Andrieu and Thoms, 2008). Given the sample ${\Theta }^t$ observed at iteration t of the MCMC process, the global scaling factor λ, the parameter mean $\overline{\Theta }$ and covariance Σ are updated as follow

$$\begin{array}{l}\begin{array}{c}{\overline{\Theta }}^{(t+1)}={\overline{\Theta }}^{(t)}+{\gamma }^{(t)}·({\Theta }^{(t)}-{\overline{\Theta }}^{(t)})\end{array}\\ \begin{array}{c}{\Sigma }^{(t+1)}={\Sigma }^{(t)}+{\gamma }^{(t)}·[({\Theta }^{(t)}-{\overline{\Theta }}^{(t)})\otimes \end{array}\\ \begin{array}{c}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}({\Theta }^{(t)}-{\overline{\Theta }}^{(t)})-{\Sigma }^{(t)}]\end{array}\\ \begin{array}{c}\hspace{0.17em}\text{log}\hspace{0.17em}({\lambda }^{(t+1)})=\hspace{0.17em}\text{log}\hspace{0.17em}({\lambda }^{(t)})+{\gamma }^{(t)}({\overline{\alpha }}^{(t)}-{\alpha }_{\mathrm{\star }})\end{array}\end{array}$$ (1)

with ${\alpha }_{\mathrm{\star }}$ defining the target acceptance rate that optimizes the mixing (Roberts et al., 1997) and ${\overline{\alpha }}^{(t)}$ being the average observed acceptance rate after t iterations.

The step size γ impacts the convergence of the approximation process and must have the following two properties (Robbins and Monro, 1951): ${\sum }_{t=0}^{\infty }{\gamma }^{(t)}=\infty$ and ${\sum }_{t=0}^{\infty }{({\gamma }^{(t)})}^2<\infty$. Sequences defined as ${\gamma }^{(t)}=C/t^{\beta }$ with $\beta \in [{(1+\eta )}^{-1},1]$ satisfy these conditions and their rate of convergence is determined by the two user-defined constants C and η.

Coercing the global scaling factor λ guarantees that the overall proposal acceptance rate is optimal by taking advantage of the information made available by the MCMC process. However, it does not ensure a balanced mixing over all parameters. Component-wise scaling is able to solve this problem at the cost of d additional likelihood evaluations (Haario et al., 2005). The new component-wise or local scaling factors $\Lambda =diag({\lambda }_1,\dots ,{\lambda }_d)$, estimated separately for each parameters, can then be used to scale the proposal over each dimension (corresponding to a parameter) as follows:

$$\Phi \sim \mathcal{N}(\Theta ,{\Lambda }^{1/2}\Sigma {\Lambda }^{1/2})$$

This approach guarantees a more balanced mixing over all parameters while inducing a significant increase in computational cost. A second drawback is the loss of control on the global acceptance rate. Indeed, independent parameters would lead to a global acceptance rate defined as $\alpha ={\prod }_{i=1}^d{\alpha }_i$. However, in the more frequent case of correlated parameters, the relation between local acceptance rates α_i and the global acceptance rate α remains undefined.

In order to efficiently balance the mixing along all parameters, our adaptive proposal combines both local and global scaling variants. This proposal maintains the coercion of the global acceptance rate by using the global scaling λ, which is updated at each iteration. Component-wise updates are made periodically and the normalized scaling factors $w_i={\lambda }_i/{\sum }_{k=1}^d{\lambda }_k$ form the local scaling matrix $W=diag(w_1,\dots ,w_d)$. The proposal then uses the global scaling to target the overall size of the move while the normalized local scaling ensures a balanced mixing over all directions.

$$\Phi \sim \mathcal{N}(\Theta ,\lambda W^{1/2}\Sigma W^{1/2})$$ (2)

The method that we propose can still be improved when the parameters Θ are correlated (Gilks et al., 1995). These correlations are exploited by using the geometric interpretation of the multivariate normal distribution. Since this distribution belongs to the family of elliptical distributions, it can be expressed by the directions of the principal axes of the ellipsoids. The spectral decomposition of the covariance matrix

$$\Sigma =QEQ\prime =Q{E}^{1/2}(Q{E}^{1/2})\prime$$

gives these directions as the eigenvectors $Q=(V_1,\mathrm{..},V_d)$ and their scaling as the eigenvalues $E=diag(e_1,\mathrm{..},e_d)$. We can then sample from the distribution

$$X\sim \mathcal{N}(\mu ,\Sigma )\equiv \mu +Q{E}^{1/2}\mathcal{N}(0,I)$$

The component-wise scaling factors are used in this case to scale the size of the moves along the direction of the eigenvector V_i and the scaled eigenvectors ${(\lambda \tilde{W}E)}^{1/2}$ can be used to build the following proposal

$$\Phi \sim \Theta +Q{(\lambda \tilde{W}E)}^{1/2}\mathcal{N}(0,I)$$ (3)

Our method is still limited by its additional computational cost that grows polynomially with the number of dimensions d. The covariance matrix is costly to learn since it requires linear algebra functions with complexity $\mathcal{O}(d^2)$. In addition, the generation of random moves based on multivariate distributions requires the Cholesky or eigen-decomposition of the scaled covariance matrix at a computational cost of $\mathcal{O}(d^3)$. The decomposition must be updated whenever Σ and Λ change.

We created smaller blocks of parameters to reduce the computational burden and monitored the convergence of the adaptive phase (see supporting materials). Moreover, our adaptive proposal evolves with the information contained in the covariance matrix. In the initial phase, parameters are considered independent. The covariance matrix is learned as usual but moves are independently generated from

$$\Phi \sim \mathcal{N}(\Theta ,\lambda W^{1/2}\tilde{\Sigma }{W}^{1/2})\hspace{1em}\hspace{1em}\hspace{0.17em}\text{with}\hspace{0.17em}\hspace{1em}\hspace{1em}\tilde{\Sigma }=diag({\sigma }_1^2,\dots ,{\sigma }_d^2),$$ (4)

which avoids the Cholesky or eigen-decomposition step. Upon convergence detection of Σ, the observed degree of correlation between parameters is assessed. If no significant correlations are detected, the training phase ends. Otherwise the proposal is switched to a proposal based on the full Σ matrix (Eqs. (2) or (3)) and the training phase is prolonged until a second convergence is reached.

2.3 Securing an optimal pre-fetching

Our adaptive proposal greatly improves the mixing properties of the MCMC, but it can also enhance the performances of a parallel MCMC method. Markov chains are an inherently sequential process due to the dependencies between states in two subsequent iterations of a chain. Obtaining speed improvements by using parallel computing techniques is therefore an important challenge. Pre-fetching (Brockwell, 2006) overcomes this limitation by pre-processing the possible paths that the Markov chain could take during a set of iterations.

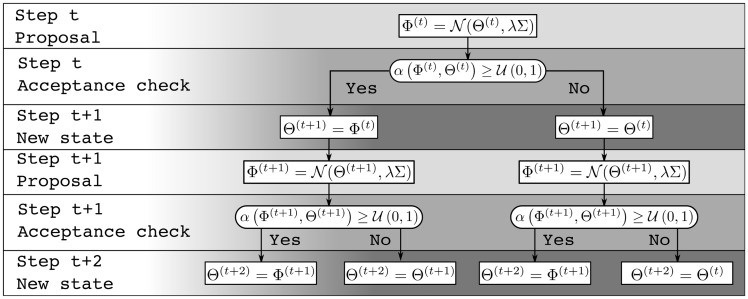
The future path of a MCMC can be represented as a decision tree (Fig. 1). Given that the chain at time t is in state ${\Theta }^{(t)}$, a new state ${\Phi }^{(t)}$ is proposed. This new state is then accepted or rejected with probability $\alpha ({\Theta }^{(t)},{\Phi }^{(t)})$. Branches of the tree represent these two possible paths of the MCMC process. Each state, or node, leads to two subtrees corresponding to either an acceptance or a rejection.

Fig. 1.

Markov chain’s decision tree of depth k = 3

The likelihood computation of the future possible states $\Phi$ can then be distributed over multiple processors. Given that several samples are generated during the same amount of time that it previously took for one, this results in a significant speed up. However, given the tree structure of the possible paths of the Markov chain, an exhaustive approach to get D = k useful samples, or draws, per pre-fetching iterations would require $n_p=2^k-1$ processors. This strategy scales poorly since the number of wasted likelihood computations corresponding to unvisited state grows exponentially with k.

Various strategies (Strid, 2010) aiming at determining the most probable path in the decision tree have been proposed to improve the scaling of this method. One of these strategies uses the mean observed acceptance rate of the chain $\overline{\alpha }$ as a predictor for the most probable paths. As defined in (Strid, 2010, Eq. 8), the efficiency of this method can be estimated by a performance model that depends on the acceptance rate and the number of available processors:

$$E(\alpha ,n_p)=E^1(\alpha )·D(\alpha ,n_p)$$ (5)

where $E^1(\alpha )$ defines the mixing efficiency for an i.i.d normal distributed proposal with $d\to \infty$ (Strid, 2010, Eq. 7) and $D(\alpha ,n_p)$ is the expected number of draws per pre-fetching iterations (Strid, 2010, Eq. 1).

The expected number of draws $D(\alpha ,n_p)$ is equal to $n_p$ and thus optimal for α = 0 or α = 1. With such α, pre-fetching is indeed able to exactly predict the path of the Markov chain by considering moves as being always rejected, respectively accepted. Such prediction would be represented by the right most, respectively left most, branch in the decision tree (Fig. 1). The expected number of draws $D(\alpha ,n_p)$ reduces as α approaches 0.5, since predictions are less accurate. When α reaches 0.5, any path in the decision tree is equally probable and thus pre-fetching is back to using the inefficient exhaustive approach of computing all the possible paths ($D={\text{log}}_2{n}_p$).

On the other hand, the mixing efficiency of a proposal $E^1(\alpha )$ peaks at an optimal α value of 0.234 with $d\to \infty$ (Roberts and Rosenthal, 2001). Therefore, the optimal acceptance rate ${\alpha }_{\mathrm{\star }}$ for a given number of processors can be derived from equation 5 and expresses the optimal trade-off between an efficient mixing and accurate predictions for pre-fetching. In others words, the efficiency of both method is then controlled by the average acceptance rate α of the proposals and is optimal for ${\alpha }_{\mathrm{\star }}$.

Therefore, we coupled pre-fetching to our adaptive proposals by coercing their acceptance rate to the value ${\alpha }_{\mathrm{\star }}$ optimizing equation 5 through the global scaling factor λ. Although we do not know a priori the acceptance rate of the MCMC process, this approach ensure that it will quickly reach the vicinity of the target acceptance rate ${\alpha }_{\mathrm{\star }}$. This combination of methods will optimize the efficiency of the pre-fetching method by finding the optimal size of the proposal window in function of the number of available processors and regardless of the model.

In return of providing these optimal conditions for the pre-fetching method, the adaptive proposal also benefits from this coupling. During a pre-fetching iteration, only a certain number of predicted states are retained, while the remaining unused ones are discarded. However, our adaptive proposal takes advantage of these wasted likelihood evaluations. During one iteration, all the acceptance rates α estimated to predict the chain path in the decision tree offer usable information that can help the updating of λ. The advantage is that the training process becomes more accurate and adapts more quickly to the parameter space, because λ is adapted more frequently. This results in a better sampling efficiency and reduces the time required to reach the equilibrium of the Markov chain, also known as burn-in phase. These improvements apply equally well, if not better, to the local scaling factors Λ by processing the unidimensional moves in parallel and thus offering a nearly ideal speed-up of this costly operation (see Algorithm 1 in the supplementary materials for an outline of the main steps taking place during an iteration of the presented method).

2.4 Assessing the framework performance

In a first phase, we compare, using simple models, multiple strategies to highlight the contributions of each enhancement that are at the core of our new framework. Two strategies using non-adaptive random walk M-H with pre-fetching method are used as reference: the PF method emulates user-defined proposal windows by using relevant but sub-optimal size of the proposals, while OPPF uses optimal proposal windows that are scaled based on Eq. (5) and guidelines from Roberts and Rosenthal (2001) to target the optimal acceptance rate ${\alpha }_{\mathrm{\star }}$. These two methods are compared with variants of our new framework based on pre-fetching and adaptive proposal scaled locally and globally. The three variants STD, MIXED and PCA correspond to the three proposals described by Eqs. (4), (2) and (3), respectively. These experiments and their results are detailed and discussed in the supplementary materials.

In a second phase, we challenge our best strategy PCA on a macro-evolutionary model (Silvestro et al., 2014a) on a large empiric dataset. Then, our framework is compared with the widely used MrBayes software (Ronquist et al., 2012) on a codon-substitution model with fixed tree topology as well as on the task of inferring trees with a nucleotide model. The complexity of these models and the fact that MrBayes already incorporate a form of adaptive proposals offer a more instructive benchmark (all measures were made using MrBayes 3.2.5 compiled with SSE support and MPI enabled). Furthermore, while MrBayes was chosen as a reference, the performance gains measured in this benchmark result from the presented enhancements of the MCMC method and thus should apply similarly to any alternative software independently of the efficiency of the likelihood computations.

2.4.1 Performance measures

We measured the efficiency in two ways. We first estimated the sample size (ESS; Liu, 2008) that gives an indication of the potential number of usable samples. This number is defined as the ratio between the total number of samples and their integrated auto-correlation time (ACT). Then, in order to properly assess the performance of our framework on the inference of trees, we measured the convergence rate of the phylogenetic tree distribution using the average standard deviation of split frequency (ASDSF; Lakner et al., 2008). The overall performance of the framework is measured using the speedup S defined as

$$S=\frac{\overline{g}(n_p,M)}{\overline{t}(n_p,M)}÷\frac{\overline{g}(1,M_R)}{\overline{t}(1,M_R)}$$ (6)

with the $\overline{g}(n_p,M)$ being the averaged measures (i.e. ACT or ASDSF), $\overline{t}(n_p,M)$ the averaged run time for n_p processors and the method M. We mainly compare the measures of each method M to the reference method M_R with 1 processor. The speedup indicates the gain provided by the increase in mixing or rate of convergence in addition of the loss caused by the additional time spent during the adaptive phase plus the overhead of the communications between processors.

2.4.2 Hierarchical bayesian model

The model PyRate (Silvestro et al., 2014a) is used to illustrate the actual performance of our methods on simulated and real datasets. This hierarchical Bayesian model analyses speciation and extinction rates of large collections of fossils and estimates large numbers of parameters including the preservation rate, the time of speciation and extinction of each species and the speciation and extinction rates with their variation trough time. This model has a complexity order of $\mathcal{O}(N)$ and only few parameters are correlated. These properties are particularly interesting because the relatively inexpensive likelihood will highlight the overhead of the framework, while the low amount of correlations will illustrate its ability to exploit correlations.

Our framework was challenged on a large dataset of plant fossils (Silvestro et al., 2015). This dataset contains 22 415 fossil occurrences assigned to 443 plant genera. It spans over a hundred millions of years divided in 31 predefined epochs, which were defined by the stratigraphic geological time scale.

2.4.3 Codon-substitution model

We use the well-known model of codon substitutions M2a, which was developed to identify positive selection on protein coding genes, to illustrate the mixing performance of our framework on methods for molecular evolution (Yang et al., 2000). Given a fixed phylogenetic tree and a set of protein coding sequences, the M2a model estimates the selective pressure on codon sites through the use of a mixture of three site-classes having different synonymous to non-synonymous substitution rates ω: purifying selection (${\omega }_0<0$), neutral evolution (${\omega }_1=1$) and positive selection (${\omega }_2>1$). Beside the estimation of the parameter values for each site-class ω and their respective proportions, this model estimates the overall transition-transversion rate and the branch lengths of the tree. The computational cost of the M2a model exceeds significantly the cost of the PyRate model since it requires matrix exponentiations and matrix-matrix operations (both having a complexity order of $\mathcal{O}(N^3)$) that depends on the alignment length and the tree size. It thus offers a completely different sampling challenge than the one of PyRate.

The performance of our framework was tested by computer simulations. We used two simulated datasets created using INDELible (Fletcher and Yang, 2009). These datasets represented alignments formed of 100 codons simulated under mild purifying selection ($\omega =0.8$) on phylogenetic trees having 16 taxa (Dataset 1) and 32 taxa (Dataset 2). We took particular care to ensure an informative comparison of our implementation with MrBayes. The simulated phylogenetic tree was used as a fixed tree topology and the MC³ method was disabled. Under this circumstance, our implementations and MrBayes sampled the same set of parameters and both used adaptive proposals.

2.4.4 Estimating phylogenetic trees distribution

As a final illustration, we challenged our framework with the estimation of the posterior distributions of phylogenetic trees with their branch lengths and parameters of a general time reversible (GTR) model of nucleotide substitution (Tavaré, 1986). This substitution model presents a lesser computational challenge than the codon model M2a. However, the major difficulty resides in properly sampling the space of potential phylogenetic trees. This tree space grows exponentially with the number of taxa and can only be explored with specific tree proposals (Felsenstein, 2004). For that matter, we implemented two widely used tree proposals: the Stochastic Nearest Neighbor Interchange (stNNI) and the Extending Subtree Pruning and Regrafting (eSPR) in our framework.

We compared our framework performance to MrBayes under two different settings. In the first setting, later referred as Ref MrBayes, only the stNNI and eSPR tree proposals were enabled to mimic our own implementation. In the second setting, later referred as Full MrBayes, the default configuration of MrBayes was used.

All the aforementioned settings (including our framework) were compared with and without the MC³ method on two empirical DNA datasets used in Lakner et al. (2008) and available in TreeBASE (http://www.treebase.org). The first one, M2017 (legacy ID M336) has 27 taxa and 1949 sites, while the second dataset, M2152 (legacy ID M520) has 67 taxa and 1098 sites. Finally, to give an insight of our method potential on larger dataset, we used a DNA empirical dataset published by Pyron and Wiens (2011) representing over 2800 species of amphibians with more than 10 000 sites.

3 Results and discussion

3.1 Performance gain on PyRate model

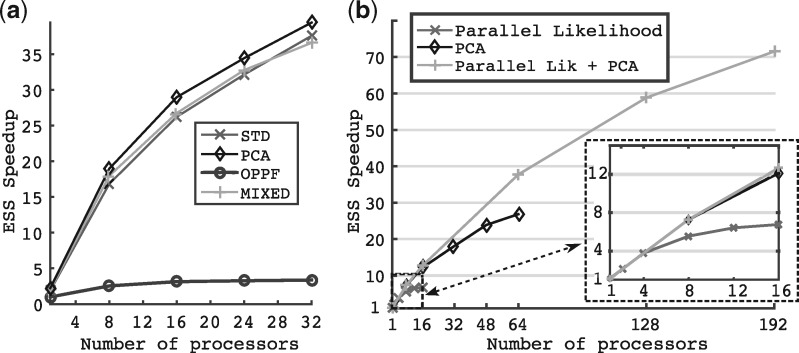
We challenged our new framework by analysing a large dataset of plant fossils (Silvestro et al., 2015) with PyRate. The complex and heterogeneous parameter space of the empirical model highlighted the full potential of our new framework. Adaptive methods revealed speedups between 2 to over 35 times when compared to the non-adaptive OPPF method depending on the number of processors used (Fig. 2a). PCA surpassed the other adaptive methods by exploiting the small amount of correlation that existed in the model.

Fig. 2.

Result for PyRate model on plant fossils data. The figure on the left shows the speedup of each method using OPPF with 1 processor as the reference. The right figure shows the parallel scalability of the framework when compared or combined to a parallel computation of the PyRate likelihood. Settings for these simulations were $d\approx 1000,\hspace{0.17em}8\times {10}^6$ iterations and 3 runs

In this application, the number of free parameters to estimate was approximately 1000, which makes it almost impossible for a user to guess a sensible set of proposal distribution for this real dataset. Indeed, the mean variance of the observed chain for species birth and death times ranged from 1 to 425 with average value of 138 and standard deviation of 110. Using the average variance to define the proposal distribution would result in some parameters being nearly never sampled. Actually moves configured with the observed average variance would be rejected almost all the times when applied to parameters with variances one hundred-fold smaller. We therefore fixed an arbitrary size for proposal distribution of $\approx 5$ for OPPF, which allowed each parameter to be sampled.

To illustrate the gains of the adaptive methods, let us consider the case where we would like to sample this model with an average ESS of 500 per parameter. The runtime of such a task can be estimated by adding the time T_BI spent in the burn-in to the estimated sampling time T_S. The former is directly measurable, while the latter can be estimated based on the desired number N_ESS of ESS and the average observed time T_ESS required to produce one ESS. Therefore, the time to produce an average of 500 ESS using the PF method with one processor would be given by

$$\begin{array}{c}{T}_{PF}=T_{BI}+T_S=T_{BI}+N_{ESS}·T_{ESS}\\ =1600+500·47=2.35·{10}^4\hspace{0.17em}\text{seconds}\hspace{0.17em}\end{array}$$

(i.e. 7 h). Switching to the PCA method, it would take only two and a half hours to reach the same level of ESS on one processor ($T_{BI}=2670,S=12$) and the time would reduce to 17 minutes if 16 processors ($T_{BI}=230,S=1.6$) would be used.

Beside the differences in computation time, the OPPF method would further produce a highly uneven sampling of all parameters due to the suboptimal proposal distributions. This was illustrated by the variation of ACT over all parameters. We observed an average ACT of 740 with standard deviation of 877 for the PF method. The PCA method produced in contrast a far more reliable quality of sampling and its ACT variation reached only 193 ±273 for 1 processor and 219 ±177 for 16 processors.

3.1.1 Comparison with parallel likelihood

We measured the raw parallel performance gain of our framework when confronted or combined to a parallel computation of the PyRate likelihood. We thus compared the performance of the PCA adaptive proposal combined with a) a parallel likelihood, b) pre-fetching (our framework) and c) both methods.

Our framework performance (variant b) clearly surpassed the parallel likelihood one. It showed a nearly linear speedup up to 8 processors and notable gains up to 48 processors, while the parallel likelihood (variant a) showed a nearly linear speedup up to 4–6 processors before reaching a plateau with no gain in performance (Fig. 2b). The combination of both methods (variant c) showed the potential of coupling model dependent improvements with our framework by greatly increasing the parallel scalability and reaching speedups of $\approx 40$ for 64 processors and $\approx 60$ for 128 processors.

For this measures, we used the PCA proposal as the reference method in order to measure the parallel scalability without being biased by the gain induced by our adaptive proposals. Thus the speedup was measured according to Eq. (6) with $M_R=$PCA using the PyRate model on the plant fossil dataset.

3.2 Performance gain on phylogenetic models

3.2.1 Mixing on codon-substitution models

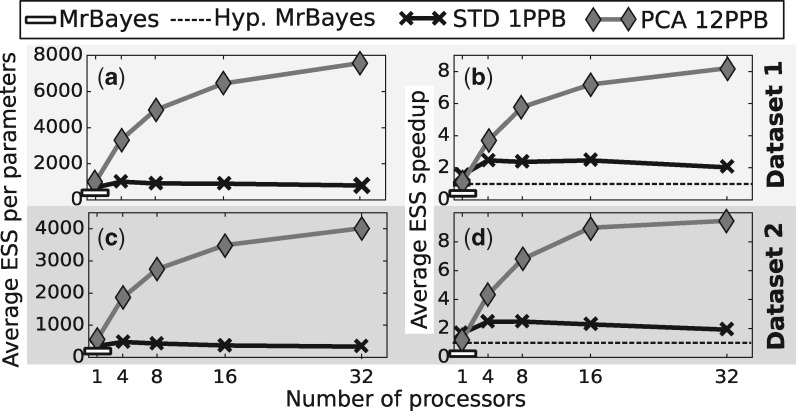
We assessed the performance of our framework on the M2a model of codon substitutions with simulated data. As a reference, we compared a sequential execution of STD with one parameter per block against the adaptive MCMC based algorithm implemented in MrBayes. The average ESS obtained were comparable, yet slightly better for our STD variant (Fig. 3a and c). We then compared our best method, PCA, with 12 parameters per block and showed an improvement in sampling performances. Indeed, the increase of average ESS when compared to MrBayes went from more than a twofold factor on a sequential execution up to a twentyfold factor with 32 processors.

Fig. 3.

Result for the ESS and ESS speedup comparison with MrBayes on the M2a codon substitution model with simulated data. (a) and (c) The average ESS per parameter on the first, respectively second, datasets for MrBayes, the STD method using single parameter moves and the PCA method with multiples parameters per block. (c) and (d) The ESS speedup for the same methods on the same datasets using an hypothetical MrBayes implementation as reference. Simulations were run for $2·{10}^5$ iterations

While representing the mixing efficiency of these methods, the ESS does not take into account the added computational complexity brought by moving multiple parameters at once. Indeed, Bayesian software for phylogenetic inference such as MrBayes are taking advantage of the possibility to partially update the likelihood when one or few parameters are changed. The computational cost during an iteration is then linked to the amount of parameters updated. Therefore, using the ESS speedup defined by Eq. 6 is more appropriate given that it encompasses these increases in computational cost by normalizing the ESS by the execution time. However, since our implementation outperformed MrBayes on this model (see supporting materials), we had to define as reference, M_R, an Hypothetical MrBayes by defining the average reference ESS, $\overline{g}(1,M_R)$, as the one of MrBayes and the average runtime, $\overline{t}(1,M_R)$, as the one of our STD implementation. The reference thus represents the effective sample size of MrBayes normalized by the runtime of our method with settings closest to MrBayes (i.e. updating only one parameter per iteration).

The obtained ESS speedups (Fig. 3b and d) show that our implementation were still outperforming the hypothetical reference method from close to a twofold factor on a sequential execution and up to approximately a tenfold factor with 32 processors. However, in the sequential case, the simple STD method was more efficient than the PCA variant. This is explained by considering the overhead of more costly partial likelihood computations and the added cost of learning parameters correlation. However, as soon as several processors were used, and thus our coupling of the adaptive proposals with the pre-fetching method was employed, the PCA variant was more efficient by proposing bolder moves and using the parallel resources to learn correlations more accurately and quickly.

3.2.2 Convergence on phylogenetic tree distributions

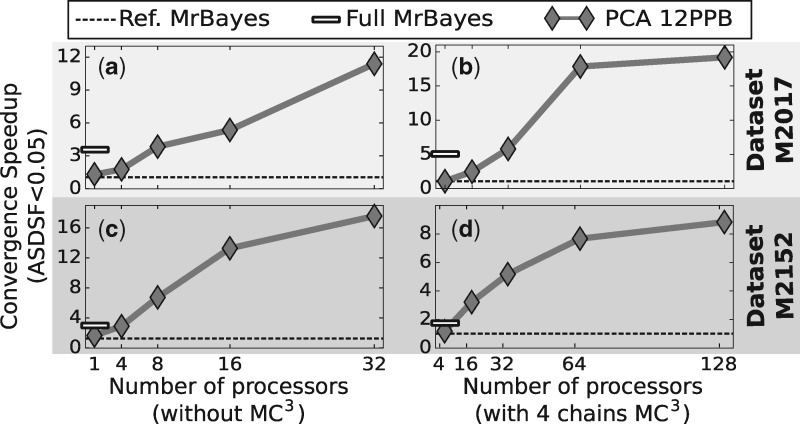
Our framework was finally evaluated on the sampling of the posterior distributions of trees and parameters of the model of nucleotide substitution. At this task, our best method, PCA with 32 processors, was able (Fig. 4) to converge towards the posterior distribution up to 10-20 times faster than its equivalent Ref MrBayes. When compared to the default settings of MrBayes (Full MrBayes) with more advanced tree proposals, our method still showed faster convergence rate as soon as 4–8 processors were used. Against this MrBayes setting, the convergence speedup reached approximately a fourfold factor with 32 processors.

Fig. 4.

Results for the ASDSF convergence speedup comparison with MrBayes when estimating the posterior distribution of the phylogenetic tree and the nucleotide substitution parameters on empiric datasets (TreeBASE M2017 and M2152). (a) and (c) The ASDSF speedup the first, respectively second, datasets for two settings of MrBayes and our PCA method with multiples parameters per block. (c) and (d) illustrate the ASDSF speedup on the same datasets when the previous methods are augmented with PCA

Figure 4a and c illustrate the speedup in ASDSF convergence on datasets M2017 and M2152, respectively, using Ref MrBayes setting without MC³ as reference. Indeed, the Ref MrBayes setting showed similar execution time and convergence performance as our STD variant with updates on one parameter per iteration (see appendix). PCA slightly outperformed Ref MrBayes in the sequential case but was still far from the performance offered by Full MrBayes. However as the number of processors used increased, the performance of PCA exceeded both MrBayes settings. To highlight the versatility of our framework, we applied the same experiment but with MC³ enabled on our framework and MrBayes. Figure 4b and d show the speedup in ASDSF convergence on both datasets with four parallel tempered chains. The trend shown in this second experiment is consistent with our previous results and the speedup of PCA increased with the number of processors used and surpassed the performance of Ref MrBayes and Full MrBayes.

The improvement on convergence rates brought by our framework on this problem is linked with the difficulty of moving through the phylogenetic tree space. Tree proposals are usually suffering from a low acceptance rate and are thus frequently rejected. Indeed, in our experiment, the acceptance rates for tree proposals were lower than 0.05. Such moves are not currently adaptive, but they remain easily predictable and therefore exploitable by the pre-fetching method. While this assumption of low acceptance rate on tree proposals is true for most datasets, it might falter on some of them. To get around this limitation, tree proposals could be made adaptive by tuning the extension probability (e.g. for eSPR) or the proposals on branch lengths that are jointly applied to tree modifications.

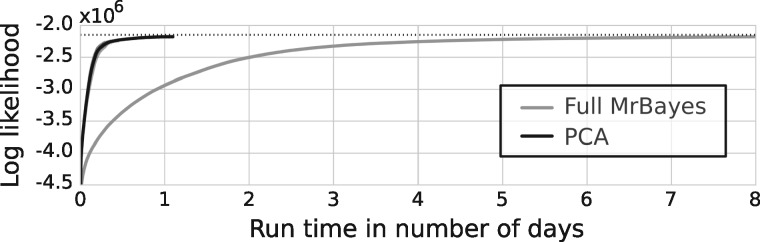
Our results suggest that the approach that we propose has large potentials on more challenging datasets, but the datasets used in previous experiments were easily analyzable using existing software. We therefore used a large dataset representing more than 2800 species with 12 genes of the amphibian family (Pyron and Wiens, 2011) to challenge both Full MrBayes and PCA. For this experiment, we compared four separate runs of Full MrBayes using each four tempered chains with four separate runs of our best method, PCA, with 4 tempered chains having each 32 processors dedicated to our coupling of adaptive MCMC and pre-fetching. While Full MrBayes took more than five days to approach a likelihood plateau (Fig. 5), PCA reached it in less than one day. It is worthwhile to mention that if PCA would be augmented with the advanced tree proposals present in Full MrBayes, further performance gains could be observed.

Fig. 5.

Trace of the log likelihood when estimating the posterior distribution of the phylogenetic tree, branch lengths and nucleotide substitution parameters on an empiric dataset having 2800 species with 12 genes of the amphibian familiy. Average trace and 95% confidence interval are shown for 4 independent runs with of 4 parallel tempered chains of Full MrBayes and PCA with 32 processors

4 Conclusion

Building an efficient MCMC sampler for parameter-rich and complex models is challenging given their inherent expensive computational cost and high parameter-dimension d. Indeed, most of the existing MCMC enhancements may prove inefficient due to their increase in computational effort caused by additional likelihood evaluations or complex operations depending on d ($\mathcal{O}(d^x),x>1$) (e.g. Haario et al., 2005). We presented a M-H framework that overcomes this difficulties by using the coupling of a novel adaptive proposal and pre-fetching. We showed that our new framework improved the mixing, reduced the burn-in phase and speed up the sampling by an order of magnitude when applied to several models of varying complexity including the difficult task of estimating the posterior probability of phylogenetic trees using evolutionary models.

Model dependent enhancements can be used to further improve the performance gain highlighted, as demonstrated by the addition of parallel likelihood computations (Fig. 2b) or MC³ (Fig. 4). Therefore existing evolutionary biology state-of-the-art software, such as MrBayes (Ronquist et al., 2012) or ExaBayes (Aberer et al., 2014), could directly benefit from this framework. Furthermore, since this method is based on speeding up a single M-H process, it could be used as the core of more advanced MCMC methods such as trans-dimensional MCMC (Sisson, 2005) or even Bayes factors computation using thermodynamic integration (Lartillot and Philippe, 2006).

Further capabilities could be built on top of this framework by exploring new approaches such as adaptive tree proposals or an automatic clustering of parameters into optimal blocks. Therefore, beside broadening the range of evolutionary hypothesis tractable using Bayesian inference, our parallel M-H framework provides a potential basis for a new generation of efficient parallel MCMC samplers for parameter-rich models such as those that are currently developed in biological studies.