Comparative Analysis of the Biaxial Mechanical Behavior of Carotid Wall Tissue and Biological and Synthetic Materials Used for Carotid Patch Angioplasty

Abstract

Patch angioplasty is the most common technique used for the performance of carotid endarterectomy. A large number of patching materials are available for use while new materials are being continuously developed. Surprisingly little is known about the mechanical properties of these materials and how these properties compare with those of the carotid artery wall. Mismatch of the mechanical properties can produce mechanical and hemodynamic effects that may compromise the long-term patency of the endarterectomized arterial segment. The aim of this paper was to systematically evaluate and compare the biaxial mechanical behavior of the most commonly used patching materials. We compared PTFE (n = 1), Dacron (n = 2), bovine pericardium (n = 10), autogenous greater saphenous vein (n = 10), and autogenous external jugular vein (n = 9) with the wall of the common carotid artery (n = 18). All patching materials were found to be significantly stiffer than the carotid wall in both the longitudinal and circumferential directions. Synthetic patches demonstrated the most mismatch in stiffness values and vein patches the least mismatch in stiffness values compared to those of the native carotid artery. All biological materials, including the carotid artery, demonstrated substantial nonlinearity, anisotropy, and variability; however, the behavior of biological and biologically-derived patches was both qualitatively and quantitatively different from the behavior of the carotid wall. The majority of carotid arteries tested were stiffer in the circumferential direction, while the opposite anisotropy was observed for all types of vein patches and bovine pericardium. The rates of increase in the nonlinear stiffness over the physiological stress range were also different for the carotid and patching materials. Several carotid wall samples exhibited reverse anisotropy compared to the average behavior of the carotid tissue. A similar characteristic was observed for two of 19 vein patches. The obtained results quantify, for the first time, significant mechanical dissimilarity of the currently available patching materials and the carotid artery. The results can be used as guidance for designing more efficient patches with mechanical properties resembling those of the carotid wall. The presented systematic comparative mechanical analysis of the existing patching materials provides valuable information for patch selection in the daily practice of carotid surgery and can be used in future clinical studies comparing the efficacy of different patches in the performance of carotid endarterectomy.

Introduction

Carotid endarterectomy (CEA) has remained the most common procedure for management of significant carotid stenosis since it was first reported by Eastcott et al. in 1954 [1–3]. The standard approach for the performance of CEA involves a longitudinal arteriotomy from the common to the internal carotid artery followed by removal of the atherosclerotic plaque. There is significant evidence that closing the longitudinal arteriotomy using a patch is superior to primary closure in reducing the risk of restenosis and improving both short and long term clinical outcomes [4–9]. In addition, patches are commonly used to close arteriotomies in other vascular beds, such as after endarterectomy and bypass operations in the lower extremities.

Autologous vein (either greater saphenous or external jugular) was the first material to be used as carotid patch. A vein provides an endothelialized surface to the reconstructed arterial segment, is relatively readily available, easy to handle, and has high resistance to infection. Its disadvantages are the need for an additional incision to obtain it and occasional deterioration with aneurysmal dilatation and rupture. A number of synthetic patches are now available. The advantages of prosthetic patches include immediate availability, avoidance of additional incision, and preservation of the vein for future use in other cardiovascular operations. The shortcomings of the prosthetic patches are higher thrombogenicity and increased risk for infection. Today, a large variety of both synthetic and biological patches are available for the care of patients with carotid disease [3]. The most commonly used materials are synthetic polytetrafluoroethylene (PTFE) and textile Dacron patches, xenogeneic bovine pericardium (BP) and autogenous vein patches including external jugular (EJV) and greater saphenous (GSV) veins.

Among other important characteristics such as impermeability, thromboresistivity, biocompatibility and availability, an ideal carotid patch should have similar mechanical properties to those of the host artery [10–13]. Mismatch in mechanical properties may stimulate local remodeling, compromise patch performance and exacerbate the normal reparative process after endarterectomy causing intimal hyperplasia in the repaired artery [14–18]. Results of several clinical trials have supported this thesis by demonstrating fewer complications and lower restenosis rates for arteries repaired with biological materials, and particularly vein patches, versus synthetic PTFE or Dacron [5, 8, 19–22]. The synthetic patches, however, are still widely used and are the patch of choice among many vascular surgeons.

Substantial progress has been achieved in the study of tissue bio-mechanics [26, 28, 29, 31]. This includes both complex multi-axial experimentation [31, 38, 24] and nonlinear anisotropic constitutive tissue modeling [35, 40, 41]. However, despite its importance, surprisingly little information is currently available on the mechanical behavior of patches used to repair the carotid artery after endarterectomy. Furthermore, experimental studies of the human carotid wall are also rare, with most research being performed using animal tissue. The goal of this study was to perform systematic evaluation and comparison of the biaxial mechanical behavior of different patching materials and the carotid artery wall tissue. Obtained quantitative comparative data may help define the patch of choice among those currently available, but more importantly, can guide changes in the patch construction and characteristics to allow production of a patch with improved mechanical properties.

Materials and Methods

Materials for this study included 18 cadaveric human common carotid artery specimens (CCA), nine samples of external jugular veins (EJV), 10 distal greater saphenous veins (GSV) samples harvested at the ankle, four types of commercially available bovine pericardium (BP) patches (a total of n = 10 specimens: two samples of Synovis VG-0106 N, four samples of Synovis VG-0209 N, two samples of Neovasc PeriPatch N and two samples of Neovasc PeriPatch W2P9) and synthetic Acuseal PTFE (by GORE), Dacron Hemacarotid (by GORE) and Hemashield (by Boston Scientific) patches. Cadaveric carotid tissues were obtained using a protocol approved by the Institutional Review Board of the University of Nebraska Medical Center. Vein specimens were obtained as leftover tissues after carotid endarterectomy and patching following a protocol approved by the Institutional Review Board of Veterans Affairs Nebraska-Western Iowa Medical Center.

Specimen Preparation.

Eighteen cadaveric human CCA specimens (mean age 69 ± 8) approximately 5 cm long and free of gross pathology were harvested within six hours of death using rapid autopsy technique [23–25]. EJVs and GSVs were obtained fresh as leftover materials after carotid endarterectomy. Both carotids and veins were tested within two hours of harvesting.

Prior to testing, arterial and vein specimens were cut longitudinally to release the residual stresses. Veins opened to a completely flat configuration forming a planar sheet of tissue similar to that of the BP and synthetic patches. CCA specimens opened to the initially curved configuration which flattened out under specimens' own weight. Our estimations of resulting bending stresses using the opening angle technique [36] showed that these stresses were small compared to stresses produced by the applied loads.

Square specimens ranging from 7 × 7 mm to 15 × 15 mm in size (depending on the size of the vessel) were then prepared. Initial thickness of the specimen was measured with a Starrett 1010 Z gauge. The samples were attached to the biaxial device using a standard technique [26–28] which utilizes stainless steel hooks and loops of thick surgical nylon suture (see Fig. 1). The hooks were attached to the specimen as close to the edges as possible to minimize the influence of edge effects on the strain field measurements. Four graphite markers were attached to the arterial intima to track the deformations of the specimen. The tests were performed at room temperature in a normal saline bath with the specimen completely immersed.

Fig. 1.

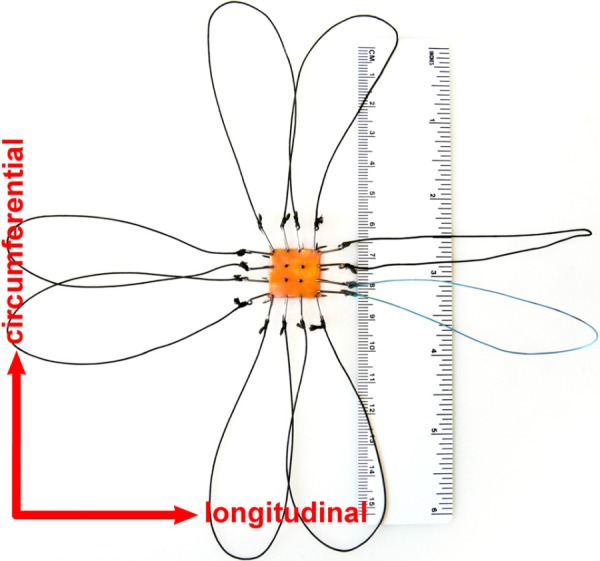
Human CCA specimen prepared for biaxial testing

Biaxial Device Description.

A custom-made soft-tissue biaxial device designed by M. Sacks (see detailed device description in Sacks [26], Grashow [27] and Geest et al. [28, 29]) presented in Fig. 2 was used to study the response of CCA and patching materials in the longitudinal and circumferential directions.

Fig. 2.

CCA specimen attached to the soft-tissue biaxial device. Arrows represent directions of stretch.

The device consists of four translation stages (404XR, Parker Hannafin Corp., Irwin, PA) driven by stepper motors (OS22BSNL10, Parker Hannafin Corp., Irwin, PA). The stages are arranged around the bath that contains the specimen. The spatial resolution for each translation stage is approximately 0.394 μm. The translation stages are equipped with carriage arms which are used for specimen attachment. Each arm is free to rotate about its axis and has a pair of stainless steel pulleys. This allows the applied forces to be equally distributed between all suture lines that hold the specimen.

Deformations of the specimen were measured by tracking the movements of the four graphite markers with a video camera (Sony XCD-X700). In-plane stretch and shear angle were calculated during the test from marker displacements using a four-node finite element technique [26, 27]. The applied loads were measured with a pair of tension/compression 250 g load cells (Honeywell Sensotec). These load cells were selected to cover the estimated physiological loads in the artery (see details below in the Tissue Anisotropy section). The entire setup was placed on a vibration isolation tabletop to minimize the vibration caused by stage movements.

Test Protocol.

Prior to testing, standard weight measures were used to calibrate the load cells and confirm their linearity. Test protocol was load controlled and each specimen was loaded equibiaxially (same load was applied in both longitudinal and circumferential directions). Cyclic preloading of all specimens was used to eliminate the effects of stress-softening and obtain elastic response [30]. To ensure consistency from sample to sample, all loading cycles were initiated at a tare load of 4.9 × 10⁻³ N (0.5 g) and all presented stretch data were referenced to the preconditioned tare configuration. Ten cycles of repeatable loading and unloading were applied after which Engineering-stress-stretch response was recorded. We note that most specimens were preconditioned after only two to three cycles. Hysteresis between the loading and unloading stress-stretch curves that represents energy loss during deformation was small for most specimens. Therefore only stress-stretch curves that correspond to loading are given further. Loading rate effect was evaluated and it was found that varying the time required to load the specimen in the range from 30 s to 1 s showed little to no difference in the stress-stretch curves. Data presented below were obtained during 30 s cycle. For all specimens, shear angle calculated according to Sacks and Chuong [31] did not exceed 3° and the influence of shear was negligible.

Tissue Anisotropy.

The degree of material anisotropy can be characterized by the ratio of tangent elastic moduli along the two directions of stretch [31]. For nonlinear materials, such as those presented here, the elastic moduli are not constant; therefore, anisotropy ratio should be evaluated at certain levels of stress. These levels were estimated considering an average CCA with diameter of 8 mm and wall thickness of 0.8 mm under internal pressures of 60 mm Hg (end diastolic), 120 mm Hg (normal peak systolic) and 160 mm Hg (stage II hypertension peak systolic). According to Laplace's law (σ_θθ = Pd/2h) and assuming that the arterial wall is thin, these values of pressure correspond to 40 kPa, 80 kPa and 110 kPa levels of average Cauchy circumferential stress in the arterial wall. These levels of stress were selected for calculation of anisotropy indexes A₄₀, A₈₀ and A₁₁₀ as the difference between tangent elastic moduli along the longitudinal and circumferential directions divided by the average tangent elastic modulus [18]. This definition of anisotropy index was chosen versus the simple ratio of moduli due to its symmetry in describing materials with reverse anisotropy.

Since tangent elastic moduli characterize the nonlinear material behavior only at a particular state of deformation, we have also defined an additional anisotropy index A_int to characterize the “cumulative” anisotropy. This anisotropy index A_int was introduced to show the difference between the stress-stretch curves obtained for the two directions of stretch and it was defined as the difference of areas bound between each of these curves and the vertical (stress) axis divided by the average area. Practical calculation of anisotropy index A_int involved numeric integration of stress-stretch data with respect to stress in the interval from zero to 110 kPa. We note that even though integration with respect to strain would have been more conventional, we chose to perform integration with respect to stress because integration over strain would have resulted in a shorter integration base under the stress-controlled conditions and therefore would have complicated the integral anisotropy comparisons. Integration was performed for longitudinal and circumferential graphs separately. Index A_int is positive if the longitudinal direction is stiffer than the circumferential and negative in the opposite case. For isotropic materials, these two curves coincide and the index A_int = 0.

Results

Common Carotid Artery Specimens.

The equibiaxial mechanical responses in the longitudinal and circumferential directions of 18 tested CCA specimens are presented in Fig. 3. We found that the CCA tissue is highly nonlinear and anisotropic and can undergo considerable stretch. Under maximum load the observed stretches were in the range of 1.116‐1.387 for longitudinal and 1.085‐1.305 for circumferential directions. Stress-stretch curves show considerable increase in arterial stiffness with increasing load. The mechanical properties of the CCA were quite variable between specimens.

Fig. 3.

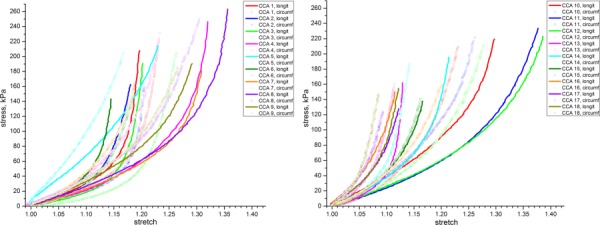
Equibiaxial stress-stretch response of CCA specimens in longitudinal and circumferential directions. Graphs were separated into two plots for better visualization.

From 18 tested specimens, 13 were stiffer in the circumferential direction while five were stiffer in the longitudinal direction. As seen in Fig. 3, the anisotropy of the tested CCAs is substantial. Tangent elastic moduli and their inter-specimen variability for three levels of stress (40 kPa, 80 kPa and 110 kPa) are presented in Fig. 4. Anisotropy indexes A₄₀, A₈₀, A₁₁₀, A_int and their inter-specimen variations are presented in Table 1 and Figs. 5 and 6. Values of tangent elastic moduli increased with increasing stress level, which demonstrates the stiffening effect of arteries under increased loads (p < 0.05). In particular, stress levels corresponding to stresses associated with stage II hypertension (110 kPa level) caused an increase in CCA tangent elastic moduli of 1.5-fold comparing to those at stresses corresponding to the ones associated with normal systolic blood pressure (80 kPa level) and more than 3-fold comparing to end diastolic pressure (40 kPa). The inter-specimen variability of the calculated stiffness values also increased with stress. Of interest, anisotropy index A₁₁₀ was closer to zero than indexes A₈₀ and A₄₀ which indicates that tested CCAs were more anisotropic at low stresses than at high stresses. The majority of the CCA specimens were stiffer in the circumferential direction than in the longitudinal (p = 0.06), which resulted in higher elastic moduli in this direction and negative values of anisotropy indexes.

Fig. 4.

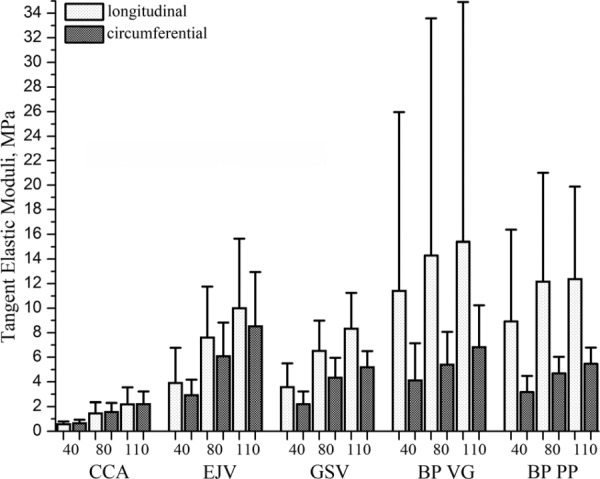
Values and range of tangent elastic moduli in longitudinal and circumferential directions calculated for 40 kPa, 80 kPa and 110 kPa levels of stress for common carotid arteries (CCA), external jugular veins (EJV), greater saphenous veins (GSV) and two types of bovine pericardium (BP) patches (Synovis VG and Neovasc PP)

Table 1.

Anisotropy Indexes A₄₀, A₈₀, A₁₁₀, A_int for Common Carotid Artery Specimens

Common Carotid Artery
No	A40	A80	A110	Aint	No	A40	A80	A110	Aint
1	0.09	0.19	0.43	0.13	11	−0.37	−0.41	−0.25	−0.39
2	0.35	−0.31	−0.46	0.21	12	−0.32	−0.52	−0.47	−0.20
3	0.04	0.32	0.37	0.24	13	−0.06	0.40	0.50	−0.30
4	−0.24	−0.32	−0.23	−0.36	14	−0.53	−0.84	−0.67	−0.29
5	−0.31	−0.23	−0.24	−0.31	15	−0.08	0.00	−0.16	−0.01
6	0.04	0.37	0.67	0.21	16	0.40	0.34	0.45	0.56
7	−0.41	−0.41	−0.38	−0.51	17	−0.29	−0.27	−0.25	−0.25
8	−0.21	−0.30	−0.22	−0.21	18	−0.40	−0.29	−0.22	−0.32
9	−0.08	−0.13	−0.12	−0.08	Mean	−0.15 ± 0.26	−0.17 ± 0.36	−0.1 ± 0.40	−0.11 ± 0.28
10	−0.38	−0.59	−0.59	−0.08

Fig. 5.

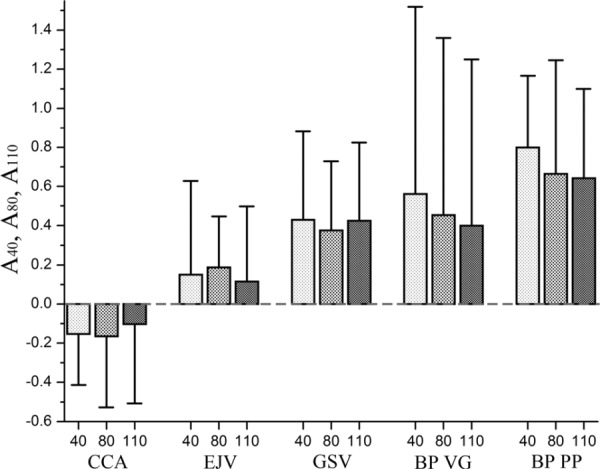
Anisotropy indexes A₄₀, A₈₀, A₁₁₀ and their variations calculated for 40 kPa, 80 kPa and 110 kPa levels of stress respectively for common carotid arteries (CCA), external jugular veins (EJV), greater saphenous veins (GSV) and two types of bovine pericardium (BP) patches (Synovis VG and Neovasc PP)

Fig. 6.

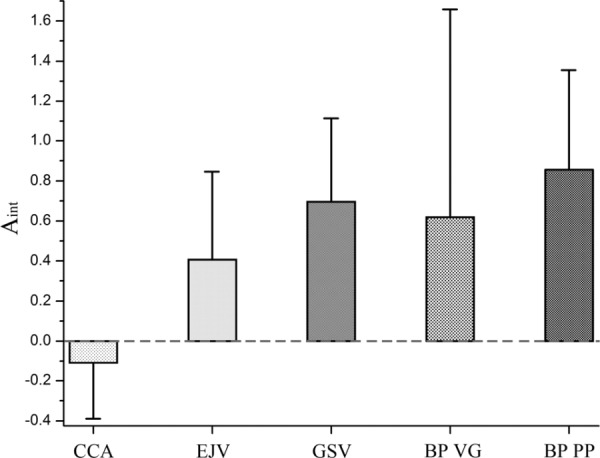
Anisotropy index A_int and its variability calculated for common carotid arteries (CCA), external jugular veins (EJV), greater saphenous veins (GSV) and two types of bovine pericardium (BP) patches (Synovis VG and Neovasc PP)

Vein Patches.

The equibiaxial stress-stretch response in the longitudinal and circumferential directions of nine human EJVs is presented in Fig. 7. Similar to carotid specimens, EJVs exhibited substantial nonlinearity and anisotropy. However, the shape of the stress-stretch curves for the EJV is qualitatively different from those of the carotid. The stiffness of most veins under small loads is significantly smaller than that of the carotids which causes veins to deform substantially until a particular stretch value is reached. Up to this point, the graph is almost parallel to the stretch axis (toe region), indicating very low resistance of the vein to the applied load. However, after passing this stretch value, the stiffness of the vein increases dramatically and the vein is not able to deform much further even when significant loads are applied. We note that several tested specimens did not have the toe region (such as specimen 8 on Fig. 7) which resulted in fast increase of vein stiffness.

Fig. 7.

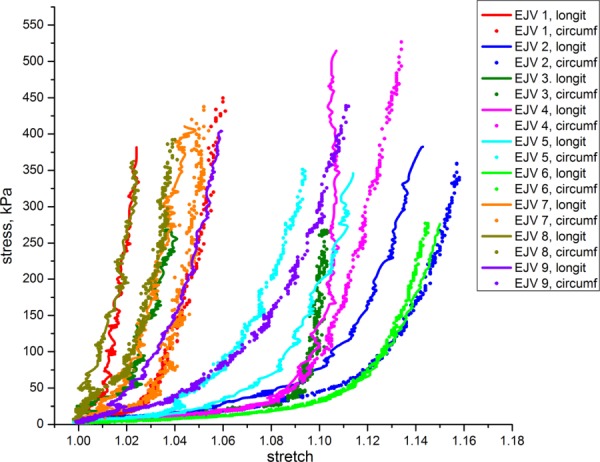
Equibiaxial stress-stretch response of EJV specimens in longitudinal and circumferential directions

Seven EJV specimens were stiffer in the longitudinal direction and two in circumferential. From these two, one specimen was near isotropic. This result is opposite to what was observed in CCA specimens. EJVs showed substantial variability in their mechanical properties among different patients and a broad range of stretches (1.026–1.152 for the longitudinal direction and 1.041–1.159 for the circumferential direction). The range of stretches, however, was smaller than that of the carotids.

The equibiaxial responses of 10 human GSVs are presented in Fig. 8. Similar to our findings with EJV, the GSV undergoes substantial deformation under small loads with later dramatic increase in stiffness. All GSV specimens were stiffer in the longitudinal direction than in the circumferential.

Fig. 8.

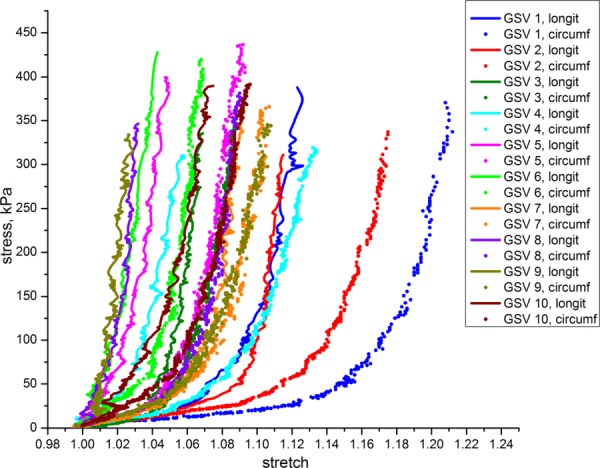
Equibiaxial stress-stretch response of GSV specimens in longitudinal and circumferential directions

Tangent elastic moduli and their inter-specimen variability for EJV and GSV specimens are presented in Fig. 4. Anisotropy indexes A₄₀, A₈₀, A₁₁₀, A_int are presented in Table 2 and Figs. 5–6. Similar to carotids, veins demonstrated increased stiffness under increasing load which resulted in the increase of the tangent elastic moduli along both directions of stretch. Namely, tangent elastic moduli of veins at 110 kPa stress level were on average more than 1.3-fold larger comparing to 80 kPa level and more than 2.5-fold lager comparing to 40 kPa stress level. Mean elastic moduli of the EJV were higher than those of the GSV for all three considered stress levels. However, GSV showed higher anisotropy compared to EJV. Similar to carotids, veins demonstrated higher anisotropy at small loads compared to high loads. Anisotropy indexes for veins were positive, reflecting the observation that the majority of EJVs and all GSVs were stiffer in the longitudinal direction than in the circumferential (p < 0.05). EJV demonstrated broader range of longitudinal stretches, but more narrow range of circumferential stretches compared to GSV. GSV maximum stretches varied between 1.030–1.134 for longitudinal and 1.070–1.213 for circumferential directions. Of interest, GSVs showed higher variability in mechanical properties among different patients than EJVs.

Table 2.

Anisotropy Indexes A₄₀; A₈₀; A₁₁₀; A_int for Vein Specimens (EJV and GSV)

External Jugular Vein
No	A40	A80	A110		Aint
1	0.67	0.67	0.95		0.96
2	−0.13	−0.15	−0.04		0.21
3	−0.26	−0.13	−0.29		0.90
4	0.11	0.19	0.33		0.08
5	−0.58	0.10	−0.10		−0.31
6	−0.04	0.16	−0.20		−0.02
7	0.11	0.10	−0.10		0.49
8	0.59	0.35	0.11		0.65
9	0.89	0.40	0.36		0.69
Mean	0.15 ± 0.48	0.19 ± 0.26	0.11 ± 0.38		0.41 ± 0.44
Greater Saphenous Vein
No	A40	A80	A110	Aint
1	0.11	0.08	−0.10	0.65
2	0.31	1.00	0.82	0.34
3	0.00	0.18	0.33	0.20
4	0.53	0.59	0.53	0.96
5	−0.22	0.40	0.15	0.89
6	0.80	0.29	0.33	0.87
7	0.13	0.00	0.50	0.11
8	0.55	0.67	0.67	1.18
9	1.27	0.67	1.14	1.34
10	0.82	−0.12	−0.15	0.41
Mean	0.43 ± 0.45	0.38 ± 0.35	0.42 ± 0.40	0.70 ± 0.42

Bovine Pericardium.

The equibiaxial responses of 10 commercial BP patches in both longitudinal and circumferential directions are presented in Fig. 9. BP patches were divided into two groups by their manufacturer to avoid possible systematic influence of proprietary patch preparation techniques (BP patches undergo cross-linking) on their mechanical properties. Similar to other tissues tested in this study, BP showed substantial nonlinearity, anisotropy, and variability among different patches, even patches with the same catalog name. Scattering of mechanical properties for BP specimens was somewhat expected and is due to an individually specific underlying structure of the animal tissue. Bovine pericardium does not have expressly defined natural longitudinal and/or circumferential direction. However, all BP-derived commercial cardiovascular patches have elongated strip shape with recommended longitudinal and circumferential axes. We therefore kept the names longitudinal and circumferential in our data analysis. In four Synovis VG patches and all Neovasc PP patches, the longitudinal direction was stiffer than the circumferential (similar to veins). In two Synovis VG specimens, the circumferential direction was stiffer than the longitudinal (similar to CCA). Of interest, for several BP specimens (see Table 3) the difference between the longitudinal and circumferential directions was quite substantial which resulted in large values of anisotropy indexes. The mean anisotropy indexes for both types of BP patches were positive (p < 0.05) which is opposite to what was obtained for the CCAs. Maximum stretches observed in BP specimens were three to four times smaller than those seen in CCA under the same loads. Namely, the range of maximum stretches for BP was 1.006–1.093 for the longitudinal direction and 1.034–1.112 for the circumferential direction.

Fig. 9.

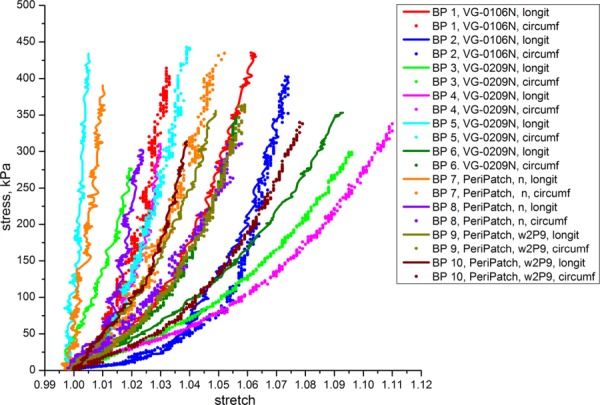
Equibiaxial stress-stretch response of commercially available BP in longitudinal and circumferential directions

Table 3.

Anisotropy Indexes A₄₀, A₈₀, A₁₁₀, A_int for Bovine Pericardium Specimens (Synovis VG and Neovasc PP)

Bovine Pericardium Synovis VG
No	A40	A80	A110	Aint
1	−0.889	−0.615	−0.333	−0.68
2	0.519	0.000	−0.194	0.14
3	1.500	1.200	1.111	1.63
4	1.152	1.077	0.980	1.04
5	1.333	1.478	1.385	1.84
6	−0.250	−0.419	−0.560	−0.26
Mean	0.56 ± 0.96	0.45 ± 0.91	0.40 ± 0.85	0.62 ± 1.04
Bovine Pericardium Neovasc PeriPatch
No	A40	A80	A110	Aint
1	1.200	1.097	1.000	1.56
2	0.857	1.231	1.048	0.66
3	0.311	0.118	0.105	0.39
4	0.828	0.211	0.410	0.81
Mean	0.80 ± 0.37	0.66 ± 0.58	0.64 ± 0.46	0.85 ± 0.50

BP demonstrated the highest scatter of elastic moduli among all tested materials. Of interest, scatter was substantially higher in the longitudinal direction than in the circumferential (see Fig. 4). Similar to carotids and veins, stiffness of the BP patches increased and anisotropy decreased under higher loads (see Fig. 5).

Synthetic (PTFE and Dacron) Patches.

The synthetic patches tested included Acuseal PTFE and two types of Dacron patches:-knitted polyester Hemacarotid and knitted Hemashield. The equibiaxial responses of synthetic patches are presented in Fig. 10. Our data show that all synthetic patches are very stiff in both directions of stretch (>15-fold stiffer than carotid artery wall). In addition, the behavior of PTFE and textile patches is very similar in the two directions and the deformation behavior is almost linear in the applied load range. This result is somewhat unexpected for textile patches, since their knitted structure implies anisotropy. Dacron Hemacarotid and Hemashield patches have special markings indicating their longitudinal direction and the recommended orientation for suturing the patch to the host artery. Nevertheless, the values of the anisotropy indexes for the tested synthetic patches were close to zero. Tangent elastic moduli for Acuseal PTFE, knitted Hemacarotid and knitted Hemashield patches were 27 MPa, 28 MPa, and 40 MPa, respectively.

Fig. 10.

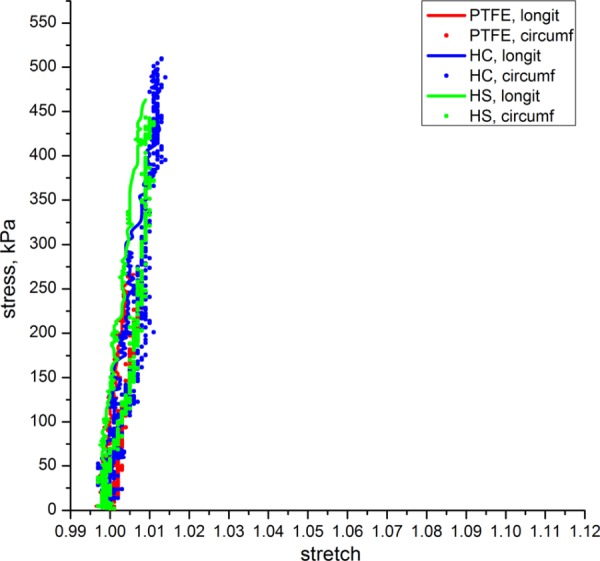
Equibiaxial stress-stretch response of commercially available synthetic patches: Acuseal polytetrafluoroethylene (PTFE), knitted Hemacarotid (HC) and knitted Hemashield (HS) patches

Analysis and Discussion

Common Carotid Artery.

Data on the mechanical properties of the CCA are rather limited in the literature. Most of the previous studies evaluated arteries obtained from animals (usually dogs) [25, 32–35]. Few studies were performed on human tissues [16, 36–39]. However, these were either done using a uniaxial experimental setup or were performed on tubular specimens. The latter implies the presence of residual stresses.

Our results show substantial nonlinearity in the stress-stretch response characterized by exponential increase in stiffness for all CCA specimens. This phenomenon is well-known for cardiovascular tissue [35, 36, 38, 40] and can be explained by the structure of the arterial wall which is a multilayered composite. Among other components, it contains fibers of collagen and elastin. When the artery is load-free, stiff collagen fibers are wrinkled and the response of the vessel is determined largely by weak elastin. When the artery is being stretched, collagen fibers straighten out and the overall stiffness of the tissue dramatically increases, which results in the observed stress-stretch response. In addition to nonlinearity, CCA specimens demonstrated appreciable anisotropy with most specimens being stiffer in the circumferential direction than in the longitudinal. Interestingly, for several carotid artery specimens, the anisotropy was reversed. Most specimens exhibited higher anisotropy at smaller stress levels. Anisotropy of the carotid artery has been reported previously [35, 37–39]. Similar to nonlinearity, the observed anisotropy is related to the internal structure of the arterial wall. Collagen fibers inside the tissue form two helically arranged families [40, 41]. The angle of orientation as well as volume fraction of fibers and their stiffness contribute substantially to the anisotropic response observed in the experimental stress-stretch curves. It is well-known that biological tissues can remodel with time to accommodate the local stress levels and other physiological conditions. This may be partly responsible for the observed substantial patient-to-patient variability. More studies are needed to understand the relation between carotid tissue structure, its anisotropic response, and localized loading conditions; however, our results present first evidence of possible “reverse” anisotropy in the carotid tissue wall. Our data also demonstrate large variability among CCA specimens and substantial range of maximum stretches. This finding is in agreement with previously reported data by our group [16] and others [38, 39].

Synthetic Patches.

The behavior of the patching materials was studied using the same biaxial testing technique as was applied to CCA. The synthetic patches, including Acuseal PTFE, textile Hemacarotid and textile Hemashield, were substantially stiffer than the carotid wall. In addition, their behavior was almost linear in the applied load range. The observed substantial stiffness of the PTFE patch is in agreement with work published previously by our and other groups [16, 42–45]. We have not found data on the mechanical properties of carotid Dacron patches in the literature. However, results obtained by other groups reporting on the mechanical properties of Dacron grafts used for aortic replacement or bypass [18, 44, 46] seem to contradict our findings and describe much larger deformations of these grafts in the longitudinal direction. We note that unlike aortic Dacron grafts that are crimped in the longitudinal direction (which allows the cylindrical graft to stretch longitudinally and bend without global buckling), carotid patches are flat (not crimped). The substantial reported stiffness of the aortic Dacron grafts in the non-crimped circumferential direction [18, 44, 46] is in agreement with our data.

Bovine Pericardium Patches.

Similar to synthetic patches, commercial BP patches are readily available. Compared to synthetic patches, BPs show comparable efficacy but may have a lower incidence of recurrent stenosis [3, 47, 48]. Our results from testing several commercially available BP patches showed substantial nonlinearity, anisotropy and variability among different specimens even of the same manufacturer. In the majority of specimens, the longitudinal direction was stiffer than the circumferential (see definitions above), which is opposite to what was observed in CCA specimens. Maximum stretches registered for BP patches were three to four times smaller than those seen in CCA under the same load which demonstrates increased stiffness for the BP compared to the CCA wall. The observed high anisotropy of BP is in agreement with the findings of Sacks et al. [31], but contradicts findings reported by Tremblay et al. [18] and Lee et al. [49]. The latter groups reported almost isotropic properties of glutaraldehyde treated BP specimens. However, BP tissue contains collagen fibers oriented in certain directions [31]. Its structure therefore can support anisotropy. No information is currently available on the methods of harvesting and processing of the pericardial sac. In addition, less clear are the methods followed for patch location and orientation within the BP sack, or details on tissue processing during patch manufacturing that could explain the observed patch variability. However, the presented results show that all BP patches are significantly stiffer than the CCA.

Vein Patches.

Patching with autologous venous tissue remains the most commonly used option for closing the arteriotomy after carotid endarterectomy [3]. The veins most commonly used are the GSV and EJV [50]. GSV is harvested from the patient's thigh or ankle which requires a separate incision and therefore causes additional trauma to the patient. EJV does not require a separate incision, but is substantially thinner than GSV, which raises concerns of this patch becoming aneurysmal with subsequent complications related to thrombosis or rupture. Such vein ruptures when occurring have been associated with high rates of death or severe disability of the patient [51]. To avoid rupture or aneurysmal expansion, some surgeons use the EJV in a double-walled configuration. Our data show that of all patch materials tested, vein patches have the closest mechanical properties to those of the CCA, which nevertheless are still quite different. Similar to CCA specimens, veins exhibited substantial nonlinearity and anisotropy. However their behavior was both qualitatively and quantitatively different. Under small loads, veins were very compliant; however, after reaching a certain limit, they gained stiffness exponentially fast and were not stretching any longer. Similar effect was noticed previously by Wesly et al. [52]. The majority of EJVs and all GSVs were stiffer in the longitudinal direction than in circumferential. This is opposite to what was observed for the CCA. Anisotropy of GSVs is substantially larger than the one of the carotid arteries; but similar to CCAs veins demonstrated higher anisotropy under smaller loads. Both types of veins were stiffer than CCA everywhere except under very small loads. GSV comes closer to the range of the CCA response in circumferential direction, but EJV is somewhat closer to the CCA in the longitudinal direction.

Comparison of Mean Properties and Analysis of Scatter.

Patching materials and carotid artery tissue were compared by calculating the mean stress-stretch responses along with standard deviations. Mean graphs are plotted in Fig. 11. Ranges of standard deviations are plotted separately in Fig. 12. Mean anisotropy indexes for the tested biological materials are presented in Figs. 5 and 6.

Fig. 11.

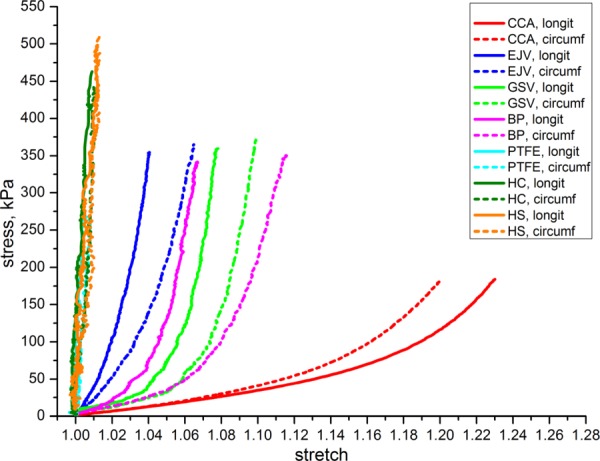
Mean stress-stretch curves calculated for all types of materials tested

Fig. 12.

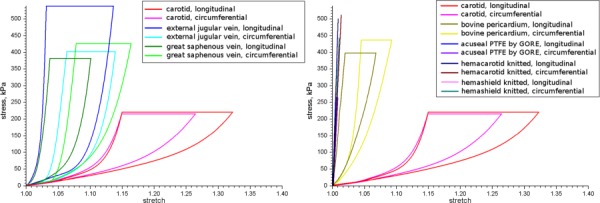
Standard deviations (plotted as mean and one standard deviation in each direction) of mechanical properties of the human CCAs and materials used as patches during carotid endarterectomy. Data are presented for two directions of stretch – longitudinal and circumferential.

Our results show that none of the tested patching materials matches the stress-stretch response of the carotid artery wall even taking into account statistical variability. All patches were stiffer than the artery in both longitudinal and circumferential directions. The patches with properties closer to those of the carotid wall are the GSV (> 3-fold stiffer than CCA) and EJV (> 4-fold stiffer than CCA), followed by BP (> 4.5-fold stiffer than CCA). Synthetic PTFE and Dacron patches had the properties that were the most different from the CCA (>15-fold stiffer than CCA). On average, CCA tissue was stiffer in the circumferential direction than in the longitudinal. However, the opposite was observed for both types of vein patches and BP.

Substantial stiffness of patches compared to the host artery may produce concentration of stresses in the vessel wall adjacent to the anastomosis [15, 16]. These, in turn, can result in development of intimal hyperplasia, disruption of the suture-line and formation of false aneurysm [14, 53, 54] which can eventually result in a variety of complications including stenosis of the vessel, local hemorrhage or thrombosis, distal embolization and stroke, compromising the value of the implanted patch [15, 55].

All tested biological materials demonstrated substantial scatter (see Fig. 12). The largest deviations of stretch were observed for CCA specimens, while the lowest (but still substantial) were registered for BP patches. Interestingly, for CCA and EJV variability was higher in the longitudinal direction, while GSV varied more in the circumferential direction.

Conclusions

Our data point to several important conclusions. First, none of the existing patching materials matches the mechanical response of the carotid artery wall; therefore, there is considerable room for improvement. Even though all tested patches were significantly stiffer in both longitudinal and circumferential directions than the CCA, the closest response was observed for vein patches. This response was nevertheless still quite different than the one of the carotid artery wall. Synthetic materials were the stiffest and therefore mechanically the least favorable to be used as carotid patches.

Second, all tested biological materials have demonstrated significant anisotropy in their mechanical properties. The majority of carotid artery specimens were stiffer in the circumferential direction than in the longitudinal. Vein patches and bovine pericardium have demonstrated the opposite result with the longitudinal direction being stiffer than the circumferential. This is important to consider when using patch materials to repair arterial defects. Opposite anisotropy can compound the effects from the mismatch in mechanical properties between the patch and the host artery. Although it is not practical for vein patches, different patch material orientation might be considered for bovine pericardium.

The outcomes of the present analysis can be used by surgeons to select the patch of choice among those currently available for the care of their patients undergoing carotid endarterectomy operations. Our results can also guide efforts on the development of new types of patches using tissue engineering and other methods [37,56–60]. The large variability of the native carotid tissue documented in this work (with individual specimen loading curves and calculated anisotropy indices) raises the possibility of development of individualized patches that will be tailored to match tissue properties for a specific patient. Finally, mismatch of the average patch and carotid properties may be taken into account while evaluating the efficacy of different patches in clinical trials.