Working Memory Load Strengthens Reward Prediction Errors

Abstract

Reinforcement learning (RL) in simple instrumental tasks is usually modeled as a monolithic process in which reward prediction errors (RPEs) are used to update expected values of choice options. This modeling ignores the different contributions of different memory and decision-making systems thought to contribute even to simple learning. In an fMRI experiment, we investigated how working memory (WM) and incremental RL processes interact to guide human learning. WM load was manipulated by varying the number of stimuli to be learned across blocks. Behavioral results and computational modeling confirmed that learning was best explained as a mixture of two mechanisms: a fast, capacity-limited, and delay-sensitive WM process together with slower RL. Model-based analysis of fMRI data showed that striatum and lateral prefrontal cortex were sensitive to RPE, as shown previously, but, critically, these signals were reduced when the learning problem was within capacity of WM. The degree of this neural interaction related to individual differences in the use of WM to guide behavioral learning. These results indicate that the two systems do not process information independently, but rather interact during learning.

SIGNIFICANCE STATEMENT Reinforcement learning (RL) theory has been remarkably productive at improving our understanding of instrumental learning as well as dopaminergic and striatal network function across many mammalian species. However, this neural network is only one contributor to human learning and other mechanisms such as prefrontal cortex working memory also play a key role. Our results also show that these other players interact with the dopaminergic RL system, interfering with its key computation of reward prediction errors.

Introduction

Reinforcement learning (RL) theory (Sutton and Barto, 1998) proposes that we can learn the value associated with various choices by computing the discrepancy between the reward that we obtain and our previously estimated value and proportionally adjusting our estimate. This discrepancy, the reward prediction error (RPE), signals a valenced surprise at the outcome being better or worse than expected and a direction to adapt behavior (Daw and Doya, 2006; Pessiglione et al., 2006; Schönberg et al., 2007). In the brain, corticobasal ganglia loops appear to implement a form of algorithmic RL: dopamine-dependent plasticity in the striatum may reinforce selection of choices leading to positive RPEs and weaken those leading to negative RPEs (Frank et al., 2004; Collins and Frank, 2014). Dopaminergic neurons exhibit phasic changes in their spike rates that convey RPEs (Montague et al., 1996; Schultz, 2002) and dopamine release in target regions provides a bidirectional RPE signal (Hart et al., 2014). Human imaging studies have indeed found that striatal BOLD correlates with RPE and is enhanced by dopamine manipulations (Pessiglione et al., 2006; Schönberg et al., 2007; Jocham et al., 2011).

However, other neurocognitive processes contribute to learning in addition to the integration of reward history by RL. Specifically, executive processes (such as those involved in representing sequential or hierarchical task structure) contribute substantially to human learning over and above incremental RL (Botvinick et al., 2009; Badre and Frank, 2011; Daw et al., 2011; Collins and Koechlin, 2012; Collins and Frank, 2013). Even in basic stimulus–response learning tasks, working memory (WM) contributes substantially to instrumental learning beyond RL (Collins and Frank, 2012; Collins et al., 2014), as evidenced by both behavioral analyses and quantitative computational model fits. Two effects of WM were evident in learning. As WM set size increased (WM load), learning curves per stimulus were slowed. Second, accuracy per trial declined as a function of the number of intervening items (WM delay). These WM effects decayed with further experience as the more reliable but slower RL process gained control of behavior. A hybrid model of WM and RL provided a better fit to these data than either process alone (Collins and Frank, 2012; Collins et al., 2014).

This prior behavioral work implies that WM contributes to RL processes. Here, we investigate the neural markers of learning and RPEs to determine whether they are interact with WM. Although many RL studies have revealed neural correlates of RPEs that relate to learning, these studies have not manipulated or estimated WM factors that could contribute to (and potentially confound) these signals. Identifying separate markers of systems that contribute jointly to behavior also provides an opportunity to explore whether they interact (e.g., competitively or cooperatively). Specifically, we tested whether frontoparietal networks associated with cognitive control and striatal systems associated with RL would show parametric modulations of RPE signaling as a function of WM load during learning. We also tested whether such interactions would be predictive of the extent to which individuals relied on WM contributions to RL behaviorally.

Materials and Methods

Participants

We scanned 26 participants (age 18–31 years, mean 23, 15 males/11 females). All 26 participants are included in the behavioral analysis. Five participants were excluded from fMRI analysis before analyzing their fMRI data due to head movement greater than our voxel size. Two to six blocks were excluded from three other participants due to movement during data collection toward the end of the scan. All participants were right-handed with normal or corrected-to-normal vision and were screened for the presence of psychiatric or neurological conditions and contraindications for fMRI. All participants were compensated for their participation and gave informed, written consent as approved by the Human Research Protection Office of Brown University.

Experimental design

The task (Fig 1) was similar to that described previously (Collins and Frank, 2012; Collins et al., 2014), itself adapted from a classic conditional associative learning paradigm (Petrides, 1985). On each trial, subjects had to respond with one of three responses (button presses on a response pad) when presented with a centrally displayed single stimulus. Subjects had to learn over trials which response was correct for each stimulus based on binary deterministic reinforcement feedback (Collins and Frank, 2012; Collins et al., 2014).

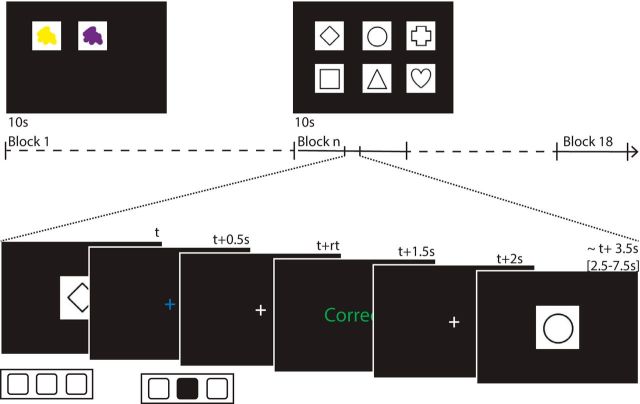
Figure 1.

Experimental protocol. At the beginning of each block, subjects were shown for 10 s the set of stimuli they would see in that block. In this example, Block 1 uses color patches for stimuli and has a set size n_s = 2; Block n uses shapes and has n_s = 6. Each trial included the presentation of a stimulus for 0.5 s, followed by a blue fixation cross until subject pressed 1 of 3 buttons or up to 1.5 s after trial onset. Button press caused the fixation cross to turn white. Feedback was presented for 1 s and came 1.5 s after trial onset. Feedback consisted of the words “correct” or “incorrect” in green and red, respectively. The intertrial interval consisted of a white fixation cross with jittered duration to allow trial-by-trial event-related analysis of fMRI signal. Blocks set sizes varied between one and six and the order was randomized across subjects.

To manipulate WM demands separately from RL components, we varied the number of stimuli (denoted as set size n_s) to be learned within a block systematically. Larger set sizes provide greater load on WM and also impose on average larger delays between repetitions of the same stimulus. Subjects experienced three blocks of each of the set sizes one through six. In each block, subjects learned about a different category of visual stimulus (e.g., sports, fruits, places, etc.), with stimulus category assignment to block set size counterbalanced across subjects. Block ordering was also counterbalanced within subjects to ensure an even distribution of high/low load blocks across each third of the experiment.

At the beginning of each block, subjects were shown the entire set of stimuli for that block and were encouraged to familiarize themselves with them for a duration of 10 s (Fig. 1, top). They were then asked to make their response as quickly and accurately as possible after each individual stimulus presentation. Within each block, stimuli were presented 12 times, each in a pseudorandomly intermixed order.

Stimuli were presented in the center of the screen for up to 0.5 s, followed by a blue fixation cross for up to 1 s or subjects making a choice by pressing 1 of 3 buttons, at which time the fixation cross turned white (Fig. 1, bottom). Feedback was presented 1.5 s after stimulus onset for 0.5 s as either “correct” in green, “incorrect” in red, or “too slow” if the subject failed to answer within 1.5 s. A white fixation cross followed with jittered duration of mean 1.5 s (range 0.5–6.5 s) before the next stimulus was presented.

Subjects were instructed that finding the correct action for one stimulus was not informative about the correct action for another stimulus. This was enforced in the choice of correct actions, such that, in a block with e.g., n_s = 3, the correct actions for the three stimuli were not necessarily three distinct keys. This procedure was implemented to ensure independent learning of all stimuli (i.e., to prevent subjects from inferring the correct actions to stimuli based on knowing the actions for other stimuli). Before entering the scanner, subjects went through the instructions and practiced on a separate set size two sets of images to ensure that they were familiarized with the task.

Computational model

RLWM model

To better account for subjects' behavior and to disentangle the roles of WM and RL, we fitted subjects' choices with our hybrid RLWM computational model. Previous research showed that this model, which allows choice to be a mixture between a classic delta rule RL process and a fast but capacity-limited and delay-sensitive WM process, provided a better quantitative fit to learning data than models of either WM or RL alone (Collins and Frank, 2012; Collins et al., 2014). The model used here is a variant of the previously published models. We first summarize its key properties and then follow up with the details.

RLWM includes two modules that separately learn the value of stimulus–response mappings: a standard incremental procedural RL module with learning rate α and a WM module that updates S-R-O associations in a single trial (learning rate 1) but is capacity limited (with capacity K). The final action choice is determined as a weighted average over the two modules' policies. How much weight is given to WM relative to RL (the mixture parameter) is dynamic and reflects the probability that a subject would use WM versus RL in guiding their choice. This weight depends on two factors. First, a constraint factor reflects the a priori probability that the item is stored in WM, which depends on set size n_s of the current block relative to capacity K (i.e., if n_s > K, then the probability that an item is stored is K/n_s) scaled by the subject's overall reliance of WM versus RL (factor 0 < ρ < 1), with higher values reflecting relative greater confidence in WM function. Therefore, the constraint factors indicates that the maximal use of WM policy relative to RL policy is w₀ = ρ × min(1, K/n_s). Second, a strategic factor reflects the inferred reliability of the WM compared with RL modules over time: initially, the WM module is more successful at predicting outcomes than the RL module, but because it has higher capacity and less vulnerability to delay, the RL module becomes more reliable with experience. Both RL and WM modules are subject to forgetting (decay parameters φ_RL and φ_WM). We constrain φ_RL < φ_WM consistent with WM's dependence on active memory).

Learning model details

RL model.

All models include a standard RL module with simple delta rule learning. For each stimulus s and action a, the expected reward Q(s, a) is learned as a function of reinforcement history. Specifically, the Q value for the selected action given the stimulus is updated upon observing each trial's reward outcome r_t (1 for correct, 0 for incorrect) as a function of the prediction error (PE) between expected and observed reward at trial t as follows:

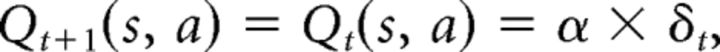where δ_t = r_t − Q_t(s, a) is the PE, and α is the learning rate. Choices are generated probabilistically with greater likelihood of selecting actions that have higher Q values using the following softmax choice rule:

where β is an inverse temperature determining the degree with which differences in Q values are translated into more deterministic choice and the sum is over the three possible actions a_i.

Undirected noise.

The softmax temperature allows for stochasticity in choice, but where stochasticity is more impactful when the value of actions are similar to each other. We also allow for “slips” of action (“irreducible noise,” i.e., even when Q value differences are large). Given a model's policy π = p(a|s), adding undirected noise consists of defining the new mixture policy as follows:

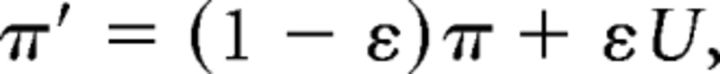where U is the uniform random policy (U(a) = 1/n_A, n_A = 3), and the parameter 0 < ε < 1 controls the amount of noise (Collins and Koechlin, 2012; Guitart-Masip et al., 2012; Collins and Frank, 2013). Nassar and Frank (2016) showed that failing to take into account this irreducible noise can render fits to be unduly influenced by rare odd datapoints (e.g., that might arise from attentional lapses) and that this problem is remedied by using a hybrid softmax-ε-greedy choice function as used here.

Forgetting.

We allow for potential decay or forgetting in Q values on each trial, additionally updating all Q values at each trial, according to the following:

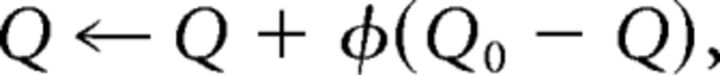where 0 < φ < 1 is a decay parameter pulling at each trial the estimates of values toward initial value Q₀ = 1/n_A. This parameter allows us to capture delay-sensitive aspects of WM, where active maintenance is increasingly likely to fail with intervening time and other stimuli, but also allows us to separately estimate any decay in RL values (which is typically substantially lower than in WM).

Perseveration.

To allow for potential neglect of negative as opposed to positive feedback, we estimate a perseveration parameter pers such that, for negative PEs (delta < 0), the learning rate α is reduced by α = (1 − pers) × α. Therefore, values of pers near 1 indicate perseveration with complete neglect of negative feedback, whereas values near 0 indicate equal learning from negative and positive feedback.

WM.

To implement an approximation of a rapid updating but capacity-limited WM, this module assumes a learning rate α = 1 (representing the immediate accessibility of items in active memory), but includes capacity limitation such that only at most K stimuli can be remembered. At any trial, the probability of WM contributing to the choice for a given stimulus is w_WM(t) =P_t(WM). This value is dynamic as a function of experience (see next paragraph). Therefore, the overall policy is as follows:

where π_WM is the WM softmax policy and π_RL is the RL policy. Note that this implementation assumes that information stored for each stimulus in WM pertains to action–outcome associations. Furthermore, this implementation is an approximation of a capacity/resource-limited notion of WM. It captures key aspects of WM such as: (1) rapid and accurate encoding of information when low amount of information is to be stored; (2) decrease in the likelihood of storing or maintaining items when more information is presented or when distractors are presented during the maintenance period; and (3) decay due to forgetting. Because it is a probabilistic model of WM, it cannot capture specifically which items are stored, but it can provide the likelihood of any item being accessible during choice given the task structure and recent history (set size, delay, etc.).

Inference.

The weighting of whether to rely more on WM versus RL is dynamically adjusted over trials within a block based on which module is more likely to predict correct outcomes. The initial probability of using WM w_WM(0) = P₀(WM) is initialized by the a priori use of WM, as defined above, w_WM(0) = ρ × min(1, K/n_s), where ρ is a free parameter representing the participant's overall reliance on WM over RL.

On each correct trial, w_WM(t) = P_t(WM) is updated based on the relative likelihood that each module would have predicted the observed outcome given the selected correct action a_c; specifically:

• for WM, p(correct|stim, WM) = W_WM π_WM(a_c) + (1 − w _WM)1/n_A

• for RL, p(correct|stim, RL) is simply π_RL (a_c)

The mixture weight is updated by computing the posterior using the previous trial's prior, and the above likelihoods, such that

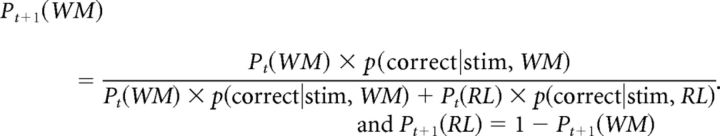Models considered.

We combined the previously described features into different learning models and conducted extensive comparisons of multiple models to determine which fit the data best (penalizing for complexity) so as to validate the use of this model in interpreting subjects' data. For all models we considered, adding undirected noise, forgetting, and perseveration features significantly improved the fit, accounting for added model complexity (see model comparisons).

This left three relevant classes of models to consider: The RL model combines the basic delta rule RL with forgetting, perseveration, and undirected noise features. It assumes a single system that is sensitive to delay and asymmetry in feedback processing. This is a five-parameter model (learning rate α, sofmax inverse temperature β, undirected noise ε, decay φ_RL, and pers parameter). The RL6 model is identical to the previous one, with the variant that learning rate can vary as a function of set size. We have shown previously that although such a model can capture the basic differences in learning curves across set sizes by fitting lower learning rates with higher set sizes, it provides no mechanism that would explain these effects and still cannot capture other more nuanced effects (e.g., changes in the sensitivity to delay with experience). However, it provides a benchmark to compare with RLWM. This is a 10-parameter model (six learning rate α_n's, sofmax inverse temperature β, undirected noise ε, decay φ_RL, and the pers parameter). RLWM is the main model, consisting of a hybrid between RL and WM. RL and WM modules have shared softmax β and pers parameters, but separate decay parameters, φ_RL and φ_WM, to capture their differential sensitivity to delay. WM capacity is 0 < K < 6, with an additional parameter for overall reliance on WM 0 < ρ < 1. Undirected noise is added to the RLWM mixture policy. This is an 8-parameter model (capacity K, WM reliance ρ, WM decay φ_WM, RL learning rate α, RL decay φ_RL, softmax inverse temperature β, undirected noise ε, and the pers parameter).

In the RLWM model presented here, the RL and WM modules are independent and only compete for choice at the policy level. Given our findings showing an interaction between the two processes, we also considered variants of RLWM including mechanisms for interactions between the two processes at the learning stage. These models provided similar fit (measured by the Akaike information criterion, AIC) to the simpler RLWM model. We chose to use the simpler RLWM model because the more complex model is less identifiable within this experimental design, providing less reliable parameter estimates and regressors for model-based analysis.

RLWM fitting procedure.

We used MATLAB optimization under the constraint function fmincon to fit parameters. This was iterated with 50 randomly chosen starting points to increase the likelihood of finding a global rather than local optimum. For models including the discrete capacity K parameter, this fitting was performed iteratively for capacities K = {1, 2, 3, 4, 5} using the value gave the best fit in combination with other parameters.

Softmax β temperature was fit with constraints [0 100]. All other parameters were fit with constraints [0 1]. We considered sigmoid-transforming the parameters to avoid constraints in optimization and obtain normal distributions, but although fit results were similar, distributions obtained were actually not normal. Therefore, all statistical tests on parameters were nonparametric. See Table 1 for fit parameter statistics.

Table 1.

RLWM model fit parameters

	K	α	φWM	ρ	φRL	ϵ	pers
Parameter statistics
Mean (SD)	4.08 (0.98)	0.07 (0.13)	0.29 (0.31)	0.86 (0.18)	0.05 (0.05)	0.03 (0.03)	0.34 (0.31)
Median	4	0.03	0.18	0.94	0.05	0.03	0.25
Min−max	2–5	0.01–0.5	0–1	0.42–1	0–0.21	0–0.14	0.02–1
Correlation between parameters
α	NS
φWM	NS	0.77
ρ	NS	−0.65	−0.77
φRL	NS	0.83	0.69	−0.62
ϵ	NS	NS	NS	NS	NS
pers	NS	NS	NS	NS	NS	NS

NS, Nonsignificant correlation (p < 0.05, corrected for multiple comparisons).

Other competing models

To further test whether “single-system” models, as opposed to hybrid models including an RL and a WM component, could account for behavior, we tested other algorithms embodying alternative assumptions in which behavior is governed by a single learning process (either RL or WM).

The WMd model is similar to a WM module, with the following changes: there is no capacity limitation and, instead of being fixed, the decay parameter is fixed to an initial value which then decreases toward 0 with each stimulus encounter, modeling the possibility that forgetting in WM itself might decrease with practice. This model includes five parameters: β, ε, and pers as defined above; the initial value of decay decay₀; and ξ, the decay factor. The WMdi model adds an interference mechanism to WMd such that the decay factor of a given stimulus additionally increases with every encounter of a different stimulus. This adds one parameter to the previous model. The RLi model is identical to the basic RL model with an added interference mechanism: on each trial, the Q value of nonobserved stimuli with the chosen action is updated in the same way as the observed stimuli, but with a fraction of the learning rate α_i. This captures the possibility that credit is assigned to the wrong stimulus, modeling the possibility that WM-like effects might reflect interference within a pure RL system. This model includes six parameters.

Model comparison.

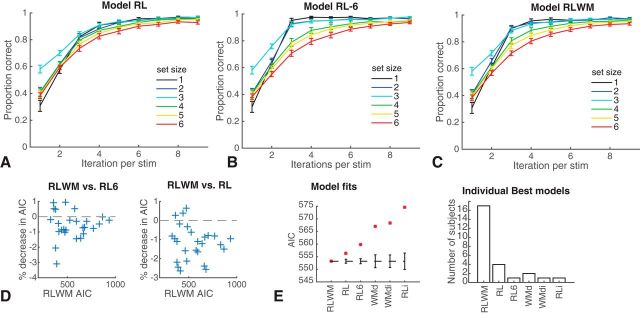
We used AIC to penalize model complexity (Burnham and Anderson, 2002). We showed previously that, in the case of the RLWM model and its variants, AIC was a better approximation than the Bayesian information criterion (Schwarz, 1978) at recovering the true model from generative simulations (Collins and Frank, 2012). Comparing RLWM, RL6, and RL-only showed that models RL6 and RL-only were strongly nonfavored, with probability 0 over the whole group. Other single-process models were also unable to capture behavior better than RLWM (see Fig. 3E).

Figure 3.

Model validation. A–C, Proportion of correct responses as a function of how many times a specific stimulus was encountered, for each set size, for simulation of different models with individually fit parameters. Models were simulated 100 times per subject and then averaged within subjects to represent this subject's contribution. Error bars indicate SEM across subjects. A, Simple RL model including decay and different sensitivity to gains/losses. B, Identical model to A but with learning rate varying per set size. C, Model incorporating both RL and WM. D, Model comparisons show a significantly lower AIC for RLWM than RL6 or RL for a significant number of subjects. Each cross indicates a single subject. E, Model comparison with other potential models show best fit for RLWM (see Materials and Methods for other model names).

Model simulation.

Model selection alone is insufficient to assess whether the best fitting model sufficiently captures the data. To test whether models capture the key features of the behavior (e.g., learning curves), we simulated each model with fit parameters for each subject, with 100 repetitions per subject, and then averaged to represent this subject's contribution. To account for initial biases, we assume that the model's choice at first encounter of a stimulus is identical to the subjects, whereas all further choices are selected randomly from the model's learned values and policies.

fMRI recording and preprocessing

Whole-brain imaging was performed on a Siemens 3T TIM Trio MRI system equipped with a 32-channel head coil. A high-resolution T1-weighted 3D multiecho MPRAGE image was collected from each participant for anatomical visualization. Functional images were acquired in one run of 1920 volume acquisitions using a gradient-echo, echoplanar pulse sequence (TR 2 s, TE 28 ms, flip angle 90, 40 interleaved axial slices, 192 mm field of view with 3 × 3 × 3 mm voxel size). Stimuli were presented on a BOLD screen display device (http://www.crsltd.com/tools-for-functional-imaging/mr-safe-displays/boldscreen-24-lcd-for-fmri/) located behind the scanner and made visible to the participant via an angled mirror attached to the head coil. Padding around the head was used to restrict head motion. Participants made their responses using an MRI-compatible button box.

Functional images were preprocessed in SPM8 (http://www.fil.ion.ucl.ac.uk/spm). Before preprocessing, data were inspected for artifacts and excessive variance in global signal (functions: tsdiffana, art_global,art_movie). Functional data were corrected for differences in slice acquisition timing by resampling slices to match the first slice. Next, functional data were realigned (corrected for motion) using B-spline interpolation and referenced to the mean functional image. Functional and structural images were normalized to Montreal Neurological Institute (MNI) stereotaxic space using affine regularization, followed by a nonlinear transformation based on a cosine basis set, and then resampled into 2 × 2 × 2 mm voxels using trilinear interpolation. Last, images were spatially smoothed with an 8 mm full-width at half-maximum isotropic Gaussian kernel.

GLMs

A temporal high-pass filter of 400 s (0.0025 Hz) was applied to our functional data to remove noise but preserve power from low-frequency regressors. Changes in MR signal were modeled using a general linear model (GLM) approach. Our GLM included six onsets regressors, one for correct trials corresponding to each set size (one through six). Each onset was coded as a boxcar of 2 s in length that encompasses stimulus presentation, response, and feedback. Each onset regressor was modulated by a PE parametric regressor. We modeled error trials, no response trials, and instructions (one instruction screen at the beginning of each block, 18 total, each 10 s in length) as separate regressors. Note that error trials across all set sizes were binned into one regressor due to the low number of error trials in low set sizes. Finally, we included nuisance regressors for the six motion parameters (x, y, z, pitch, roll, and yaw) and a linear drift over the course of the run. SPM-generated regressors were created by convolving onset boxcars and parametric functions with the canonical hemodynamic response (HRF) function and the temporal derivative of the HRF. Beta weights for each regressor were estimated in a first-level, subject-specific fixed-effects model. For group analysis, the subject-specific β estimates were analyzed with subject treated as a random effect. At each voxel, a one-sample t test against a contrast value of zero gave us our estimate of statistical reliability. For whole-brain analysis, we corrected for multiple comparisons using cluster correction, with a cluster-forming threshold of p < 0.001 and an extent threshold calculated with SPM to set a familywise error cluster level corrected threshold of p < 0.05 (127 for PE > fixation; 267 for the PE * set size interaction). Note that these appropriately high-cluster-forming threshold ensures that parametric assumptions are valid and the rate of false positives are appropriate (Eklund et al., 2016; Flandin and Friston, 2016).

ROIs

Because we did not have specific regional predictions regarding the WM component of learning, we defined broad frontoparietal networks as ROIs that have been associated previously with a wide range of tasks involving cognitive control. Specifically, our first control network ROIs were defined by using left and right anterior dorsal premotor cortex (prePMd: 8 mm sphere around −38 10 34; Badre and D'Esposito, 2007) as seeds in two separate “resting-state” (task-free) seed-to-voxel correlation analyses in the CONN toolbox (https://www.nitrc.org/projects/conn/) and using the corresponding whole-brain connectivity to left and right prePMd as our control network ROI. To confirm the robustness of our findings, we then ran a larger frontoparietal network ROI defined from a functionally neutral group (Yeo et al., 2011), along with a functionally defined ROI of the multiple demands network from Fedorenko et al. (2013). All three of these frontoparietal ROIs yielded similar outcomes, thus confirming the robustness of our findings. We report here the results from Yeo et al. (2011) as the widest, most neutral ROI.

The striatum ROI was defined based on univariate activity for PE (p < 0.001, uncorrected), masked by Automated Anatomical Labeling (AAL) definitions for putamen, caudate, and nucleus accumbens (MarsBar AAL structural ROIs: http://marsbar.sourceforge.net/download.html). We note that this ROI definition would be biased for assessing the effect of RPE in the striatum. However, this was not our goal because the relationship of RPE and striatum is established both in general from the prior literature and in this study based on the corrected whole-brain analysis (see Results). Rather, this ROI will be used to test the effects of set size and the interaction of set size with RPE within regions maximally sensitive to RPE. Because the set size variable is uncorrelated with that of RPE, this ROI definition does not bias either of these analyses.

For each ROI, a mean time course was extracted using the MarsBar toolbox (http://marsbar.sourceforge.net/). The GLM design was estimated against this mean time series, yielding parameter estimates (β weights) for the entire ROI for each regressor in the design matrix.

Whole-brain contrasts.

We focus on two main contrasts, the positive effect of RPE and the positive interaction of RPE and set size, to determine whether WM processes influence RPE signaling and whether such interactions relate to behavior. The first contrast is defined by considering the sum of the β weights across all set sizes, Σ_i=1:6 β_PE(i); testing whether this contrast value is significantly positive. The second contrast takes the linear contrast of the β weights across set sizes by the set size, Σ_i=1:6 (i-3.5) * β_PE(i); testing whether this contrast is positive signals a linear increase of RPE with set size. We also tested the opposite contrasts, as well as the linear effect of set size Σ_i=1:6 (i-3.5) * β_i.

Interaction between set size and RPE.

To investigate individual differences in the interaction between set size and RPE, we assessed ROI markers of this interaction. We computed this in one of three ways, each reflecting different assumptions: (1) a linear contrast of set size on RPE regression weight; (2) a contrast of high set size (4–6) versus low set size (1–3) on RPE regression weights (in case of a step function, e.g., for above vs below capacity sets), and (3) Spearman rho of RPE weights across set sizes, which does not require linearity and is less susceptible to outliers than linear regression. Despite slightly different assumptions, all three measures are highly correlated (all rhos > 0.8, p < 10⁻⁴) and yielded qualitatively similar results. Because we observed that the results neither show linear changes across set sizes nor a step function, we report results using the measure defined as option 3.

Results

Behavior

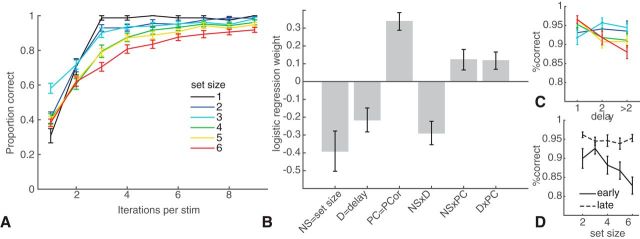
Behavioral results replicate our previous findings (Collins and Frank, 2012; Collins et al., 2014; Fig. 2). Learning curves showed strong differences as a function of set size despite the same number of encounters for each stimulus. Logistic regression analysis of subject choices (Fig. 2B) showed main effects of reward history, delay, and load, indicating that subjects were more likely to select the correct action with more previous correct experience for a given stimulus (t₍₂₅₎ = 6.8, p < 10⁻⁴) and less likely to be correct with increasing set size (t₍₂₅₎ = −3.4, p = 0.002) and increasing delay (intervening trials since their last correct choice on this stimulus; t₍₂₅₎ = −3.2, p = 0.004). There were also interactions between all pairs of factors, such that the delay effect was stronger in high load (t₍₂₅₎ = −4.4, p = 0.0002; Fig. 2C) and the effects of load and delay both decreased with more correct reward history (t > 2.1, p < 0.05; see Fig. 2D). The latter interaction is expected given the RLWM model's prediction that behavior transitions from WM (which is more sensitive to delay and load) to RL as a function of learned reliability.

Figure 2.

Behavioral results. A, Proportion of correct choices as a function of how many times a specific stimulus was encountered (i.e., learning curves) for each set size. B, Logistic regression on factors that contribute to accuracy for a given image, including set size (NS), delay since last previous correct choice for a given image (D), PCor (number of previous correct choices for that image), and their interactions. C, Illustration of the interaction between delay and set size. D, Illustration of the interaction between set size and PCor-early indicates PCor < 4; late indicates PCor > 6. Error bars indicate SEM.

Model fitting

Model fitting also confirmed our previous findings, showing that a computational model including two modules (RL and WM) explained subjects' behavior better than variants of a model assuming a single RL or WM process. Specifically, RLWM provided a significantly better AIC than RL6 (t₍₂₅₎ = 3.9, p = 0.001) and RL (t₍₂₅₎ = −6.6, p < 10⁻⁴) and individual AICs favored RLWM for a significant number of subjects (21/26 for RL6, sign test p = 0.002; 23/26 for RL, p < 10⁻⁴). Model simulations show that a simple RL model cannot capture the behavior as well as RLWM or RL6, but note that RL6 needs too many parameters to appropriately capture behavior. Pure WM models assuming changes in decay with experience, or interference, also cannot capture behavior as well as our hybrid RLWM model (Fig. 3E).

Imaging results

Whole-brain analysis showed increasing activity with set size in bilateral precuneus and decreasing activity in a network including bilateral superior frontal gyrus, bilateral angular gyrus, and bilateral supramarginal gyrus (Table 2), confirming that the set size manipulation is effective at differentially engaging large brain networks.

Table 2.

Main effect of set size

Region	BA	Extent (voxels)	x	y	z	Peak t value
Contrast: set size parametric increasing
Left precuneus	7	1948	−6	−72	44	6.98
Left angular gyrus	40		−32	−50	36	6.4
Right precuneus	7		12	−70	44	5.22
Contrast: set size parametric decreasing
Right superior frontal gyrus	9	1344	14	58	34	6.64
Left superior frontal gyrus	9		−12	46	42	4.69
	10		−4	58	28	4.5
Left supramarginal gyrus	40	447	−64	−44	34	6.31
Left angular gyrus	39		−52	−70	28	5.83
	40		−60	−52	40	4.52
Right angular gyrus	40	255	58	−52	44	5.41
	22		62	−54	28	4.41
Right supramarginal gyrus	40		64	−46	36	5.19
Right superior frontal gyrus	8	239	14	20	62	5.15
	9		10	38	52	4.42
Left superior frontal sulcus	8	255	−24	22	58	4.9
Left middle frontal gyrus	46		−24	18	40	4

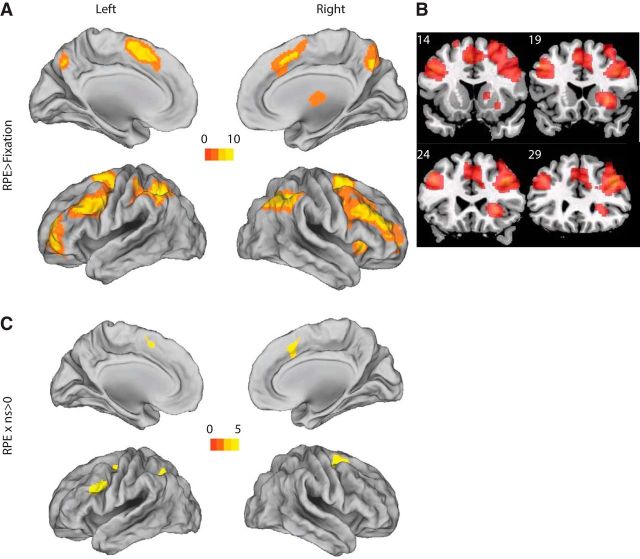
Whole-brain analysis showed a distributed network that positively correlated with the parametric RPE regressor. We verified RPE-related activation in the right caudate nucleus and thalamus (Table 3; for full results, see Fig. 4B), as expected from the literature. Notably, the RPE network also includes regions of bilateral prefrontal and parietal cortex commonly observed in cognitive control tasks.

Table 3.

Main effect of RPE

Region	BA	Extent (voxels)	x	y	z	Peak t value
Contrast: main effect of RPE > fixation
Right angular gyrus	7	3202	34	−60	42	10.83
	40		46	−52	44	9.2
Right inferior parietal gyrus	40		42	−42	40	10.21
Left superior parietal gyrus	7	3317	−30	−54	44	10.43
Left angular gyrus	40		−46	−48	56	10.32
Left inferior parietal gyrus	40		−42	−42	42	9.45
Right superior frontal sulcus	6	12409	20	2	62	9.64
Right middle frontal gyrus	46		38	36	30	8.84
Left superior frontal gyrus	6		−24	−6	62	8.15
Left middle frontal gyrus	11	1686	−30	56	4	7.78
Left lateral orbital gyrus	46		−40	56	−2	6.96
Left anterior orbital gyrus	11		−24	44	−14	6.42
Right putamen		955	28	22	0	6.99
Right thalamus			12	−10	10	5.15
Right pallidum			12	0	6	4.36
Right precuneus	7	731	6	−64	40	6.32
	7		8	−66	58	5.21
Contrast: main effect of RPE < fixation
Right superior occipital gyrus	18	9715	16	−92	24	10.22
Left superior occipital gyrus	18		−16	−96	18	8.73
Right inferior lingual gyrus	30		−10	−48	−6	8.9
Left cingulate gyrus (subgenual)	11	2264	−4	28	−12	8.52
	25		−2	18	−8	7.34
Left superior frontal gyrus	10		−8	58	2	7.24
Left middle temporal gyrus	20	2543	−56	−8	−18	6.69
Left supramarginal gyrus	48		−36	−36	22	6.26
Left superior temporal gyrus	38		−34	8	−20	6.24
Right precentral sulcus	4	1248	26	−30	66	6.21
Right postcentral gyrus	4		36	−26	72	6.13
Right precentral gyrus	4		52	−12	58	5.62
Right superior temporal gyrus	38	336	30	10	−28	6.08
Right middle temporal gyrus	21		50	2	−26	5.56
	21		58	0	−24	4.76
Right cingulate gyrus	23	516	6	−20	44	5.64
Right superior frontal gyrus	6		12	−18	62	5.03
Right cingulate sulcus	4		10	−16	54	4.56
Right superior temporal gyrus	48	935	54	−4	4	5.6
Right lateral fissure	48		50	4	−6	5.11
Right lateral fissure/insular gyrus	48		40	−14	20	5.04

All clusters reliable at p < 0.05, corrected. Coordinates are the center of mass in MNI.

Figure 4.

Whole-brain effects of RPE and RPExns. A, B, Regions positively correlated with RPE (p < 0.05, cluster corrected). C, Regions showing a positive interaction of RPE with set size.

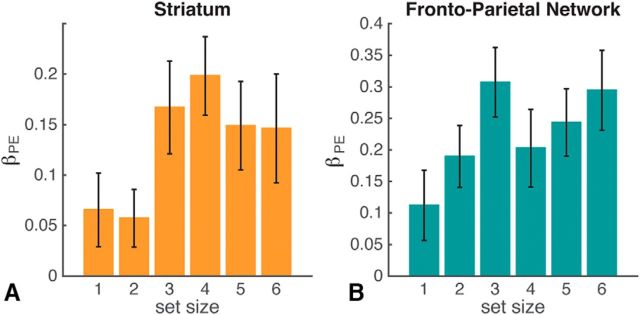
We next tested whether the RPE signal was homogeneous across set sizes in striatum, as implicitly expected if striatal RL is independent of WM. To the contrary, we found a significant positive interaction of set size with RPE (t₍₂₀₎ = 2.4, p = 0.026; Fig. 5B) in the striatal ROI (see Materials and Methods). Note that this interaction reflects a stronger effect of RPE on the striatal BOLD signal at higher set sizes (i.e., under more cognitive load). This finding supports the hypothesis that WM interacts with RL, showing blunted RL signals in low set sizes (i.e., within the capacity of WM).

Figure 5.

Striatum and frontoparietal ROIs show increased RPE effects in higher set sizes. Average β coefficient for RPE regressor per set size for striatal ROI (A) and frontoparietal network ROI (B) defined by Yeo et al. (2011). Error bars indicate SEM.

Next, we investigated whether other brain regions showed the same modulation of RPE signaling by WM load. Whole-brain analysis showed a positive linear interaction of set size with RPE in left lateral prefrontal cortex and parietal cortex (MNI coordinates −38, 20, 28; Table 4). Further investigation within an independent frontoparietal network ROI (Yeo et al., 2011) showed both a strong main effect of PE (t₍₂₀₎ = 6.9, p < 10⁻⁴) and a significant interaction of set size with RPE in the frontoparietal ROI (t₍₂₀₎ = 2.3, p = 0.03), a pattern similar to the striatum ROI. Again, RPE signaling was larger with more WM load, possibly reflective of a common neuromodulatory signal in striatum and cortex influenced by cognitive demands.

Table 4.

Set size * RPE interaction^a

Region	BA	Extent (voxels)	x	y	z	Peak t value
Left superior precentral sulcus	44	725	−46	10	36	5.69
Left inferior frontal sulcus	48		−38	20	28	5.16
Left middle frontal gyrus	6		−32	2	38	4.57
Right superior frontal gyrus	6	689	18	4	54	5.42
	32		6	22	46	4.3
Left superior frontal gyrus	6		−6	10	50	4.08
Left intraparietal sulcus	7	463	−26	−66	44	5.28
	7		−30	−58	46	5.24
	19		−26	−68	34	4.59

Contrast: RPE parametric increasing with set size.

Link to behavior

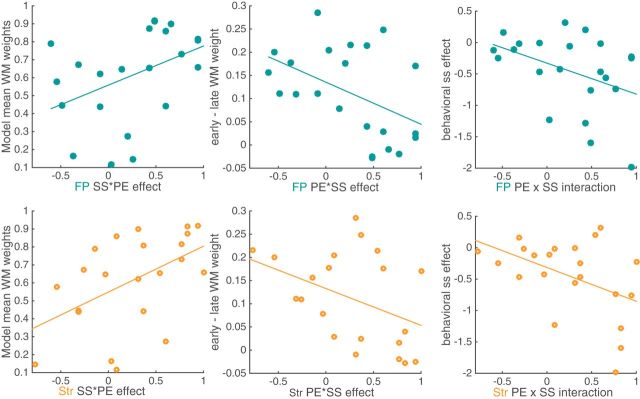
We hypothesized that the weaker RPE signals observed in low set sizes might reflect an interaction between WM and RL systems. Specifically, this may reflect the greater use of WM, instead of RL, at low set sizes. This strategy could be because low set sizes do not require RPE signaling: the most recent stimulus–action–outcome can be accessed from memory. Therefore, we predicted that those subjects relying more on WM would exhibit a stronger neural interaction effect (i.e., they would show less homogeneity in their RPE signals across set sizes). To index WM contributions to choice, we use the computational model-inferred weight of the WM module averaged over all trials. Indeed, we found that greater WM contributions to choices was significantly related to the set size effect on RPE signaling, both in striatum (ρ = 0.55, p = 0.01), and the frontoparietal ROI (ρ = 0.49; p = 0.02) (Fig. 6, left). Moreover, subjects who continued to rely on WM with experience (i.e., exhibiting less transition to RL) also showed greater set size effects on RPE signaling in FP (ρ = −0.46, p = 0.03) and, marginally, in striatum (ρ = −0.41; p = 0.06) (Fig. 6, middle). This may be due to the fact that, for participants with higher overall reliance on WM, the WM module is more reliable, so WM use decreases less over learning. Indeed, the two indexes were negatively correlated (ρ =-0.69, p < 10⁻³). The results were partly accounted for by differences in model fit capacity parameter: subjects with higher capacity showed significantly stronger nsxRPE interaction in FP (ρ = 0.46, p = 0.03) and marginally so in striatum (ρ =.41, p = 0.06). Finally, we confirmed this effect was independent of the fit of the RLWM model using logistic regression, specifically, the effect of set size on accuracy (note that this measure was, as expected, related to the one obtained by the computational model: Spearman ρ = −0.42, p = 0.05). Indeed, the effect of set size on accuracy was marginally related to the set size by RPE interaction in striatum (ρ = −0.4, p = 0.06; Fig. 6, right) and FP (ρ = −0.41, p = 0.06). Again, neural interactions were stronger for those subjects exhibiting a stronger negative effect of set size on behavior.

Figure 6.

Effect of set size on RPE in the fMRI signal is related to individual differences in behavior. Left, Average model-inferred mixture weight assigned to WM over RL (“Model mean WM weight”) is significantly related to a stronger effect of set size in frontoparietal ROI (ρ = 0.49, p = 0.02) and in the striatum (ρ = 0.55, p = 0.01). Middle, Decrease in WM weight from early (first 3 iterations) to late in a learning block (last 3 iterations) is significantly related to fMRI effect in FP ROI (ρ= −0.46, p = 0.03) and marginally so in striatum (ρ= −0.41, p = 0.06). Right, Behavioral set size effect is measured as the logistic regression weight of the set size predictor; stronger behavioral effect is marginally related to a stronger neural effect in FP ROI (ρ= −0.41, p = 0.059) and in striatum ROI (ρ = 0.4, p = 0.063).

Discussion

We combined computational modeling and fMRI to investigate the contributions of two distinct processes to human learning: RL and WM. We replicated our previous results (Collins and Frank, 2012; Collins et al., 2014) showing that these jointly play a role in decisions: computational models assuming a single learning process (either WM or RL) could not capture behavior adequately. We also replicated the widespread observation that the striatum and lateral prefrontal cortex are sensitive to RPEs, a marker of RL. We made the novel observation that RL and WM are not independent processes, with the most commonly studied RL signal blunted under low WM load. Further, we found that the degree of interaction was related to individual differences in subjects' use of WM: the more robustly subjects used WM for learning, the more they showed WM effects on RL signals.

The process of model-free RL, as both a class of machine learning algorithms and as the neural network function implemented via dopamine-dependent plasticity in corticobasal ganglia networks, is characterized by integration of rewards over time to estimate the value of different options and a value-dependent policy. Our behavioral results replicate our previous work showing that, even in simple instrumental learning, we cannot account for human learning based only on the integrated history of reward. Instead, the influences of load and delay/intervening trials show that WM also contributes to learning. That this influence decreases with experience supports a model in which RL and WM modules are dynamically weighted according to their success in predicting observed outcomes.

We used computational modeling to disentangle the contributions of RL and WM to learning and to assess neural indicators of their interactions. We extracted the RPE signal from the RL module and confirmed in a model-based whole-brain fMRI analysis that striatum was sensitive to PEs, as established in many studies (Pessiglione et al., 2006; Schönberg et al., 2007), as was a large bilateral frontoparietal region (Daw et al., 2011). However, we found in both regions that sensitivity to RPE was modulated by set size, the number of items that subjects learned about in a given block. Specifically, the RPE signal was weaker in lower set sizes, in which subjects' learning was closest to optimal, and thus likely to mostly use WM. Therefore, as noted in our earlier studies (Collins and Frank, 2012; Collins et al., 2014), WM contributions to learning can confound measures typically attributed to RL. Although the previous findings were limited to behavioral, genetic, and computational model parameters, here, we report for the first time that even neural RPE signals are influenced by WM. These results also imply that in other studies that do not manipulate WM load during learning, the contribution of WM to learning may yield inflated or blunted estimates of the pure RL process.

We further found that individual differences in the degree to which set size modulated RPE signals correlated with the degree to which subjects relied on WM in their behavioral learning curves. Specifically, subjects with more robust use of WM showed more reliably blunted RPE signals in lower set sizes, supporting the interpretation that WM use induces weaker RPEs in the RL system. Further supporting this interpretation, we observed that subjects who continued to use WM with learning (i.e., showing less transition to RL) exhibited larger effects of set size on RPE signaling.

One might expect to observe more reliable indicators of neural computations with easier tasks, but our findings show the opposite. These results thus strongly hint at a mechanism by which WM and RL interact beyond the competition for control of action (Poldrack et al., 2001) and specifically at a mechanism by which WM interferes with RL computations. How might this interference occur? One possibility is that the two processes compete, not only for guiding action, but also more generally, for example, based on their reliability in a given environment. Such interference would mean that, in conditions in which WM performs better that RL (e.g., early in learning for low set sizes), WM inhibits the whole RL mechanism and thus weakens its characteristic neural signals such as RPEs. Another possible explanation for the observed interference is cooperative interaction, in which WM modifies the reward expectations in the RL system. This would lead, when WM was working well, to higher expectations than would be computed by pure RL and thus to weaker RPEs. Future research will need to distinguish these possibilities. There may be other interpretations of the change in RPE signaling with set size, in addition to our interpretation as an interaction between the RL and WM processes. However, given that behavioral fits strongly implicate separate WM and RL processes in learning (see above and previous studies) and that WM is sensitive to load in other paradigms with similar profiles, this remains the most parsimonious explanation. Note that this interaction also makes other behavioral predictions suggesting that reinforcement value learning is actually enhanced under high WM load; we have recently confirmed this prediction using a novel task building on this line of work (A.G.E. Collins, M.A. Albrecht, J.A. Waltz, J.M. Gold, and M.J., unpublished data).

Our results are related to recent work on sequential decision making and learning that highlighted the role of a model-free module (similar to our RL model) and of a model-based module responsible for representing stimulus–action–outcome transitions and using them to plan decisions (Doll et al., 2015). This latter module has been linked to cognitive control and is weakened under load (Otto et al., 2013), suggesting that it may require WM. Moreover, both WM use in the current task and model-based processing in the sequential task are related to the same genetic variant associated with prefrontal catecholaminergic function (Collins and Frank, 2012; Doll et al., 2016). Notably, Daw et al. (2011) showed that RPEs in the striatum were modulated by model-based values, a result that may support our collaborative hypothesis. However, we demonstrate such interaction even in paradigms that are traditionally thought to involve purely “model-free” RL. Because there is no sequential dependence between trials, learning in our paradigm does not require learning a transition model or planning. Indeed, we could adequately capture learning curves for individual set sizes using a purely model-free RL model (Collins and Frank, 2012; Collins et al., 2014), with decreasing learning rates across set sizes, but this model has more parameters than RLWM and cannot capture the nuanced effects of, for example, delay and set size interactions. Therefore, our results show that learning in very simple environments that appear to require purely model-free learning still recruits executive functions, with WM contributing to learning and interfering with the putative dopaminergic RL process. Our results show a similar pattern of RPE activations for subcortical and lateral prefrontal cortex areas, a common finding in published studies (Frank and Badre, 2012; e.g., Badre and Frank, 2011), possibly reflecting a common dopaminergic input to both regions (Björklund and Dunnett, 2007).

We investigated the role of WM using set size as a proxy. However, this leaves open some questions and may limit some of our interpretations. In particular, set size affects the overall load of WM, but is also predictive of higher delays between repetitions of the same stimulus. Although our analyses tease apart load from delay, the delay itself comprises both a temporal component (number of seconds over which WM could decay passively) and a discrete component (number of intervening trials that may interfere with WM). Our paradigm did not manipulate those two factors to make them maximally decorrelated and cannot distinguish their relative contributions to the effect of delay on behavior. Furthermore, by focusing on set size as the marker of WM, we cannot distinguish between a “tonic,” or slowly tuned interference of WM in RL computation, and a more “phasic,” trial-by-trial adjustment of their role and interaction between them. A target for future research is increasing the experimental paradigm's capacity to disentangle delay from load carefully, allowing us to better understand the dynamics of interactions between RL and WM.

We focused on WM as an alternative learning mechanism from RL, with an a priori interest in regions of the cognitive control network in lateral frontal and parietal cortices. However, regions involved in long-term memory (LTM), such as the medial temporal lobe (MTL) and hippocampus, could also play an important role: rote memorization of explicit rules is in the prime domain of LTM. Others have shown trade-offs for learning between LTM and striatal-based learning (Poldrack et al., 2001) and WM itself is often difficult to distinguish from LTM (Ranganath and Blumenfeld, 2005; D'Esposito and Postle, 2015). Our results are consistent with LTM having a role in learning: indeed, we observed a negative correlation between RPE and activation in a network of regions including MTL (Table 4), indicating higher activation early in learning (Poldrack et al., 2001). However, computational modeling shows that the second learning component that we extracted is capacity limited, supporting our interpretation of this component as mainly WM. Nevertheless, future research is needed to dissociate more carefully the role of WM from LTM in RL.

Learning is a key factor in humans for improving our abilities, skills, and fitting to our quickly changing environments. Understanding what distinct cognitive and neurological components contribute to learning is thus essential, in particular studying differences in learning across individuals. Many neurological and psychiatric disorders include learning impairments (Huys et al., 2016). To understand precisely how learning is affected by these conditions, we must be able to extract separable cognitive factors reliably, understand how these factors interact, and link them to their underlying neural mechanisms. Our results provide a first step toward clarifying how we trade off WM and integrative value learning to make decisions in simple learning environments and how these processes may interfere with each other.

Notes

Supplemental material for this article is available at https://www.ocf.berkeley.edu/∼acollins/pdfs/papers/RLWMfMRI_SIDocument.pdf. This material has not been peer reviewed.