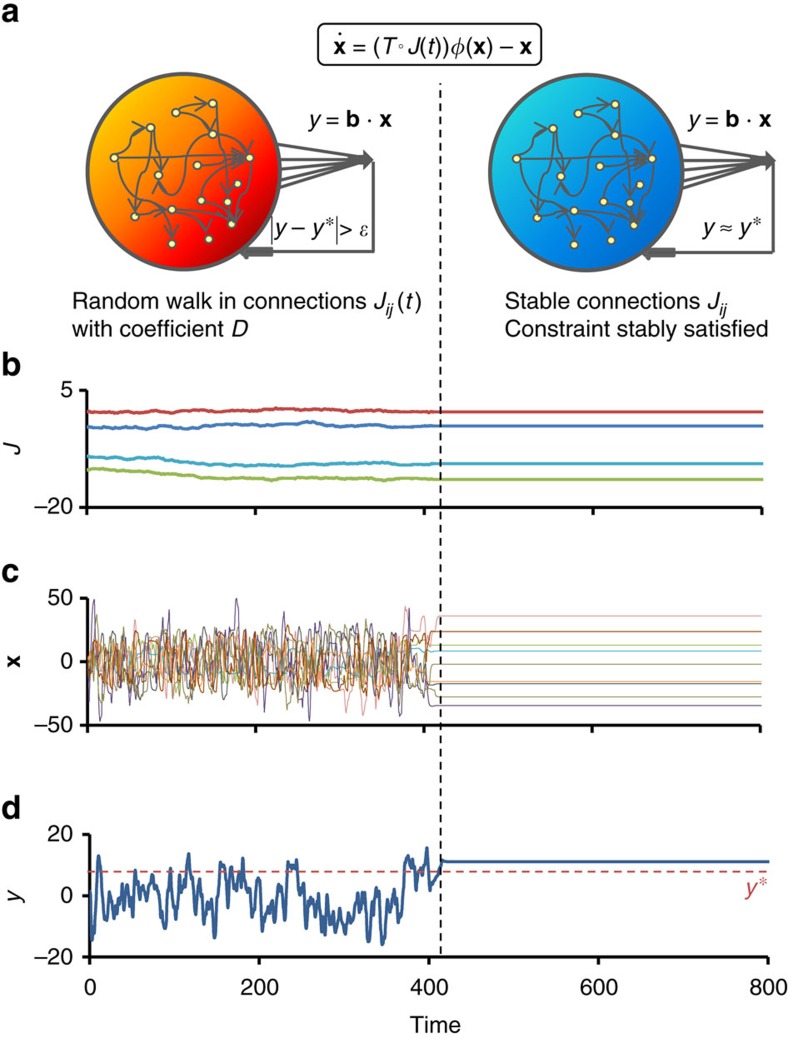
Figure 1. Exploratory dynamics and convergence to a constraint-satisfying stable state.

(a) Schematic representation of the model: a random N × N network, composed of an adjacency matrix T and an interaction strength matrix J, governs a nonlinear dynamical system (equation in box; φ(x)=tanh(x)). The resulting spontaneous dynamics are typically irregular for large enough interactions. A macroscopic variable, the phenotype y, is subject to an arbitrary constraint y≈y* with finite precision ɛ. When the constraint is not met (left; ‘hot' regime), the connections strengths J_ij undergo a random walk with magnitude determined by the coefficient D and the mismatch function 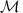(y−y*). The random walk stops when the mismatch is stably reduced to zero (right; ‘frozen' regime). (b–d) Example of exploration and convergence. Shown are representative trajectories of connection strengths (b), microscopic variables (c) and the phenotype y (d) before and after convergence to a stable state satisfying the constraint. The network in this example has scale-free (SF) out-degree distribution (a=1, γ=2.4) and Binomial in-degree distribution 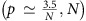. N=1,000, y*=10, D=10⁻³, g₀=10. See Methods for more details.