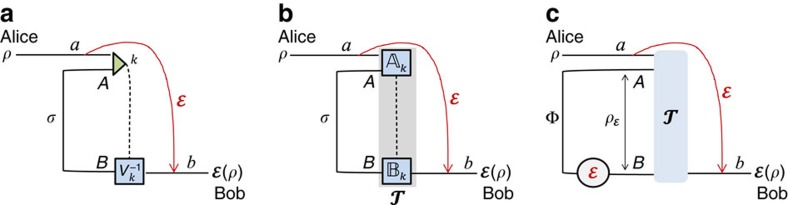
Figure 2. From teleportation- to LOCC-simulation of quantum channels.

(a) Consider the generalized teleportation of an input state ρ of a d-dimensional system a by using a resource state σ of two systems, A and B, with corresponding dimensions d and d′ (finite or infinite). Systems a and A are subject to a Bell detection (triangle) with random outcome k. This outcome is associated with a projection onto a maximally entangled state up to an associated teleportation unitary U_k which is a Pauli operator for d<+∞ and a phase-displacement for d=+∞ (see Methods for the basics of quantum teleportation and the characterization of the teleportation unitaries). The classical outcome k is communicated to Bob, who applies a correction unitary 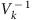to his system B with output b. In general, V_k does not necessarily belong to the set {U_k}. On average, this teleportation LOCC defines a teleportation channel 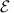from a to b. It is clear that this construction also teleports part a of an input state involving ancillary systems. (b) In general we may replace the teleportation LOCC (Bell detection and unitary corrections) with an arbitrary LOCC 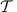: Alice performs a quantum operation 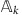on her systems a and A, communicates the classical variable k to Bob, who then applies another quantum operation 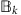on his system B. By averaging over the variable k, so that 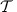is certainly trace-preserving, we achieve the simulation 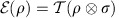for any input state ρ. We say that a channel 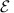is ‘σ-stretchable' if it can be simulated by a resource state σ for some LOCC 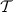. Note that Alice's and Bob's LOs 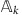and 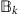are arbitrary quantum operations; they may involve other local ancillas and also have extra labels (due to additional local measurements), in which case 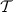is assumed to be averaged over all these labels. (c) The most important case is when channel 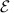can be simulated by a trace-preserving LOCC 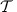applied to its Choi matrix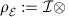 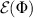, with Φ being an EPR state. In this case, we say that the channel is ‘Choi-stretchable'. These definitions are suitably extended to bosonic channels.