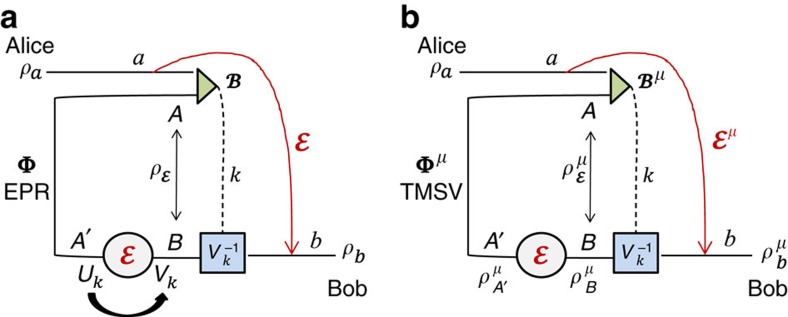
Figure 3. Teleportation-covariant channels are Choi-stretchable.

(a) Consider the teleportation of an input state ρ_a by using an EPR state Φ_AA′ of systems A and A′. The Bell detection 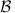on systems a and A teleports the input state onto A′, up to a random teleportation unitary, that is, ρ_A′=U_kρ_a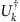. Because 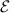is teleportation-covariant, U_k is mapped into an output unitary V_k and we may write 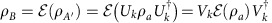. Therefore, Bob just needs to receive the outcome k and apply 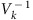, so that 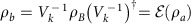. Globally, the process describes the simulation of channel 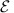by means of a generalized teleportation protocol over the Choi matrix 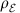. (b) The procedure is also valid for CV systems. 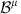If the input a is a bosonic mode, we need to consider finite-energy versions for the EPR state Φ and the Bell detection , that is, we use a TMSV state Φ^μ and a corresponding quasi-projection onto displaced TMSV states. At finite energy μ, the teleportation process from a to A′ is imperfect with some output 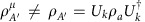. However, for any ɛ>0 and input state ρ_a, there is a sufficiently large value of μ such that 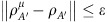(refs ²⁵, ²⁶). Consider the transmitted state 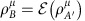. Because the trace distance decreases under channels, we have 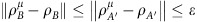. After the application of the correction unitary 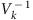, we have the output state 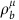which satisfies 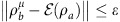. Taking the asymptotic limit of large μ, we achieve 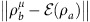→0 for any input ρ_a, therefore achieving the perfect asymptotic simulation of the channel. The asymptotic teleportation-LOCC is therefo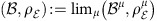re where 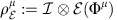. The result is trivially extended to the presence of ancillas.