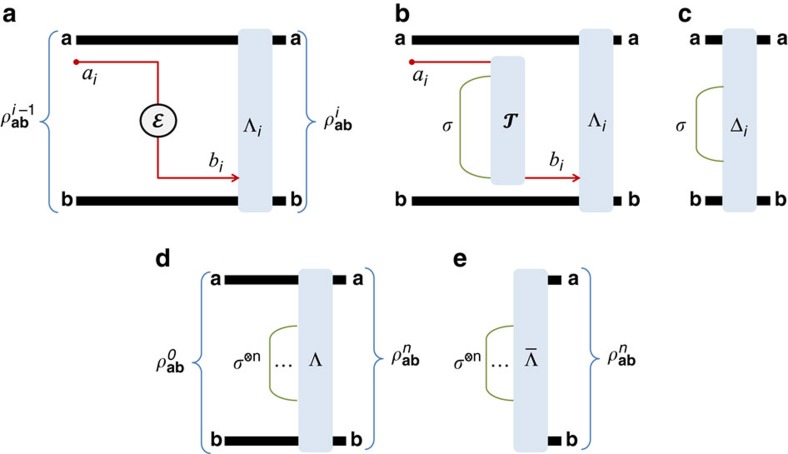
Figure 4. Teleportation stretching of an adaptive quantum protocol.
(a) Consider the ith transmission through channel 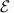 , where the input (i−1)th register state is given by
, where the input (i−1)th register state is given by 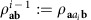 . After transmission through
. After transmission through  and the adaptive LOCC Λi, the register state is updated to
and the adaptive LOCC Λi, the register state is updated to 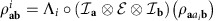 . (b) Let us simulate the channel
. (b) Let us simulate the channel 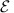 by a LOCC
by a LOCC 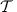 and a resource state σ. (c) The simulation LOCC
and a resource state σ. (c) The simulation LOCC 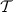 can be combined with the adaptive LOCC Λi into a single ‘extended' LOCC Δi while the resource state σ can be stretched back in time and out of the adaptive operations. We may therefore write
can be combined with the adaptive LOCC Λi into a single ‘extended' LOCC Δi while the resource state σ can be stretched back in time and out of the adaptive operations. We may therefore write 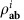 =Δi(
=Δi(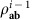 ⊗σ). (d) We iterate the previous steps for all transmissions, so as to stretch n copies σ⊗n and collapse all the extended LOCCs Δn o …o Δ1 into a single LOCC Λ. In other words, we may write
⊗σ). (d) We iterate the previous steps for all transmissions, so as to stretch n copies σ⊗n and collapse all the extended LOCCs Δn o …o Δ1 into a single LOCC Λ. In other words, we may write 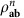 =Λ(
=Λ(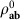 ⊗σ⊗n). (e) Finally, we include the preparation of the separable state
⊗σ⊗n). (e) Finally, we include the preparation of the separable state 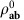 into Λ and we also average over all local measurements present in Λ, so that we may write the output state as
into Λ and we also average over all local measurements present in Λ, so that we may write the output state as 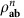 =
= (σ⊗n) for a trace-preserving LOCC
(σ⊗n) for a trace-preserving LOCC 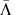 . The procedure is asymptotic in the presence of asymptotic channel simulations (bosonic channels).
. The procedure is asymptotic in the presence of asymptotic channel simulations (bosonic channels).