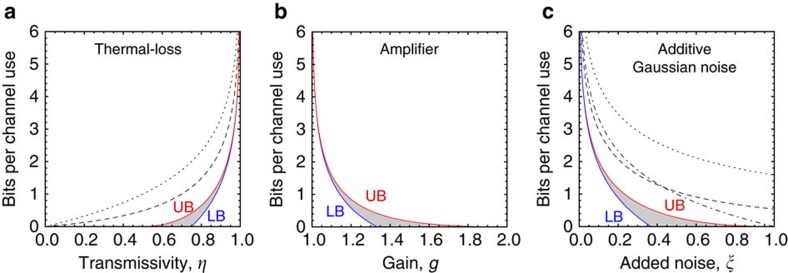
Figure 7. Two-way capacities for Gaussian channels in terms of the relevant channel parameters.
(a) Two-way capacity 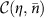 of the thermal-loss channel as a function of transmissivity η for
of the thermal-loss channel as a function of transmissivity η for 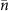 =1 thermal photon. It is contained in the shadowed area identified by the lower bound (LB) and upper bound (UB) of equation (25). Our upper bound is clearly tighter than those based on the squashed entanglement, computed in ref. 18 (dotted) and ref. 54 (dashed). Note that
=1 thermal photon. It is contained in the shadowed area identified by the lower bound (LB) and upper bound (UB) of equation (25). Our upper bound is clearly tighter than those based on the squashed entanglement, computed in ref. 18 (dotted) and ref. 54 (dashed). Note that 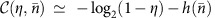 at high transmissivities. For
at high transmissivities. For 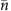 =0 (lossy channel) the shadowed region shrinks into a single line. (b) Two-way capacity
=0 (lossy channel) the shadowed region shrinks into a single line. (b) Two-way capacity 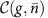 of the amplifier channel as a function of the gain g for
of the amplifier channel as a function of the gain g for 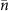 =1 thermal photon. It is contained in the shadowed specified by the bounds in equation (27). For small gains, we have
=1 thermal photon. It is contained in the shadowed specified by the bounds in equation (27). For small gains, we have 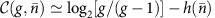 . For
. For 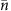 =0 (quantum-limited amplifier) the shadowed region shrinks into a single line. (c) Two-way capacity
=0 (quantum-limited amplifier) the shadowed region shrinks into a single line. (c) Two-way capacity 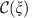 of the additive-noise Gaussian channel with added noise ξ. It is contained in the shadowed region specified by the bounds in equation (30). For small noise, we have
of the additive-noise Gaussian channel with added noise ξ. It is contained in the shadowed region specified by the bounds in equation (30). For small noise, we have 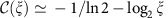 . Our upper bound is much tighter than those of ref. 18 (dotted), ref. 54 (dashed) and ref. 51 (dot-dashed).
. Our upper bound is much tighter than those of ref. 18 (dotted), ref. 54 (dashed) and ref. 51 (dot-dashed).