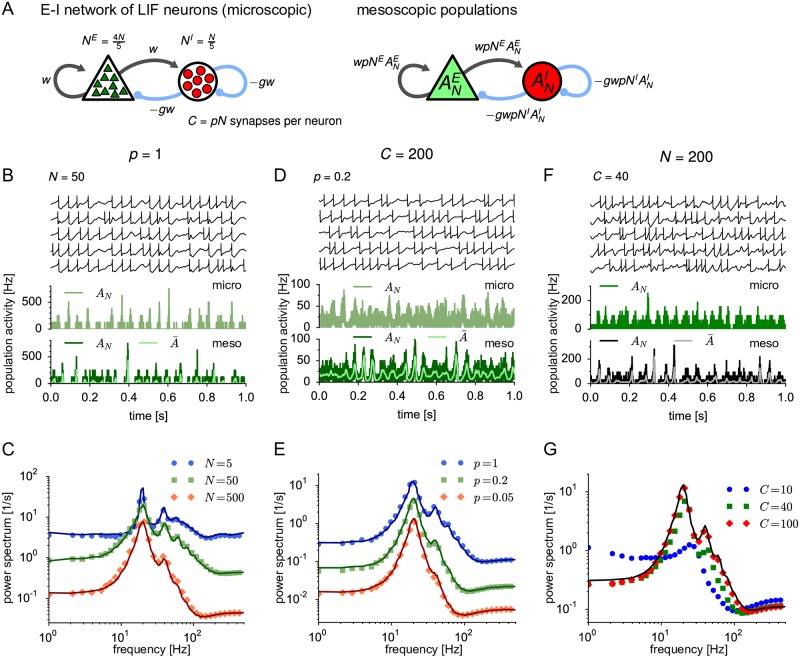
Fig 5. Mesoscopic dynamics of E-I network for varying network size N, connection probability p and number of synapses per neuron C.

(A) Left: Schematic of the network of N^E excitatory and N^I = N^E/4 inhibitory leaky integrate-and-fire (LIF) neurons, each receiving C^E = pN^E (C^I = pN^I) connections from a random subset of excitatory (inhibitory) neurons. Total numbers are N = N^E + N^I and C = C^E + C^I. At C = 200, the synaptic strength is w = 0.3 mV and −gw = −1.5 mV for excitatory and inhibitory connections, respectively. To preserve a constant mean synaptic input, the synaptic strength is scaled such that Cw = const‥ Right: Schematic of a corresponding mesoscopic model of two interacting populations. (B) Trajectories of u(t) for five example neurons (top) and of the excitatory population activity $A_N^E\left(t\right)$ obtained from the network simulation (middle) and the mesoscopic simulation (bottom, dark green) for C = N = 50; time resolution Δt = 0.2 ms. The light green trajectory (bottom panel) depicts the expected population activity ${\overline{A}}^E\left(t\right)$ given the past activity. (C) Power spectra of $A_N^E\left(t\right)$ for different network sizes while keeping p = 1 fixed (microscopic: symbols, mesoscopic: solid lines with corresponding dark colors). (D) Sample trajectories corresponding to the green curve in (E) (N = 1000, p = 0.2). (E) Analogously to (C) but varying the connection probabilities while keeping C = pN = 200 fixed. (F) Sample trajectories corresponding to the green curve in (G) (N = 200, C = 40). (G) Analogously to (C) but varying the number of synapses C while keeping N = 200 fixed. Note that the mesoscopic theory (black solid line) is independent of C because the product Cw, which determines the interaction strength in the mesoscopic model (see, left panel of (A)), is kept constant. Parameters: μ^E/I = 24 mV, ${\Delta }_u^{E/I}=2.5$ mV and θ^E/I(t) ≡ 0 (no adaptation).