Tracking the evolution of 3D gene organization demonstrates its connection to phenotypic divergence

Abstract

It has recently been shown that the organization of genes in eukaryotic genomes, and specifically in 3D, is strongly related to gene expression and function and partially conserved between organisms. However, previous studies of 3D genomic organization analyzed each organism independently from others. Here, we propose an approach for unified inter-organismal analysis of gene organization based on a network representation of Hi-C data. We define and detect four classes of spatially co-evolving orthologous modules (SCOMs), i.e. gene families that co-evolve in their 3D organization, based on patterns of divergence and conservation of distances. We demonstrate our methodology on Hi-C data from Saccharomyces cerevisiae and Schizosaccharomyces pombe, and identify, among others, modules relating to RNA splicing machinery and chromatin silencing by small RNA which are central to S. pombe's lifestyle. Our results emphasize the importance of 3D genomic organization in eukaryotes and suggest that the evolutionary mechanisms that shape gene organization affect the organism fitness and phenotypes. The proposed algorithms can be utilized in future studies of genome evolution and comparative analysis of spatial genomic organization in different tissues, conditions and single cells.

INTRODUCTION

In recent years, it has become evident that the genomic architecture and thus the 3D organization of genes in the genome is far from random (1–3). A number of recent studies have demonstrated that a relation between genes’ function and expression and their 3D organization exists (4–10). Analyses in eukaryotes of Hi-C data, measuring the 3D conformation of chromosomes (9), have revealed relations between genes’ organization and their co-expression (6,7,11) and TF binding sites (8,12). In addition, genes encoding interacting proteins, that form protein complexes and genes along the same pathway have been shown to be co-localized in 3D in human (10). Chromosomes’ 3D conformation has been shown to be related to tissue-specific regulation (13,14), and disruptions in this structure have been linked to a number of diseases (15,16), including the development of cancer (17,18).

Previous results have implied that 3D organization, function and expression co-evolve (4). However, almost all studies to date have analyzed one organism. Recent studies that analyzed more than one organism have analyzed each of them independently from others (3,4,19–21). For example, some degree of conservation of 3D organization has been shown between mouse and human genomes (4,20), and between Saccharomyces cerevisiae and Schizosaccharomyces pombe (4). The relation between the two fungi has been utilized to improve 3D reconstruction by integration of S. cerevisiae and S. pombe Hi-C maps (19). A comparative study of topological associated domains (TADs) between four mammals has revealed that conserved CTCF binding sites are enriched at TAD boundaries and that divergent CTCF binding between species is correlated with divergence of internal domain structure (21). Chromosome conformation and genes’ 3D positioning have been linked to gene expression regulation (4,9), thus divergence in gene expression is expected to be reflected in 3D gene organization (21). Recently, tools for studying differential Hi-C contacts have recently been proposed, and applied to the study of genomic organization in a cancer cell line (22,23), but to the best of our knowledge differential 3D organization has yet to be studied between organisms in gene resolution.

Here, we propose a novel framework for studying 3D gene organization across species using a unified multi-organism model representing the Hi-C data of both organisms (Figure 1). We apply it to the study of two fungi—S. cerevisiae and S. pombe, estimated to have diverged up to 1000 million years ago (24). The paper is divided into two major parts: an introductory section about global organization trends between the two species, and a major part about detection and analysis of spatially co-evolving orthologous modules (SCOMs) of gene families. We show that global trends of conservation as well as divergence exist between the fungi, that are coordinated with conservation and divergence of expression, codon usage patterns and protein interactions. We propose an algorithm for detecting modules of orthologous gene families that co-evolve in their 3D organization, and suggest various classes of SCOMs that can be detected via this method. Finally, we demonstrate that the detected modules are related to biological functions that have been conserved or diverged between the two species. These results provide a first look on how gene organization evolves in 3D.

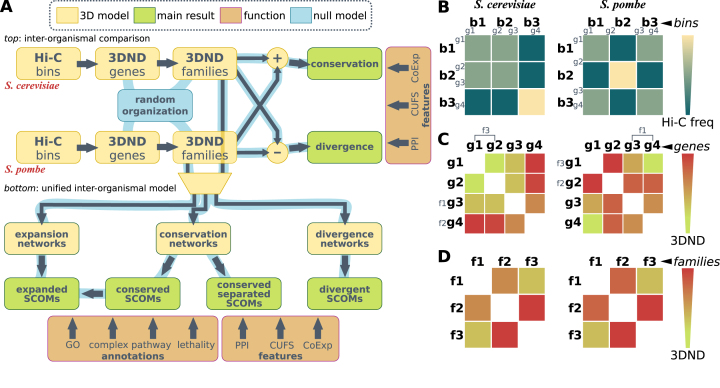
Figure 1.

Research plan. (A) Flow chart depicting the analysis pipeline. Component types (model, result, function, null model) are denoted by color. Top: representing 3D network distances (3DND) between orthologous families in each organism (data in bold and coordinates in regular font); analysis of conservation and divergence of organization vs. functional features. Random genomic organizations are generated and passed down the pipeline to obtain an empirical p-value for each result. Bottom: a unified network analysis of conservation and divergence of gene families; detection of spatially co-evolving ortholgous modules (SCOMs) and their analysis vs. functional annotations and features. Random genomic organizations are passed down the pipeline as well. (B) An illustration of the preparation of an inter-organismal model, including the first 3 steps shown in panel (A) (for network and SCOM illustrations see Figures 2–5). Normalized Hi-C frequency/probability matrices containing three bins are shown for S. cerevisiae (left) and S. pombe (right). Chromosome conformation is different in each species, and gene distribution (four genes marked) is different. (C) Continuation of the procedure in panel (B). Hi-C network distance matrices after transformation to gene coordinates are shown for the two organisms. Three orthologous families (with different structure/location) are marked. (D) Continuation of the procedure in panel (C). Distance matrices after transformation to family coordinates are shown for the two organisms. Despite differences in conformation, gene location and family structure, the resulting distances are conserved. These distances are utilized to generate the various networks, such as the conservation network.

MATERIALS AND METHODS

Genome sequence and annotation

Genome sequence and annotations were obtained from Ensembl (25) (S. cerevisiae R64-1-1, Ensembl release 78; S. pombe ASM294v2, Ensembl genomes release 26).

Co-expression

We utilized microarray data obtained from the Gene Expression Omnibus (GEO), including 494 samples from S. cerevisiae and 198 samples from S. pombe from various conditions (Supplementary Table S8). Each sample was normalized to have a mean of 0 and variance of 1 using Gaussian quantile normalization over genes’ values. Finally, Spearman's correlation was computed between the expression profiles of all pairs of genes. Additional protein abundance data was obtained from PaxDB (26,27) (S. pombe: Marguerat Cell 2012; S. cerevisiae: GPM Oct 2012; accessed 5 February 2016).

Hi-C data preparation

Hi-C data for S. cerevisiae (5) (SRX017804-5, SRX017809-10) and S. pombe (6,28) (SRX023134-5, SRX533435-6) was obtained from the Sequence Read Archive (SRA) (see also Supplementary Note 1 for an analysis of variance and noise in the datasets). We used an iterative mapping method to map the paired-end reads, as previously proposed (20) with minor modifications: Unique alignments to the genomes for the two read ends were generated using Bowtie 1.1.1 (29). In each iteration, a larger part of the read was considered for alignment in the range of [20 bp, 75 bp] (or bounded by the sequenced read length) with steps of 5 bp. The accepted error was proportional to the alignment length 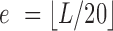(bowtie parameters: ‘-v {e} -3 {t} -m 1 –strata –best’ where {t} is the part of the read that was trimmed and {e} the acceptable error). We pooled the reads into their corresponding restriction fragments, and filtered reads that were either: more distant from the restriction site than the experiment's molecule length; aligned to restriction fragments <100 bp or >100 kb; both ends mapped to the same fragment or to adjacent fragments facing one another; single-side reads; or redundant reads (identical sequence). Finally, we pooled the fragment-based map into uniformly spaced bins in 10 kb resolution. We then used an iterative correction approach to reduce biases in the resulting maps, as previously proposed (20). Interactions in a range smaller than 20 kb were discarded (self and adjacent bins). Bins within the bottom 2% according their coverage (total reads) were discarded. Twenty iterations of correction were performed, by normalizing all contacts frequencies 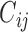between bin i and bin j by dividing by , where 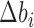is the deviation of the bin's coverage from the expected mean coverage of all N bins, 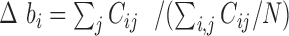. Each replicate (for a total of four per organism) was corrected separately and weighted equally to generate an aggregated (averaged) map. Finally, we iteratively normalized the columns and rows to have a sum of one by alternating between columns and rows until reaching a symmetric matrix (30), thus generating a normalized Hi-C map of contact frequencies / probabilities between each bin and all other bins (Figure 1B).

Hi-C network

Hi-C maps were then utilized to construct a network with orthologous families as its nodes. First, we constructed a genomic network, with its nodes being the binned coordinates produced in the data preparation step above. Edges in the network were set to be –log(p_ij), where p_ij are the normalized contact frequencies / probabilities between Hi-C bins, and shortest network distances between all node pairs were computed (3D network distance, 3DND). The resulting distances between pairs of bins can be interpreted as the maximum-likelihood of observing the two regions in spatial proximity. Second, we constructed a gene network, by mapping genes to their nearest bins and applying a bi-linear interpolation of the distances: Given a matrix of distances in bin coordinates we wish to compute the distance matrix in gene coordinates. For each gene 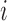, we define its adjacent bin 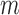as the Hi-C bin that its mid-point is downstream and closest to the mid-point of the gene. We define 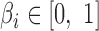to be the distance to the adjacent bin divided by the size of bins in the map (10kbp). For a pair of genes 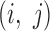that are adjacent to bins 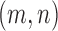, respectively, the distance between them is then given by: . 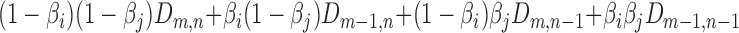The process is illustrated in Figure 1C and the resulting maps are given in Supplementary Figure S1. Finally, we constructed a universal network by averaging the distances between sets of genes in all pairs of orthologous families as described below.

A total of 9999 random networks were generated for computing empirical P-values (p_e) by permuting the locations of genes in the gene network (prior to the transformation to orthologous families). To retain many of the properties of the model (e.g. the distribution of distances, the number of genes in each chromosome), the nodes and edges of the network remained unchanged, but gene IDs (labels) were shuffled across the genome. Additional 9999 random networks were generated by cyclic-shifting gene IDs within each chromosome, so that the positions of genes are uniformly distributed but the adjacent neighbors of each gene on the chromosome remain identical, thus approximately preserving the linear distances between genes (4). All steps of the analyses were performed on the random networks, similarly to the real data, in order to obtain a sample from the empirical null distribution.

Normalized family values

To enable comparison of values across organisms we utilized the eggNOG v4.1 (31) set of orthologous families across eukaryotes (euNOG). We included 2716 families with identified orthologs in the budding yeast and fission yeast (Supplementary Table S9). Given a feature (e.g. co-expression coefficients) between pairs of genes, the value for a pair of families 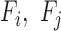was calculated using the average over all pairs of genes in 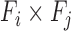(Figure 1D). Finally, all values were normalized to have mean 0 and variance of 1 using Gaussian quantile normalization for each organism independently.

Empirical P-value

All reported P-values are empirical (p_e), unless stated otherwise. 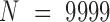samples were drawn from the empirical null distribution by repeating the analysis in question on data from the permuted genomes above, and obtaining theoretical / asymptotic P-values 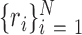from the null samples (e.g. the result of Wilcoxon's rank-sum test, the result of a hyper-geometric enrichment test, etc.). We used the following estimator for the empirical P-value based on 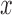, our observed test result: 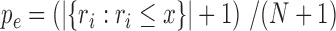(32). That is, we count the number of null samples where the obtained test result was more / as significant as the one observed.

In the case of functional enrichment, we performed multiple correction similarly to (33). We repeated functional enrichment for the modules detected in the permuted genomes (as described above), and compared the distribution of the minimal P-value obtained for every term across all SCOMs in the sample to the hyper geometric P-value obtained for that term in the observed network. We computed two additional P-values that are given in Supplementary Tables S2, S4, S5, S7: a hyper-geometric P-value, adjusted for FDR (p_hg-adj) (34); and an empiric P-value based on the cyclic-shifted networks defined above (p_cyc). We demanded that 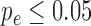and 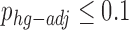for the reported terms. It can be seen that in general p_e tends to be stricter than p_hg-adj and more permissive than the heavily constrained p_cyc. While p_cyc was not used to filter the enriched terms, it is interesting to study, and can provide a control for the level of 1D (linear) clustering in the respective set of genes (how close the genes are linearly on the genome).

Conservation network

We constructed a network of orthologous families with conserved relative distances. To this end, we considered pairs of families that are in the top-k distances (red edges in network G^r(V, E^r)) or bottom-k distances (green edges in network G^g(V, E^g)) in both organisms. We analyzed the sensitivity of these networks and SCOM detection to selected parameters in Supplementary Note 2 and Supplementary Figure S2.

Divergence network

We constructed a network of orthologous families that changed their relative 3D position between organisms. To this end, we considered pairs of families that are in the top-k distances in one organism, and bottom-k in the second organism (k = 15%). Two networks were constructed according to the direction of repositioning. Binary edges were set in the S. cerevisiae network G^SC(V, E^SC) between all node pairs that are in the top-k in S. pombe and bottom-k in S. cerevisiae (i.e. nodes that moved towards one another) and vice versa in the S. pombe network G^SP(V, E^SP).

Expansion network

To consider the 3D neighborhood of SCOMs in each organism independently, we constructed two binary networks as follows. A family network was constructed by connecting the families with the bottom-k distances (k was selected so that the edges-to-nodes ratio will be identical to the conservation network). A gene network was constructed by connecting the genes with the bottom-k distances (k selected according to the same rule).

Spatially co-evolving orthologous modules (SCOMs)

We defined four classes of spatially co-evolving orthologous modules (SCOM) based on the divergence, conservation or expansion networks: (i) Conserved SCOMs containing families that retained their co-localization. (ii) Divergent SCOMs comprising of families that became co-localized in 3D in one organism. (iii) Expanded SCOMs containing genes in the 3D neighborhood of a conserved core. (iv) Conserved SCOMs containing two sets of families, such that each set is co-localized and conserved in 3D, but the two sets are distinctly separated in 3D. These four classes can be translated to the graph theoretical problem of finding heavy/dense subgraphs within the respective networks, that is, subgraphs that have an unusually high number of edges between the module's families. We used an approach similar to previous studies in order to solve these four problems (35,36), as detailed below.

Specifically, we scored candidate subgraphs according to the following functions, respectively, for each of the SCOM classes. For detecting gene re-organization in divergent SCOMs (class 2), we considered the divergence network G^SC(V, E^SC) of co-localizing families in one organism, e.g. S. cerevisiae. To quantify how unusually high the number of edges is within a SCOM, we derived the log-odds score comparing two hypotheses: under the SCOM hypothesis, every pair of genes in the module V_i is co-localizing with a high probability α (selected to be 0.9) where an edge is present (and a low probability 1 – α when it is absent), independently of all other gene pairs. The likelihood of a module V_i is thus 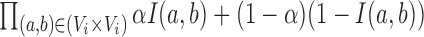, where 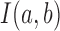equals 1 if there exists an edge in E^SC between nodes a and b. Under the null hypothesis, every pair 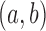is connected with probability 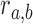, representing the chance of observing this interaction at random. We estimate 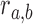by considering additional, independently drawn 1,000 random divergence / conservation / expansion networks (according to SCOM class) and computing the probability of observing an edge between nodes a and b (unobserved edges were assigned with probability 10⁻⁴). The log-odds score is then:

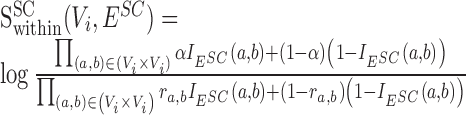(1)

A similar function 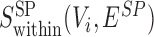can be defined for the S. pombe divergence network G^SP(V, E^SP). We applied the same method to score conserved SCOMs (class 1), by searching for dense subgraphs in the conservation network G^g(V, E^g) according to the corresponding function 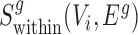. For expanded conserved SCOMs (class 3), we utilized the two expansion networks described above.

Finally, for conserved separated SCOMs (class 4) we require enrichment of green edges within two disjoint sets of conserved co-localized nodes (V_i, V_j), |V_i|,|V_j|>2, which can be achieved using the sum of two scoring functions, 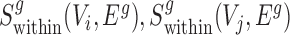. In addition, we require enrichment of red edges between the two sets, which can be achieved by defining a new additional scoring function 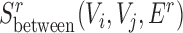as follows:

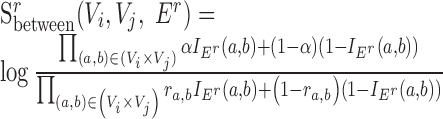(2)

The total score for a class 4 SCOM is thus .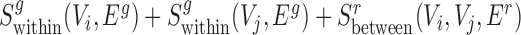

Dense subgraphs search

We employed a heuristic optimization algorithm to maximize the score of SCOMs similarly to previous studies (35,36). We begin the optimization from seeds comprising of small sets of nodes with enriched edges, and expand them iteratively. The seeding was done using an approximation for the densest subgraph (37) with weights between nodes corresponding to the scoring function defined above. Finding the densest subgraph is followed by the removal of all its nodes from the graph and repeating the process to find the second-densest subgraph etc., until no nodes are left. Seeds with log odds-ratio score <20 were discarded. We then tried to maximize the score of modules iteratively, trying in each iteration to add a new node and remove an existing node from the module, if either step increases the objective and satisfies the constraints below. We modified modules in random order, and stopped the process when no additional improvement could be achieved. Node addition was subject to the constraint that the module does not exceed the maximal allowed size (30 nodes) and deletion was bounded by the minimal module size (five nodes for conserved/divergent SCOMs, two nodes for each submodule of the separated SCOMs). In addition, the allowed maximal overlap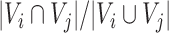 with other modules was 20%.

For expanded SCOMs (class 3), we used the output of (class 1) as seeds (converted to gene coordinates when using the gene expansion network defined above), increased the maximal size to 100, and removed the overlap constraint to allow SCOMs to expand. We did not allow deletion of nodes to retain the conserved core of the SCOM. Finally, for conserved separated SCOMs (class 4) we used the same approach and employed the combined score function from the previous section. However, seeding was done by pairing disjoint dense seeds in G^g(V, E^g) that in addition have the highest 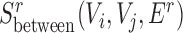score.

Modules were visualized in Cytoscape 3.3.0 (38) using the edge-weighted spring embedded layout with minimal adjustments for readability. Although not guaranteed, this layout tends to place genes from the same family in proximity, as well as any other node that shares the same interactions with the rest of the nodes in the graph.

Functional enrichment

We utilized annotations of GO terms (accessed 04/09/15) obtained from SGD (39) and Pombase (40) (in addition, we mapped GO terms to generic slim definitions (41)), S. cerevisiae pathways obtained from Wiki Pathways (accessed 29 April 2016) (42), and essential genes among one-to-one orthologs between the fungi (43) (Supplementary Table S11 in the paper). In order to utilize these annotations, we transformed nodes back from orthologous families to the organism's genes. We computed the hyper-geometric P-value for terms enriched within the modules and used them to calculate an empirical p-value as described above. The background set of genes was selected to be all the identified orthologs in the organism.

RESULTS

Genomes go through reorganization during evolution, including among others exchange of DNA within and between chromosomes (44,45). In addition, changes in the nucleotide composition of the chromosomes affect their conformation the 3D positioning of genes (21,46). Concurrently, genomes evolve and adapt the function and expression of genes to new environments. If indeed a strong relation exists between genes’ expression, function and their genomic organization, as has been previously suggested (4–10,19), we expect to see co-evolution between the two (4).

We propose, for the first time, an inter-organismal model based approach for Hi-C analysis in order to study the co-evolution of genes’ organization and their function (Figure 1). Our approach begins with Hi-C data measured independently in the two organisms, which is utilized to generate a model of gene-gene 3D distances, and transformed to universal coordinates of orthologous gene families. This enables direct large scale automatic comparison of pairs of distances between the fungi, and their relation with various functional features can be investigated (Figure 1A, top), such as the correlation coefficient between the transcription levels of pairs of genes (co-expression, CoExp).

In the second, central part of the paper (Figure 1A, bottom), we generate a number of networks that capture in a unified model the 3D evolutionary relations between gene families, and search them for various proposed classes of SCOMs. These modules are then analyzed using functional features, functional enrichment and the relevant literature.

Global evolutionary relation between genes’ function and their 3D organization

We utilized Hi-C measurements done in S. cerevisiae (5) and S. pombe (6,28) to construct a network of the 3D organization of orthologous families (Figure 1B, details in the methods section). We generated, for every pair of nodes in the network an estimation of their 3D network distance (3DND) in each organism as well as distance measures related to their function and expression.

We first observe that there exists a significant relation between the average 3DND of orthologous families across organisms and their average co-expression. We divided all pairs of families to seven equal-size fractions, with increasing average 3DND across organisms, and performed Wilcoxon's rank-sum test between adjacent fractions according to the distribution of co-expression coefficient for pairs of families within each fraction. Adjacent fractions showed significant difference, and that co-expression decreases with 3D distance (p_e = 10⁻⁴; 10⁻⁴; 2.5 × 10⁻³; 9 × 10⁻⁴; 0.0233; 0.1485; empirical rank-sum P-values ordered by increasing distance, details in the methods section). The observed relation reflects the fact that the relative distances between many pairs of genes and their functional relations are both conserved between the two fungi, and that expression/functionality correlates/relates to 3D distance. Furthermore, when considering pairs of genes with conserved 3DND between them, i.e. that they are within the bottom 25% of distances in both organisms, they were found to have higher co-expression than pairs that were not conserved (p_e = 10⁻⁴, empirical rank-sum P-value). Similarly, conserved distant genes showed lower co-expression than non-conserved ones (p_e = 0.0406) (see also Supplementary Figure S3).

Next, we asked whether changes in the organization of genes are also reflected in changes in their co-expression. We repeated the above test for seven equal-size fractions with increasing difference in 3DND between the budding yeast and the fission yeast, and compared the difference in co-expression between fractions. Adjacent fractions showed significant difference and an inverse relation, i.e. that co-expression increases in the organism where families have decreased their distance (p_e = 10⁻⁴; 10⁻⁴; 0.0126; 0.0229; 1.1 × 10⁻³; 10⁻⁴, empirical rank-sum P-values, ordered by increasing 3DND difference, from pairs that co-localized in S. pombe in one end, to pairs that co-localized in S. cerevisiae). Thus, pairs of genes that decreased their spatial proximity during evolution also tended to increase the correlation between their expression patterns. We obtained similar relations between changes in 3DND and other features, such as protein–protein interaction network distances, and a codon-usage based metric for comparing the functional similarity of genes (4) (see Supplementary Note 3 and Supplementary Figure S4).

These results demonstrate that spatial proximity is connected to fundamental organismal phenotypes; thus, developing approaches to detect various spatial gene organization signals, as described in the next sections, is an important mission.

Spatially co-evolving orthologous modules

In order to study more closely the reported large-scale patterns of co-evolution between gene 3D organization and functionality, we propose a novel method for inter-organismal study of genomic organization. Our method is based on the identification of spatially co-evolving orthologous modules (SCOMs), that is, sets of genes that show significant coordinated three-dimensional reorganization or conservation between two organisms. We propose four classes of SCOMs, describe algorithms for finding them efficiently, and show that they correspond to biologically meaningful modules of co-evolving genes.

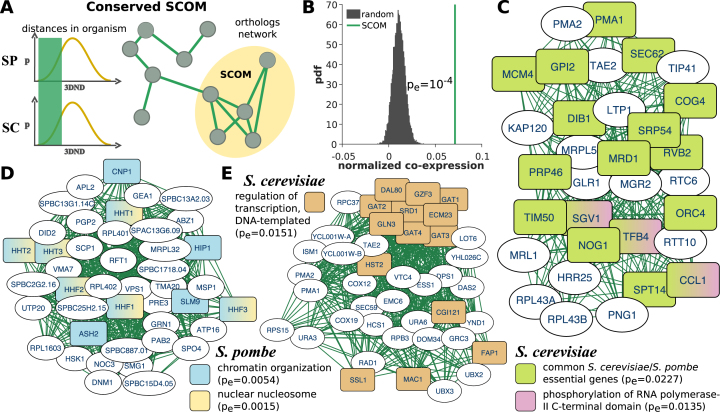
We begin by describing the simplest class of conserved SCOMs. These are modules of genes that maintained spatial proximity across evolution (Figure 2A). In order to identify them we constructed a network that describes conserved 3DND between organisms by setting an edge between a pair of orthologous families if their 3DND is below a certain threshold in both organisms (the bottom 15% was selected). We then defined conserved SCOMs as dense / heavy subgraphs in the network that are enriched with edges between the module's genes, denoting distance conservation. We scored each SCOM by comparing the observed edges to the probability of observing them according to a null distribution generated from permuted networks. A formulation of the problem and an algorithm for solving it appear in the methods section. The resulting SCOMs (Supplementary Table S1 includes the complete sets of genes) show higher co-expression within SCOMs compared with random modules (p_e = 10⁻⁴, Figure 2B). In addition, they scored significantly higher than SCOMs detected in randomly permuted genomes (p_e = 0.001), and covered a larger fraction of the genome (83% of families, p_e = 10⁻⁴). The average linear distance (in base pairs) between genes in the conserved SCOMs was 214 kb in S. cerevisiae and 611kbp in S. pombe, and they also contained genes from different chromosomes. These results suggest that the SCOMs have a biological meaning, and that they are able capture long-range 3D interactions between genes.

Figure 2.

Conserved SCOMs. (A) Illustration of a conserved SCOM based on S. cerevisiae (SC) and S. pombe (SP) distances. Edges in the network denote pairs of families that have similar distances (bottom-k) in both organisms. (B) Normalized coefficient of co-expression between conserved SCOM genes is significantly higher compared with co-expression in random SCOMs (permuted genomes, empirical P-value). (C–E) Examples for conserved SCOMs. Nodes are genes, and interactions were transformed from the conserved network of orthologous families (the gene lists / details appear in Supplementary Table S1). Significant functions are highlighted. Additional modules appear in Supplementary Figure S5.

We performed functional enrichment within conserved SCOMs, and found enriched functional annotations in 84 out of 152 detected modules in the two yeasts (Supplementary Table S2 contains the complete list). Specifically, we found that essential genes (determined by knockout screens (43)) that are common to both organisms are over-represented in a conserved SCOM (p_e = 0.0227, Figure 2C). Several chromatin-related protein complexes appear in SCOMs, such as histone acetyltransferase over-represented in two SCOMs, p_e1 = 0.0153 and p_e2 = 0.0018; nuclear nucleosome genes, p_e1 = 0.0180 and p_e2 = 0.0015 (Figure 2D; with protein abundance in the top 5% of all genes, and genes are significantly co-expressed, average r = 0.43, p_e = 0.0129, details in the methods); nuclear telomeric heterochromatin genes, p_e1 = 0.0213 and p_e2 = 0.0079); and the GO term chromatin organization (p_e = 0.0054) (Figure 2D). A number of SCOMs relate to fundamental stages of gene expression—transcription (e.g. regulation of transcription, p_e1 = 0.0363, p_e2 = 0.0151, Figure 2E; TFIID complex, p_e = 0.0385; termination of RNA polymerase II transcription, p_e = 0.0283; and phosphorylation of RNA polymerase II C-terminal domain, p_e = 0.0135, Figure 2C) and translation (e.g. cytoplasmic translation, p_e = 0.0416, Supplementary Figure S5, co-expressed with r = 0.58, p_e = 5×10⁻⁴; ribosomal small subunit biogenesis, p_e = 0.0469, co-expressed with r = 0.42, p_e = 0.0145; regulation of translational fidelity, p_e = 0.0342; tRNA methylation, p_e = 0.0269). Furthermore, multiple modules are associated with ion transport and homeostasis (ion transport, p_e1 = 0.0143 and p_e2 = 0.0270; cellular copper ion homeostasis, p_e = 0.0181; and cellular ion homeostasis, p_e = 0.0493, Supplementary Figure S5). For example, the latter set contains, among others, the S. cerevisiae family of CTH1 and CTH2 (TIS11), related to regulation of iron metabolism at the post-transcriptional level (47), and a family of glutaredoxins (GRX3-4) which regulates iron metabolism at the transcriptional level (48). Glutaredoxins (including GRX3-5) also take part in cellular response to chemicals (significantly represented in the same module) by protecting the cell from oxidative damage. Finally, multiple conserved modules are enriched with mitochondrial terms (e.g. mitochondrial membrane, p_e = 0.0291; positive regulation of mitochondrial translation, p_e1 = 0.0012, p_e2 = 0.0011, Supplementary Figure S5; mitochondrial translational initiation, p_e = 0.0411; and mitochondrial inner membrane peptidase complex, p_e = 0.0061). While Hi-C measurements are affected by the 1D proximity of genes on the DNA, and our model specifically does not attempt to avoid adjacencies between genes (which are relevant to our study) in SCOMs, many of the enriched terms also pass our control for 1D proximity (details in the methods section, and in Supplementary Table S2).

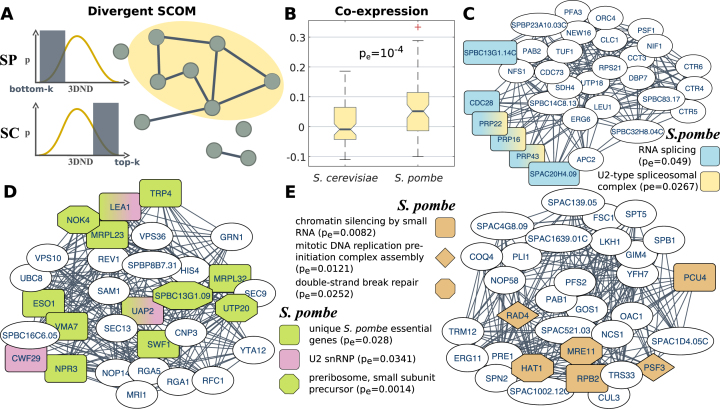
Divergent SCOMs link re-organization to phenotypic divergence

Next, we propose a second class of divergent SCOMs. These are modules of genes that have undergone large coordinated changes in their 3D organization and are now co-localized in only one of the organisms (and distant in the second organism, Figure 3A). In order to identify them we constructed a network describing divergent pairs of genes according to their 3DND, i.e. by setting an edge between genes if they are in the top-k distances in one organism and also in the bottom-k distances in the other organism (k = 15%). Divergent SCOMs are dense subgraphs in this network, and can be found using the same algorithm. The number of detected modules (Supplementary Table S3) was higher than in permuted genomes (S. cerevisiae: 91 p_e = 0.034; S. pombe: 81 p_e = 0.061). We analyzed the change in co-expression of genes within the modules by comparing co-expression between organisms (Figure 3B). We expect, based on our global analysis, that gene expression similarity between genes that co-localized in S. pombe, e.g. will be higher in S. pombe compared with the similarity between their orthologs in S. cerevisiae (p_e = 10⁻⁴, empirical sign-rank P-value). We performed functional enrichment within the modules and found 46 and 42 modules containing significantly over-represented functions in S. pombe and S. cerevisiae, respectively (Supplementary Table S4). In a similar manner to conserved SCOMs, we found genes that are uniquely essential to the fission yeast, enriched in a divergent SCOM that co-localizes only in S. pombe (p_e = 0.0280, Figure 3D). Among processes that changed their 3D organization between the species, we found that genes related to RNA splicing (p_e = 0.0490, Figure 3C) co-localize in S. pombe, but do not in S. cerevisiae. These genes include the RNA helicases PRP16, PRP22, PRP43, CDC28, SPAC20H4.09, involved in spliceosome assembly/disassembly, and the RNA binding SPBC13G1.14c. This re-organization is expected, since the transcriptome of S. pombe contains 5061 introns, including over 1000 multiple-intron genes, whereas S. cerevisiae has only 327 introns and nine multiple-intron genes. In addition, three SCOMs are associated with the U2 type spliceosomal complex (p_e1 = 0.0028, p_e2 = 0.0267, Figure 3C) and U2 snRNP (p_e3 = 0.0341, Figure 3D). Thus, the 3D organization of the SCOMs reflects the major role of splicing in this organism. Specifically, it is possible that the selection for the higher co-localization of splicing genes in S. pombe enables better/optimized regulation of splicing, which is specifically more important when the number of introns is significantly higher.

Figure 3.

Divergent SCOMs. (A) Illustration of a divergent SCOM. Edges in the depicted S. pombe network denote pairs of families that significantly co-localized compared with their distances in S. cerevisiae (moved from the top-k to the bottom-k distances). (B) Comparison of the normalized co-expression coefficient within divergent modules where genes co-localized in S. pombe, distributions for the module genes shown in each of the organisms (empirical sign-rank P-value). (C–E) Examples for divergent SCOMs. Nodes are genes, and interactions were transformed from the conserved network of orthologous families. Significant functions are highlighted. Additional modules appear in Supplementary Figure S6.

One of the striking differences between the budding and fission yeast is that the former has a single large vacuole, taking up a quarter of the cell volume, while the latter has multiple small vacuoles (49). Most of the related genes have identified orthologs in the two species; however, this phenotype is reflected in their organization and the co-localization of vacuolar membrane gene families in S. cerevisiae (p_e = 0.0161, Supplementary Figure S6). It is also known, that S. pombe vacuoles can dynamically change their number by fusing in response to environment by the HOPS complex (49). In accordance with this trait, we found the vacuole fusion process enriched in S. pombe (p_e = 0.0483, co-expressed with r = 0.61, p_e = 0.0382, Supplementary Figure S6), and specifically genes of the VTC complex involved in this process (50). In addition, membrane fusion genes were significantly represented in S. pombe divergent SCOMs (p_e = 0.0327), including the vacuolar sorting protein VPS33 (a subunit of HOPS, and mutants where it is missing exhibit severe morphological defects) (49), as well as additional vacuolar genes such as VPS1 (vacuoles carrying no or impaired Vps1 were shown to be fusion-deficient in S. cerevisiae) and the SNARE-protein encoding gene SEC22 (49,50).

The sexual behavior of the two yeasts is also largely different. The mostly-diploid S. cerevisiae sporulates in response to starvation and then immediately conjugates, while the mostly-haploid S. pombe conjugates in response to starvation and then immediately sporulates back to haploid state (51). Thus, it is expected that the two species have different divergent SCOMs associated with response to starvation (S. cerevisiae: p_e = 0.0198; S. pombe: p_e = 0.0102, genes co-expressed with r = 0.27, p_e = 0.0445, Supplementary Figure S6). S. cerevisiae mates readily, and haploid cells are capable of switching their mating type in order to maximize chance of diploid formation (52). In accordance with this trend we found enriched in S. cerevisiae SCOMs the mating-pheromone response pathway (p_e = 0.0186, co-expressed with r = 0.52, p_e = 0.0155; e.g. the genes GPA1, a subunit of the G protein, and STE2, a receptor for the alpha-factor pheromone that interacts with the pheromone and G protein (53)), as well as the MAPK signaling pathway (p_e = 0.0113, Supplementary Figure S6; e.g. the genes STE4, STE7, encoding kinases that interact with the S. cerevisiae-unique FAR1, which arrests the cell cycle of haploid cells in response to pheromone (51)). The fission yeast is known to be resistant to lethal effects of both UV and ionising radiation, when compared to S. cerevisiae and most other eukaryotes (54). We found in S. pombe divergent SCOMs associated with DNA repair (p_e = 0.0376, Supplementary Figure S6; e.g. the genes POL4, PLI1, NTH1, PSO2, PSM3, CDC17, ADL1), and with double-strand break repair proteins (p_e = 0.0252, Figure 3E). Finally, S. pombe has unique RNAi machinery for chromatin silencing (55), we therefore expected to detect the biological process chromatin silencing by small RNA enriched in a divergent SCOM (p_e = 0.0082; e.g. the RNA polymerase II complex subunit RPB2 which mediates RNAi-directed chromatin modification (56), and PCU4 which mediates heterochromatin formation (57), Figure 3E). In addition, we found chromatin silencing at centromere outer repeat region enriched as well (p_e = 0.0063; e.g. the genes HST2, EPE1).

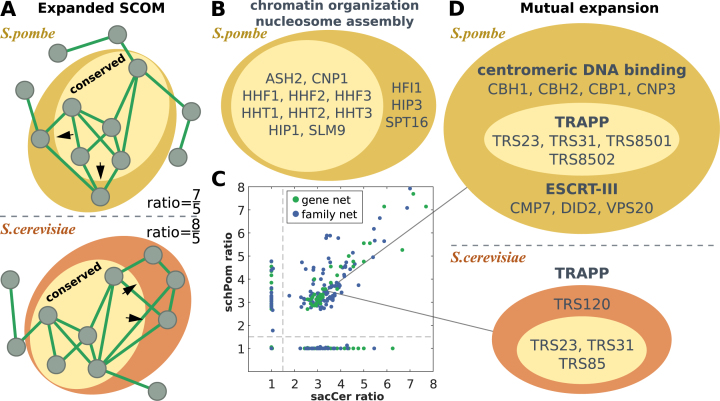
Species-specific expansion of conserved SCOMs

We propose another approach to study re-organization, by tracking changes in the surrounding neighborhood of conserved SCOMs. To this end we considered a third class of SCOMs, based on the 3D environment of every conserved SCOM, in each of the organisms independently. We attempted to expand the conserved core of such SCOMs until reaching a maximal size for the co-localized set. We separately considered expansion by addition of families, as well as expansion by addition of genes (including genes lacking identified orthologs in the other species, Figure 4A). For example, one of the conserved SCOMs from above, that relates to chromatin organization and nucleosome assembly, has expanded in S. pombe to include additional families with the same functionality (p_e1 = 0.0089, p_e2 = 0.0027), which may partially be related to the different nucleosome positioning patterns observed in this species (58) (Figure 4B). Our results indicate that many of the detected conserved SCOMs are part of a larger, non-conserved, organism-specific module; i.e. that the core greatly (up to 8-fold) expanded in one of the organisms, while few modules were confined to the small conserved core in both organisms. In many of the cases, SCOMs considerably expanded in both organisms (Figure 4C). Similar modules expanded according to the same (organism-specific or not) pattern via family expansion and via gene expansion (P < 10⁻⁹, theoretical hyper-geometric test). Enriched functions within expanded SCOMs that increased their size only in one organism (see also Supplementary Table S5) include, for example, families in S. cerevisiae related to cellular bud site selection (p_e = 0.026), which is unique to S. cerevisiae and establishes cell polarity early in the cell cycle compared with S. pombe (52). The same module also contains families related to microtubules (beta-tubulin binding, p_e = 0.0255), the latter take part in nucleus migration to the bud neck to prepare for cell division (59). In modules expanded with genes, we find positive regulators of pseudohyphal growth (p_e = 0.0225), which is triggered by different signaling pathways in the two species (60), and genes related to cell wall structure (p_e = 0.0259). Similarly, in modules that expanded specifically in S. pombe we also find genes related to the cell wall (p_e = 0.0234), that could possibly reflect the different cell wall composition of the two yeasts (61,62). We also observe in this organism an expansion towards genes related chromatin silencing at centromere outer repeat region (p_e = 0.0191, also appearing in a divergent SCOM above), while the budding yeast's centromeres do not contain such repeats and aren't silenced (55). It has been suggested that transcription patterns of purine metabolism changed pre- and post-whole genome duplication in the fungi phylogeny, and specifically between fission and budding yeast (63), and indeed we find it enriched in the fission yeast (p_e = 0.0369). S. pombe-specific expanded modules also contain, among others, a subset of families and genes related to positive regulation of G2/M transition (p_e1 = 0.0111, p_e2 = 0.0464), a checkpoint that plays a greater role in this organism (51), within a larger set of cell cycle regulating genes (p_e = 0.0246).

Figure 4.

Expanded conserved SCOMs. (A) Illustration of the expansion of a conserved SCOM in each organism individually. The light area shows the conserved core of the SCOM while the dark area shows families/genes added to the expanded SCOM in each of the fungi. (B) Example for significant GO terms that expanded within a fission yeast SCOM by including additional related families. Additional results appear in Supplementary Table S5. (C) Expansion ratios of the conserved SCOMs in one organism vs. the other, for expansion across the gene network and the family network (details in the methods section). (D) Examples for significant GO terms in a SCOM which expanded (differently) in both species.

Conserved module cores may evolve in different directions in each species (Figure 4A), perhaps reflecting different interfaces and interactions that evolved between conserved functions and other cellular functions. Recently, it was shown that in the fission yeast, unlike the budding yeast, the ESCRT-III complex regulates spindle pole body (SPB) duplication (64). Here we found that ESCRT-III is enriched in the same expanded SCOM (p_e = 0.0399) along with centromeric DNA binding families (p_e = 0.021, including kinetochore and SPB genes CBH1, CNP3). The conserved core of this SCOM contains families of the TRAPP protein complex (p_e = 0.0017) (Figure 4D). Interestingly, ESCRT-III has also been implicated to be directly involved in cytokinesis in many organisms including S. pombe, but not in S. cerevisiae yet (65). Recently, TRAPP-II has been shown to participate in cytokinesis too in S. pombe (66). Meanwhile, the same conserved module in the budding yeast expanded in a different direction to include additional TRAPP-II genes (p_e = 0.0343). Families related to arginine biosynthesis were enriched in seven different (mutually exclusive) SCOMs that expanded in both organisms (p_e = 0.0128–0.0332), a metabolic process which has been noted to comprise of proteins with considerably different protein half-lives in S. cerevisiae and S. pombe (67), possibly leading to divergence in their regulation. S. cerevisiae can take up sterol under low oxygen when biosynthesis is compromised, unlike S. pombe (68), and indeed we found S. cerevisiae genes related to sterol homeostasis in mutually expanded SCOMs (p_e = 0.017). S. cerevisiae genes related to regulation and establishment of cell polarity appear in two modules that expanded in both organisms (p_e = 0.0268–0.0457), in addition to those reported above for S. cerevisiae-specific modules. Finally, families related to meiosis and conjugation are enriched for both fungi: S. cerevisiae genes and families appear in species-specific expanded modules (conjugation with cellular fusion, p_e = 0.0098; meiotic cell cycle, p_e = 0.0199) while S. pombe families and genes appear in mutually expanded modules (conjugation, p_e = 0.0060; meiotic cell cycle, p_e = 0.05; meiosis II: p_e = 0.0319). These results suggest that the spatial neighborhood of conserved SCOMs changes during evolution and reflects, in part, functional and regulatory shifts between the fungi.

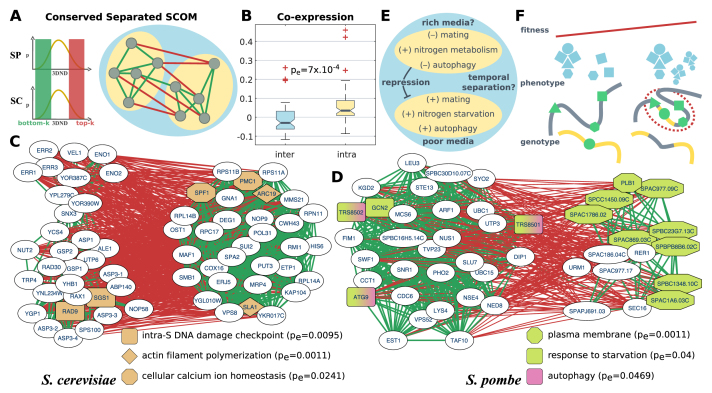
Conserved separated SCOMs can detect multi-module 3D architectures

Finally, to demonstrate the flexibility of our approach, we propose a fourth class of conserved and distinctly separated SCOMs. These are modules of families that maintained their spatial organization conserved, and contain two sets of co-localized genes that have been kept spatially separated across evolution (Figure 5A). For example, this class may capture cases where the genes in each of the sets are regulated in the same conditions in both organisms (this contributes to the co-localization of families in the two modules), but the nature of these two conditions is different in both organisms (this contributes to the dispersion of the two modules).

Figure 5.

Conserved separated SCOMs. (A) Illustration of a conserved separated SCOM. Edges in the network denote pairs of families that are either conserved and co-localized (bottom-k, green) or conserved and dispersed (top-k, red) in both organisms. (B) Comparison of the normalized co-expression coefficient within separated submodules versus between separated submodules. Boxplots show the distribution of the average value across organisms (empirical sign-rank P-value). (C–D) Examples for conserved separated SCOMs. Green edges denote conserved co-localization, while red edges denote conserved large distance (separation) between families. Significantly enriched functions are highlighted. (E) A diagram of known positive and inverse relations between biological processes and genes within the submodules of the separated SCOM in panel (D), along with hypotheses for the functionality of their separation. (F) Illustration of a hypothesized emerging SCOM. left: a new protein complex (blue), composed of genes (green) distributed across the genome (on the gray/yellow chromosomes), is formed and gives rise to new functionality. Due to limited regulation on the expression of the genes and the ratio between their products, the efficiency of complex formation is low. right: genome rearrangement (between yellow/gray chromosomes), as well as changes to the conformation of the chromosome, lead to co-localization of the genes, to tighter regulation on their co-expression and to an increase in the organism fitness (red trend line), thus promoting the formation of a new SCOM (red circle).

To this end, we introduce a second network of conserved distances, with edges between genes with 3DND above a certain threshold in both organisms (we selected the highest 25%). By combining the conservation networks of co-localized (bottom-k) and co-dispersed (top-k) genes, distinctly separated SCOMs can be identified. A formulation of the problem appears in the methods section. The resultant modules (Supplementary Table S6 includes the complete list) show increased co-expression within each submodule, compared with the co-expression between submodules (p_e = 7 × 10⁻⁴, empirical sign-rank P-value, Figure 5B). We detected enriched functions within each of the two submodules that the SCOMs comprise of (Supplementary Table S7). For example, genes related to S-phase DNA damage checkpoint according to S. cerevisiae annotations (p_e = 0.0095), including RAD9 (a central protein required for cell cycle arrest (69,70)), are distinctly conserved and separated from actin filament polymerization genes (p_e = 0.0011). This pair of genes is specifically involved in endocytosis (71,72), but was suggested also to play a role particularly at later stages of the cell cycle (cytokinesis) (73,74) (Figure 5C).

As another example, genes associated with response to starvation (p_e = 0.04) are distinctly separated from plasma membrane genes (p_e = 0.0011), including among others families of urea transporters (a source for nitrogen) and phospholypases (such as PLB1, implicated in the repression of S. pombe mating in nutrient-rich environment, and suggested to regulate the production of lipid second messengers along with other phospholipid/lipid-modifying enzymes) (75) (Figure 5D). In addition to the annotated response to starvation genes, the submodule also contains STE13, and indeed ste13 mutants fail to perform cell cycle arrest in response to nitrogen starvation (76). It has been shown that fission yeast chromosomes go through reorganization in response to nitrogen starvation to activate nitrogen-repressed genes (77). Such reorganization has yet to be reported in the budding yeast. Enriched in the same submodule are autophagy related genes in both organisms (p_e = 0.0167–0.0469). In S. cerevisiae, a relation between autophagy and response to nitrogen starvation has also been suggested (78). Mating in S. pombe is typically related to starvation, thus we expect genes that inhibit mating (such as PLB1) to be separated in 3D from the starvation response submodule. Interestingly, autophagy (and specifically ATG9) was shown be crucial for mating in a nitrogen depleted environment (79,80). The gene EST1 was also shown to increase mating efficiency (76). Similarly to mating, autophagy was shown to be repressed in rich media (with nitrogen transporters, possibly such as the ones in the counter submodule, hypothesized to take part in this regulation) (79). Indeed, we find that PLB1's expression is significantly anti-correlated with the autophagy related genes (average r = –0.26, p_e = 0.0054). We note that the basic machinery for autophagy is conserved between S. pombe and S. cerevisiae; however, in the latter autophagy is induced both by nitrogen as well as carbon depletion (79). Unlike S. pombe, S. cerevisiae goes first through sporulation in response to starvation, a process for which autophagy is also required (81). Figure 5E summarizes the aforementioned relationships and possible hypotheses for the inter/intra-submodule relations within this SCOM. The above studies suggest that one of the submodules is related to processes occurring in a nutrient-poor environment in both organisms—which may contribute to their conserved co-localization. Some of these genes are negatively regulated by genes in the other submodule, which also contains genes for nutrients transport—and may contribute to their conserved separation from the first submodule. Finally, the latter submodule contains genes that their proteins co-localize physically, which may contribute to their conserved co-localization in the genome.

DISCUSSION

Our results emphasize the importance of 3D genomic organization in eukaryotes and suggest that the evolutionary processes that shape the 3D organization of genes do not have a neutral effect on their functionality and expression pattern. We have previously shown a relation between 3D gene organization and codon usage, expression and function (4), and that 3D distances measured in S. pombe can be utilized to improve 3D genome reconstruction in S. cerevisiae (19); these results are supported by many additional studies in the field (5–7,9,11,46). Here we directly show that despite the great evolutionary distance between S. cerevisiae and S. pombe, and their different genomic organization, large-scale patterns of conserved 3D distances exist that are coordinated with genes’ co-expression. Furthermore, changes in 3D organization are also reflected in coordinated change in expression. Similar results using additional features such as a codon usage measure, CUFS (4) and PPI networks, appear in Supplementary Note 3 and Supplementary Figure S4. Here, we proposed a framework for detecting modules of gene families for which their 3D organization co-evolves (SCOMs) and demonstrated that modules representing conserved function/expression and organization can be detected, as well as re-organized modules where functional rewiring occurred to reflect the particular lifestyle of the organism.

Cellular processes can evolve in complex ways in their 3D organization, with parts of a process remaining conserved while other parts diverging and reorganizing. In addition, GO terms may comprise of multiple pathways, some of them divergent and some of them conserved. The various proposed classes of SCOMs capture this complexity, and indeed genes related to ribosome biogenesis appear in conserved SCOMs as well as within expanded SCOMs. In addition, processes related to response to starvation appear in separated and conserved SCOMs, as well as divergent SCOMs. This may relate to the specific properties and regulatory mechanisms of each pathway/gene.

Our analyses support the conjecture that organization and function/gene expression are related, but determining the mechanisms and causality of this relation is a more difficult challenge, and remains an open question. One direction in which this relation can be maintained, is by selection. There are various forms of gene rearrangement that may occur (duplication, transposition/retroposition, translocation, etc.). If such a rearrangement event may improve the fitness of the organism, e.g. by placing two functionally related genes in proximity/distance and improving/worsening the regulation over their co-expression, selection may act to prefer/purify this genomic organization (Figure 5F). It is also possible that closer genes undergo selection to have similar expression pattern/functionality. Moreover, recently, sequence mutations have been shown to directly affect the 3D organization, for example at topological associated domains (TADs) boundaries (16,82). Possibly, additional types of sites shape the 3D organization of genes and may be under selection.

However, it should be noted that non-random gene organization does not necessarily imply the activity of selection; it may be simply related to biophysical nature of gene regulation and its relation to genomic proximity. For example, opening chromatin to allow expression from one gene might incidentally allow leaky expression in its neighboring genes. However, based on the various types of analysis performed here, we believe that at least part of the detected signal is related to selection. It has been suggested that co-evolution between linearly neighboring genes may drive their expression level in the same direction once one of the genes changes its activity, thus promoting the formation of co-expressed domains/modules (83). This principle could also apply to neighboring genes in 3D.

Our approach can be employed in the study of other organisms for which chromosome conformation data exists, such as higher eukaryotes. The runtime of SCOM detection for any of the proposed classes in yeast is roughly 30 min on a modern PC. We expect that this performance can be further improved in the future. However, given the complexity of the statistical analysis and interpretation of the SCOMs above, we defer the expansion to other organisms to future studies.

The methods proposed here can be extended to large-scale multi-organismal analysis of the evolution of gene organization in various ways. For example, using methods such as maximum parsimony we can infer distances between families at internal nodes of the tree; we can, for example, place an edge between two families if their distance becomes gradually closer down the tree in a certain path from the node to a leaf, or in a large enough fraction of paths. We can also divide the organisms to major groups (e.g. bacteria versus eukaryotes) and add an edge if the distance between two families is small in most of the organisms in one group but is large in most of the organisms in the second group.

Finally, the proposed algorithms in this paper can be utilized for various purposes, such as studying differential genomic organization between tissues. It has been shown that genomic organization plays a crucial role in the development of cancer (17,23). We suggest that our methods can be used to find functional hotspots in the organization of cancerous cells. In the future, many additional module definitions can be formulated and solved in a similar manner to the SCOMs proposed here. For example, cell-to-cell variation can be studied using single-cell Hi-C, and networks representing the observed variance in gene distances. Additional information can also be incorporated into the orthologous networks as edges, based on annotations and/or experiments.

AVAILABILITY

All conserved and divergent SCOMs were uploaded to the NDEx (84) website, where they can be browsed and studied interactively. Links to NDEx networks and scripts for SCOM detection are available from: http://www.cs.tau.ac.il/∼tamirtul/SCOMs/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

A.D. is grateful to the Azrieli Foundation for the award of an Azrieli Fellowship; Edmond J. Safra Center for Bioinformatics at Tel Aviv University (in part). Funding for open access charge: TAU.

Conflict of interest statement. None declared.