Abstract
Membrane proteins control the traffic across cell membranes and thereby play an essential role in cell function from transport of various solutes to immune response via molecular recognition. Because it is very difficult to determine the structures of membrane proteins experimentally, computational methods have been increasingly used to study their structure and function. Here we focus on two classes of membrane proteins—ion channels and transporters—which are responsible for the generation of action potentials in nerves, muscles, and other excitable cells. We describe how computational methods have been used to construct models for these proteins and to study the transport mechanism. The main computational tool is the molecular dynamics (MD) simulation, which can be used for everything from refinement of protein structures to free energy calculations of transport processes. We illustrate with specific examples from gramicidin and potassium channels and aspartate transporters how the function of these membrane proteins can be investigated using MD simulations.
Keywords: Molecular dynamics, Ion channels, Transporters, Free energy calculations
Introduction
Cell membranes are impenetrable to most solutes in the plasma. This is especially so for ions and charged molecules, which face a large Born energy barrier to go from the high dielectric water environment (ε = 80) to the low dielectric lipid environment (ε = 2). Transport of ions and biomolecules across the membrane is accomplished by specific proteins embedded in the membrane, which are called ion channels and transporters (or pumps), respectively. Ion channels provide water-filled pathways for passive diffusion of ions down their electrochemical gradient, whereas transporters use either ATP or the energy stored in the membrane potential to move ions or substrates against their electrochemical gradient. Passive diffusion is a much simpler process than active pumping of ions or biomolecules. Therefore both the structure of transporter proteins and their function are much more complex compared to the ion channels. This is reflected in the progress made in the respective fields; while we know a great deal about the structure of channels and how they operate, our knowledge of transporters is still far from being complete. This review will reflect the current state of progress and focus more on ion channels than transporters.
Ion channels
Besides providing water-filled holes in the membrane for passive diffusion of ions, channels have two other properties that make their structure more complex and also make them more interesting to study, namely, ion selectivity and gating. Ion selectivity refers to the ability of each channel to conduct mainly one species of ion. The extracellular Na+ concentration is about 10-fold higher than the intracellular Na+ concentration, and the intracellular K+ concentration is about 30-fold higher than the extracellular K+ concentration. Further, the concentrations of both Na+ and K+ are much higher than those of Ca2+. These concentration differences are responsible for the membrane potential and must be maintained for normal cell function. Furthermore, generation of action potentials and muscle contraction rely on the ability of ion channels to discriminate among different ions by conducting only a selected type of ion (Hille 2001).
The second property is gating, which controls opening and closing of a channel. Ion channels can be gated by changes in the potential difference across the membrane (voltage-gated channels), by binding of small chemical transmitter molecules to the channel (ligand-gated channels), or by mechanical stimulus (stretch-activated channels) (Hille 2001). In voltage-gated channels, changes in the membrane potential cause charges to move across the voltage sensor of the channel, which triggers its opening. In ligand-gated channels, binding of a ligand provides the necessary free energy to drive the channel from the closed conformation to the open one. Finally stretch-activated channels respond to changes in surface tension in the membrane.
Two milestones in the ion channel field are the invention of the patch-clamp method by Neher and Sakmann (1976) and the first determination of the crystal structure of a biological ion channel by MacKinnon’s group (Doyle et al. 1998). The patch-clamp method enabled noise-free measurement of tiny (~ pico ampere) single-channel currents. Since the 1980s conductance properties of numerous ion channels have been determined. These include the current-voltage (I–V) and conductance-concentration (G–c) curves, and the permeability ratios of various ionic species (Hille 2001). For symmetric baths, the I–V curves mostly follow Ohm’s law (i.e. linear) in the physiological range of membrane potentials, namely, –100 < V < 50 mV. The G–c curves exhibit saturation behavior, which is described by the Michaelis-Menten relationship, G = G max /(1 + c s /c), where G max is the maximum conductance of the channel and c s is the saturation concentration at half-maximum. This simply follows from the fact that ion channels are too narrow and can conduct only one ion at a time—just like an enzyme that can process only one substrate at a time.
Membrane proteins are embedded in a low dielectric lipid environment, which makes them notoriously difficult to crystallize. The first crystal structure determination of the bacterial KcsA potassium channel (Doyle et al. 1998) was therefore a real breakthrough and earned MacKinnon the 2003 Nobel Prize. Since then the structure of a number of other channels have been determined, for example, the mechanosensitive (Chang et al. 1998), chloride (Dutzler et al. 2002), voltage-gated potassium (Long et al. 2005), and sodium (Payandeh et al. 2011) channels. Despite these developments, crystallization of membrane proteins remains a very challenging task, and structures of many important channels, such as calcium and nicotinic acetylcholine receptor, are yet to be determined.
In the absence of a structure, it is almost impossible to make accurate models of ion channels and predict their properties. Thus until 1998 little work was done on modelling of biological ion channels. One exception is the antibacterial peptide gramicidin, which forms a narrow pore in membranes, and whose structure was determined from NMR quite early (Urry 1971). Thus gramicidin has been the focus of early efforts on modelling of ion channels (Roux and Karplus 1994). Since the structure of a potassium channel became available, there has been an intense effort to study the structure-function relations in this channel using a variety of approaches ranging from the particle-based molecular dynamics (MD) and Brownian dynamics (BD) simulations to the continuum Poisson-Nernst-Planck equations (for reviews, see Kuyucak et al. 2001; Tieleman et al. 2001; Roux 2005). Because the continuum theories were shown to be invalid in narrow pores (Moy et al. 2000; Corry et al. 2000), BD (Chung et al. 1999, 2002a, b) and MD simulations (Allen et al. 1999, 2000; Aqvist and Luzhkov 2000; Berneche and Roux 2001, 2002; Shrivastava and Sansom 2000; Shrivastava et al. 2002) have been the two main approaches used in studies of potassium channels.
In MD, all the atoms in the system—ions, water molecules, protein and lipid atoms—are simulated by following their trajectories according to Newton’s equation of motion. In BD only the trajectories of the ions in the system are followed via the Langevin equation, and the rest of the atoms in the system are treated as continua. The effects of water molecules on the ions are taken into account via the friction and random forces. Here it is worthwhile to emphasize the complementary nature of the MD and BD approaches. While MD simulations provide a fundamental approach for studying ion permeation in channels, they are too slow to determine the conductance of a channel, which is the main observable. This can be readily achieved using BD simulations as they are several orders of magnitude faster than MD. However, the accuracy of the BD simulations may be compromised if one uses continuum electrostatics to calculate the forces acting on ions because it is known to break down in narrow pores (Edwards et al. 2002). A practical resolution of this problem is offered by combining the two methods, that is, one calculates the average forces acting on ions in the channel from MD simulations and uses these microscopically determined forces in BD simulations (Berneche and Roux 2002).
Transporters
The transporter field has been developing along similar lines to ion channels but more slowly due to the complexities mentioned above. Transporters are classified according to the source of the energy they use: primary active transporters use the energy released from the ATP hydrolysis reaction, while secondary active transporters exploit the energy stored in the membrane potential by coupling the uphill movement of a substrate to the favorable movement of ions. The ATP-binding cassette (ABC) transporters and the sodium-potassium pump are primary examples of the first class. The ABC transporters pump amino acids, peptides, proteins, metal ions, lipids, hydrophobic compounds, and drugs across the cell membrane (Davidson and Chen 2004). They have gained notoriety as the cause of multi-drug resistance to chemotherapy treatments—before anticancer drugs could have an effect on cancerous cells, they were pumped out by the ABC transporters (Gottesman et al. 2002). Several transporter structures from bacteria have been determined in recent years, for example, the vitamin B12 importer BtuCD from Escherichia coli (Locher et al. 2002), the metal chelate type importer HI1470 from Haemophilus influenza (Pinkett et al. 2007), and the exporter Sav1866 from Staphylococcus aureus (Dawson and Locher 2006). Of particular importance for multidrug resistance studies is the determination of the structure of P-glycoprotein (Aller et al. 2009).
The sodium-potassium pump is responsible for maintaining the membrane potential, which is essential for the generation of action potential. It uses the energy from one ATP molecule to export three Na+ ions out and import two K+ ions into the cell, making it an extremely efficient machine. Its crystal structure has also been determined recently (Preben Morth et al. 2007), which will eventually enable a mechanistic understanding of how this pump works.
Among the secondary active transporters, glutamate transporters play an important role in normal functioning of neurons. Glutamate is the major excitatory neurotransmitter in the central nervous system, and its extracellular concentration needs to be tightly controlled to prevent excessive stimulation of neurons, otherwise it may lead to cell death (Zerangue and Kavanaugh 1996). This is achieved by glutamate transporters—membrane proteins that continuously remove extracellular glutamate using the electrochemical gradient of Na+ and K+ ions. Crystal structure of an aspartate transporter GltPh from Pyrococcus horikoshii from Archaea has been determined both in the outward-open (Yernool et al. 2004; Boudker et al. 2007) and inward-open states (Reyes et al. 2009). The amino acid sequence of GltPh is 36 % identical to the human glutamate transporters, and most of the residues that have been identified as crucial for transporter function are conserved. Thus, GltPh provides a good working model for studying the structure and function of the human glutamate transporters.
Because the transport mechanism in transporters is much more complicated than in ion channels, computational methods are expected to play an even more important role in studies of transporter proteins. As in the case of channels, MD cannot provide a complete picture and one has to use coarse-grained models to study the slow degrees of freedom, such as switching from the extracellular open configuration to the intracellular one. Also quantum mechanical methods are required to describe the ATP hydrolysis reaction. After the determination of the crystal structures of ABC transporters, several groups started working on MD simulations of ABC transporters (for a review, see Oloo et al. 2006). In initial MD simulations of the vitamin B12 ABC transporter BtuCD, the effect of the binding of ATP and the periplasmic binding protein BtuF were investigated (Ivetac et al. 2007). Coarse-grained methods have been employed to study the conformational changes associated with ATP binding and hydrolysis (Liao and Beratan 2004; Sonne et al. 2007). In both cases the elastic network model was applied to BtuCD, and the results indicated that the two parts of the BtuCD dimer could act as semi-rigid lever arms, moving in opposite directions to open the cytoplasmic gate. Long MD simulations have also been used to study the opening of the nucleotide binding domains (Wen and Tajkhorshid 2008). So far there has not been much progress on computational description of the ATP hydrolysis reaction in ABC transporters.
Modelling of secondary active transporters has started since the appearance of the structure of GltPh (for a review, see Forrest et al. 2011). Several MD simulations of the outward-open structure of GltPh have been carried out to investigate the binding sites for Na+ ions and substrate and to confirm the opening of the extracellular gate (HP2) in the absence of ions and substrate (Shrivastava et al. 2008; Huang and Tajkhorshid 2008, 2010). More recently free energy calculations and mutagenesis experiments have been performed to identify the location of the binding site for the third Na+ ion and the binding order of ions and aspartate (Heinzelmann et al. 2011; Bastug et al. 2012).
Molecular dynamics simulations
Atomistic simulation of a typical membrane protein in its native environment of water and lipid molecules requires consideration of on the order of 105 atoms. Thanks to the phenomenal increase in computer power in the last few decades, one can now perform such calculations on a standard workstation. Use of clusters of computers has also cut down the computing time, bringing microsecond MD simulations of proteins within reach. Availability of several user-friendly packages specifically designed for simulation of biomolecular systems has also been instrumental in widespread use of the MD method in the biochemistry and molecular biology communities. Here we give a brief introduction to the basic formalism for MD simulations and refer the reader to monographs for a detailed exposition (Allen and Tildesley 1987; Frenkel and Smit 1996; Leach 2001).
In MD simulations, one follows the trajectories of N particles according to Newton’s equation of motion:
 |
1 |
where U(r 1,…, r N) is the potential energy function of N particles consisting of the bonded and non-bonded interactions. The bonded interactions describe the interactions of the covalently bound atoms in proteins and lipid molecules:
Here the first two harmonic terms represent the bond stretching and bending. Because covalent bonds are very strong, both spring parameters k are very stiff. The last term represents the torsion interaction among four neighboring atoms. It is relatively weaker (~ 1 kT) and is responsible for the formation of helical and other secondary structures in proteins.
The non-bonded interactions can be decomposed into four pieces:
Coulomb energy between two atoms with charges q i and q j and separated by a distance r ij has a two-body form:
| 2 |
-
2.
Polarization interaction between atoms depends on the induced dipole moment of the atoms, which is determined by the total electric field acting on each atom. Because the induced dipoles affect the electric field, it cannot be reduced to a two-body form.
-
3.
Dispersion (van der Waals) potential results from quantum dipole fluctuations. It is weakly attractive and has a 1/r 6 dependence.
-
4.
Short-range repulsion arises from the Pauli exclusion that prevents overlap of electron clouds. It has an exponential dependence on the distance between two atoms.
For convenience the last two interactions are combined in the form of a 12-6 Lennard-Jones (LJ) potential:
| 3 |
Here ε corresponds to the depth of the potential at the minimum (r = 21/6σ), and the potential vanishes at r = σ. These two parameters are determined for identical atoms. For different atoms, one uses the combination rules:
| 4 |
Implementation of the Coulomb and LJ terms is straightforward, but calculation of the induced polarization requires iteration of the polarization equations, which increases computational cost by several-fold. This was an important consideration in the early applications of MD, and as a result, the polarization interaction has not been included explicitly in the current force fields. Of course, it cannot be ignored completely, so the solution adapted was to boost the partial charges on the atoms so that the effect of polarization was taken into account in an average way. This mean field approximation appears to have worked reasonably well for globular proteins where water provides a uniform dielectric environment. However, one should be aware of potential problems in channels, cavities, and interfaces where polarization effects are expected to be non-uniform. This issue is further discussed below in MD simulations of the gramicidin A channel.
Integration algorithms
Given the position and velocities of N particles at time t, a straightforward integration of Newton’s equation of motion yields the following at t + Δt:
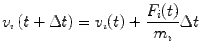 |
5 |
| 6 |
In practice, variations of these equations are implemented in MD codes. In the popular Verlet algorithm, one eliminates velocities by adding the time-reversed position at t − Δt:
| 7 |
to Eq. (6) giving
| 8 |
This is especially useful in situations where one is interested only in the positions of the atoms. If required, velocities can be calculated from
| 9 |
The Verlet algorithm has several drawbacks: (1) positions are obtained by adding a small quantity (order Δt 2) to large ones, which may lead to a loss of precision, (2) velocity at time t is available only at the next time step t + Δt, (3) it is not self starting, i.e., at t = 0, there is no position at t − Δt. These drawbacks are avoided in the leap-frog algorithm, where the positions and velocities are calculated at different times separated by Δt/2:
| 10 |
| 11 |
To start iteration of the equations, we need to specify the initial conditions:
The initial configuration of biomolecules can be taken from the Protein Data Bank (PDB) (if available).
In addition, membrane proteins need to be embedded in a lipid bilayer. VMD software (Humphrey et al. 1996) has a facility that will perform this step with minimal effort.
All the MD codes have facilities to hydrate a biomolecule, i.e., fill the void in the simulation box with water molecules at the correct density.
Finally ions can be added at random positions. Alternatively, VMD solves the Poisson-Boltzmann equation and places the ions where the potential energies are at minimum.
After energy minimization, these coordinates give the positions of atoms at t = 0. The initial velocities are sampled from a Maxwell-Boltzmann distribution:
| 12 |
In choosing a time step, one has to compromise between two conflicting demands: (1) in order to obtain statistically significant results and access biologically relevant time scales, one needs long simulation times, which requires a long time step, and (2) to avoid instabilities, conserve energy, etc., one needs to integrate the equations as accurately as possible, which requires using a short time step. For simulation of biomolecules, the recommended time step is around 1–2 fs.
Boundaries and ensembles
In macroscopic systems, the boundaries are far away from a system under consideration, hence their effect on the dynamics of biomolecules is negligible. In MD simulations, however, the system size is much smaller and one has to worry about the boundary effects. Using nothing (vacuum) is not realistic for bulk simulations because a vacuum creates an ordering of surface waters, which could influence the dynamics of a biomolecule separated by a few layers of water from the surface. One solution is to treat water beyond the simulation box implicitly using a continuum representation (reaction field). The most common solution is to use periodic boundary conditions. That is, the simulation box is replicated in all directions just like in a crystal. The cube and rectangular prism are the obvious choices for a box shape, though other shapes are also possible. Application of the periodic boundary conditions results in an infinite system which, in turn, raises the question of accurate calculation of the long-range Coulomb interactions. This problem has been resolved using Ewald’s sum methods, where the long-range part is separately evaluated in the reciprocal Fourier space (see the textbooks quoted above for further details).
MD simulations are typically performed in the NVE ensemble, where all three quantities (number of atoms, volume, and energy) are constant. Due to truncation errors, keeping the energy constant in long MD simulations can be problematic. To avoid this problem, the alternative NVT and NPT ensembles are employed. The temperature of the system is obtained from the average kinetic energy:
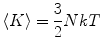 |
13 |
Thus an obvious way to keep the temperature constant at T 0 is to scale the velocities as:
| 14 |
Because the kinetic energy has considerable fluctuations, this is a rather crude method. A better method, which achieves the same result more smoothly, is the Berendsen thermostat, where the atoms are weakly coupled to an external heat bath with the desired temperature T 0:
| 15 |
If T(t) > T 0 , the coefficient of the coupling term is negative, which invokes a viscous force slowing the velocity, and vice-versa for T(t) < T 0 . Similarly in the NPT ensemble, the pressure can be kept constant by simply scaling the volume. Again this is very crude, and a better method is to weakly couple the pressure difference to atoms using a similar force as above (Langevin piston), which will maintain the pressure at the desired value of ~1 atm.
Several codes are available for MD simulations. The most common ones are CHARMM (MacKerell et al. 1998), AMBER (Pearlman et al. 1995), GROMACS (Lindahl et al. 2001), and NAMD (Phillips et al. 2005). The first three have their own force fields, while NAMD can be used with any force field. CHARMM and AMBER force fields were developed for simulations of proteins and nucleic acids and are very similar. GROMACS was initially developed for lipid simulations and was less successful for proteins, although it has been improved in later versions.
Analysis of trajectory data
In a typical MD simulation, one first equilibrates the system and then collects trajectory data to be analyzed later. The trajectory data consist of the positions and velocities of all the atoms in the system. Some of the important quantities used in the analysis are described below.
Root mean square deviation (RMSD)
For an N-atom system, the variance and RMSD at time t are defined as:
| 16 |
Where r i(0) are the reference coordinates. Usually they are taken from the first frame in an MD simulation, though they can also be taken from the PDB or a target structure. Because side chains in proteins are different, it is common to use a restricted set of atoms such as backbone or Cα. RMSD is very useful in monitoring the approach to equilibrium, typically signaled by the appearance of a broad shoulder. It is a good practice to keep monitoring RMSD during production runs to ensure that the system stays near equilibrium.
Distribution functions
Pair distribution function g ij(r) gives the probability of finding a pair of atoms (i, j) at a distance r. It is obtained by sampling the distance r ij in MD simulations and placing each distance in an appropriate bin, [r, r + Δr]. Pair distribution functions are used in characterizing correlations between pairs of atoms, e.g., hydrogen bonds and coordination of cations by carbonyl oxygens. The peak gives the average pair distance, and the width is correlated with the strength of the interaction.
Conformational analysis
In proteins, the bond lengths and bond angles are more or less fixed. Thus we are mainly interested in conformations of the torsional angles. As the shape of a protein is determined by the backbone atoms, the torsional angles, ϕ (N − Cα) and ψ (C − Cα), are of particular interest. These are conveniently analyzed using the Ramachandran plots. Conformational changes in a protein during MD simulations can be most easily revealed by plotting these torsional angles as a function of time.
Free energy calculations
Free energy is the most important quantity that characterizes a dynamic process. Calculation of the absolute free energies is difficult in MD simulations. However, free energy differences can be estimated more easily, and several methods have been developed for this purpose. The starting point for most approaches is Zwanzig’s perturbation formula for the free energy difference between two states A and B:
| 17 |
If the two states are not similar enough, there will be a large hysteresis effect, and the forward and backward results will not be equal.
Alchemical transformation methods
To obtain accurate results with the perturbation formula, the energy difference between the states should be less than 2 kT (Beveridge and DiCapua 1989), which is not satisfied for most biomolecular processes. To deal with this problem, one introduces a hybrid Hamiltonian:
| 18 |
and performs the transformation from A to B gradually by changing the parameter λ from 0 to 1 in small steps. That is, one divides [0,1] into n subintervals with {λ i , i = 0, n}, and for each λ i value, calculates the free energy difference from the ensemble average:
| 19 |
The total free energy change is then obtained by summing the contributions from each subinterval:
 |
20 |
The number of subintervals is chosen so that the free energy change at each step does not exceed 2 kT, otherwise the method may lose its validity. Another method to obtain the free energy difference is thermodynamic integration, where one integrates the derivative of the hybrid Hamiltonian:
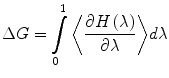 |
21 |
This integral is evaluated most efficiently using a Gaussian quadrature.
Absolute free energies from umbrella sampling
In this method one samples the densities along a reaction coordinate and determines the potential of mean force (PMF) from the Boltzmann equation.
| 22 |
Here z 0 is a reference point in bulk where W vanishes. In general, a particle cannot be adequately sampled at high-energy points. To counter that, one introduces harmonic potentials, which restrain the particle at desired points and then unbias its effect (Torrie and Valleau 1977). For convenience, one introduces an umbrella potential at regular intervals (e.g., 0.5 Å) along the reaction coordinate, which is the channel axis. The PMFs obtained in each interval are unbiased and combined using the weighted histogram analysis method (Kumar et al. 1992).
MD simulations of ion channels
Gramicidin A channel
Gramicidin A (gA) is the simplest known ion channel and its structure has been known since the early 1970s. Therefore the first MD simulations of ion channels were performed in gA (Roux and Karplus 1994). The structure of gA is unique and very different from the biological ion channels. For example, the channel radius is about 2 Å, which forces ions and water into a single file configuration (Fig. 1). Despite this, the channel conducts monovalent cations at near diffusion rates. The ion-water configurations and hence the interactions are very different in gA compared to bulk water. This means that gA may not be a good template for biological ion channels. But because of its simplicity, it still offers an ideal test ground for checking the accuracy of force fields and free energy methods.
Fig. 1.
Gramicidin A dimer (left) embedded in a lipid bilayer and hydrated with water and KCl ions (right). The simplified representation of the simulation system shows only the lipid head groups (purple) and the gA backbone atoms (green)
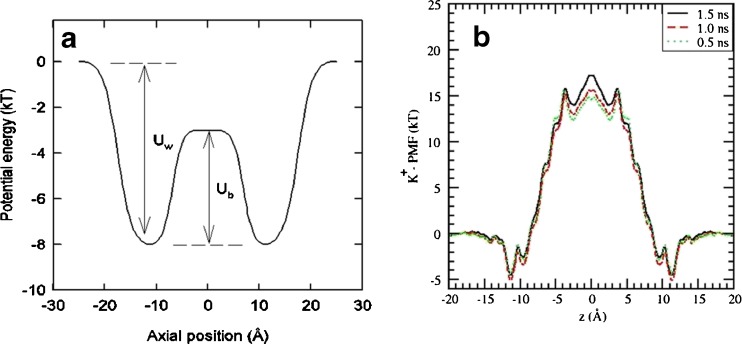
Many MD simulations of gA have been performed in recent years for such purposes. Here we discuss testing of the force fields, which has far reaching ramifications because of the missing polarization interaction in current force fields. In Fig. 2, the potential energy profile of a K+ ion obtained from the conductance data (Edwards et al. 2002) is compared with the PMF obtained from MD simulations (Bastug and Kuyucak 2007). While there is a reasonable agreement for the well depth, the central energy barrier predicted by MD is too large to be compatible with the conductance data, which requires Ub < Uw. It has been conjectured that the single file configuration of ion and waters in gA is more favorable for the polarization interaction compared to the bulk geometry, so that its inclusion in the force fields will resolve the problem with the large energy barrier (Allen et al. 2003; Bastug and Kuyucak 2006). Recent ab initio MD simulations show that water is more polarized in gA compared to the hydration shell of a K+ ion in bulk (Bucher and Kuyucak 2008, 2009) lending further support for this conjecture. For definitive proof, PMF calculations with polarizable force fields need to be performed, which are still under development. Investigation of the effect of polarization in ion channels and of membrane proteins in general is expected to be a major research area in this decade (Lopes et al. 2009).
Fig. 2.
Potential energy profile of a K+ ion along the central axis of gA obtained from BD simulations by inverting the experimental data (left), which yields Uw = 8 kT for the well depth at the channel entrance, and Ub = 5 kT for the barrier height at the center. For comparison, the PMF of a K+ ion in gA obtained from MD simulations (right) gives Uw = 5 kT, Ub = 22 kT
Potassium channels
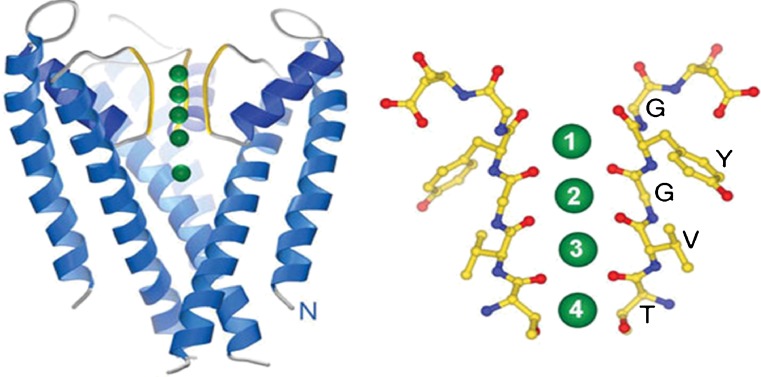
The crystal structure of the bacterial KcsA potassium channel (Fig. 3) revealed the basic topology of this class of channels and how they selectively conduct K+ ions. Each binding site in the filter is coordinated by eight carbonyl oxygens, which mimic the hydration shell of a K+ ion in water. Thus a K+ ion can enter the filter with almost no energy penalty. Because the positions of the carbonyl oxygens are optimized for solvating a K+ ion and Na+ ions are smaller, they are not as well solvated in the filter and rejected. While this selectivity mechanism is obtained for a bacterial channel, the filter sequence TVGYG is conserved in all potassium channels, thus the same mechanism is expected to apply universally. Diversity in the conductance range of potassium channels (almost two orders of magnitude) is, instead, explained by variations in the intracellular radius (Chung et al. 2002b).
Fig. 3.
Crystal structure of the KcsA potassium channel (Doyle et al. 1998) showing the selectivity filter (yellow) and binding sites for K+ ions (green). It has a tetrameric structure but only two of the monomers are shown for clarity. A magnified view of the filter depicting the carbonyl oxygens (red) that form the four binding sites is shown on the right. A fifth binding site (S0) is formed just above the S1 site
Many groups have been involved in MD simulations of the potassium channels. The main challenges are quantitative description of the selectivity and permeation properties. The early calculations of the free energy of the K+/Na+ selectivity are summarized in the review articles (Kuyucak et al. 2001; Tieleman et al. 2001; Roux 2005). The latest free energy perturbation calculations have resulted in a K+/Na+ selectivity free energy of 8.4 kcal/mol for KcsA and 5.2 kcal/mol for the mammalian Shaker Kv1.2 channels (Bastug and Kuyucak 2009). Both results are consistent with the experimental K+/Na+ permeability ratios. Here we stress that use of a correction term for the dihedral energies called CMAP (MacKerell et al. 2004) is necessary for a proper description of the selectivity filter especially in the Shaker Kv1.2 channel. Without this term, the carbonyl groups in the filter are observed to flip away from the channel axis, and the channel loses its selectivity property.
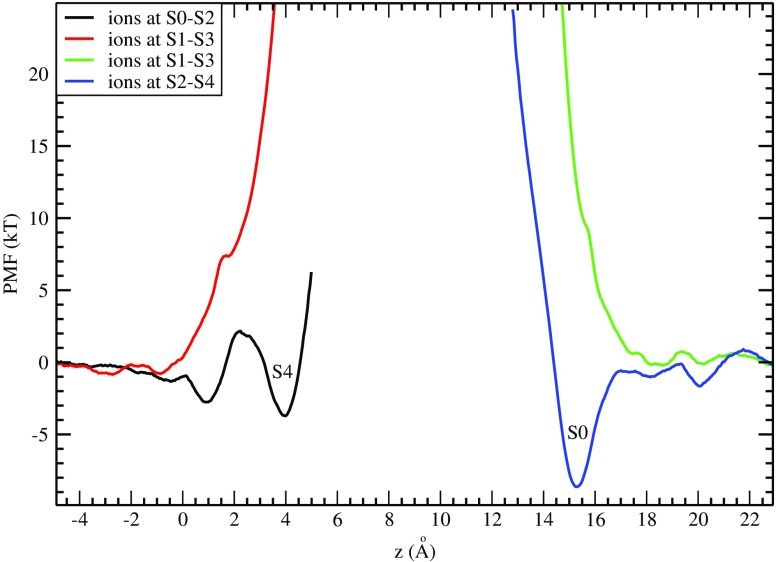
A direct study of conductance of K+ ions in potassium channels via MD requires millisecond simulations, and hence it is very difficult to achieve with the current computer clusters. Extension of simulation times by thousand-fold in recently built special purpose clusters such as Anton (Dror et al. 2012) has enabled study of ion permeation and voltage-gating properties via MD (Jensen et al. 2010, 2012), but these clusters are not generally available. Nevertheless one can get a good idea about the permeation properties of potassium channels from the PMF of K+ ions (Bastug and Kuyucak 2011). The selectivity filter is permanently occupied by two K+ ions, residing in either S1-S3 or S2-S4 binding sites with a water molecule between them. A permeation event is triggered when a K+ ion moves from the cavity to the filter. MD simulations show that three K+ ions can occupy the filter at S0-S2-S4 sites in a semi-stable configuration. But it is not clear whether the third K+ ion can also bind to S4 forming a three ion configuration at S1-S3-S4. This question is addressed for the KcsA channel in Fig. 4, which shows the PMF of the third K+ ion while the other two are either in S1-S3 (red curve) or S0-S2 (black curve). No binding pocket is found at the S4 site in the former case, indicating that simultaneous occupation of the S1-S3-S4 sites is not feasible. Similar results have been obtained for the Shaker Kv1.2 channel (Bastug and Kuyucak 2011). For inward permeation, a K+ ion from bulk needs to bind to the S0 site. The PMF in Fig. 4 (blue curve) exhibits a binding pocket at S0 when the resident K+ ions are at S2-S4, indicating that this is readily feasible. However, this binding pocket disappears when the S1-S3 sites are occupied (green curve). Thus in both inward and outward permeation events, the main intermediate state is three K+ ions occupying the S0-S2-S4 sites separated by two water molecules at S1 and S3. This picture is consistent with the observation that one water molecule is cotransported with each ion and is also confirmed by direct MD simulations of permeation of K+ ions (Jensen et al. 2010).
Fig. 4.
PMF of a K+ ion in the KcsA channel showing its binding to the filter from the intracellular (left) and extracellular (right) sides. The inset shows the positions of the two other K+ ions resident in the filter
MD simulations of transporters
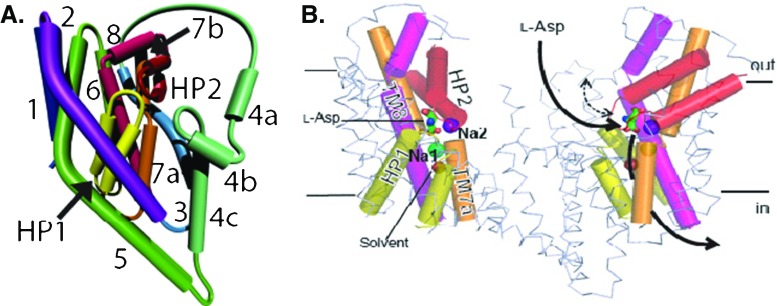
Modelling of transporters will require a variety of computational methods from ab initio to coarse grain, but classical MD will play a central role in this endeavor. Here we discuss application of MD simulations to the aspartate transporter protein GltPh, whose structure has been determined recently (Yernool et al. 2004; Boudker et al. 2007). This protein is a trimer, and each monomer contains eight transmembrane domains (TM1–8) and two hairpin loops termed HP1 and HP2 (Fig. 5). The binding pocket is formed by the residues from HP1, HP2, TM7, and TM8. GltPh transports three Na+ ions with each substrate, but only two of the ion binding sites were observed in the crystal structure (Fig. 5). Thus identification of the third Na+ binding site was an important issue in initial MD simulations of GltPh. Several sites have been proposed for this purpose, and the site formed by the residues, N310, D312 on TM7 and Y89, T92, S93 on TM8 has been confirmed in mutagenesis experiments (Bastug et al. 2012).
Fig. 5.
The topology of a single monomer of GltPh (left). Two monomers of GltPh are shown in the membrane (right). TM1–6 are in ribbon representation, TM7, 8, and HP1, HP2 are shown as cylinders, and bound aspartate is shown in stick representation. HP2 serves as an extracellular gate and controls access of Asp to its binding site. Na+ ion #1 is below the binding site, while Na+ ion #2 is above it and serves as a lock on this gate
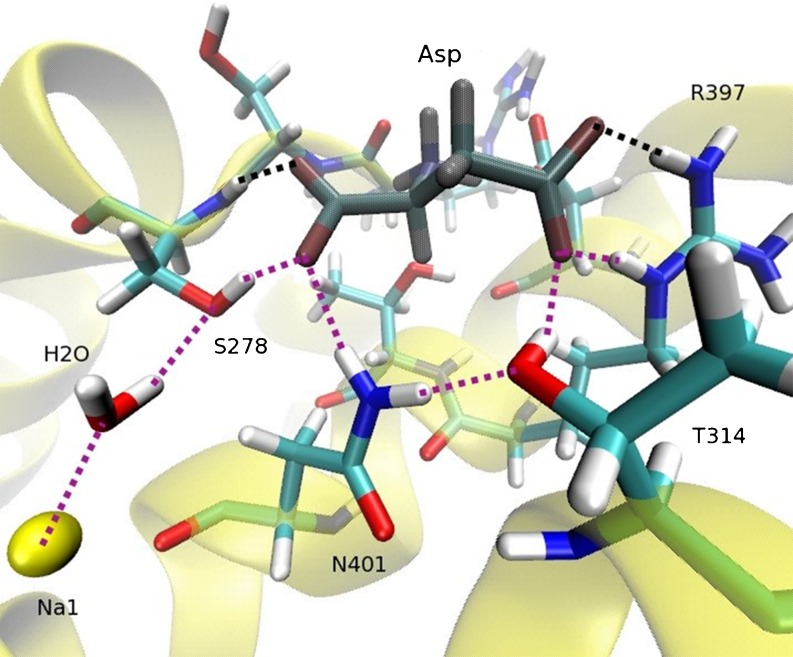
Besides finding and confirming the ion and Asp binding sites in GltPh, MD simulations have also been used to determine their binding free energies and thus their binding order (Heinzelmann et al. 2011). According to the free energy calculations, Na3 binds first with a free energy of −19 kcal/mol followed by Na1 (−7 kcal/mol) and Asp (−4 kcal/mol). The HP2 gate closes after Asp binds, and finally binding of Na2 between TM7 and HP2 (−3 kcal/mol) locks this gate. Unlike leucine transporters, there is no direct coupling between the ions and substrate in GltPh. Nevertheless MD simulations reveal that Asp is linked to Na1 via a hydrogen-bond network, and presence of Na1 is essential for binding of Asp (Fig. 6). When Na1 is removed from its binding site, this triggers breakdown of the hydrogen-bond network depicted by dotted lines in Fig. 6. The broken bonds in Asp are replaced by water molecules, and Asp is released from the binding site within a few nanoseconds. Similar MD simulations have been performed for the inward-open structure of GltPh (Reyes et al. 2009) and reveal a similar mechanism for unbinding of ions and Asp (Heinzelmann et al. 2011 ).
Fig. 6.
Binding site of Asp (dark-shaded) in the open state of GltPh. The hydrogen bonds are denoted by dotted lines, with the purple ones showing the chain of hydrogen bonds that stabilizes Asp in the binding site in the presence of Na1 (yellow). This structure remains stable throughout the simulations performed in the open state
Concluding remarks
Here we have given a brief description of the MD simulations and discussed a few of their applications to ion channels and transporters. More comprehensive reviews of MD simulations of membrane proteins can be found in Wang et al. (2010), Stansfeld and Sansom (2011), and Dror et al. 2012. As the appreciation of the MD simulations increases in the molecular biology/biochemistry communities, it is expected that applications of MD simulations to biomolecules will keep growing at an exponential rate in the near future. It is important for the next generation of researchers to be familiar with these methods and use them to complement the laboratory work. Crystal structures of proteins provide important insights for understanding the structural basis of their function. However, structure alone is not enough to get a complete understanding of their functional mechanisms such as selectivity, permeation, and transport. To address these issues, one needs to use the crystal structure in MD simulations, which will enable detailed description of interactions of ions and substrates with the protein and also how the protein responds to accommodate these events. Furthermore, simulation studies make predictions that can be tested in new experiments. As is well known in other, more established fields, the feedback provided from theory to experiment and vice versa greatly speeds up the discovery process.
Despite the progress made in the last decade in the field of ion channels and transporters, there is still a great deal of work to be done. Structures of only a handful of channel and transporter proteins have been determined so far, and without structure our understanding of function remains poor. Finally, understanding the structure-function relations in proteins is the first step towards the ultimate goal of finding the molecular basis of diseases and designing novel drugs for their treatment. Here too simulation methods will be very useful. For example, how a specific mutation in a protein affects its function can be studied in molecular detail via MD simulations, and as well a compound can be designed that will bind to a dysfunctional protein with high affinity and modulate its behavior.
Acknowledgments
This work was supported by grants from the Australian Research Council and Turkish Scientific and Technical Research Council (TUBITAK). Calculations were performed using the HPC facilities at the National Computational Infrastructure (Canberra) and ULAKBIM (Ankara).
Abbreviations
- ABC
ATP binding cassette
- BD
Brownian dynamics
- gA
Gramicidin A
- MD
Molecular dynamics
- PMF
Potential of mean force
- RMSD
Root mean square deviation
Footnotes
Special issue: Computational Biophysics
References
- Allen MP, Tildesley DJ. Computer simulation of liquids. London: Oxford University Press; 1987. [Google Scholar]
- Allen TW, Kuyucak S, Chung SH. Molecular dynamics study of the KcsA potassium channel. Biophys J. 1999;77:2502–2516. doi: 10.1016/S0006-3495(99)77086-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen TW, Bliznyuk A, Rendell AP, Kuyucak S, Chung SH. The potassium channel: structure, selectivity and diffusion. J Chem Phys. 2000;112:8191–8204. doi: 10.1063/1.481420. [DOI] [Google Scholar]
- Allen TW, Bastug T, Kuyucak S, Chung SH. Gramicidin A as a test ground for molecular dynamics force fields. Biophys J. 2003;84:2159–2168. doi: 10.1016/S0006-3495(03)75022-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aller SG, Yu J, Ward A, Weng A, Chittaboina S, Zhuo R, Harrell PM, Trinh YT, Zhang Q, Urbatsch I, Chang J. Structure of P-glycoprotein reveals a molecular basis for poly-specific drug binding. Science. 2009;323:1718–1722. doi: 10.1126/science.1168750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aqvist J, Luzhkov V. Ion permeation mechanism of the potassium channel. Nature. 2000;404:881–884. doi: 10.1038/35009114. [DOI] [PubMed] [Google Scholar]
- Bastug T, Kuyucak S. Energetics of ion permeation, rejection, binding and block in gramicidin A from free energy simulations. Biophys J. 2006;90:3941–3950. doi: 10.1529/biophysj.105.074633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastug T, Kuyucak S. Free energy simulations of single and double ion occupancy in gramicidin A. J Chem Phys. 2007;126:105103. doi: 10.1063/1.2710267. [DOI] [PubMed] [Google Scholar]
- Bastug T, Kuyucak S. Importance of the peptide backbone description in modeling the selectivity filter in potassium channels. Biophys J. 2009;96:4006–4012. doi: 10.1016/j.bpj.2009.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastug T, Kuyucak S. Comparative study of the energetics of ion permeation in Kv1.2 and KcsA potassium channels. Biophys J. 2011;100:629–636. doi: 10.1016/j.bpj.2010.12.3718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastug T, Heinzelmann G, Kuyucak S, Salim M, Vandenberg RJ, Ryan RM. Position of the third Na+ site in the aspartate transporter GltPh from free energy simulations and site-directed mutagenesis experiments. PLOS One. 2012;7:e33058. doi: 10.1371/journal.pone.0033058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berneche S, Roux B. Energetics of ion conduction through the K+channel. Nature. 2001;414:73–77. doi: 10.1038/35102067. [DOI] [PubMed] [Google Scholar]
- Berneche S, Roux B. A microscopic view of ion conduction through the K+ channel. Proc Natl Acad Sci U S A. 2002;100:8644–8648. doi: 10.1073/pnas.1431750100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beveridge DL, DiCapua FM. Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu Rev Biophys Biophys Chem. 1989;18:431–492. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- Boudker O, Ryan RM, Yernool D, Shimamoto K, Gouaux E. Coupling substrate and ion binding to extracellular gate of a sodium-dependent aspartate transporter. Nature. 2007;445:387–393. doi: 10.1038/nature05455. [DOI] [PubMed] [Google Scholar]
- Bucher D, Kuyucak S. Polarization of water in the first hydration shell of K+ and Ca2+ ions. J Phys Chem B. 2008;112:10786–10790. doi: 10.1021/jp804694u. [DOI] [PubMed] [Google Scholar]
- Bucher D, Kuyucak S. Importance of water polarization for ion permeation in narrow pores. Chem Phys Lett. 2009;477:207–210. doi: 10.1016/j.cplett.2009.06.069. [DOI] [Google Scholar]
- Chang G, Spencer RH, Lee AT, Barclay MT, Rees DC. Structure of the MscL homolog from Mycobacterium tuberculosis: a gated mechanosensitive ion channel. Science. 1998;282:2220–2226. doi: 10.1126/science.282.5397.2220. [DOI] [PubMed] [Google Scholar]
- Chung SH, Allen TW, Hoyles M, Kuyucak S. Permeation of ions across the potassium channel: Brownian dynamics studies. Biophys J. 1999;77:2517–2533. doi: 10.1016/S0006-3495(99)77087-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung SH, Allen TW, Kuyucak S. Conducting-state properties of the KcsA potassium channel from molecular and Brownian dynamics simulations. Biophys J. 2002;82:628–645. doi: 10.1016/S0006-3495(02)75427-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung SH, Allen TW, Kuyucak S. Modeling diverse range of potassium channels with Brownian dynamics. Biophys J. 2002;83:263–277. doi: 10.1016/S0006-3495(02)75167-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corry B, Kuyucak S, Chung SH. Tests of continuum theories as models of ion channels: II. Poisson-Nernst-Planck theory versus Brownian dynamics. Biophys J. 2000;78:2364–2381. doi: 10.1016/S0006-3495(00)76781-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson AL, Chen J. ATP-binding cassette transporters in bacteria. Annu Rev Biochem. 2004;73:241–268. doi: 10.1146/annurev.biochem.73.011303.073626. [DOI] [PubMed] [Google Scholar]
- Dawson RJP, Locher KP. Structure of a bacterial multidrug ABC transporter. Nature. 2006;443:180–185. doi: 10.1038/nature05155. [DOI] [PubMed] [Google Scholar]
- Doyle DA, Cabral JM, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnon R. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- Dror RO, Dirks RM, Grossman JP, Xu H, Shaw DE. Biomolecular simulations: a computational microscope for molecular biology. Annu Rev Biophys. 2012;41:429–452. doi: 10.1146/annurev-biophys-042910-155245. [DOI] [PubMed] [Google Scholar]
- Dutzler R, Campbell EB, Cadene M, Chait BT, MacKinnon R. X-ray structure of a ClC chloride channel at 3.0 Å reveals the molecular basis of anion selectivity. Nature. 2002;415:287–294. doi: 10.1038/415287a. [DOI] [PubMed] [Google Scholar]
- Edwards S, Corry B, Kuyucak S, Chung SH. Continuum electrostatics fails to describe ion permeation in the gramicidin channel. Biophys J. 2002;83:1348–1360. doi: 10.1016/S0006-3495(02)73905-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forrest LR, Kramer R, Ziegler C. The structural basis of secondary active transport mechanisms. Biochim Biophys Acta. 2011;1807:167–188. doi: 10.1016/j.bbabio.2010.10.014. [DOI] [PubMed] [Google Scholar]
- Frenkel D, Smit B. Understanding molecular simulation: from algorithms to applications. San Diego: Academic Press; 1996. [Google Scholar]
- Gottesman MM, Fojo T, Bates SE. Multidrug resistance in cancer: role of ATP-dependent transporters. Nat Rev Cancer. 2002;2:48–58. doi: 10.1038/nrc706. [DOI] [PubMed] [Google Scholar]
- Heinzelmann G, Bastug T, Kuyucak S. Free energy simulations of ligand binding to the aspartate transporter GltPh. Biophys J. 2011;101:2380–2388. doi: 10.1016/j.bpj.2011.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. Ionic channels of excitable membranes. 3. Sunderland: Sinauer; 2001. [Google Scholar]
- Huang Z, Tajkhorshid E. Dynamics of the extracellular gate and ion-substrate coupling in the glutamate transporter. Biophys J. 2008;95:2292–2300. doi: 10.1529/biophysj.108.133421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z, Tajkhorshid E. Identification of the third Na+ site and the sequence of extracellular binding events in the glutamate transporter. Biophys J. 2010;99:1416–1425. doi: 10.1016/j.bpj.2010.06.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W, Dalke A, Schulten K. VMD—visual molecular dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Ivetac A, Campbell JD, Sansom MSP. Dynamics and function in a bacterial ABC transporter. Biochemistry. 2007;46:2767–2778. doi: 10.1021/bi0622571. [DOI] [PubMed] [Google Scholar]
- Jensen MO, Borhani DW, Lindroff-Larsen K, Maragakis P, Jogini V, Eastwood MP, Dror RO, Shaw DE. Principles of conduction and hydrophobic gating in K+ channels. Proc Natl Acad Sci USA. 2010;107:5833–5838. doi: 10.1073/pnas.0911691107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen MO, Jogini V, Borhani DW, Leffler AE, Dror RO, Shaw DE. Mechanism of voltage gating in potassium channels. Science. 2012;336:229–233. doi: 10.1126/science.1216533. [DOI] [PubMed] [Google Scholar]
- Kumar S, Bouzida D, Swensen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. J Comp Chem. 1992;13:1011–1021. doi: 10.1002/jcc.540130812. [DOI] [Google Scholar]
- Kuyucak S, Andersen OS, Chung SH. Models of permeation in ion channels. Rep Prog Phys. 2001;64:1427–1472. doi: 10.1088/0034-4885/64/11/202. [DOI] [Google Scholar]
- Leach AR. Molecular modelling, principles, applications. New York: Prentice Hall; 2001. [Google Scholar]
- Liao JL, Beratan DN. How does protein architecture facilitate the transduction of ATP chemical-bond energy into mechanical work? Biophys J. 2004;87:1369–1377. doi: 10.1529/biophysj.103.038653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J Mol Model. 2001;7:306–317. [Google Scholar]
- Locher KP, Lee AT, Rees DC. The E. coli BtuCD structure: a framework for ABC transporter architecture and mechanism. Science. 2002;296:1091–1098. doi: 10.1126/science.1071142. [DOI] [PubMed] [Google Scholar]
- Long SB, Campbell EB, MacKinnon R. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 2005;309:897–903. doi: 10.1126/science.1116269. [DOI] [PubMed] [Google Scholar]
- Lopes EM, Roux B, MacKerell AD., Jr Molecular modeling and dynamics studies with explicit inclusion of electronic polarizability: theory and applications. Theor Chem Acc. 2009;124:11–28. doi: 10.1007/s00214-009-0617-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck JD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- MacKerell AD, Feig M, Brooks CL. Extending the treatment of backbone energetics in protein force fields. J Comput Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- Moy G, Corry B, Kuyucak S, Chung SH. Tests of continuum theories as models of ion channels: I. Poisson-Boltzmann theory versus Brownian dynamics. Biophys J. 2000;78:2349–2363. doi: 10.1016/S0006-3495(00)76780-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher E, Sakmann B. Single-channel currents recorded from membrane of denervated frog muscle fibers. Nature. 1976;260:799–802. doi: 10.1038/260799a0. [DOI] [PubMed] [Google Scholar]
- Oloo EO, Kandt C, O’Mara ML, Tieleman DP. Computer simulations of ABC transporter components. Biochem Cell Biol. 2006;84:900–911. doi: 10.1139/o06-182. [DOI] [PubMed] [Google Scholar]
- Payandeh J, Scheuer T, Zheng N, Caterall WA. The crystal structure of a voltage-gated sodium channel. Nature. 2011;475:353–358. doi: 10.1038/nature10238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearlman DA, Case DA, Caldwell JW, Ross WS, Cheatham TE, DeBolt S, Ferguson D, Seibel G, Kollman AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics, and free energy calculations to simulate the structural and energetic properties of molecules. Comp Phys Commun. 1995;91:1–41. doi: 10.1016/0010-4655(95)00041-D. [DOI] [Google Scholar]
- Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinkett HW, Lee AT, Lum P, Locher KP, Rees DC. An inward-facing conformation of a putative metal-chelate type ABC transporter. Science. 2007;315:373–377. doi: 10.1126/science.1133488. [DOI] [PubMed] [Google Scholar]
- Preben Morth J, Pedersen BP, Toustrup-Jensen MS, Sorensen TL, Petersen J, Andersen JP, Vilsen B, Nissen P. Crystal structure of the sodium-potassium pump. Nature. 2007;450:1043–1049. doi: 10.1038/nature06419. [DOI] [PubMed] [Google Scholar]
- Reyes N, Ginter C, Boudker O. Transport mechanism of a bacterial homologue of glutamate transporters. Nature. 2009;462:880–885. doi: 10.1038/nature08616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux B. Ion conduction and selectivity in K+ channels. Annu Rev Biophys Biomol Struct. 2005;34:153–171. doi: 10.1146/annurev.biophys.34.040204.144655. [DOI] [PubMed] [Google Scholar]
- Roux B, Karplus M. Molecular dynamics simulations of the gramicidin channel. Annu Rev Biophys Biomol Struct. 1994;23:731–761. doi: 10.1146/annurev.bb.23.060194.003503. [DOI] [PubMed] [Google Scholar]
- Shrivastava IH, Sansom MSP. Simulation of ion permeation through a potassium channel: molecular dynamics of KcsA in a phospholipid bilayer. Biophys J. 2000;78:557–570. doi: 10.1016/S0006-3495(00)76616-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrivastava IH, Tieleman DP, Biggin PC, Sansom MSP. K+ versus Na+ ions in a K channel selectivity filter: a simulation study. Biophys J. 2002;82:633–645. doi: 10.1016/S0006-3495(02)75197-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrivastava IH, Jiang J, Amara SG, Bahar I. Time-resolved mechanism of extracellular gate opening and substrate binding in a glutamate transporter. J Biol Chem. 2008;283:28680–28690. doi: 10.1074/jbc.M800889200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonne J, Kandt C, Peters GH, Hansen FY, Jensen MO, Tieleman DP. Simulation of the coupling between nucleotide binding and transmembrane domains in the ABC transporter BtuCD. Biophys J. 2007;92:2727–2734. doi: 10.1529/biophysj.106.097972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stansfeld PJ, Sansom MSP. Molecular simulation approaches to membrane proteins. Structure. 2011;19:1562–1572. doi: 10.1016/j.str.2011.10.002. [DOI] [PubMed] [Google Scholar]
- Tieleman DP, Biggin PC, Smith GR, Sansom MSP. Simulation approaches to ion channel structure-function relationships. Q Rev Biophys. 2001;34:473–561. doi: 10.1017/S0033583501003729. [DOI] [PubMed] [Google Scholar]
- Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J Comp Phys. 1977;23:187–199. doi: 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
- Urry DW. The gramicidin A transmembrane channel: a proposed πLD helix. Proc Natl Acad Sci USA. 1971;68:672–676. doi: 10.1073/pnas.68.3.672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Shaikh SA, Tajkhorshid E. Exploring transmembrane diffusion pathways with molecular dynamics. Physiology. 2010;25:142–154. doi: 10.1152/physiol.00046.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen PC, Tajkhorshid E. Dimer opening of the nucleotide binding domains of ABC transporters after ATP hydrolysis. Biophys J. 2008;95:5100–5110. doi: 10.1529/biophysj.108.139444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yernool D, Boudker O, Jin Y, Gouaux E. Structure of a glutamate transporter homologue from Pyrococcus horikoshii. Nature. 2004;431:811–818. doi: 10.1038/nature03018. [DOI] [PubMed] [Google Scholar]
- Zerangue N, Kavanaugh MP. Flux coupling in a neuronal glutamate transporter. Nature. 1996;383:634–637. doi: 10.1038/383634a0. [DOI] [PubMed] [Google Scholar]