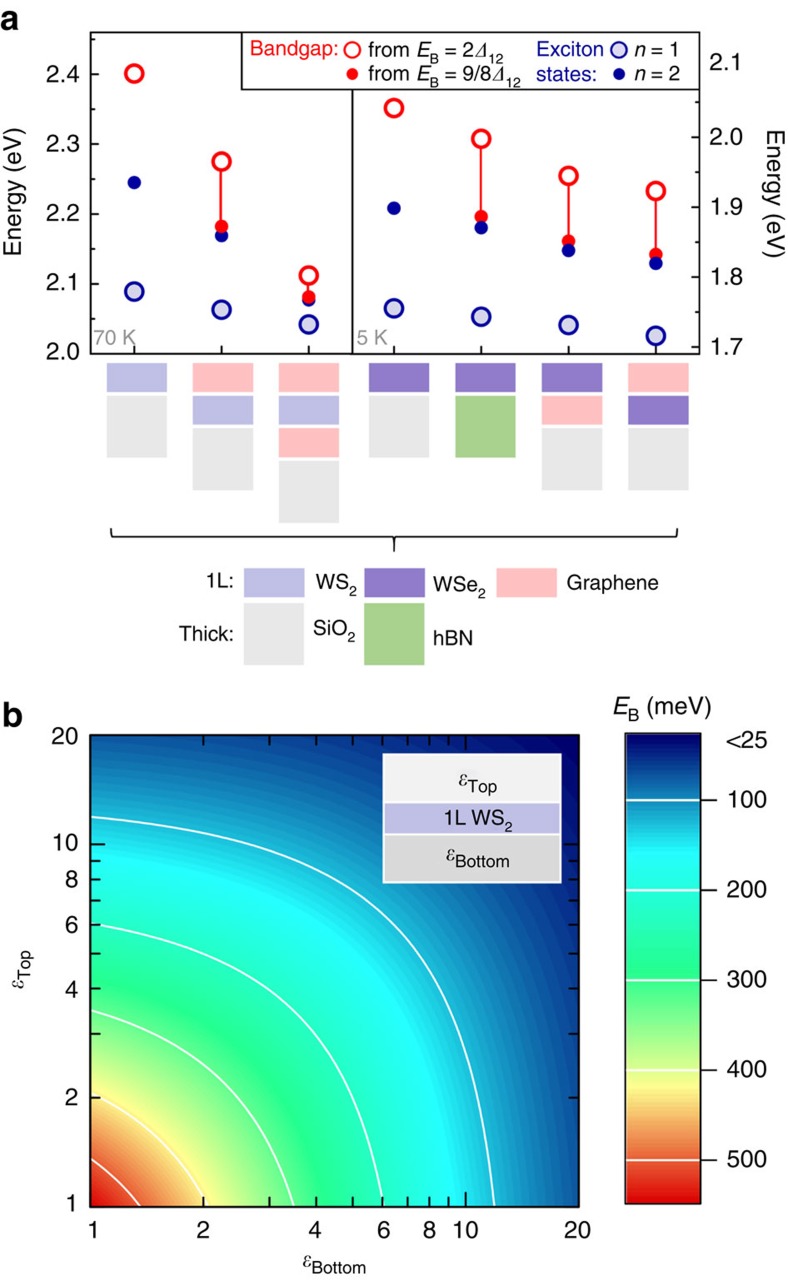
Figure 3. Influence of the choice and configuration of materials on the dielectric tuning of the bandgap.

(a) Experimentally measured exciton ground state (n=1) and the first excited state (n=2) transition energies, as well as the estimated shifts of the bandgap for a variety of heterostructures. Their respective stacking configurations are indicated along the horizontal axis. The bandgap is obtained by adding the exciton binding energy to the measured transition energy of the n=1 state. To estimate the binding energy from the energy separation of the exciton states Δ₁₂, we considered the limiting cases of a non-hydrogenic scaling from ref. 24 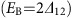and the 2D-hydrogen model 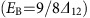. (b) An overview of predicted changes in the exciton binding energy in 1L WS₂, encapsulated between two thick layers of dielectrics. The binding energy E_B is calculated by using the electrostatic approach in the effective mass approximation and presented in a 2D false-colour plot as a function of the top and bottom dielectric constants. The changes in the magnitude of E_B are roughly equal to the corresponding shifts of the bandgap and can reach 500 meV.