Path-sampling strategies for simulating rare events in biomolecular systems

Abstract

Despite more than three decades of effort with molecular dynamics simulations, long-timescale (ms and beyond) biologically relevant phenomena remain out of reach in most systems of interest. This is largely because important transitions, such as conformational changes and (un)binding events, tend to be rare for conventional simulations (< 10 µs). That is, conventional simulations will predominantly dwell in metastable states instead of making large transitions in complex biomolecular energy landscapes. In contrast, path sampling approaches focus computing effort specifically on transitions of interest. Such approaches have been in use for nearly 20 years in biomolecular systems and enabled the generation of pathways and calculation of rate constants for ms processes, including large protein conformational changes, protein folding, and protein (un)binding.

Introduction

Advances in computing hardware and software [1–3] along with record-setting molecular dynamics (MD) simulations, in terms of both length [5] and system size [6] bode well for the future of simulation. Nevertheless, the capacity of MD for investigating long timescales of biological interest remains inadequate, particularly as investigators set their sights on ever larger and more complex systems [7,8].

Path sampling approaches can substantially increase the “reach” of MD in simulating rare events such as protein conformational changes, (un)folding, and (un)binding, by focusing computational effort on the functional transitions rather than the stable states (Figure 1) - without introducing bias in the results. In particular, such approaches exploit the fact that for rare events, the duration of the transition event itself (t_b) is much shorter than the dwell time (t_dwell) in the preceding metastable region (t_b ≪ t_dwell). Even when there is not a clear separation of timescales between t_b and t_dwell, path sampling may offer a considerable advantage over straight-ahead MD, as described in the next section (“Path sampling methods and recent advances”).

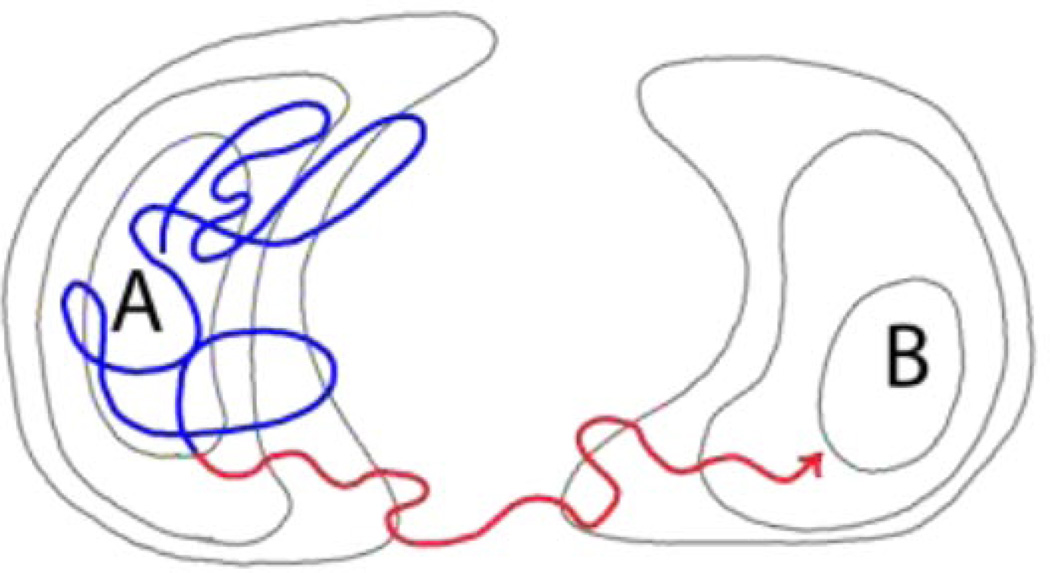
Figure 1.

Rare conformational transitions in MD simulation. A schematized very long MD trajectory which successfully transitions to basin B after starting in A is superimposed over energy contours (grey lines). By definition, every unbiased transition trajectory consists of (i) a dwell period (blue) of duration t_dwell prior to the last exit from the initial state and (ii) the transition event itself (red) of duration t_b. If t_b ≪ t_dwell, then path sampling strategies may be useful in focusing computational effort on the transition process.

In addition to providing rigorous estimates of rate constants, a key strength of path sampling approaches is the generation of an ensemble of transition trajectories. The trajectories themselves yield the full sequence of intermediate configurations of a transition, which are essential for characterizing the mechanism of a complex biological process and too fleeting to be captured by laboratory experiments. Further, the probabilistic description intrinsic to an ensemble quantifies pathway heterogeneity, the importance of which remains to be understood in biomolecular processes of different types.

Path-sampling methods have been advanced significantly in recent years and appear to have reached a state of maturity where theoretical underpinnings have been clarified, and where essential commonalities can be discerned. However, the reader is cautioned that all of the approaches have intrinsic limitations, sketched below, and that path-sampling data must be critically analyzed for undersampling to prevent unfounded interpretation.

We take this opportunity to survey key ideas and recent progress in the field. We cover only approaches that are well-founded in non-equilibrium statistical mechanics and hence capable of yielding, for example, unbiased estimates of rate constants and a true sample of the transition path ensemble. We note that the related Markov state modeling approach will be addressed separately in this issue.

Path sampling methods and recent advances

Conceptual framework

Path sampling approaches exploit the separation of timescales that typically occurs in biomolecular systems. Consider the extreme example of attempting to observe transient unfolding of a stable protein under native conditions: unfolding events will be few and far between. Path sampling approaches can explicitly focus computational effort on the unfolding event, bypassing the lengthy dwells in the folded state.

Path sampling can be useful for rare events even when the separation of timescales is ambiguous. Consider another extreme case where a single uncharged receptor and ligand occupy a large volume, so that the probability of complexation is very small on MD timescales. The time for binding by diffusion arguably is the same as the “transition time” (t_b) in such a system and there is no clear timescale separation. Yet path sampling approaches can focus simulation effort on successful events, and even account for the rareness of binding without bias [*9]. Likewise the conformational sampling of stable states separated by low barriers can be efficiently accomplished using path sampling [10, 78*].

Though path sampling approaches can yield equilibrium state populations and potentials of mean force, their primary strength is a capacity to estimate non-equilibrium observables such as rate constants. In the latter context, the ability to account for directionality and history is critical – particularly tracing back any given trajectory to the most recently occupied state (A or B, “initial” or “target” state), which enables unbiased rate calculation [*11,12,13]; see also [14,15]. This insight from path theory has important practical implications for analyzing ordinary MD simulations and avoiding the Markov assumption [16].

Current path sampling approaches can be divided into the following three categories for conceptual clarity.

Methods using complete paths

Two approaches work directly with complete A-to-B transition paths (Figure 2a). Transition path sampling (TPS) is based on Pratt’s suggestion to run Monte Carlo (MC) simulations on entire trajectories [17] rather than on the more familiar MC for configurations. Advanced by Chandler and coworkers [18–20], TPS uses trial perturbations to an existing A-to-B trajectory and a Metropolis acceptance criterion. Dynamic importance sampling (DIMS), proposed by Woolf [21] based on earlier work [22,23], also uses complete paths. In DIMS, however, independent transition trajectories are generated using biased dynamics, and are then reweighted using the ratio of sampled to true probability [24].

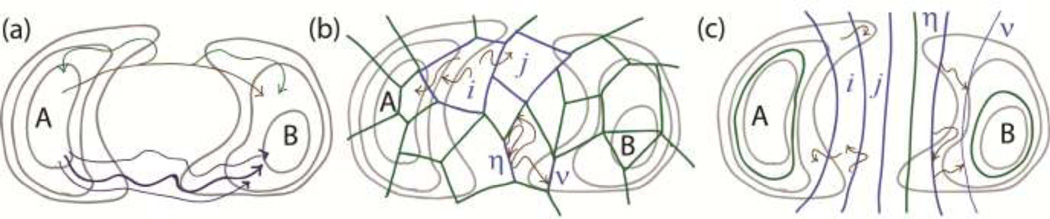
Figure 2.

Schematic basis of path sampling strategies. An energy landscape (grey contours) is shown for which the transition from basin A to B is rare on the timescale of typical MD simulations. (a) Some methods use full-length transition trajectories. In transition path sampling, an initial unphysical trajectory (brown) is perturbed via random trials (green) using a Metropolis Monte Carlo procedure in trajectory space, whereas in dynamic importance sampling, a set of biased trajectories (dark blue) are reweighted to conform with unbiased behavior. (b) Many methods use fully unbiased trajectory segments (brown) connecting bins (i and j), such as the weighted ensemble, or connecting interfaces (η and ν), such as milestoning and non-equilibrium umbrella sampling. (c) Other approaches, such as transition interface sampling and forward flux sampling, use strictly nested interfaces interpolating from A to B. Generally speaking, shorter transitions among bins or interfaces are much more probable than full A-to-B transitions, and trajectory segments can be connected using rigorous statistical mechanics to infer longer-time behavior.

Methods using trajectory segments: region-to-region

Most current path-sampling approaches work procedurally with trajectory segments, even if fully or nearly continuous A-to-B transitions ultimately are produced. As shown in Figures 2b–c, segment-based methods can be categorized accordingly to whether partial transitions are sampled between regions (“bins”) or between interfaces. Bin-to-bin transitions typically are sampled via trajectory segments of fixed duration, whereas interfacial transitions require “catching” trajectories in the act of crossing.

Huber and Kim proposed the weighted ensemble (WE) approach in 1996 [25], which was essentially a rediscovery of the “splitting” strategy described by Kahn in 1951 [26]. The basic idea is to classify configuration space into bins among which transitions are affordably likely. A set of unbiased trajectories is run in parallel, with replication of segments that reach new bins, encouraging progress toward B. Statistical weighting ensures unbiased results [27], and the approach has been extended for steady state and rate-constant calculations [28,*29]. The related adaptive multilevel splitting (AMS) approach uses trajectory splitting within a different statistical formulation without bins [30]. See also [31,32].

Underscoring the methodological convergence occurring in the field, some interfacial approaches have now been adapted for bin-to-bin sampling [33,34]. Markov state models also operate in a bin-to-bin framework (see review by Noe in this issue). The discrete path sampling approach uses energy basins instead of bins [35–37]; see also [38,39].

Approaches using trajectory segments: interface-to-interface

Most current methods sample trajectory segments of heterogeneous lengths that start and end on interfaces. Some approaches require fully nested interfaces that interpolate from initial to target state and others can use nearly arbitrary interfaces – surfaces of arbitrary bins tiling configuration space (Figure 2b–c).

With transition interface sampling (TIS), van Erp, Moroni, and Bolhuis [*11] introduced an extension of TPS which attempted to improve the rate-constant calculation by using a series of partial-flux calculations for a set of nested interfaces separating states A and B – see Figure 2c. Intermediate TPS calculations are used to generate the necessary TIS path ensembles. There have been a number of TIS extensions [40,41]. Forward flux sampling (FFS) uses a similar formalism but instead runs standard (not TPS) simulations between interfaces [42], and FFS has been generalized [33]. See also [43].

Interfaces which may not be nested (e.g., boundaries of Voronoi cells – see Figure 2b) are used in some approaches. Non-equilibrium umbrella sampling (NEUS), introduced by Dinner and coworkers, first showed how to use interfaces for arbitrary cells which tile configuration space in steady-state calculations [44] and was further developed [13,45,46]. Milestoning, although originally introduced by Faradjian and Elber for nested interfaces [47], was later generalized for use with arbitrary interfaces [48,49].

Limitations

All the approaches discussed here share the goal of generating an ensemble of transition trajectories, and hence they also share certain limitations. The focusing of sampling on transition regions instead of stable states in an unbiased manner typically requires that the transition trajectories are correlated with one another (e.g., [19,27]). Such correlations imply a reduction in information content: perhaps one in 100 transitions is truly independent. Therefore, trajectories should be analyzed carefully for correlations and sampling quality [49, 11*, 29*, 9*]. For methods where the path-sampled trajectories are not correlated, there generally is another type of statistical inefficiency [24].

Another practical concern regards software. Several path-sampling packages are publicly available [*50,51–53], and most require some parameter tuning. Algorithms which examine trajectories at fixed time intervals, such as WE, lend themselves to facile interoperability with a variety of MD engines. Interface-based methods require “catching” trajectories in the act of crossing boundaries, which already has been hard-wired in some packages [53,54], but could represent a significant barrier for users desiring alternative dynamics.

Successes

In recent years, path sampling approaches have enabled the simulation of several types of long-timescale biological processes that would not have been practical using conventional simulation: large protein conformational transitions, protein folding, and protein-ligand (un)binding.

Protein conformational transitions and folding processes

Notable successes involving large protein conformational transitions include simulations of substrate-induced conformational changes in enzymes and large conformational transitions in membrane transport proteins. In studies involving enzymes, milestoning has generated ms conformational transitions between the open and closed states of the HIV reverse transcriptase [*4,55], yielding rate constants that are consistent with experiment (Figure 3a). In studies involving membrane transport proteins, the WE approach has generated pathways for outward-to-inward-facing transitions in the sodium symporter Mhp1 using coarse-grained simulations [56] and the DIMS approach has generated transitions between the cytoplasmic open conformation and perisplamic open conformation of the lactose permease transporter using atomistic simulations in implicit solvent [57]. For the related problem of ion permeation, the WE approach has enabled the calculation of current-voltage relationships for a simple model ion channel [77].

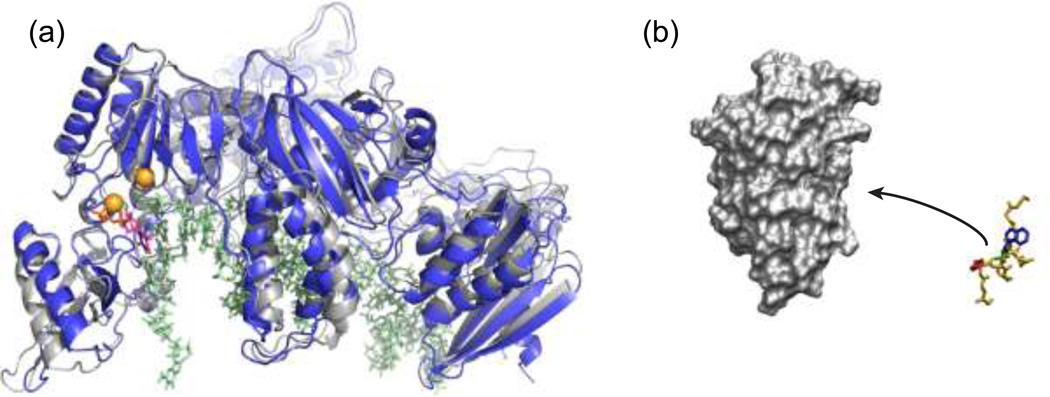
Figure 3.

Path sampling successes. a) Milestoning has generated pathways and calculated rate constants for substrate-induced transitions between the open (gray) and closed (blue) conformations of HIV reverse transcriptase transcriptase in complex with Mg²⁺ ions (yellow) and duplex DNA (green); for clarity, only the p66 subunit is shown, although both p66 and p51 subunits were included in the simulations [*4]. b) The WE approach has generated pathways and calculated rate constants for the protein-peptide binding process involving the MDM2 protein (gray) and an intrinsically disordered p53 peptide (yellow) [*78].

Applications of path sampling approaches to protein folding – the most extreme protein conformational transition – have been focused on mini-proteins that fold on the µs timescale. For example, the single-replica multistate TIS method has enabled efficient simulation of both folding and unfolding processes for Trp-cage [58] while the FFS method has been used to simulate a loop unfolding transition in Trp-cage [59] that was revealed by a previous TIS study to be rate-limiting for the unfolding process [60]. In addition, the single-replica multistate TIS method has been applied to the µs-folding process of the villin headpiece as well as its much slower sub-ms unfolding process (mean first passage time of 0.8 ms), demonstrating that path sampling approaches can be effective in estimating rate constants for protein unfolding processes as well as folding processes [61]. Of future interest are the application of these approaches to the (un)folding processes of entire proteins (e.g., NTL9 and ubiquitin) at experimental temperatures; due to their longtimescales (ms or beyond), such folding processes have typically been characterized at the (considerably higher) melting temperatures by straightforward simulations [62,63].

Protein (un)binding processes

The characterization of protein (un)binding mechanisms is not only fundamental to biology, but of great interest to the field of drug design. The simulation of protein binding processes with rigorous kinetics is particularly challenging due to the presence of metastable intermediates (e.g., the encounter complex).

Path sampling has yielded initial successes with models at different levels of resolution. For example, the WE approach has enabled the first atomistic simulations (to our knowledge) of protein-peptide binding pathways with rigorous rate constants; these simulations involved the MDM2 protein and an intrinsically disordered p53 peptide, which adopts an α-helical conformation upon binding MDM2 [78*]. In addition, two studies have demonstrated the power of path sampling strategies in generating atomistic pathways for protein-ligand unbinding processes and the corresponding k_off values, which are of great interest for drug design efforts. These studies involve a) the application of the WE approach to the FK506 binding protein and several low-affinity, small-molecule inhibitors, which unbind on timescales up to tens of ns, resulting in the first analysis of ligand-exit distributions [*64], and b) the application of the AMS approach to trypsin and the benzamidine inhibitor, which unbinds on the ms timescale [65]. In addition, it has been demonstrated that experimental k_on values can be efficiently reproduced for various protein-ligand systems using milestoning as part of an atomistic MD/Brownian Dynamics approach [66].

Even coarse-grained models may not be amenable to complete sampling via straight-ahead simulation. For example, the WE strategy has been of great benefit to even Brownian Dynamics simulations involving coarse-grained, albeit flexible protein models that have been parameterized to reproduce the molecular shapes, electrostatic potentials, and diffusion properties of all-atom models. The resulting WE simulations enabled not only the efficient reproduction of experimental k_on values for wild-type and mutant complexes of barnase and barstar, but a statistically robust estimate of the much slower “basal” k_on involving the hydrophobic isosteres of the two proteins – a quantity of fundamental interest to the field of molecular recognition [*9] (Figure 3b).

Challenges

As path sampling approaches are used to target more complex systems and slower processes, which seems inevitable, a number of challenges remain. The most basic difficulty hinges on intrinsic timescales of the systems themselves: for example, if the transition event duration (see Introduction) for a certain process exceeds 1 µs, then sampling an ensemble of uncorrelated transition events would be almost impossible given a total budget of 10 µs. Of course, the intrinsic timescales would not be known ahead of time, suggesting caution is necessary for complex systems.

Coordinates and correlations present the primary methodological challenge. The problem of generating correlated transition trajectories was discussed above in “Path Sampling Methods and Recent Advances”, but it is closely connected to the difficulty of constructing suitable coordinates (or bins or interfaces) for methods requiring them. Consider a system which is not readily described by a one-dimensional reaction coordinate (i.e., which has slow orthogonal coordinates). If one-dimensional bins or interfaces are used, it can be expected that fully sampling the orthogonal space will be slow and may render the results unreliable – the sampled trajectory segments may be overly correlated. Fortunately, investigators are already beginning to make progress in adaptively developing bins and interfaces [27,67,68].

It will be important to develop software resources further. As noted in Section II, several highly scalable packages are currently available, including WESTPA, AWE-WQ and FRESHS, which have demonstrated inter-operability with a variety of dynamics engines [*50,52,69]. A competitive software ecosystem with additional robust packages should be a boon to the field. Nevertheless, we caution that path sampling tools are likely to continue to require considerable user expertise in yielding reliable results.

On a final note, another frontier that has already been addressed by initial studies is the application of path sampling approaches to problems at other scales. Several approaches have already been applied to signaling networks, gene regulation, and spatially resolved cell models [42,70–76].

Highlights.

• Advances, common features, and remaining challenges are presented for path sampling approaches.

• Key strengths are the efficient calculation of transition trajectories and rate constants.

• Successful applications include protein conformational changes, (un)folding and (un)binding.