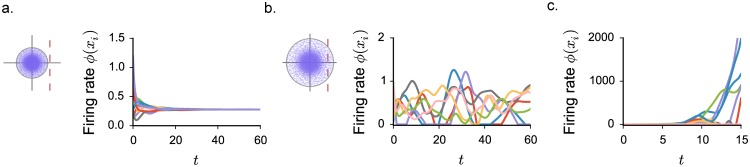
Fig 1. Dynamical regimes of an excitatory-inhibitory network of threshold-linear units as the coupling is increased.
Numerical integration of the dynamics in Eq (1), firing rates of randomly chosen units. In the insets: complex eigenspectrum of the fixed point stability matrix, the red line corresponding to the stability bound. a. Weak coupling regime: the network activity converges to the homogeneous fixed point. b. Intermediate coupling regime: the activity displays stable fluctuations in time and across different units. c. Strong coupling regime: in absence of an upper bound, activity diverges. Choice of the parameters: g = 4.5, C = 100. N = 2000, no saturating upper bound: ϕmax → ∞. In this and all other figures, all quantities are unitless (see Methods).