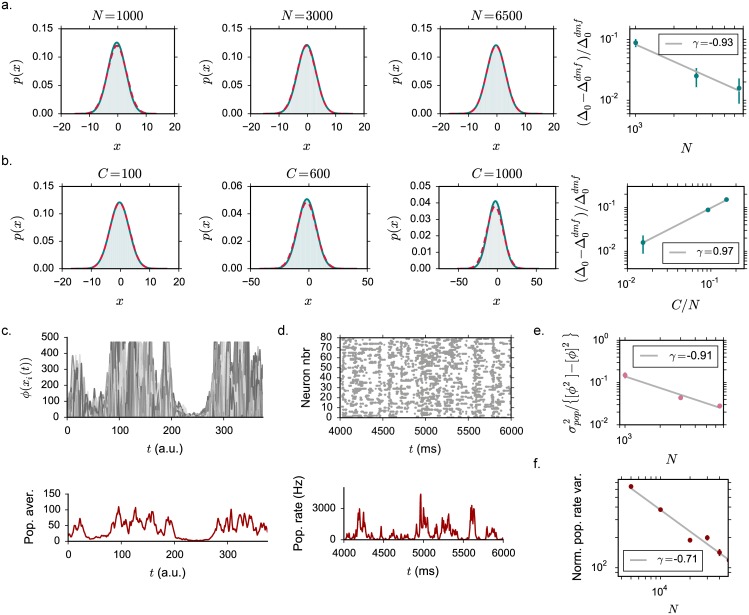
Fig 11. Comparison between dynamical mean field predictions and numerical simulations: Finite size effects.

a. Dependence on the system size N (C = 100). In the first three panels: distribution of the input current x in the population and in different time steps. The numerical distribution is obtained through averaging over 3 realizations of the synaptic matrix. Light green: simulated data distribution, dark green: best Gaussian fit to data, red: DMF prediction. In the fourth panel: normalized deviations from the DMF theoretical value. The log-log dependence is fitted with a linear function, γ giving the coefficient of the linear term. Choice of the parameters: g = 4.1, J = 0.2, ϕ_max = 2. b. As in a, dependence on the in-degree C (N = 6500). c. Finite size effects in rate networks with large saturation upper-bound: sample of network activity (top: single units in grey scale, bottom: population averaged firing rate). Choice of the parameters: g = 5, J = 0.14, ϕ_max = 240. d. Finite size effects in networks of LIF neurons with small refractory period: sample of network activity (rastergram of 80 randomly selected neurons, population averaged firing rate). Choice of the parameters: N = 20000, C = 500, g = 5, τ_rp = 0.01 ms, J = 0.9 mV. e. Finite size effects in rate networks with large saturation upper-bound: normalized variance of the population-averaged firing rate as a function of the network size. f. Finite size effects in networks of LIF neurons with small refractory period: normalized variance of the population-averaged firing rate as a function of the network size (computed with 1 ms bins).