Rate-Dependent Role of I_Kur in Human Atrial Repolarization and Atrial Fibrillation Maintenance

Abstract

The atrial-specific ultrarapid delayed rectifier K⁺ current (I_Kur) inactivates slowly but completely at depolarized voltages. The consequences for I_Kur rate-dependence have not been analyzed in detail and currently available mathematical action-potential (AP) models do not take into account experimentally observed I_Kur inactivation dynamics. Here, we developed an updated formulation of I_Kur inactivation that accurately reproduces time-, voltage-, and frequency-dependent inactivation. We then modified the human atrial cardiomyocyte Courtemanche AP model to incorporate realistic I_Kur inactivation properties. Despite markedly different inactivation dynamics, there was no difference in AP parameters across a wide range of stimulation frequencies between the original and updated models. Using the updated model, we showed that, under physiological stimulation conditions, I_Kur does not inactivate significantly even at high atrial rates because the transmembrane potential spends little time at voltages associated with inactivation. Thus, channel dynamics are determined principally by activation kinetics. I_Kur magnitude decreases at higher rates because of AP changes that reduce I_Kur activation. Nevertheless, the relative contribution of I_Kur to AP repolarization increases at higher frequencies because of reduced activation of the rapid delayed-rectifier current I_Kr. Consequently, I_Kur block produces dose-dependent termination of simulated atrial fibrillation (AF) in the absence of AF-induced electrical remodeling. The inclusion of AF-related ionic remodeling stabilizes simulated AF and greatly reduces the predicted antiarrhythmic efficacy of I_Kur block. Our results explain a range of experimental observations, including recently reported positive rate-dependent I_Kur-blocking effects on human atrial APs, and provide insights relevant to the potential value of I_Kur as an antiarrhythmic target for the treatment of AF.

Introduction

The ultrarapid delayed rectifier K⁺ current (I_Kur) was originally described as a rapidly activating, 4-aminopyridine-sensitive K⁺ current with slow and limited inactivation (1). However, many of the original experiments used relatively short test pulses, typically <4 s long, which may have not been enough to observe the full extent of I_Kur’s inactivation. Feng et al. (2), using longer 50-s test pulses, showed that I_Kur inactivates almost completely when the cell is depolarized to +40 mV, with a biexponential time course comprising fast (τ_f) and slow time constants (τ_s) of 1.0 and 6.8 s, respectively. Based on these experiments, it has been hypothesized that I_Kur inactivation may play an important role under physiological conditions, specifically related to I_Kur frequency-dependent dynamics (2). The potential for full inactivation of I_Kur suggests that the contribution of the current would decrease at faster rates, as the total amount of time when the cell is depolarized increases and inactivation accumulates. However, recent experimental results using the I_Kur-selective blocker XEN-D0103 suggest the opposite, and indicate that the contribution of I_Kur to atrial repolarization increases at higher rates (3).

To our knowledge, none of the commonly used mathematical models of the human atrial cardiomyocyte action potential (AP) integrate the experimentally defined I_Kur inactivation dynamics reported by Feng et al. (2). To better understand the rate-dependent role of I_Kur and the effect of blocking it on the human atrial AP, it is necessary to use a model with accurate inactivation properties. In this study, we sought to 1) quantify the kinetic features of the I_Kur inactivation properties defined by Feng et al. (2); 2) update the Courtemanche human atrial AP model (4) to include realistic I_Kur inactivation parameters; 3) investigate the rate-dependent properties of I_Kur inactivation over the course of the AP under physiological conditions; 4) evaluate the contribution of I_Kur with realistic inactivation properties to human atrial repolarization at different frequencies; and 5) evaluate the potential consequences for effects of blocking I_Kur on atrial fibrillation (AF) in non-remodeled and AF-remodeled atrial tissue.

Materials and Methods

Mathematical modeling of I_Kur inactivation

The experimental data recorded by Feng et al. (2) were used as the basis for model development in our study. A description of the experimental methods can be found in the original article (2). The Courtemanche human atrial cardiomyocyte model was implemented (4). The original formulation of the I_Kur inactivation parameter is as follows:

$${\text{I}}_{\text{Kur}}=C_m\times g_{\text{Kur}}\times u_a^3\times u_i\times \left(V-E_K\right),$$

$$g_{\text{Kur}}=0.005+\frac{0.05}{1+\text{exp}\left(-\frac{V-15}{13}\right)},$$

$${\alpha }_{ui}={\left[21+\exp \left(-\frac{V-185}{28}\right)\right]}^{-1},$$

$${\beta }_{ui}=\exp \left(\frac{V-158}{16}\right),$$

$${\tau }_{ui}={\left[{\alpha }_{ui}+{\beta }_{ui}\right]}^{-1}/K_{\text{Q}10},$$

$$u_{i,\infty }={\left[1+\exp \left(\frac{V-99.45}{27.48}\right)\right]}^{-1},$$

$$\frac{\text{d}{u}_i}{\text{d}t}=\frac{u_{i,\infty }-u_i}{{\tau }_{ui}},$$

where I_Kur is the ultrarapid delayed rectifier K⁺ current, g_Kur is the maximal I_Kur conductance, V is the transmembrane potential, E_K is the K⁺ equilibrium potential, and u_a and u_i are I_Kur’s activation and inactivation gating variables, respectively; α_ui and β_ui are the forward and backward rate constants for the inactivation gate variable, respectively; τ_ui is the time constant; u_i,∞ is the steady-state relation for the inactivation gate variable; C_m is the membrane capacitance (100 pF); and K_Q10 is a scaling factor (3).

To account for I_Kur inactivation dynamics we replaced the original inactivation gating variable u_i by fast (u_i,f) and slow (u_i,s) inactivation gating variables. The gating variables and time constant parameters were fitted by iteratively minimizing the mean error of the model time constants relative to experimentally derived values obtained with a 50-s test-pulse at 0, 10, 20, 30, 40, and 50 mV (Fig. S1, B and C); the modified inactivation gating variables and time constants are given by the following:

$${\tau }_{ui,f}=800\times (2-\left[\frac{V}{40}\right]),$$

$$u_{i,f\infty }={\left[1+\exp \left(\frac{V-35}{20}\right)\right]}^{-1},$$

$${\tau }_{ui,s}=5800\times {\left[1+\exp \left(-\frac{V+80}{11}\right)\right]}^{-1},$$

$$u_{i,s\infty }={\left[1+\exp \left(\frac{V+5}{5}\right)\right]}^{-1},$$

$$\frac{\text{d}{u}_{i,x}}{\text{d}t}=\frac{u_{i,x\infty }-u_{i,x}}{{\tau }_{ui,x}},$$

$${\text{I}}_{\text{Kur}}=C_m\times g_{\text{Kur}}\times u_a^3\times u_{i,s}\times u_{i,f}\times \left(V-E_K\right).$$

The activation gating variable and time constant were not modified and are given by the following:

$${\tau }_{ua}={\left[{\alpha }_{ua}+{\beta }_{ua}\right]}^{-1}/K_{\text{Q}10},$$

$${\alpha }_{ua}=0.65{\left[\text{exp}\left(-\frac{V+10}{8.5}\right)+\text{exp}\left(-\frac{V-30}{59}\right)\right]}^{-1},$$

$${\beta }_{ua}=0.65{\left[2.5+\text{exp}\left(\frac{V+82}{17}\right)\right]}^{-1},$$

$${\tau }_{ua}={\left[{\alpha }_{ua}+{\beta }_{ua}\right]}^{-1}/K_{\text{Q}10},$$

$$u_{a,\infty }={\left[1+\text{exp}\left(-\frac{V+30.3}{9.6}\right)\right]}^{-1}.$$

The activation gate open probability is given by u_a³. The inactivation gate open probability in the original model was given by u_i; in the modified model u_i,s × u_i,f was used to reflect the combined effects of slow and fast inactivation components. Open probabilities range from 0 (closed) to 1 (open). The charge carried by I_Kur in one cardiac cycle, given by the area under the I_Kur-versus-time curve (Kur AUC), was calculated by integrating I_Kur over one cardiac cycle. The activation gate open-probability area under the curve (u_a³ AUC) was calculated by integrating u_a³ over one cardiac cycle. The AP amplitude was defined as the difference between the peak phase-0 overshoot potential and the resting membrane potential.

Mathematical simulations

The Courtemanche model of human atrial cardiomyocyte bioelectricity was implemented with the original and updated I_Kur inactivation formulations. The total ionic current for the model (I_tot) was given by the following:

$${\text{I}}_{\text{tot}}={\text{I}}_{\text{Na}}+{\text{I}}_{\mathrm{K}1}+{\text{I}}_{\text{to}}+{\text{I}}_{\text{Kur}}+{\text{I}}_{\text{Kr}}+{\text{I}}_{\text{Ks}}+{\text{I}}_{\text{Ca},\text{L}}+{\text{I}}_{\text{p},\text{Ca}}+{\text{I}}_{\text{NaK}}+{\text{I}}_{\text{NaCa}}+{\text{I}}_{\text{b},\text{Na}}+{\text{I}}_{\text{b},\text{Ca}}+{\text{I}}_{\text{K},\text{ACh}},$$

where I_Na is the fast inward Na⁺ current; I_K1 is the inward rectifier K⁺ current; I_to is the transient outward K⁺ current; I_Kur, I_Kr, and I_Ks are the ultrarapid, rapid, and slow components of the delayed rectifier K⁺ current, respectively; I_Ca,L is the L-type inward Ca²⁺ current; I_p,Ca is the sarcolemmal Ca²⁺ pump current; I_NaK is the Na⁺/K⁺ pump current; I_NaCa is the Na⁺/Ca²⁺ exchanger current; I_b,Na is the background Na⁺ current; I_b,Ca is the background Ca²⁺ current; and I_K,ACh is the acetylcholine-activated K⁺ current (5). Isolated cardiomyocyte APs were simulated at 37°C by numerical integration with the software MATLAB’s ODE23s ordinary differential equation solver (The MathWorks, Natick, MA) with a relative tolerance of 10⁻². For each condition, pacing was sustained for 280 cycles with 2-ms 3 nA stimuli and the last action potential was used for analysis.

Computer simulations of the effect of I_Kur block on AF were performed with the CARP simulator, which solves the monodomain equation by the finite element method as described previously (6), as follows:

$$\nabla \times {\sigma }_i\nabla V=\beta \left(C_m\frac{\partial V}{\partial t}+I_{\text{tot}}\right),$$

where σ_i is the tissue conductivity, β is the membrane surface-to-volume ratio (0.14 μm⁻¹), and C_m is the membrane capacitance (1 μF/cm²). The updated Courtemanche ionic model was adapted and implemented in CARP. Conductivities were chosen to give a physiological conduction velocity in the longitudinal direction (47.9 cm/s). The tissue measured 7 × 6 cm with fibers oriented along the long dimension with an anisotropy ratio of ∼6. The grid was discretized at 100-μm resolution and equations solved with a 25-μs timestep. Reentry was initiated by a standard S1-S2 cross-shock protocol with an S1-S2 interval of 170 ms.

Two-dimensional simulations were conducted using three different acetylcholine (ACh) distribution patterns (one homogeneous ACh distribution and two sinusoidal distributions) and three peak ACh concentrations (1.875, 3.75, and 7.5 nM), generating nine conditions. I_Kur block was simulated by a fixed reduction in maximal I_Kur conductance (g_Kur). Dose-response curves were generated by introducing I_Kur block at 10 different time-points {t_drug = 1000 ms, 1100 ms, … 1800 ms, 1900 ms} for each percent I_Kur block {10%, 20%, …, 90%, 100%}; the average time to termination was quantified as the time from t_drug to reentry termination. Simulations were run using the control (non-remodeled) Courtemanche human atrial AP model and repeated with an AF-remodeled AP model consisting of the control model with the following modifications: I_to conductance reduced by 50%, I_Kur conductance reduced by 50%, I_Ca,L conductance reduced by 70%, and I_K1 conductance increased by 100% (7).

Results

Experimentally observed time-dependent inactivation of I_Kur

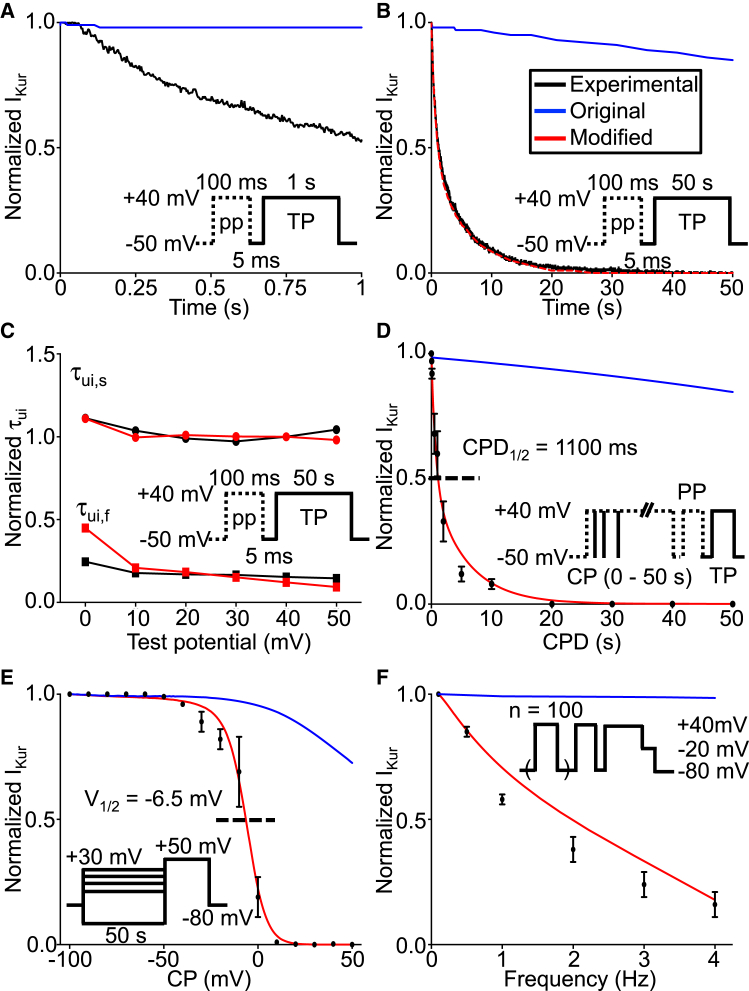
The ultrarapid delayed rectifier K⁺ current (I_Kur) is often described as having slow and partial inactivation. Fig. 1 A shows normalized I_Kur during a 1000 ms test-pulse to +40 mV, 5 ms after a 100-ms pretest pulse to +40 mV to inactivate I_to, as recorded experimentally (black) (2) and from the original Courtemanche human atrial I_Kur formulation (blue). Using this relatively short test pulse, experimental I_Kur inactivates by ∼45% (black). In contrast to experimental data, in the original Courtemanche model, I_Kur does not inactivate appreciably over the course of the pulse (blue). Fig. 1 B shows normalized I_Kur during a longer, 50 s test-pulse to +40 mV, 5 ms after a 100-ms pretest pulse to +40 mV to inactivate I_to. With the longer pulse, the experimentally recorded I_Kur (black) inactivated completely with a biexponential time-course characterized by fast and slow time constants of 702 ± 7 and 5688 ± 26 ms, respectively. Again, the original Courtemanche model (blue) fails to reproduce I_Kur’s inactivation dynamics, with 85% of the peak current persisting at the end of the 50-s test-pulse.

Figure 1.

Time-, voltage-, and frequency dependence of I_Kur inactivation. (A) Shown here is the normalized I_Kur current during a 1000-ms test pulse (TP) at +40 mV, 5 ms after a 100-ms prepulse (PP), to inactivate I_to (inset) as recorded from the experimental preparation (black) and the original Courtemanche human atrial model (blue). (B) Normalized I_Kur current using a similar protocol, but with test pulse duration of 50 s as recorded from the experimental preparation (black) and the original and modified Courtemanche model (blue and red, respectively), is given. The experimental and modified model time constants are τ_ui,f,exp = 702 ± 7 ms, τ_ui,s,exp = 5688 ± 26 ms and τ_ui,f,model = 713 ± 18 ms, τ_ui,s,model = 5848 ± 188 ms, respectively. (C) Normalized fast (τ_ui,f) and slow (τ_ui,s) time constants as a function of test pulse potential for the experimental preparation and the modified Courtemanche model at 37°C are shown. (D) Shown here is the normalized I_Kur current using a CPD to +40 mV, followed by a 100-ms prepulse (PP) to +40 mV to inactivate I_to preceding a 100-ms test pulse (TP) to +40 mV (inset), as recorded from the experimental preparation and the original and modified models; the half-inactivation CPD (CPD_1/2) was 1100 ms. (E) Shown here is the normalized I_Kur current using a 50 s-conditioning pulse (CP) to various voltages followed by a 240-ms test pulse to +50 mV (inset); the half-inactivation voltage (V_1/2) was –6.5 mV in the model and –7.5 ± 0.6 mV experimentally. (F) Shown here is the normalized I_Kur current obtained by applying 100 pretest stimuli of 100 ms duration at +40 mV at various frequencies, followed by a 100-ms conditioning pulse to +40 mV to inactivate I_to and a 140-ms test pulse to +40 mV (inset); the normalized current at 4 Hz was 16% of its value at 0.1 Hz. For all panels, experimental data are in black; original and modified models are in blue and red, respectively.

Model inactivation kinetics modified according to experimental data

To accurately reproduce the experimentally recorded I_Kur inactivation kinetics, we modified the Courtemanche model by introducing a set of slow (u_i,s) and fast (u_i,f) inactivation gating variables in place of the single inactivation gating variable (u_i) in the original model. The voltage dependence of the inactivation gating variables for the original (u_i,original, blue line) and modified (u_i,f, red solid line; u_i,s, red dashed line) models is shown in Fig. S1 A. The major modification to inactivation gating is more complete inactivation at depolarized potentials; the complete mathematical formulation can be found in Materials and Methods. We also replaced the inactivation time constant (τ_ui,original) with a set of fast (τ_ui,f) and slow (τ_ui,s) inactivation time constants (Fig. S1 B). Note that the updated inactivation time constants are of the order of 1–6 s. The voltage dependence of the activation gating variable (Fig. S1 C; u_a,x) and activation time constant (Fig. S1 D, τ_ua,x) were not modified. The activation time constant is in the range of 1–6 ms.

The modified model (red line) closely reproduced the experimentally recorded current inactivation (black line) during a prolonged pulse (Fig. 1 B) and the experimentally recorded I_Kur inactivation kinetics (Fig. 1 C) at 37°C. Excellent agreement between experiments and the mathematical model was obtained across the spectrum of test potentials.

Time-, voltage-, and frequency dependence of I_Kur inactivation

We then compared the time dependence of I_Kur inactivation in the model to experimental results obtained by varying the duration of the test pulse. Fig. 1 D (black) shows experimentally recorded normalized I_Kur obtained with conditioning pulses to +40 mV of varying durations, followed by a 100-ms prepulse to +40 mV to inactivate I_to and then a 100-ms test pulse to +40 mV. I_Kur displayed complete inactivation with conditioning pulses >20 s. In contrast, the original Courtemanche model-derived results showed little inactivation even with the longest conditioning-pulse duration (Fig. 1 D, blue). Conversely, the modified model closely replicated the experimental data (Fig. 1 D, red); the half-inactivation conditioning pulse duration (CPD_1/2) was 1100 ms at +40 mV. The voltage dependence of I_Kur inactivation was then assessed by applying a 50 s pretest pulse to various voltages followed by a 240-ms test pulse to +50 mV; the experimentally recorded normalized I_Kur is shown in Fig. 1 E (black). I_Kur inactivation is highly dependent on the pretest pulse potential. The original Courtemanche model (blue) did not reproduce the experimentally observed voltage-dependent inactivation dependence (Fig. 1 E, black), whereas the modified model-generated results (red) closely matched experimental findings. The experimental and modified-model half-inactivation voltages (V_1/2s) were −7.5 ± 0.6 and −6.5 mV, respectively.

The frequency dependence of I_Kur inactivation was studied by applying 100 pulses of 100-ms duration to +40 mV at various frequencies, followed by a 100-ms conditioning pulse to +40 mV to inactivate I_to and a 140-ms test pulse to +40 mV. Experimentally, I_Kur displayed marked frequency dependence with 84% reduction at 4 vs. 0.1 Hz (Fig. 1 F, black data). In contrast, the original Courtemanche model showed virtually no frequency dependence (Fig. 1 F, blue). The modified model was much more consistent with the experimental findings (Fig. 1 F, red).

Incorporation of realistic I_Kur inactivation kinetics and AP dynamics

Fig. S2 shows the AP amplitude (Fig. S2 A), AP duration at 90% repolarization (APD₉₀, Fig. S2 B), transmembrane potential at the time of maximum phase 0 overshoot (overshoot potential, Fig. S2 C), and phase-0 peak Na⁺ current (peak I_Na, Fig. S2 D) as a function of cycle length (CL) for the original (black) and modified (red) Courtemanche models. Despite markedly different I_Kur inactivation kinetics, there were no significant differences in AP or Na⁺-current dynamics between the two models across a wide range of physiologically relevant cycle lengths. We then pursued the rate-dependent properties of I_Kur to understand why, despite much greater inactivation for both experimental and model pulse protocols than in the original Courtemanche model, there was no apparent effect on rate-dependent AP properties.

I_Kur activation and inactivation dynamics and mechanisms of rate-dependence

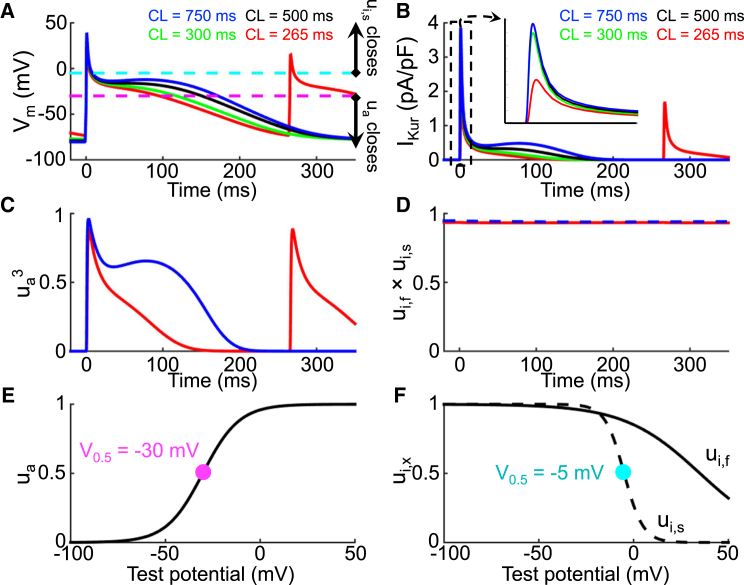
Fig. 2 A shows model APs at progressively shorter stimulation cycle lengths (750, 500, 300, and 265 ms). The AP duration is shortened and plateau potential becomes less positive as the dome disappears when stimulation cycle length decreases. Fig. 2 B shows the corresponding I_Kur simulations. There is a rate-dependent decrease in I_Kur during phase 2 of the AP with little change in peak I_Kur (inset) except at the shortest cycle length (inset, red). Fig. 2, C and D, shows the corresponding activation and inactivation gate open probabilities (u_a³; u_i,f × u_i,s) as a function of time for the shortest (red) and longest (blue) cycle length. I_Kur activation decreases during phase 2 in a rate-dependent manner (Fig. 2 C), whereas inactivation is virtually rate independent (Fig. 2 D). Therefore, I_Kur rate dependence is driven by its activation gate kinetics, with little contribution from inactivation. This is further detailed in Fig. S3 where the rate dependence of the total I_Kur charge carried per cycle (Fig. S3 B) is shown to be due to changes in rate-dependent activation-gate open probability (Fig. S3 F), with no significant contribution from inactivation (Fig. S3 D).

Figure 2.

Mechanism of I_Kur rate dependence. (A) Action potentials at stimulation cycle lengths from 265 ms (red), 300 ms (green), 500 ms (black), and 750 ms (blue) are shown. The purple and teal dashed lines correspond to the activation and inactivation gating variable 50% (V_0.5,ua = −30 mV and V_0.5,uis = −5 mV) opening potentials, respectively. (B) Shown here are corresponding I_Kur tracings; there is a rate-dependent decrease in I_Kur during phase 2 of the AP. (C) Shown here is the activation gate open probability (u_a³) and (D) inactivation gate open probability (u_i,f × u_i,s) as a function of time for CLs of 265 ms (red) and 750 ms (blue). The activation open probability is rate dependent and the inactivation open probability is rate independent. (E) Shown here is the activation gating variable (u_a) as a function of transmembrane potential; the purple dot corresponds to activation gating variable V_0.5 as transposed on (A). (F) Fast (u_i,f; black solid) and slow (u_i,s; black dashed) inactivation gating variables as a function of transmembrane potential are given; the teal dot corresponds to the slow inactivation gating variable V_0.5 as transposed on (A). The inactivation open probability is rate independent because the action potential spends very little time positive to V_0.5,uis (−5 mV; teal).

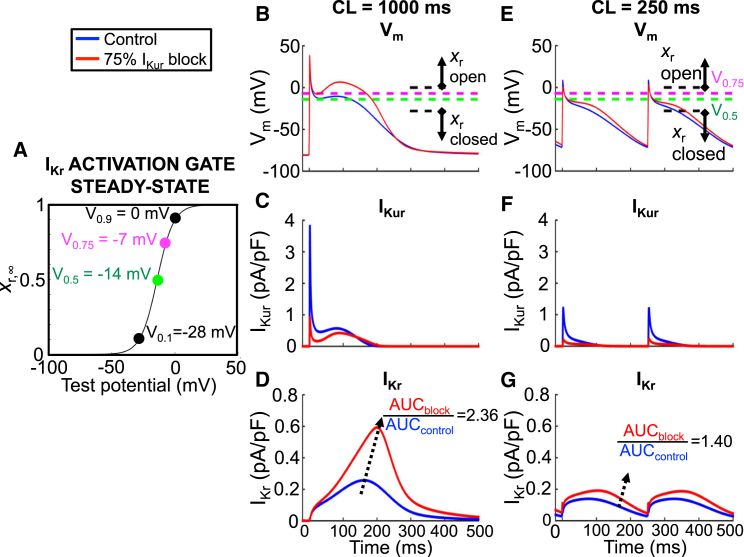
Figure 3.

Rate-dependent effects of I_Kur block on the AP. (A) Shown here is the I_Kr activation gate steady state (x_r,∞) as a function of test potential. V_0.1, V_0.5, V_0.75, and V_0.9 are marked and transposed onto (B) and (E) as dashed lines. (B) Shown here are APs obtained at a cycle length of 1000 ms under control (blue) and with 75% I_Kur blockade (red); the AP duration at −60 mV (APD₋₆₀) was 255 ms for both. (C and D) Shown here are corresponding I_Kur and I_Kr tracings; the ratio of I_Kr with 75% I_Kur block to control was 2.36. (E) Shown here are APs obtained at a cycle length of 250 ms under control (blue) and with 75% I_Kur blockade (red); the APD₋₆₀ for control and 75% I_Kur block was 199 and 209 ms, respectively. (F and G) Shown here are corresponding I_Kur and I_Kr tracings; the ratio of I_Kr with 75% I_Kur block to control was 1.40.

Fig. 2 E shows the steady-state activation gating variable as a function of transmembrane potential with the voltage for 50% (V_0.5 = −30 mV) activation marked with a purple dot; V_0.5 is shown in Fig. 2 A as a purple dashed line. For membrane potentials negative to V_0.5, the activation gate starts to close, whereas for potentials positive to V_0.5, the activation gate is mostly open. The activation-variable (u_a³; Fig. 2 C) rate dependence can be understood based on the AP time course (Fig. 2 A) and u_a’s voltage dependence (Fig. 2 E). At slower stimulation frequencies like a cycle length of 750 ms (blue curve in Fig. 2 A), the plateau potential is positive to V_0.5 (dashed purple line in Fig. 2 A) for the duration of phase 2 of the AP, keeping u_a largely open. It is only at the end of the AP plateau that the membrane potential falls below V_0.5, leading to appreciable decreases in u_a and return of the activation gate open probability toward 0 (u_a³ = 0, closed, Fig. 2 C). In contrast, at faster stimulation frequencies such as at a cycle length of 265 ms (red curve in Fig. 2 A), the plateau potential is negative to V_0.5 starting at the end of phase 1 (Fig. 2 A), leading to earlier and more rapid closure of the activation gate (red curve in Fig. 2 C). The activation-gate time constant is in the range of 1–6 ms (Fig. S1 D), which allows the activation gate to closely track changes in membrane potential.

Fig. 2 F shows the fast (u_i,f, solid black line) and slow (u_i,s, black dashed line) inactivation gating variables as a function of test potential, with the slow inactivation-gating variable V_0.5 marked by a teal dot. For membrane potentials positive to V_0.5 (teal dot), the slow inactivation gate starts to close whereas for membrane potentials negative to V_0.5, the inactivation gates are mostly open. Fig. 2 D shows the inactivation gate open probability (u_i,f × u_i,s) as a function of time at stimulation cycle lengths of 265 ms (red) and 750 ms (blue). The rate independence of u_i,f × u_i,s (Fig. 2 D, blue versus red) can be explained from the AP time course (Fig. 2 A) and u_i’s voltage dependence (Fig. 2 F). For the slow inactivation gate to close, the membrane potential needs to be positive to V_0.5 (−5 mV). For the fast inactivation variable, the voltage dependence is even more positive. However, the AP, both at cycle lengths of 265 and 750 ms, spends negligible time at potentials positive to the V_0.5 of either fast or slow inactivation (positive to the blue-dashed line in Fig. 2 E). Moreover, the inactivation time constants are >1 s (Fig. S1 B), at least two orders-of-magnitude longer than the time the membrane spends above V_0.5. Hence, because the membrane spends very little time positive to V_0.5 and the inactivation gate time constants are slow to close, the inactivation gating variables remain mostly in their open state (>0.93 fractional availability, Fig. 2 D) irrespective of activation frequency.

Rate-dependent effects of I_Kur block on AP properties and underlying mechanism

When I_Kur is blocked, the plateau voltage is raised and I_Kr is enhanced, counteracting the repolarization delays caused by I_Kur block (8). Consequently, to understand the rate-dependent AP changes caused by I_Kur block, it is essential to analyze the associated changes in I_Kr. Fig. 3 A shows the steady-state I_Kr activation-gate variable in the Courtemanche model as a function of test potential, with V_0.1 (−28 mV), V_0.5 (−14 mV), V_0.75 (−7 mV), and V_0.9 (0 mV) marked and transposed as dashed lines onto Fig. 3 B. Fig. 3, B–D, shows the AP, I_Kur, and I_Kr simulations obtained at a cycle length of 1000 ms under control conditions (blue) and with 75% I_Kur block (red). I_Kur block elevates the plateau potential, bringing the membrane potential positive to I_Kr’s V_0.5 (−14 mV; green dashed line in Fig. 3 B) for the duration of phase 2 of the AP, leading to a 136% increase in I_Kr, an acceleration in phase-3 repolarization and no net change in overall APD (Fig. 3 B; APD₋₆₀ control versus I_Kur block = 255 vs. 256 ms, respectively). Fig. 3, E–G, shows the AP, I_Kur, and I_Kr simulations at a cycle length of 250 ms under control conditions (blue) and with 75% I_Kur block (red). Because of the change in AP morphology at the short cycle length, I_Kur block-induced elevation of the plateau fails to keep the plateau potential in the I_Kr activation range (e.g., V_0.5 of −14 mV; green dashed line in Fig. 3 E), hence, there is little I_Kr recruitment (ratio of total I_Kr with I_Kur block versus control = 1.40), leading to APD prolongation (APD₋₆₀ under control versus I_Kur-block conditions of 199 and 209 ms, respectively). Therefore, despite the fact that I_Kur is smaller at rapid frequencies, the ability of I_Kur block to prolong APD is enhanced.

I_Kur block and AF termination

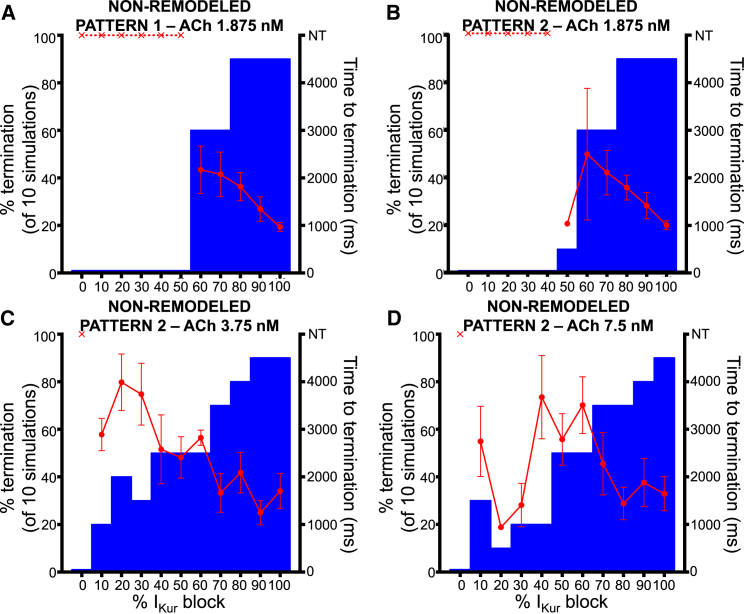
The above analysis suggests that the APD-prolonging effect of I_Kur blockade is preserved at rapid rates and might result in an ability to suppress AF. We therefore studied the effect of I_Kur block on simulated two-dimensional cholinergic AF. We generated nine ACh conditions (Fig. S4); reentry was sustained for >5 s across conditions but displayed markedly different dynamics ranging from single spiral wave reentry (Fig. S5) to multiple, short-lived wavelets (Figs. 4, S5, and S6 for representative examples). In line with our single-cell results, there were no significant differences in reentry dynamics, APD₋₆₀ distribution, and depolarized fraction between the original and modified I_Kur inactivation models (Figs. 5, S7, and S8 for representative examples). Using the non-remodeled Courtemanche human action potential model, we found a dose-dependent relationship between AF termination efficacy and percent I_Kur block (Fig. 6). Reentry termination was relatively infrequent with <50% I_Kur block, but increased to >90% of simulations at 100% I_Kur block for all conditions considered. We also found an inverse relationship between average time to termination and percent I_Kur block (Fig. 6).

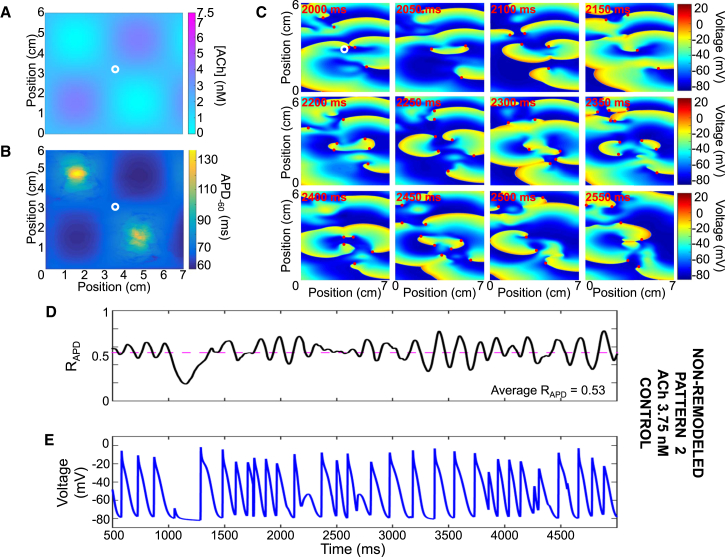
Figure 4.

Representative example of simulated vagotonic AF using pattern #2 with a peak ACh concentration of 3.75 nM and the non-remodeled cardiomyocyte model. (A) Shown here is ACh distribution with peak concentration of 3.75 nM and (B) a corresponding APD₋₆₀ distribution. (C) Shown here is transmembrane potential over time at 50-ms intervals; reentry is maintained by multiple short-lived spiral waves. (D) Shown here is the ratio of depolarized cells (ratio of cells with a voltage positive to −60 mV to the total number of cells) and (E) transmembrane potential over time for the cardiomyocyte marked with a white circle in (A) and (B).

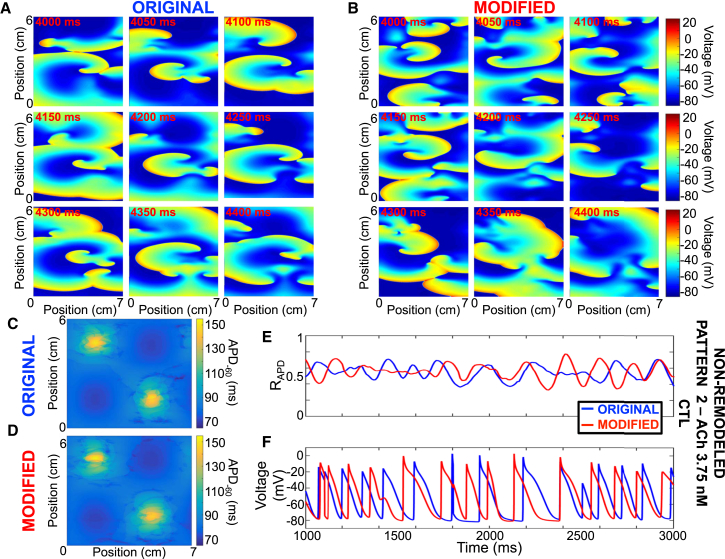
Figure 5.

Representative example comparing reentry dynamics in the original and modified models. (A and B) Transmembrane potential snapshots over time at 50-ms intervals for the original and modified models are shown. (C and D) APD₋₆₀ values for the original and modified models are given. (E and F) Shown here is the ratio of depolarized cells (ratio of cells with a voltage positive to −60 mV to the total number of cells) and transmembrane potential for the original (blue) and modified (red) models. Non-remodeled cardiomyocyte model with ACh pattern #2 with peak concentration of 3.75 nM is given.

Figure 6.

Dose-response (bar-graphs) and average time to termination (red data) by I_Kur block using the non-remodeled cardiomyocyte model for (A) ACh pattern #1 with peak ACh concentration of 1.875 nM. (B–D) Shown here are the ACh pattern #2 and peak ACh concentrations of 1.875, 3.75, and 7.5 nM, respectively.

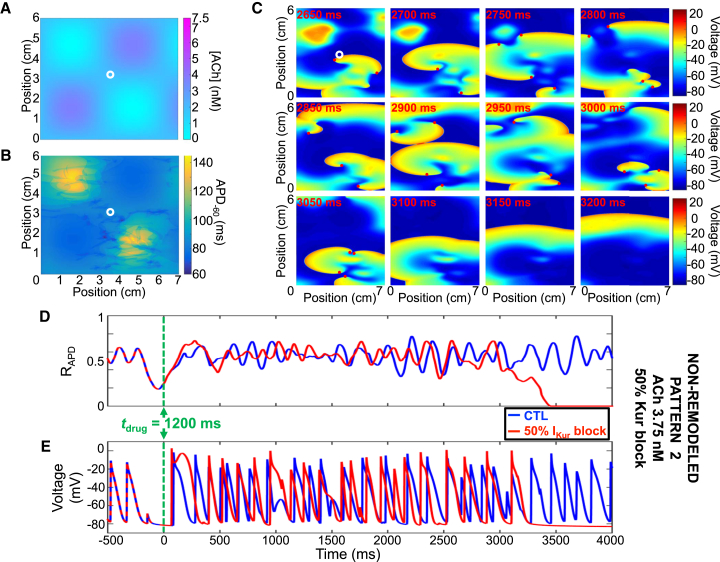
Fig. 7 shows a representative example of successful AF termination by 50% I_Kur block with ACh pattern #2 and a peak concentration of 3.75 nM (Fig. 7 A). The areas of largest ACh concentration had the shortest APs (Fig. 7 B). I_Kur block prolonged refractoriness, increasing the excursion of the phase singularities, favoring wave-front collision, annihilation, and reentry termination (Fig. 7, C–E). Fig. S9 shows the dynamics with the same ACh pattern/concentration but with 100% I_Kur block; the increased refractoriness is even more pronounced and termination more rapid. Consistent with a significant role of I_Kur in AP repolarization, the mean APD₋₆₀ increased from 85 ms under control conditions to 97 and 126 ms at 50 and 100% I_Kur block, respectively.

Figure 7.

Representative example of reentry termination by 50% I_Kur block using ACh pattern #2 with peak ACh concentration of 3.75 nM and the non-remodeled cardiomyocyte model. (A)Shown here is the ACh distribution with peak concentration of 3.75 nM and (B) its corresponding APD₋₆₀ distribution. (C) Transmembrane potential snapshots over time at 50 ms intervals are given; 50% I_Kur block was introduced at t_drug = 1200 ms. (D) Shown here is the ratio of depolarized cells (ratio of cells with a voltage positive to −60 mV to the total number of cells) and (E) transmembrane potential over time for the cardiomyocyte marked with a white circle in (A) and (B) for control (blue) and 50% I_Kur block (red).

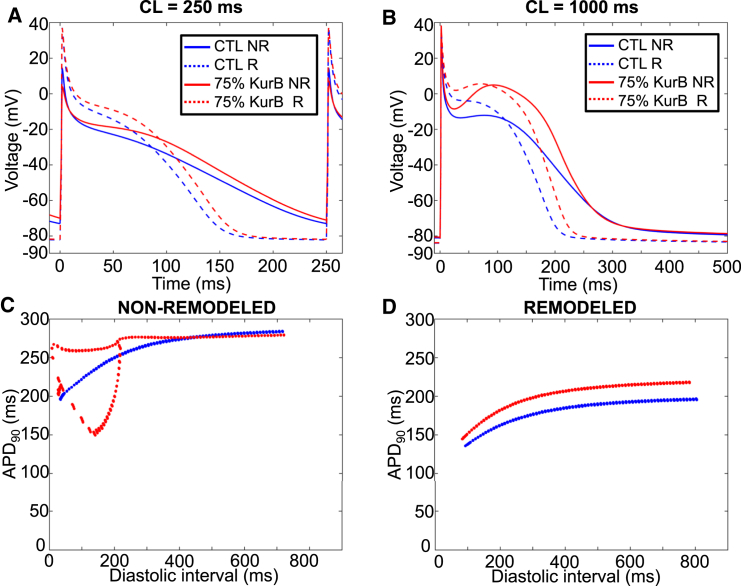
We then sought to investigate whether I_Kur block could successfully terminate two-dimensional AF under ionically remodeled conditions, such as in chronic AF. As previously reported (7), AF-remodeling conditions stabilize reentry dynamics (Figs. S10–S12) and ACh is no longer needed to maintain AF. Overall, the efficacy of I_Kur block in terminating AF in remodeled atria was very low, with no termination observed below 80% block and 10% termination at 90 and 100% block in the absence of ACh and across the nine ACh conditions (see Fig. S13 for a representative example). At the cellular level, remodeling stabilized reentry 1) by significantly shortening the APD₉₀ (APD₉₀ for non-remodeled versus remodeled was 283 vs. 195 ms, respectively at CL 1000 ms and 204 vs. 140 ms, respectively at CL 250 ms) and 2) by hyperpolarizing the resting membrane potential (RMP) as compared to the non-remodeled cardiomyocyte (Fig. 8, A and B, dashed versus solid) across a wide range of diastolic intervals. The I_Kur block-induced APD₉₀ prolongation was preserved under remodeled conditions (Fig. 8 C versus Fig. 8 D, red versus blue; ΔAPD₉₀ at CL = 250 ms non-remodeled versus remodeled was 11 vs. 10 ms, respectively). However, because the remodeled AP is of much shorter duration and is hyperpolarized, the diastolic interval is long enough for the AP to return to the RMP before the next activation, even at rapid stimulation frequencies (Fig. 8 A, blue versus red dashed). Conversely, for the non-remodeled cardiomyocyte, even a small prolongation in APD encroaches on repolarization at short CLs (Fig. 8 A, blue versus red solid), and I_Kur block causes APD alternans behavior at short CLs (Fig. 8 C). Hence, the differential efficacy of I_Kur blockade for AF termination in remodeled versus non-remodeled atria appears to be related to the remodeling-induced APD-abbreviation and hyperpolarization more than from I_Kur downregulation, because the APD prolongation caused by I_Kur block is preserved in remodeled cardiomyocytes.

Figure 8.

I_Kur blocking effects in remodeled cardiomyocytes. (A) Shown here is a single cell AP at a stimulation CL of 250 ms for a non-remodeled (NR; solid) and remodeled (R; dashed) cardiomyocyte without drug (blue) and with 75% I_Kur block (red); (B) same as in (A), but at CL of 1000 ms. (C) Shown here is an AP at 90% repolarization (APD₉₀) as a function of diastolic interval without drug (blue) and with 75% I_Kur block (red) for a non-remodeled cardiomyocyte; (D) same as in (C), but for a remodeled cardiomyocyte.

Discussion

In this study, we have developed an updated formulation of I_Kur inactivation kinetics that reproduces experimentally observed I_Kur inactivation properties. Using the model, we have shown that, under physiological stimulation conditions, I_Kur dynamics are mainly determined by its activation kinetics with relatively minor contribution from channel inactivation. Hence, 1) contrary to intuition, I_Kur inactivation does not accumulate at rapid stimulation frequencies; and 2) despite a rate-dependent decrease in absolute I_Kur magnitude, the relative contribution of I_Kur to AP repolarization increases with increased activation frequency. We also found that I_Kur block terminates simulated cholinergic AF in a dose-dependent fashion in non-remodeled atrial tissue but is ineffective in the presence of simulated atrial remodeling. Because I_Kur is expressed in the human atrium but not ventricle (9), it is an interesting potential candidate for atrial-selective anti-AF therapy. Therefore, the demonstration that despite its potential for complete inactivation, I_Kur maintains a significant contribution to repolarization dynamics and arrhythmia maintenance during AF, is potentially important.

I_Kur inactivation

The initial reports characterizing I_Kur inactivation used relatively short test pulses, typically <5 s long, and therefore failed to observe the full scale of I_Kur inactivation (1, 10, 11, 12, 13, 14). Using 50-s test pulses, Feng et al. (2) demonstrated that human atrial I_Kur inactivates fully, with a biexponential time-course characterized by rapid and slow time constants of 1.0 and 6.8 s, respectively. Moreover, I_Kur inactivation was found to be highly time-, voltage-, and frequency-dependent. These observations raised the possibility that channel inactivation could accumulate at rapid activation frequencies, significantly decreasing I_Kur’s contribution to AP dynamics. If I_Kur inactivated completely at rapid activation frequencies, such as during AF, then I_Kur blockers would be predicted to have minimal antiarrhythmic effects. Paradoxically, and contrary to this intuitive expectation, recent work with the highly selective I_Kur blocker XEN-D0103 found that I_Kur block prolongs the atrial APD and effective refractory period preferentially at rapid activation frequencies (3).

Novel elements relative to prior in silico work

To our knowledge, none of the commonly used human atrial in silico models correctly reproduces the experimentally observed I_Kur inactivation kinetics. In this investigation, we first analyzed experimental recordings of I_Kur inactivation to produce an accurate in silico representation. We then studied I_Kur inactivation dynamics and rate-dependence with the updated model that accounted realistically for I_Kur inactivation (2) by introducing a set of fast and slow inactivation gating variables (u_i,f and u_i,s) and corresponding time constants (τ_ui,f and τ_ui,s). The modified model accurately reproduced I_Kur time-, voltage-, and frequency-dependent inactivation across a wide range of physiological test potentials. Of note, the inactivation-gate time constants are three orders-of-magnitude slower than the activation-gate time constant (second versus millisecond). After including the updated I_Kur representation in the Courtemanche AP-model, we compared AP parameters as a function of stimulation cycle length and found no significant difference between the original and modified model results despite markedly different inactivation kinetics. We then applied our model to gain insight into the role of I_Kur activation and inactivation on I_Kur and its rate-dependent role in repolarization and arrhythmia maintenance.

Mechanism of I_Kur rate dependence

Using the modified model, we showed that the activation gate open probability is highly rate-dependent (because of rate-induced AP morphology changes) and parallels I_Kur rate dependence, whereas the inactivation gate open probability is effectively rate independent because the cell spends little time at voltages associated with significant inactivation-gate closure. Hence, I_Kur rate-dependence is due to its activation gating-variable dynamics and rate-dependent changes in AP morphology, with no contribution from inactivation.

Rate-dependent effect of I_Kur block on AP repolarization

We next sought to understand the mechanism underlying the positive rate-dependent effect of I_Kur block on the APD, as reported by Ford et al. (3). At slow stimulation frequencies, I_Kur block significantly elevated the AP plateau potential compared to control (no block), keeping the membrane at potentials for which I_Kr’s activation gate opens for the duration of phase 2 of the AP, leading to recruitment of I_Kr and compensating for I_Kur blockade with minimal effect on the APD. At rapid stimulation frequencies, the membrane potential is negative to I_Kr’s half-activation potential leading to little I_Kr recruitment, limited compensation by I_Kr, and I_Kur block-induced APD prolongation at rapid frequencies. Hence, although I_Kur’s absolute magnitude is less at rapid activation frequencies, the relative contribution of I_Kur to AP repolarization makes I_Kur block a potentially interesting atrial-selective anti-AF strategy.

The mechanisms of reverse rate-dependency (RRD) of drug-induced APD changes have been a matter of substantial debate. Arguing from first principles, Zaza (15) proposed that RRD is an intrinsic property of cardiac cells and that the same change in total transmembrane current will prolong long APs more than short ones. These predictions were supported by experimental work in which APD changes were shown to be proportional to the initial APD using clinically available drugs like the class-I agent lidocaine and class-III agent dofetilide, as well as by applying inward or outward current pulses (16). The same group suggested that channel blockers may, at best, attenuate this intrinsic RRD but that forward rate-dependency (FRD) would be “difficult to attain” (16). In an elegant study using a series of ventricular cardiomyocyte models, Cummins et al. (17) challenged this notion by suggesting that RRD can be overcome if rate-dependent AP morphological changes are large enough. In other words, the complex nonlinear rate-dependent changes in current dynamics may be such that RRD could be offset, making FRD possible. For example, they showed that increasing I_Ca,L (g_Ca,L) leads to FRD changes by elevating the AP plateau potential, leading to differential I_Ks activation at slow activation frequencies (17). Because I_Kur is not expressed in ventricular cardiomyocytes, the possible FRD properties of I_Kur block could not be evaluated. Our findings in atrial cardiomyocytes are, however, qualitatively in line with these observations, because we found that I_Kur block moves the AP plateau potential to more positive voltages, leading to differential I_Kr activation at slow versus rapid pacing rates and FRD APD-prolongation. Hence, FRD APD-prolongation, a highly desirable antiarrhythmic property, may be an attainable goal.

Relevance for antiarrhythmic drug development

We also found that I_Kur block terminates simulated cholinergic AF in a dose-dependent manner in nonionically remodeled atrial tissue by prolonging refractoriness, increasing the reentry wavelength, favoring rotor collision and annihilation. These findings are consistent with prior experimental work using relatively I_Kur-specific blockers in goats, rats, pigs, humans, and in silico systems (18, 19, 20, 21, 22). Electrical remodeling shortened the APD and hyperpolarized the RMP, leading to very stable reentry as described in Pandit et al. (7). The ability of I_Kur block to terminate simulated AF was greatly attenuated by remodeling, because the block-induced APD-prolongation was insufficient to counteract the strong effects of remodeling. The APD-prolonging effect of I_Kur block was not per se affected by channel downregulation. These observations are consistent with the report by Ford et al. (3), in which APD₉₀ prolongation induced by the I_Kur-selective blocker XEN-D0103 was maintained in chronic-AF human atrial cardiomyocytes. Scholz et al. (22) found that I_Kur block was effective at terminating simulated AF, even in remodeled atria. However, they used slightly different remodeling parameters, included gap junction remodeling, and did not incorporate I_Kur downregulation. The differential effectiveness of I_Kur block in non-remodeled versus remodeled atria is consistent with a prior randomized phase-3 clinical trial in which vernakalant, a mixed I_Na/I_Kur blocker, was much less effective at restoring sinus rhythm in patients with long-lasting AF (4.0%) compared to recent-onset AF (51.7%) (23). Of note, recent experimental work demonstrated persistent antiarrhythmic efficacy of vernakalant in goats with remodeled atria owing to unaltered effects on Na⁺-dependent parameters (conduction velocity and postrepolarization refractoriness) (24). Our findings suggest that the clinical efficacy of pure I_Kur block may be limited to recent-onset AF, in which remodeling has not taken place.

For the purposes of this study, I_Kur block was simulated as a fixed reduction in maximal conductance (g_Kur). However, there is in silico and experimental evidence that the electrophysiological and antiarrhythmic effects of I_Kur blockade are modulated by the time- and voltage-dependent kinetics of block. Using a family of I_Kur-selective diphenyl phosphine oxide compounds, Lagrutta et al. (25) were able to show that I_Kur blocking potency and frequency dependence were functions of blocking kinetics, with open state blockers being the most effective I_Kur antagonists. Several other molecules, including vernakalant and experimental compounds like zatebradine, loratadine, and bisindolylmaleimide, have also been shown to block I_Kur preferentially in the open state (19, 26, 27, 28). Mathematical simulations support these findings and suggest that I_Kur blockers with rapid binding or slow unbinding kinetics have the strongest antiarrhythmic effects (22, 29). Further work is needed to analyze the effects (if any) on state-dependent drug block, of adding realistic I_Kur inactivation kinetics.

Consistent with this study, XEN-D0101, a selective I_Kur blocker, prolonged the atrial effective refractory period (AERP) and decreased AF vulnerability in a dose- and rate-dependent manner in atrial tachycardia-induced remodeled canine atria (30, 31). In human cardiomyocytes, XEN-D0101 prolonged AERP in AF-remodeled but not in non-remodeled tissue (32). However, experiments were conducted using a stimulation frequency of 1 Hz at which we predict no effect on APD and AERP based on this study; rapid stimulation rates at which I_Kur-block induced prolongation of APD/atrial refractoriness would be expected were not reported. In coronary-perfused canine atria, 4-aminopyridine (a moderately selective I_Kur blocker) was found to shorten APD and to increase the propensity for AF, displaying only mildly antiarrhythmic effects in remodeled atrial tissue (33). Again, the protocol employed a stimulation cycle length of 500 ms at which I_Kur block would not be expected to increase the APD or AERP. Furthermore, the mechanism of I_Kur in dog atrium is different from that in humans, and the magnitude is often very small (34). MK-0448 failed to prolong AERP in healthy human subjects using relatively slow stimulation cycle lengths of 400 and 600 ms at which I_Kr recruitment balances I_Kur block (35). I_Kur block rate-dependence, as described in this study, along with species- and remodeling-related differences, likely account for these conflicting results. Finally, genetic studies reported both loss- and gain-of-function variants associated with the development of lone AF (36, 37, 38, 39). Whether and how these observations in rare genetically based forms of AF are applicable, remains to be seen more broadly.

Na⁺ channel blockers (NCBs) are moderately effective antiarrhythmic drugs commonly used to control AF (40). In 2015, it was reported that I_Kr block increases the anti-AF effects of an optimized NCB by delaying repolarization at rapid rates (41). However, I_Kr blockers have reverse-use-dependent effects on APD, such that the APD-prolonging effect of I_Kr block is maximal at the slow rates of normal sinus rhythm (producing a serious risk of excess repolarization delay and ventricular proarrhythmia) and decreases markedly at rapid rates like those of AF. Given the positive rate-dependence of the APD-prolonging effect of I_Kur block, the addition of an I_Kur blocker to an optimized NCB would be expected to potentiate the NCB’s anti-AF efficacy preferentially at rapid rates such as during AF. We have already shown evidence for this principle in a canine computational model (41). The work presented here provides tools and further rationale for testing this concept in human models.

Study limitations

First, this study was performed in silico with extensive use of prior primary experimental patch-clamp data (2). The model predictions regarding the rate-dependent effects of I_Kur block on AP properties need to be tested prospectively in human tissue. Second, the model does not consider I_Kur modulation by adrenergic (42) or by vagal (30) tone, nor by temperature dependence (2). However, the model was based on data obtained at normal body temperature and should therefore be relevant to normal clinical conditions. Finally, as discussed above, we simulated I_Kur block with a fixed reduction in maximal conductance, whereas I_Kur block by antiarrhythmic drugs have been shown to depend on blocking kinetics and show state-dependent properties (22, 29, 43). Further computational analyses considering the state-dependent actions of specific I_Kur blockers might therefore be of interest.

Our simulations in remodeled atria have one major limitation. To compare remodeled results with those in non-remodeled conditions, we used the same I_KACh model and distributions. However, I_KACh is greatly reduced in remodeled atria (44). There are no realistic I_KACh models for remodeled atria. Future work is needed to create such models and use them to obtain a more accurate picture of I_Kur-blocking effects under these conditions.

Conclusions

An updated in silico model that accounts for experimentally observed I_Kur inactivation kinetics shows that, contrary to possible intuitive inferences based on the potentially complete inactivation shown by I_Kur, I_Kur inactivation is in fact negligible under physiologically relevant conditions. On the contrary, the main determinant of I_Kur rate dependence is the response of its activation dynamics to frequency-dependent changes in AP-morphology. However, despite a smaller absolute I_Kur magnitude at rapid rates, the relative contribution of I_Kur to AP repolarization increases because of decreases in offsetting currents, particularly I_Kr. These positive rate-dependent effects allow I_Kur block to terminate AF and position it to have potentially valuable antiarrhythmic properties. At the same time, our results also suggest that the efficacy of I_Kur block for AF termination might be greatly attenuated in the ionically remodeled atrium that develops after several days or more of sustained AF (8).

Author Contributions

M.A. designed the study with the assistance of P.C. and S.N., performed all the simulations, analyzed the data and composed the manuscript. J.F. performed the original experimental work, provided all the original experimental data for analysis, and helped with the interpretation of the experimental results. E.V. provided the code for the AF simulation and assisted in its execution/analysis. P.C. supervised the modeling work and provided comments to improve the manuscript. S.N. supervised all aspects of the work, contributed to the original study concept and design, and helped with planning and completion of the manuscript.

Editor: Eric Sobie.