Spontaneous oscillatory contraction (SPOC) in cardiomyocytes

Abstract

SPOC (spontaneous oscillatory contraction) is a characteristic state of the contractile system of striated (skeletal and cardiac) muscle that exists between the states of relaxation and contraction. For example, Ca-SPOCs occur at physiological Ca²⁺ levels (pCa ∼6.0), whereas ADP-SPOC occurs in the virtual absence of Ca²⁺ (pCa ≥ 8; relaxing conditions in the presence of MgATP), but in the presence of inorganic phosphate (Pi) and a high concentration of MgADP. The concentration of Mg-ADP necessary for SPOC is nearly equal to or greater than the MgATP concentration for cardiac muscle and is several times higher for skeletal muscle. Thus, the cellular conditions for SPOC are broader in cardiac muscle than in skeletal muscle. During these SPOCs, each sarcomere in a myofibril undergoes length oscillation that has a saw-tooth waveform consisting of a rapid lengthening and a slow shortening phase. The lengthening phase of one half of a sarcomere is transmitted to the adjacent half of the sarcomere successively, forming a propagating wave (termed a SPOC wave). The SPOC waves are synchronized across the cardiomyocytes resulting in a visible wave of successive contractions and relaxations termed the SPOC wave. Experimentally, the SPOC period (and therefore the velocity of SPOC wave) is observed in demembranated cardiomyocytes and can be prepared from a wide range of animal hearts. These periods correlate well with the resting heartbeats of a wide range of mammals (rat, rabbit, dog, pig and cow). Preliminary experiments showed that the SPOC properties of human cardiomyocytes are similar to the heartbeat of a large dog or a pig. This correlation suggests that SPOCs may play a fundamental role in the heart. Here, we briefly summarize a range of SPOC parameters obtained experimentally, and relate them to a theoretical model to explain those characteristics. Finally, we discuss the possible significance of these SPOC properties in each and every heartbeat.

Introduction

The heart is an important internal organ whose role is to pump blood to all parts of the body via repeated contraction (shorten) and relaxation (lengthen) of its heart muscle cells, or cardiomyocytes. Man has a heart rate of about 70 beats per minute, roughly equivalent to 3 billion heartbeats in a lifetime. The human heart consists of four chambers, left and right atria, and left and right ventricles. The right chambers collect venous blood returning from the body and pumps it to the lungs under relatively low pressure. The left chambers receive oxygenated blood from the lungs and pumps it at relatively high pressure around the body.

Heart disease (ischaemic and hypertensive) is a major global burden with a high mortality (http://www.who.int/mediacentre/factsheets/fs310/en/). Heart failure reduces cardiac output that results in an inadequate supply of oxygenated blood to meet the metabolic demands of the body. One common form of heart failure is caused by dysfunction of the heart muscle, known as cardiomyopathy. It may be caused by mutations in sarcomeric or cytoskeletal genes, but in most cases the exact etiology remains unknown and are hence termed idiopathic.

The molecular mechanism by which muscle contraction occurs can be explained by the “sliding filament” theory. This theory proposed the sliding of actin and myosin filaments over each other such that the sarcomere shortens and thereby contracts (Huxley and Niedergerke 1954; Huxley and Hanson 1954; Huxley 1957). Ca²⁺ was later recognized as an essential regulator of muscle contraction. Ca²⁺ binds to troponin (Tn), a thin filament sarcomeric protein (Ebashi and Endo 1968; Ebashi et al. 1969), to enable the formation of active cross-bridges that thereby induces muscles to contract. Even under relaxing conditions, an ADP-bound head and a nucleotide-free rigor head can attach to and activate the thin filaments (Bremel and Weber 1972; Cooke and Pate 1985; Shimizu et al. 1992). These heads themselves do not produce active tension, but can allosterically activate the local area of the thin filaments. As a result, the attachment of myosin in an ADP-Pi state (pre-power stroke state) becomes possible and can enter into the force-generating state (Shimizu et al. 1992; Fukuda et al. 1998). Thus, both the ADP-head and the rigor head function as activators of the contractile system of muscle.

In this review, we will discuss the contractile system in cardiomyocytes as an autonomous machine that can undergo auto-oscillations (SPOCs). See published reviews on the properties of SPOC on skeletal muscle fibers and myofibrils: Ishiwata and Yasuda (1993), Wolfe et al. (2011), and Ishiwata et al. (2011).

Structure of cardiac muscle

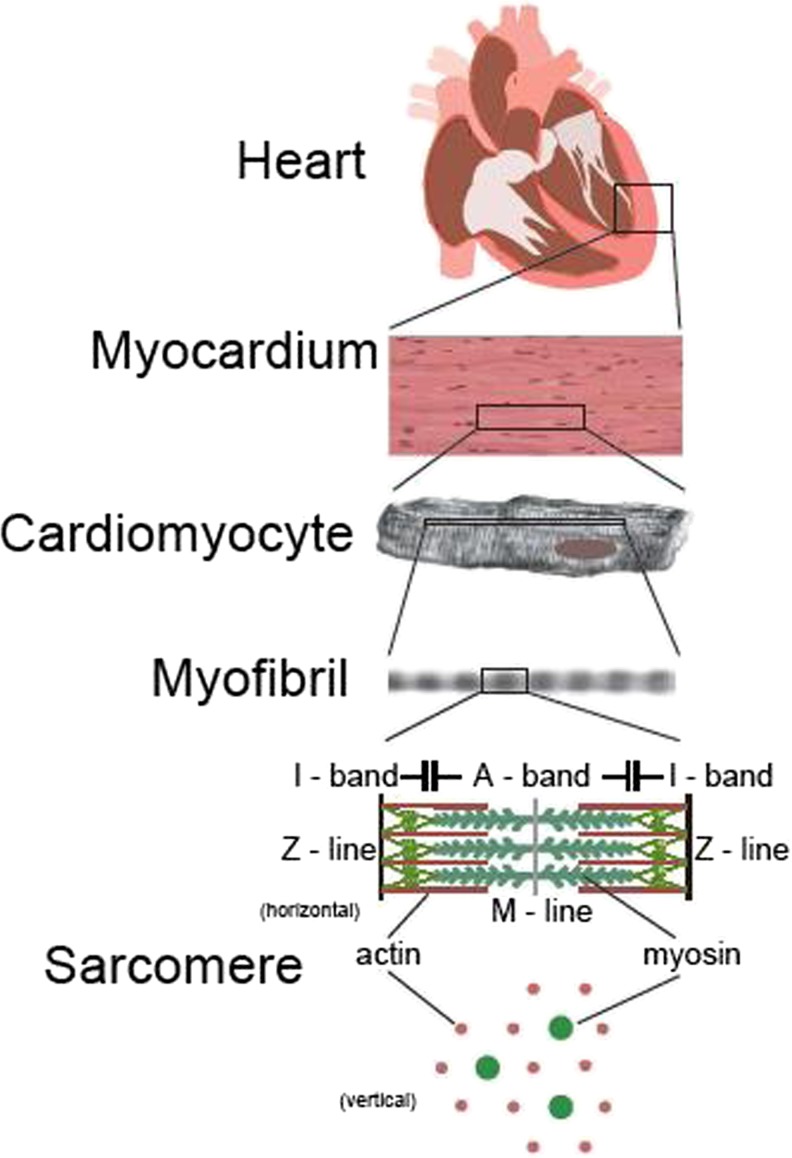
Striated muscle is structurally and functionally hierarchical as schematically illustrated in Fig. 1.

Fig. 1.

Hierarchical structure of heart. The myocardium, which is one of the walls of the heart, is an assembly of the cardiomyocytes. There are muscle fibers in the cardiomyocyte, and the muscle fiber is a bundle of myofibrils. A myofibril is constituted of sarcomeres that are connected in series. Shortening and lengthening of sarcomeres cause contraction and expansion of the heart

The heart as an organ

Cardiac muscle is structurally similar to skeletal muscle, and both are classified as a striated muscle. Cardiac muscle cells are mononucleated, unlike skeletal muscle which is a multinucleated cell. It has specialized gap junctions along its boundaries known as intercalated disks through which ions and small molecules are efficiently transferred between adjacent cells. In skeletal muscle, fibers (cells) are aligned almost in parallel to each other, and both ends are attached to bones through tendons, so that the generated force is transmitted to bones thereby generating movement. The force generated by the skeletal muscle is therefore balanced against a load. On the other hand, the wall of the myocardium is organized as two-dimensional sheets forming a multilayered bag-like structure. Thus, the three-dimensional structure of the heart is topologically quite different from that of skeletal muscle. Additionally, the ends of cardiomyocytes are not attached to bones. As such, the force generated by cardiomyocytes is balanced against the pressures required ejecting the blood from each chamber. Note that the heart is an involuntary organ, meaning that the heartbeat occurs autonomously.

The cardiomyocyte

Both cardiomyocytes and skeletal myocytes have T-tubules and an endoplasmic reticulum, or sarcoplasmic reticulum (SR) in the case of cardiomyocytes, to transmit the electrical signal and store Ca²⁺, respectively. These two membrane systems play an important role in the transmission of the contraction-relaxation signal. In contrast the concentration of mitochondria in cardiomyocytes is higher than skeletal myocytes as the heart requires a continuous supply of energy for ATP hydrolysis to beat continuously. Both cardiomyocytes and skeletal myocytes are composed of bundles of myofibrils about 1 μm in diameter. Intermediate filaments connect myofibrils to maintain the side-by-side positions of sarcomeres, so that the three-dimensional structure of a muscle cell has a smectic liquid crystalline structure with long-range striations. These myocytes are generally chemically demembranated, to enable the study of muscle physiology. In the case of SPOC, we usually use a glycerol and a detergent to remove the membrane of cardiomyocytes leaving an assemblage of the contractile proteins which we refer to as “the contractile system of muscle”.

The myofibril

A myofibril is a basic string-like unit of a muscle fiber that is comprised of a series of sarcomeres. Observation of myofibrils with an optical microscope, e.g., a phase contrast or a polarizing microscope, shows a periodic structure (∼2 μm long) along the long axis of a myofibril. Cardiac myofibrils, unlike its skeletal counterpart, have shorter I bands (see below). While the shortening velocity of each myofibril is nearly proportional to the number of sarcomeres, its force generation is independent of this number. We are able to examine the contractile properties of cardiac myofibrils (even from human preparations) without a membrane system using the same microscopic technique developed for studying sarcomere dynamics in skeletal myofibrils (Anazawa et al. 1992; Shimamoto et al. 2009).

The sarcomere

The sarcomere is the structural and functional unit of a myofibril. It is mainly composed of three kinds of myofilaments termed the thin filaments, thick filaments and titin (or connectin) filaments (Maruyama et al. 1976; Wang et al. 1984). Filamentous actin, a helical polymer of actin monomers (∼42 kDa), forms the core of each thin filament that is then surrounded by the tropomyosin (Tm) and Tn regulatory proteins. Troponin I (TnI) and T (TnT) interact periodically with actin and Tm to inhibit myosin binding, while troponin C (TnC) binds Ca²⁺ to release these inhibitions thereby enabling cross-bridge formation with myosin. Myosin II (∼500 kDa) is the molecular motor that makes up the backbone of thick filaments. Myosin alone accounts for ∼60 % of the total protein in the contractile system of striated muscle. The gigantic connectin/titin protein, a known binding partner of myosin and actin, constitutes the third filament that has its N-terminus at the Z-line and its C-terminus inserted into the M-line. Cardiac and skeletal muscles express their respective contractile protein isoforms despite its similar mechanism of action.

Thick filaments have a bipolar structure centered about the sarcomere midline or the M-line. It interacts with the thin filaments that extend towards, but generally do not reach, the M-line. The extent of overlap between the thick and thin filaments decreases with extension of the sarcomere. One end of the thin filament attaches to the Z-line where it becomes cross-linked by α-actinin to stabilize the thin filaments. The Z-line contains many other proteins, and together they stabilize the Z-line structure. Figure 1 shows a cross-section of the A-band, with both myofilaments forming a hexagonal lattice structure.

Function of cardiac muscle

Contraction of cardiac muscle is regulated by both endogenous and exogenous mechanisms. The Frank–Starling law of the heart is an endogenous mechanism (Bers 2001) and is widely considered to be equivalent to the length-dependent activation in the contractile system of cardiac muscle (Terui et al. 2008, 2010). Recently, the involvement of TnT in the relationship between this mechanism and heart disease has been found: a mouse model of dilated cardiomyopathy with mutated TnT showed depressed Frank–Starling mechanism in the left ventricular muscle (Inoue et al. 2013; Kobirumaki-Shimozawa et al. 2014). An exogenous mechanism is attributed to the actions of hormones in blood, the autonomic nervous system, ion concentration, metabolites, and so on.

Each beat of the heart involves cycles of contraction and relaxation of the sarcomeres that are precisely controlled by changes in intracellular Ca²⁺ level. Intracellular Ca²⁺ in the myocardium can be enhanced by an influx of Ca²⁺ through the L type Ca²⁺channel located at cell membrane. It initiates Ca²⁺ release from the SR, and subsequently increases the Ca²⁺ gradient by the cooperative release of Ca²⁺ by a calcium-induced Ca²⁺ release (CICR) mechanism. Conversely, the decrease in intracellular Ca²⁺ concentration is achieved by exporting it to the extracellular space via the Ca²⁺ pump or the Na⁺–Ca²⁺ exchange mechanism at the cell membrane, and by uptake into the SR by Ca²⁺ pump (SERCA). See Walweel et al. in this special issue for detailed explanation of SR calcium release.

As the intracellular concentration of Ca²⁺ increases to ∼1 μM, Ca²⁺ binds to TnC. This then shifts the conformation of Tn-Tm into the grooves of the thin filaments, such that the interaction between actin and myosin becomes possible. Thus, the contraction and relaxation cycle is regulated by the cyclic changes in Ca²⁺ concentrations. Notably, the maximum concentration of Ca²⁺ in cardiomyocytes (pCa, ∼6.0) is not as high as in skeletal muscle (pCa, ≤5.0). This indicates that cardiac muscle, in contrast to skeletal muscle, is not fully activated. This difference is the result of activation type where the Ca²⁺ concentration is transiently increased due to the prolonged action potential in cardiac muscle, whereas the activation with repetitive action potentials with high frequencies in skeletal muscle causes tetanus due to superposition and fusion of repetitive force generation.

The responsiveness of cardiomyocytes to Ca²⁺ depends on sarcomere length (SL), the spatial relationship of actin and myosin, and the number of cross-bridges (Fuchs and Wang 1996). Extension of SL shifts the pCa-tension relationship to the left, i.e., an increase in the Ca²⁺ sensitivity of the contractile proteins upon extension of SL. pCa₅₀ is the value of −log[Ca²⁺] at which half of the maximum tension is developed. The molecular mechanism for the increase in the Ca²⁺-binding affinity to TnC upon stretching of muscle is not understood. It had been previously reported that Ca²⁺ sensitivity is reduced with lowering pH value (Fukuda and Ishiwata 1999), and also with increasing Pi concentration (Terui et al. 2010). These results suggest that the decrease in the number of force-generating cross–bridges decreases the Ca²⁺ sensitivity of TnC. This is consistent with the reduced Ca²⁺ sensitivity of the myocardium often observed during ischemia, in which the Pi concentration increases and pH is lowered.

As described above, both ends of cardiomyocytes are not fixed to a rigid body. Skeletal muscle frequently functions under isometric conditions, generating force at a fixed length. By contrast, cardiomyocytes mostly function under auxotonic conditions in which both total length and force change to maintain the balance with the blood pressure. This means that myofibrils and sarcomeres repeat shortening and lengthening without a pause under a normal condition. There is a consensus that these oscillations are induced by repetitive changes in Ca²⁺ concentrations. Thus, the contractile system of muscle is considered to be a simple working machine, i.e., a molecular device working under the control of electrical and chemical signals.

SPOC: spontaneous oscillatory contraction

Defining SPOC

SPOC is an auto-oscillatory phenomenon observed in the contractile system of striated muscles. A similar auto-oscillatory state is expected to exist in the contractile system of smooth muscle performing peristalsis but has not yet been examined. Each sarcomere oscillates with a saw-tooth waveform that consists of a fast lengthening and slow shortening phase while maintaining a constant periodicity. The lengthening phase in one-half of a sarcomere propagates to the adjacent half sarcomere in succession along the myofibril and is known as the SPOC wave.

The history of SPOC

In 1988, we reported that SPOCs occur under non-physiological conditions in skeletal muscle fibers, i.e., where the concentration of MgADP is higher than the MgATP concentration with several mM of Pi but essentially no free Ca²⁺ (Okamura and Ishiwata 1988). We later named this phenomenon ADP-SPOC. A similar auto-oscillation phenomenon was reported by Fabiato and Fabiato (1978) for cardiac muscle, under a rather more physiological condition, i.e., Ca²⁺ concentration that was intermediate between contraction and relaxation in the presence of Mg-ATP, but without the addition of ADP and Pi. We coined this auto-oscillation phenomenon as Ca-SPOC (Ishiwata and Yasuda 1993; Ishiwata et al. 2011). Fukuda et al. (1996) examined the reaction conditions for SPOC using various concentrations of MgADP, Pi and Ca²⁺ at a fixed concentration of MgATP, and at a fixed pH and temperature. Based on this and the subsequent studies, we constructed a three-dimensional state diagram of the contractile system of muscle consisting of contraction, relaxation and SPOC states (Ishiwata and Yasuda 1993; Ishiwata et al. 2011). This diagram clearly showed that the SPOC region constitutes a single large region sandwiched between the contraction and relaxation regions. The ADP-SPOC and the Ca-SPOC regions, respectively, are located at either end of the single SPOC region. However, it should be stressed that they belong to the same SPOC region. This strongly suggests that the molecular mechanisms of ADP-SPOC and Ca-SPOC are common, even though the apparent conditions for SPOC are quite different. Here, a brief history of SPOC research on cardiac muscle and theoretical work is summarized in Table 1.

Table 1.

Brief history of SPOC research: cardiac muscle and theoretical work

Exp. (muscle type) or theoretical	Conditions	References
Cardiac, g.mfa	pCa, 6	Fabiato and Fabiato (1978)
Cardiac, g.bb	pCa, 6	Brenner (1979)
Cardiac, g.b	pCa, 6	Sweitzer and Moss (1990)
Cardiac, g.mf	pCa, 6	Linke et al. (1993)
Cardiac, g.b	MgADP, Pi (±Ca)	Fukuda et al. (1996)
Cardiac reconstituted g.bc	MgADP, Pi, BDM	Fujita and Ishiwata (1998)
Cardiac, g.b	MgADP, Pi (±Ca)	Fukuda and Ishiwata (1999)
Cardiac, g.b	MgADP, Pi (−Ca)	Sasaki et al. (2005)
Cardiac, g.b	pCa, ≦6	Sasaki et al. (2006)
Cardiac, g.b	pCa, 6	Stehle et al. (2002)
Theor. (abstract)		Jülicher and Prost (1997)
Theor. (abstract)		Vilfan and Duke (2003)
Theor. (unit model)		Günther and Kruse (2007)
Theor. (unit model)		Smith and Stephenson (2009)
Theor. (unit model)		Sato et al. (2011)
Theor. (connected model)		Sato et al. (2013)

^a g.mf single and a small bundle of glycerinated myofibril

^b g.b glycerinated bundle of myofibers

^creconstituted glycerinated bundle of which the thin filaments were removed by treatment with gelsolin and then reconstituted using rabbit skeletal monomeric actin (Fujita et al. 1996)

Modeling the mechanism of SPOC

We recently constructed a unit model to explain the oscillation of SL of each sarcomere (Sato et al. 2011). Later, this was extended to a connected model that was developed to explain various patterns of SPOC wave observed in a myofibril in addition to SL oscillations (Sato et al. 2013). The unit model consists of three ordinary differential equations on the following three time (t)-dependent variables: the proportion of cross-bridges (myosin heads attached to actin), P(t); the length of overlap between the thick and the thin filaments, ξ(t) (equivalent to SL); and the distance between the thick and the thin filaments, i.e., the lattice constant, d(t).

The distinguishing characteristics of this model are: (1) the probability of cross-bridge formation depends on the lattice constant; and (2) the forces acting in the direction of width of the myofibril, which are originated from the elasticity, i.e., the spring constants, of cross-bridges and the filament lattice, are balanced. The unit model could reproduce almost all the properties of sarcomeric SPOC; namely, a saw-tooth waveform of SL oscillation and the phase diagram on the state of sarcomeres where the SPOC region is located between the contraction and relaxation regions.

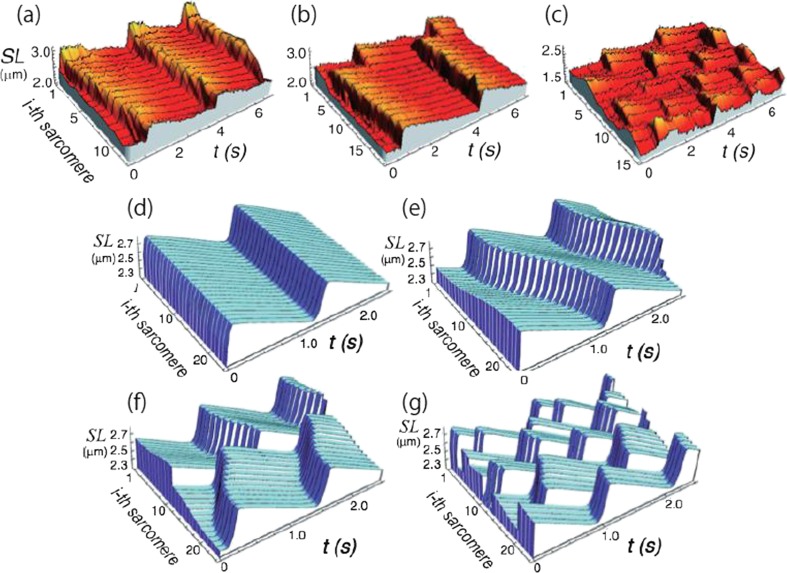
The connected model consists of the same three ordinary differential equations as the unit model, but additionally, the unit model is visco-elastically connected with the adjacent units (the local coupling), which simulates the structure of a myofibril. Furthermore, we assumed that each unit (sarcomere) experiences the same external force (load) at every moment (the global coupling), because the inertia (mass) of sarcomeres is negligibly small compared with the active force produced by the sarcomere. As a result, this connected model has succeeded in reproducing the characteristics of SPOCs observed in myofibrils, i.e., various kinds of SPOC waves. These include a metachronal SPOC wave, a disrupted SPOC wave propagating along a myofibril, an out-of-phase SPOC, and a synchronous SPOC. The model also presents a phase-diagram that consists of the regions of contraction (without auto-oscillation), an out-of-phase SPOC, a disrupted SPOC wave, a metachronal SPOC, and asynchronous SPOC (Fig. 2).

Fig. 2.

Examples showing typical spatiotemporal patterns of SL oscillations. a–c Representative patterns of SPOC obtained by the experiments on skeletal myofibrils (taken from Sato et al. 2013; see movies shown in the Supplemental Materials). a Traveling waves; b disrupted traveling waves; c out-of-phase synchronization. d–g Results obtained by a connected model for SPOC (taken from Sato et al. 2013). d In-phase synchronization; e traveling waves; f disrupted traveling waves; g out-of-phase synchronization

A qualitative explanation on the mechanism of SPOC

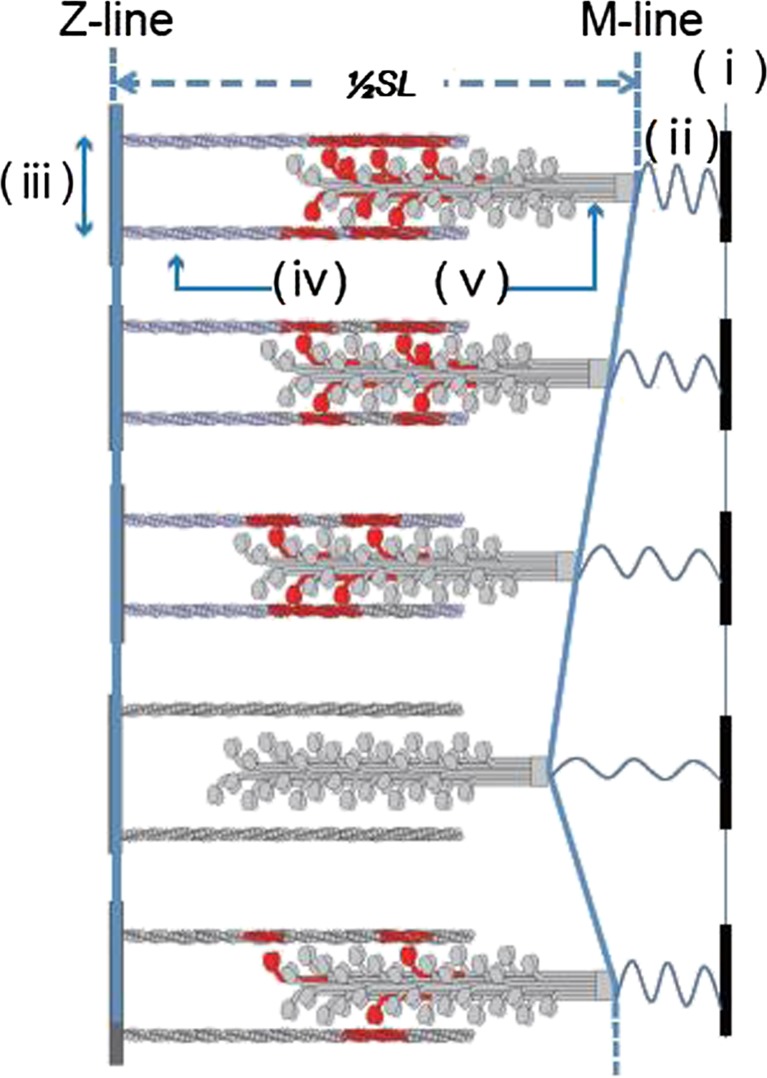
Figure 3 shows that the length of overlap between the thick and thin filaments increases as the sarcomere shortens such that the number of cross-bridges is expected to increase almost linearly. However, the system becomes unstable because of the increase in the separation between the two myofilaments to maintain a constant lattice volume, so that the probability of cross-bridge formation nonlinearly decreases. And, finally, at some shortened SL, the cross-bridges become unable to sustain the expanding filament lattice (note that the number of cross-bridges is not large because of the partial activation conditions). This results in the detachment of cross-bridges allowing the sarcomere to lengthen. The increase in SL gradually reduces the filament lattice that nonlinearly enhances the probability of cross-bridge formation despite the decrease in the overlapping region between the myofilaments. Consequently, elongation of the sarcomere stops at some SL due to the increase in the probability of cross-bridge formation allowing shortening to start again. This forms a cycle of slow shortening and rapid lengthening in SPOC.

Fig. 3.

Schematic illustration showing the cycle of sarcomeric oscillation in our SPOC model. Each sarcomere is slowly shortened (top). As the sarcomere is shortened, a myofilament lattice (iii), a distance between the thin (iv) and the thick (v) filaments, gradually tends to expand, so that the state of sarcomere becomes unstable. At some sarcomere length (SL; here only half a sarcomere is illustrated), the balance between the elastic forces due to the myofilament lattice and the cross-bridges is broken, resulting in the detachment of cross-bridges and the elongation of sarcomere. As the sarcomere is elongated, the myofilament lattice tends to shrink, so that the probability of cross-bridge formation is non-linearly increased and the elongation of sarcomere stops at some SL because of the cross-bridge formation. Under the auxotonic condition as illustrated here, where both SL and the applied external force (due to the extension of spring (ii) which is fixed at a rigid body (i)) change. As shown here, the change of SL shows a saw-tooth waveform, consisting of slow shortening and rapid lengthening

Such a cyclic motion is possible only under conditions of partial activation in which a portion of myosin heads forms cross-bridges. Under the full activation condition, almost all available myosin heads are able to form cross-bridges, so that their number is sufficient to keep the system stable even at a short SL. As a result, the sarcomere becomes shorter up to a sarcomere length where the oscillations are either dampened or ceases completely.

The important characteristics of SPOC

Here, we make several comments on the characteristics of SPOC, which are worth mentioning.

1. The elasticity of titin/connectin (Funatsu et al. 1990, 1993; Fukuda et al. 2001, 2008) is not essential for the mechanism of SPOC. The experimental evidence shows that the oscillation pattern of SPOC is not influenced by partial digestion of titin/connectin with chymotrypsin (Ishiwata et al. 1996). Also, SPOC occurs even at short sarcomeres at which the titin/connectin filaments are not stretched. However, it is probable that the elasticity of titin/connectin does modulate the SPOC pattern as modeled by Smith and Stephenson (2009).

2. The SPOC model we proposed (Sato et al. 2011, 2013) consists of three linear normal differential equations. We did not need to explicitly take into account the cooperativity of cross-bridge formation. However, there is a possibility that a more detailed mechanism will be required to explain the finer properties of SPOC. For example, the effects of temperature on the SPOC patterns are not considered in the present model.

3. The experimental evidence suggests that the average tension developed during SPOC is low (Endo 1972a, b; Shimamoto et al. 2007, 2008). However, it is highly probable that this is because the sarcomere oscillations are out-of-phase (at random). When the sarcomere oscillations are synchronized (ordered), the tension level is not necessarily low but intermediate.

4. The SPOC patterns are sensitive to external mechanical conditions, e.g., the spontaneous oscillations of sarcomeres that are not synchronized can become synchronized when an external mechanical impulse is applied (unpublished results: partly reported in Shimamoto et al. 2009), and the oscillations of sarcomeres are synchronized when the external load is maintained constant and only length oscillations are allowed, i.e., under isotonic conditions (Yasuda et al. 1996).

SPOC characteristics and myocardial oscillation

Is there a possibility that the characteristics of SPOC play a role in the function of heartbeat? The answer is likely yes. Ca-SPOCs are a good candidate as these can occur under physiological conditions where ADP levels are low, while the involvement of ADP-SPOC is unlikely given that there is little evidence that ADP levels rise above the normal ATP level. However, in heart failure, the concentration of ADP is elevated and the pH is lowered, so that the conditions for high levels of MgADP may be fulfilled in vivo (Fukuda and Ishiwata 1999). In practice, in cardiac muscle, the SPOC region is very broad as shown in the 3D phase diagram (Ishiwata and Yasuda 1993; Ishiwata et al. 2011).

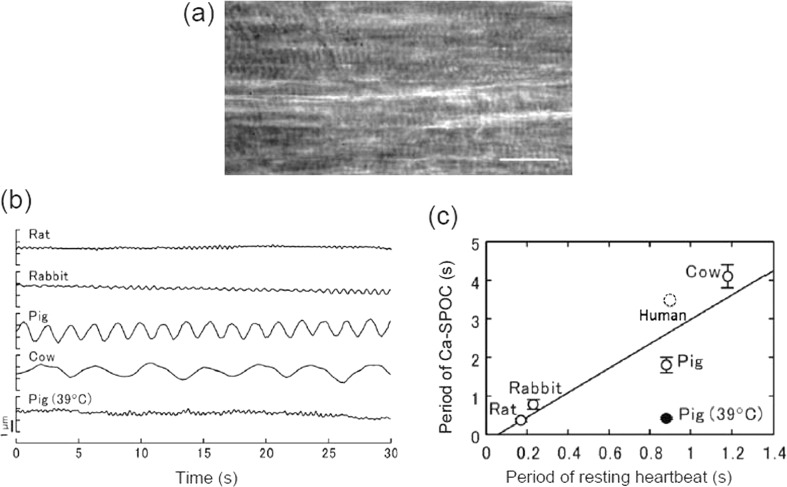
We found a strong correlation between the resting heartbeat in live animals and the oscillation periods of ADP-SPOC (Sasaki et al. 2005) and Ca-SPOC (Sasaki et al. 2006). Figure 4 illustrates a preliminary result obtained for human cardiomyocytes. These data obtained using glycerinated cardiomyocytes can be compared with data from the hearts of cows, pigs, dogs, rabbits and rats. Here, ADP-SPOC and Ca-SPOC were observed at room temperature.

Fig. 4.

Relationship between Ca-SPOC and heartbeat in various kinds of cardiomyocytes. a Phase-contrast microscopic image of human skinned cardiomyocyte. This sample was prepared by thawing the specimen kept in liquid N₂. Scale bar 20 μm. b Time course of the translational movement of a plastic bead (∼1 μm in diameter) attached on the surface of cardiomyocytes in Ca-SPOC. All the observations were carried out at 22 ± 1 °C except for porcine myocardium, in which the observations were also carried out at 39 ± 1 °C. c Relationship between the period of Ca-SPOC and the period of resting heartbeat. Open and closed circles, the period of Ca-SPOC at 22 ± 1 and 39 ± 1 °C, respectively. Vertical bars SD of five experiments. The solid line is the regression line for the period of Ca-SPOC at 22 ± 1 °C (correlation coefficient, 0.938). Taken from fig. 4 of Sasaki et al. (2006). A preliminary result showed that the relationship between the SPOC period and the heartbeat period of human cardiomyocyte is located near the dotted circle

The difference in SPOC rates can be explained by differences in myosin ATPase activity. The in vitro motility assay showed that the sliding velocity of actin filaments depended on the myosins prepared from different animal hearts, i.e., in the order of rat, rabbit, dog, pig and cow (Sasaki et al. 2005). These differences among animal species can be mainly explained by the expression of different ratios of cardiac myosin heavy chain (MHC) isoforms. Mammalian heart expresses two types of isoforms of MHC, α-MHC and β-MHC, resulting in three different types of myosin isoforms, V1 (αα), V2 (αβ) and V3 (ββ). All mammalian species express different ratios of their MHCs. For example, V1 (αα) is expressed in animals such as mice and rats where sliding velocities are fastest. On the other hand, V3 (ββ) is expressed in larger mammals such as man where the sliding velocity of V3 (ββ) is slower than that of smaller mammals. Thus, we conclude that the SPOC periods correlate well with filament sliding velocities of myosin isoform enzymatic activity (Barany 1967).

A possible role of SPOC in human heartbeat

As mentioned above, there is a strong correlation between the resting heart rate and the SPOC period of sarcomeres (Fig. 4). Resting heart rate is correlated with the sarcomere shortening velocity characteristic of each animal, which is attributable to the enzymatic activity of myosin motors (Barany 1967; Sasaki et al. 2005). SPOCs can synchronize with externally applied mechanical impulses (unpublished data). Moreover, sarcomeric auto-oscillation is tunable not only by external mechanical influences but also by oscillations in intracellular Ca²⁺ concentrations (unpublished data). These results imply that the SPOC properties inherent to the contractile system of cardiomyocytes are a fundamental property of the heartbeat.

The resting heart rate is controlled by the pacemaker in vivo, not the contractile system of cardiac muscle. However, it may be possible to state that, since the muscle cells must catch up with the rate created by the pacemaker, the contractile property, which is explicitly expressed in SPOC, cannot be independent of the heart rate.

How can we examine this possibility? We currently have no clear answer to this question. However, we have recently developed new techniques to visualize and quantify changes in sarcomere length in beating in live cardiomyocytes (Serizawa et al. 2011; Kobirumaki-Shimozawa et al. 2012; Shintani et al. 2014). Accordingly, we expect to also examine SPOCs during heartbeat in the near future.

In the case of human cardiac muscle, resting heart rate is about 70 per minute, which is similar to that of porcine. In addition, the volumes of human and porcine hearts are similar. Thus, human cardiac SPOC period is expected to be comparable to that of pig. But, in practice, the SPOC period of human myocardium appears to be longer (see Fig. 4) because the actin filament sliding velocity over human MHC is slower than that of pig (Malmqvist et al. 2004). The difference in myosin isoforms amongst animals is dependent on the size and shape of the animals that dictate blood pressure and/or the transportation of nutrition around the body.

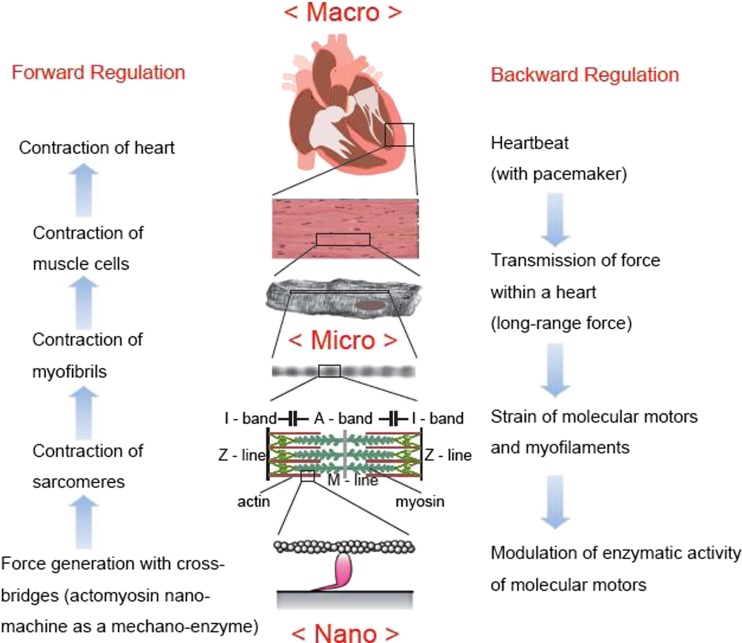
Efficient systemic circulation requires a rapid transition from the relaxing to the contracting state. In other words, staying at an intermediate state such as SPOC, rather than at the two extreme stable states (contraction and relaxation), may facilitate a quick transition. Generally speaking, the transition between the two states can more easily be controlled with an intermediate state. In this sense, the SPOC properties may be useful for underlying the efficient heartbeat. Finally, we would like to suggest that the heart is an organ in which macro- and nano-operations are directly coupled as described in Fig. 5. The heart is a motile apparatus that beats autonomously without rest. During each beat, force generated is quickly transferred to the whole body, and to the system (myocardium, cardiomyocyte, myofibril, sarcomere, myofilaments and molecular motors). Each level of the hierarchy will sense the force and modulate their functions according to their respective characteristics and responsibilities. Here, we assume there are forward and backward regulation pathways, forming a regulation loop characteristic of an autonomous system.

Fig. 5.

Schematic illustration explaining that the heart is an organ in which macro- and nano-operations are directly coupled through the long-range force produced by an assembly of molecular motors. At a nanoscopic level, an actomyosin motor, a stochastic nano-machine, produces a sliding force at random. In a sarcomere, an assembly of myofilaments, i.e., a bundle of the thick and the thin filaments, slides past to each other, resulting in the shortening of myofibrils, a series connection of sarcomeres, against the force (load) externally applied. As a result, cardiomyocytes, an assembly of myofibrils, and myocardium (Fig. 1), an assembly of cardiomyocytes, contract. Rhythmic contraction of heart occurs due to the coordinated contraction and relaxation cycle of myocardium constructing the heart outer and inner walls. Focusing on the force generation pathway, we call this “a feedforward regulation”. On the other hand, “a feedback regulation” pathway exists, i.e., the timing of heartbeat is controlled by electric impulse produced by pacemaker cells in a sinoatrial node. This signal is transferred to the myocardium through a conducting system. When cardiomyocytes at some region of heart begin to contract, those at the other region of heart will receive the stress due to the long-range force, resulting in the distortion of myofilaments and cross-bridges. This may cause the modulation of enzymatic activity of actomyosin motors and their regulation. Thus, we propose that a feedforward and feedback regulatory mechanism exists in heartbeat. In other words, there exists a chemo-mechanical feedback loop in the heartbeat. It means that heart is an organ in which macro- and nano-operations are directly coupled to each other

Conclusions

In conclusion, the assembly of molecular motors and cytoskeletons is intrinsically an auto-oscillator (Ishiwata et al. 2010, 2011). We expect that the SPOC properties inherent to the contractile system of muscle play an important part in heartbeat, and a study on SPOC is useful for characterizing normal and failing human cardiomyocytes.