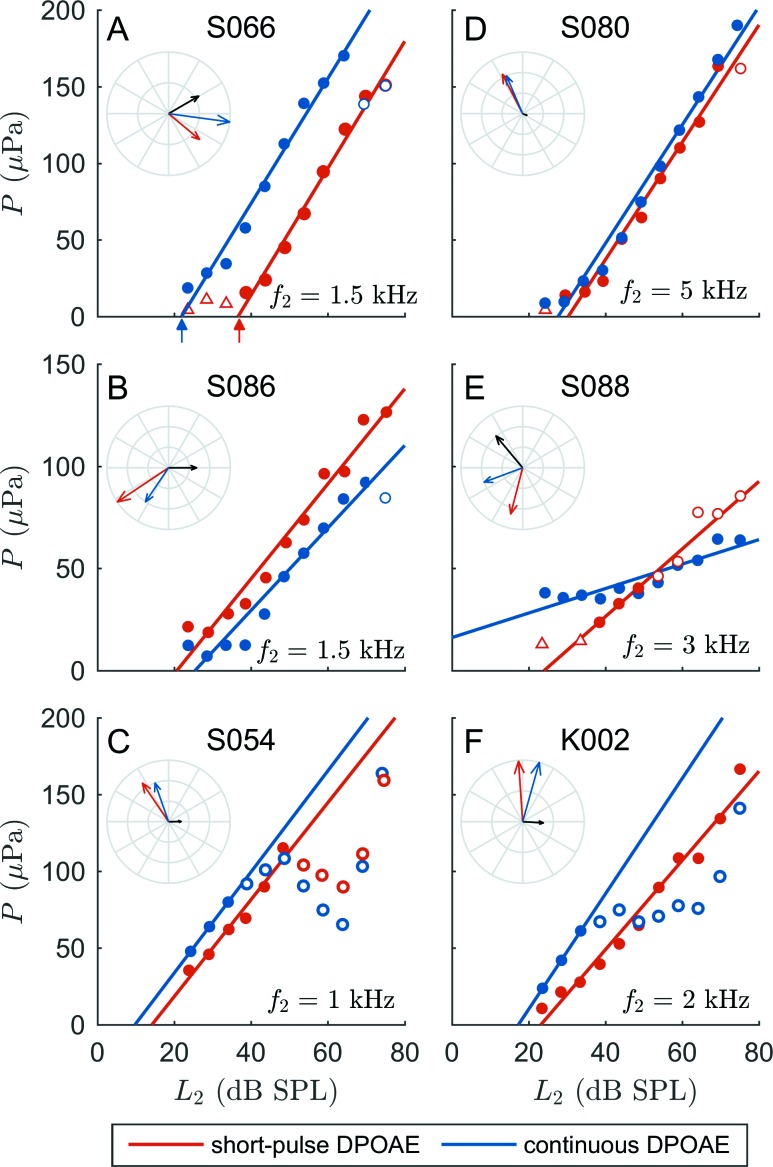
FIG. 5.

DPOAE I/O functions based on continuous (blue dots) and short-pulse (red dots) stimulation for six subjects. The intersections of the linear regression lines (blue and red lines) with the abscissa define the EDPTs (exemplarily indicated by the blue and red arrows in A). Empty triangles correspond to DPOAEs not complying with the 10-dB SNR criterion (Sec. II D), while empty circles depict data points excluded from the regression analysis by high-level correction (HLC; Sec. II E). Insets show diagrams of the phasors $P_1$ and $P_2$ (both rotating at 2πf_DP rad/s) of the nonlinear-distortion (red arrows) and coherent-reflection (black arrows) components extracted with PBF decomposition at L₂ = 45 dB SPL (Zelle et al., 2013; Zelle et al., 2015b), as well as the phasor sum $P_c=P_1+P_2$ (blue arrow), which provides an estimate of the continuous DPOAE phasor and serves as a comparison with the measured continuous DPOAE. The short-pulse DPOAE signals together with the statistical parameters associated with the PBF decomposition are given in the supplementary material.¹ The phasor amplitudes of $P_1$ and $P_2$ in A, B, E, and F indicate pronounced coherent-reflection components capable of altering I/O functions depending on the phase difference between $P_1$ and $P_2$. The coherent-reflection component in A enhances the amplitude of $P_c$, shifting the I/O function toward lower L₂ levels. In contrast, in B, destructive interference shifts the continuous I/O function toward higher L₂ values. In E and F, interference conditions vary considerably with stimulus level yielding an unreasonably flat I/O function in E and considerable deformations in F. Data in C and D do not contain references to pronounced coherent-reflection components. However, C depicts deformations in both I/O functions; these data points (empty circles) were detected by the HLC algorithm as being systematic deviations from the straight-line growth evident at low intensities and were, therefore, excluded from the regression analysis.