Noise and Epigenetic Inheritance of Single-Cell Division Times Influence Population Fitness

Summary

The fitness effect of biological noise remains unclear. For example, even within clonal microbial populations, individual cells grow at different speeds. Although it is known that the individuals’ mean growth speed can affect population-level fitness, it is unclear how or whether growth speed heterogeneity itself is subject to natural selection. Here, we show that noisy single-cell division times can significantly affect population-level growth rate. Using time-lapse microscopy to measure the division times of thousands of individual S. cerevisiae cells across different genetic and environmental backgrounds, we find that the length of individual cells’ division times can vary substantially between clonal individuals and that sublineages often show epigenetic inheritance of division times. By combining these experimental measurements with mathematical modeling, we find that, for a given mean division time, increasing heterogeneity and epigenetic inheritance of division times increases the population growth rate. Furthermore, we demonstrate that the heterogeneity and epigenetic inheritance of single-cell division times can be linked with variation in the expression of catabolic genes. Taken together, our results reveal how a change in noisy single-cell behaviors can directly influence fitness through dynamics that operate independently of effects caused by changes to the mean. These results not only allow a better understanding of microbial fitness but also help to more accurately predict fitness in other clonal populations, such as tumors.

Introduction

The fitness of a population depends on the reproductive performance of each of the individuals in the population. However, populations can be very heterogeneous, for example, due to differences in so-called life-history traits such as the kinetics of reproduction, age, and mortality [1]. Interestingly, many studies have revealed that even clonal populations in homogenous environments can show substantial levels of heterogeneity [2–12]. For example, microbial populations that are growing in the exponential phase show a considerable heterogeneity in the length of doubling (division) times (DTs) between different cells [13–19]. Similarly, cell-to-cell growth rate heterogeneity also occurs in other clonal cell populations, such as tumors [20–22]. While such biological noise in growth behavior has often been interpreted to have a direct negative impact on population-level growth rate [2, 23, 24], this effect has rarely been quantified and analyzed in detail [25].

Gene expression noise, i.e., stochastic variability in gene expression, is a key factor believed to contribute to differences between cells in a clonal population [2, 26–29]. Gene expression noise can be a disadvantageous imperfection, for example, when a robust and precise physiological response to an environmental change is required to maintain high fitness [30–33]. However, phenotypic heterogeneity arising from gene expression noise can also be part of a bet-hedging strategy, for example, by creating subpopulations that are prepared for changing or adverse conditions, often at a fitness cost in the current environment [7, 9, 34–37]. Similar to noise in single-cell growth, the direct quantitative impact of gene expression noise on population-level fitness has received little attention [7, 9, 34, 38–40].

Here, we use a combination of modeling and experimentation to investigate in detail how key life-history traits, including mean, variation, and epigenetic inheritance of DTs, affect a population’s fitness. Using time-lapse microscopy, we acquired single-cell DT distributions for a diverse range of genetically distinct Saccharomyces cerevisiae yeast strains growing exponentially on medium supplied with different carbon sources. Measurements of mother and daughter cell DTs indicate that certain strain/medium combinations yield noisy DT distributions, with substantial epigenetic inheritance of DT within sublineages. A stochastic model reveals that DT variability within mother and daughter fractions and the epigenetic inheritance of DT increase the population growth rate considerably beyond the predictions of a simple deterministic model. We show that this surprising result can be explained by a complex evolution toward a steady-state distribution of single-cell growth rates within the population. Finally, using a reverse-genetics approach, we show how changes in gene expression of catabolic genes can contribute to noisy single-cell growth behaviors. Together, our results show how variability in life-history traits across clonal individuals can sometimes counterintuitively affect population-level growth rates.

Results

Measuring Single-Cell DTs Using Automated Live-Cell Microscopy

To investigate growth at the single-cell level, we used automated time-lapse microscopy to measure key life-history traits, including mean, variance, and epigenetic correlations of DTs of single cells in the clonal populations of exponentially growing yeast cells (Experimental Procedures). We acquired time-lapse growth records for ten genetically distinct yeast strains growing in up to seven different growth media. By varying the carbon source, we were able to analyze single-cell DTs across a wide range of population growth rates (n = 41 experiments; see Dataset S1). These population growth rates were measured on solid media by tracking microcolony growth and in liquid media using a colony-counting assay (Supplemental Experimental Procedures; Dataset S3).

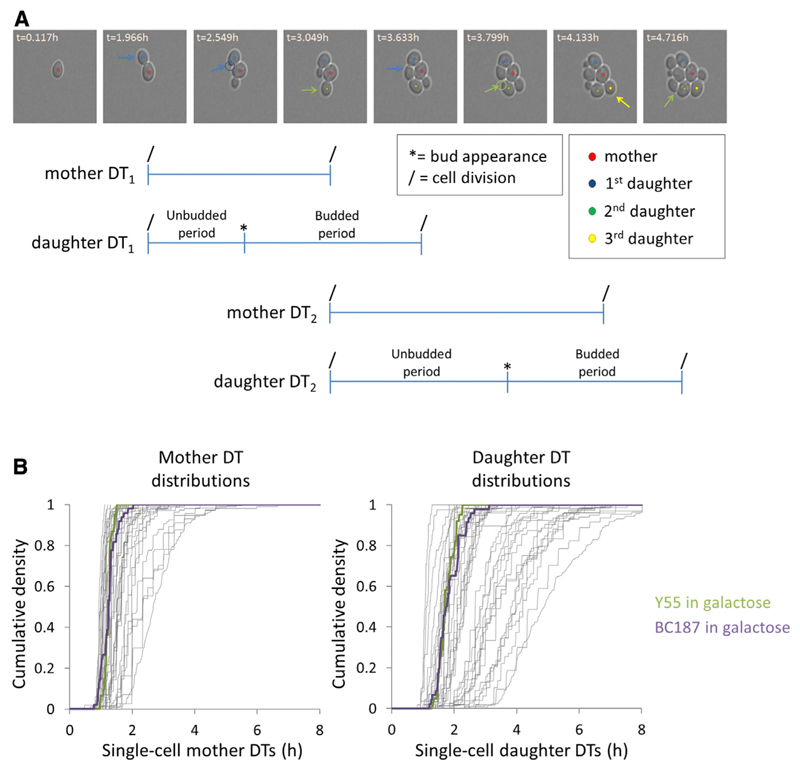
For each experiment, we analyzed the time-lapse movies by tracking the growth of individual cells within 16–113 microcolonies, yielding a total number of more than 5,500 single-cell DTs (Experimental Procedures; Dataset S1). Figure 1A and Movie S1 show how we measured the single-cell DTs. In our analyses, we distinguish between mothers (cells that have already completed a bud) and daughters (newborn cells that have not completed a bud yet). For each experiment, this analysis yields mother and daughter DT distributions, which are represented in Figure 1B.

Figure 1. Measurement of Single-Cell Division Times of Mother and Daughter Cells Using Time-Lapse Microscopy.

(A) A time-lapse microscopy image series of S. cerevisiae strain BY/S288c growing in YP + 3% glucose is shown to indicate how cell division events (indicated by the arrows) were scored. Doubling times (DTs) are determined by the time (t) difference between consecutive cell divisions. For daughter cells, the DT is divided into an unbudded period and a budded period, based on the appearance of the first bud.

(B) Mother DT (left) and daughter DT (right) distributions for ten genetically different yeast strains in up to seven different growth media (n = 41 experiments). The distributions highlighted represent Y55 (green) and BC187 (purple) growing in 2.5% galactose.

Mother DT₁, the first doubling time of the mother cell; mother DT₂, the second doubling time of the mother cell; daughter DT₁, the doubling time of the first daughter cell; daughter DT₂, the doubling time of the second daughter cell. See also Figure S1A and Movie S1.

DT Variability and Epigenetic Inheritance Are Condition and Strain Dependent

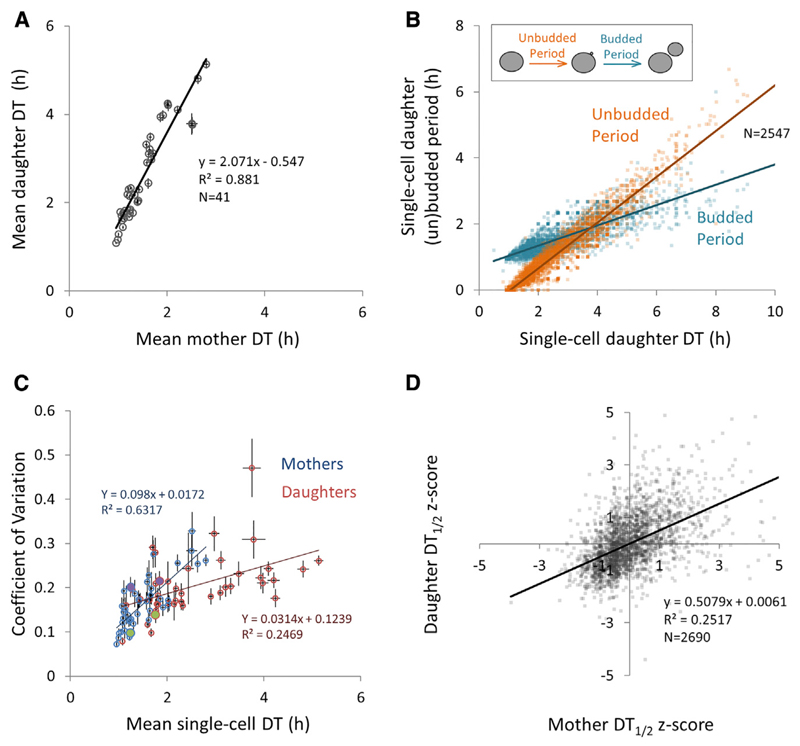
Several trends emerged from this dataset. First, it is clear that, although there is considerable variability in mean single-cell DTs across strains and environments, mean daughter and mother DTs display a striking linear relationship (Figure 2A; R² = 0.881, p < 2.2e–16). We also find that the large increase in mean daughter DTs at slower growth rates is mostly accounted for by an increase in the length of the unbudded period of the daughter cells (Figure 2B).

Figure 2. Architecture of Individual Yeast DT Traits.

(A) Mean mother and daughter DTs are linearly correlated across different yeast strains growing exponentially in different carbon sources.

(B) The lengths of the unbudded and budded periods are plotted against the total daughter DT, with each data point representing a single-cell measurement (data comprise all usable daughter DT measurements obtained in this study; n = 2,547 cells).

(C) DT CoV is plotted against mean mother (blue) and daughter (red) DTs. The green and purple fills (respectively, the strains Y55 and BC187, growing in 2.5% galactose) illustrate how some strains can have the same mean DT but different variance.

(D) The DT length is epigenetically inherited across closely related cells within a lineage. This graph shows the correlation between DTs of a mother and her most recently born daughter (Z scores of mother DT_1/2 versus Z scores of daughter DT_1/2) across the whole dataset.

All error bars represent bootstrapped SDs. Mother DT_1/2, the first or second doubling time of the mother cell; daughter DT_1/2, the doubling time of the first or second daughter cell. See also Supplemental Experimental Procedures, Figures S1B–S1G, and Dataset S1.

In order to statistically summarize the variability (or noise) in DTs for mother and daughter cells, we calculated the coefficient of variation (CoV; SD/mean). This trait is partially correlated with the mean DT (Figure 2C). However, 37% and 75%, respectively, of the variability in mother and daughter CoVs is left unexplained by the mean DT, which implies that DT noise in strains varies quite independently of the mean. For example, the strains Y55 and BC187 growing in galactose have very different DT CoVs at similar mean DTs (BC187 versus Y55; mother DT CoV = 0.201 versus 0.098; daughter DT CoV = 0.215 versus 0.139; Figures 1B and 2C).

Apart from raw DT values, our dataset also allowed us to follow how DTs were correlated between mothers and daughters (Figure 1A; Figure S1A). Using these genealogical relationships, we investigated whether there is epigenetic inheritance of the DT length by measuring correlations between individual DTs within lineages [41, 42] (Figure S1). We found that, on average, the strongest DT correlation exists between a mother and her most recently born daughter cell (R² = 0.2517; Figure 2D). In contrast, the average correlation between consecutive DTs of a given mother was much weaker (R² = 0.0153; Figure S1D). These traits are independent of mean and CoV in DT (Dataset S4). Notably, across our 41 experiments, certain strain/condition combinations displayed considerably higher DT correlations than others (Dataset S1). For example, for BY/S288c growing in palatinose, we found that the R² of both genealogical relationships is higher than 0.4 (discussed later).

Using this dataset, we used linear regression to investigate which DT characteristics best explain population-level growth. We found that a simple linear model based only on the DT means is highly predictive of population-level growth rate (R² = 0.880, p < 2.2e–16; Dataset S4). The accuracy of this model is not significantly improved by adding the DT CoV and DT correlations as parameters (Dataset S4).

An Individual-Based Model that Combines Single-Cell Variance and Epigenetic Behavior to Predict Population-Level Growth Rates

To gain insight into how the mean, noise, and epigenetic inheritance of single-cell DTs affect population-level growth behavior, we used mathematical analysis and simulation. Previously, an elegant single-cell model for budding yeast population growth was proposed by Hartwell and Unger [43]. In this deterministic model, mothers and daughters are modeled to grow at a fixed DT (measured as the arithmetic mean of the empirical DT distributions).

Deterministic Model

$$\mathit{\text{mother}}DT={\mu }_{\mathit{\text{mother}}}$$

$$\mathit{\text{daughter}}DT={\mu }_{\mathit{\text{daughter}}}$$

This model can be solved analytically, allowing the prediction of population growth rate during steady-state growth [43, 44] (Experimental Procedures).

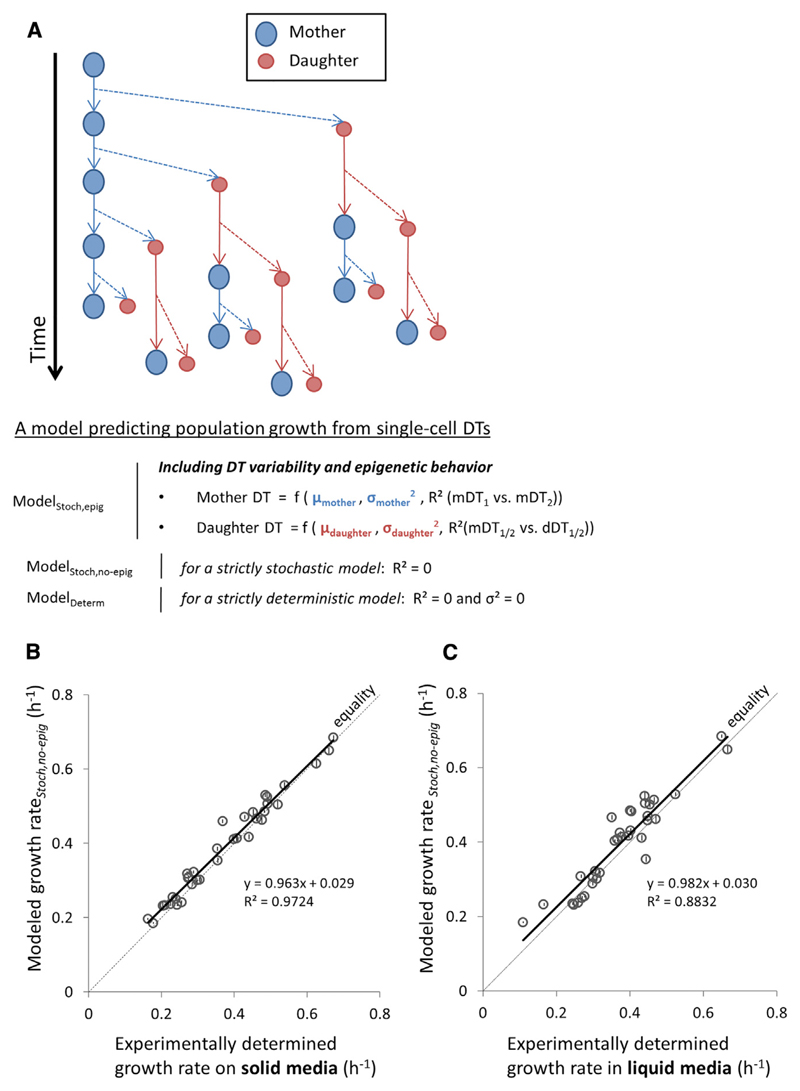
Importantly, this deterministic model considers only the arithmetic mean of mother and daughter subpopulations and does not take into account the inter-individual variability. To explore the effect that single-cell variability in DTs could have at the population level, we developed an individual-based model of population growth that accounts for variance and epigenetic inheritance of cellular DTs. In our model, all cells divide at variable DT lengths, which are randomly assigned to them by sampling from a distribution specific for the mother and daughter cells (Figure 3A). For mathematical simplicity, we describe the model in terms of the parameters of a normal distribution that were fitted to empirical DT measurements, which showed a good fit for the data (Dataset S2; Supplemental Experimental Procedures). However this analysis can be extended to other distributions, including simply the empirical DT distribution (Figure S4; Supplemental Experimental Procedures).

Figure 3. An Individual-Based Model to Predict Population Growth Rate.

(A) All cells are born as daughter cells (originating from the dashed arrows) and become mothers after completion of their first bud. At birth or after the completion of a bud, each cell is assigned a new DT that is dependent on the DT variability and epigenetic DT behaviors (Model_Stoch,epig). The model can also be run without taking into account epigenetic behaviors (Model_{Stoch,no-epig}) or stochasticity (Model_Determ). See also the Results section.

(B) Modeled population growth rates (Modeled growth rate_{Stoch,no-epig}) versus growth rates measured on solid media (microcolony growth rates). Microcolony growth rates were measured by microscopically tracking the cell count increase of microcolonies over time.

(C) Modeled population growth rates (Modeled growth rate_{Stoch,no-epig}) versus growth rates measured in liquid cultures.

Error bars represent bootstrapped SDs. mDT₁, the first doubling time of the mother cell; mDT₂, the second doubling time of the mother cell; mDT_1/2, the first or second doubling time of the mother cell; dDT_1/2, the doubling time of the first or second daughter cell. See also Supplemental Experimental Procedures and Figures S2, S3, and S6.

Stochastic Model, Without Epigenetics

$$\mathit{\text{mother}}DT=𝒩\left({\mu }_{\mathit{\text{mother}}},{\sigma }_{\mathit{\text{mother}}}^2\right)$$

$$\mathit{\text{daughter}}DT=𝒩\left({\mu }_{\mathit{\text{daughter}}},{\sigma }_{\mathit{\text{daughter}}}^2\right)$$

Such a stochastic model does not yet take into account the epigenetic inheritance of DTs, since DTs are distributed randomly and independently of previously assigned DTs. To include the effect of epigenetic inheritance of DTs on the population growth rate, we expanded our stochastic model so that the choice of new DTs also depends on previous mother DTs (Figure 3A; Figure S2). For each cellular lineage in the simulation, previously assigned DTs are used as an input to determine new DTs (the output). The set of equations used to determine new DTs constitute a transfer function that returns a series of output DTs matching the empirical DT distribution. Furthermore, the transfer function’s parameters can vary the strength of the correlation (R²) between the input and output distributions.

Stochastic Model, With Epigenetics

$$\mathit{\text{mother}}DT=D{T}_{\mathit{\text{output}},\mathit{\text{zscore}}}*{\sigma }_{\mathit{\text{mother}}}+{\mu }_{\mathit{\text{mother}}}$$

$$\mathit{\text{daughter}}DT=D{T}_{\mathit{\text{output}},\mathit{\text{zscore}}}*{\sigma }_{\mathit{\text{daughter}}}+{\mu }_{\mathit{\text{daughter}}}$$

$$D{T}_{\mathit{\text{output}},\mathit{\text{zscore}}}\sim 𝒩\left(A\times D{T}_{\mathit{\text{input}},\mathit{\text{zscore}}},{\sigma }_{\mathit{\text{transfer}}}^2\right)\mathit{\text{with}}{\sigma }_{\mathit{\text{transfer}}},A\in \left[0,1\right]$$

These equations introduce two new parameters that reflect the extent of DT correlation: ${\sigma }_{\mathit{\text{transfer}}}^2$ and A. In the Supplemental Information, we show that, for certain parameter combinations, when provided with a series of normally distributed input DTs, these functions return a series of normally distributed output DTs (Figure S2B). Each combination of A and ${\sigma }_{\mathit{\text{transfer}}}^2$ leads to a certain correlation (R²) between the input and output distributions. In this way, the R² values of the experimentally determined DT correlations are used to choose the parameters A and ${\sigma }_{\mathit{\text{transfer}}}^2$ for strain/condition-specific modeling.

To obtain population growth rate estimates for our stochastic model, we ran Monte Carlo simulations of population growth based on our empirically measured DTs (Supplemental Experimental Procedures). We ran the model under different assumptions: (1) strictly deterministic, (2) strictly stochastic (without epigenetic effects), and (3) including both DT variability and epigenetic behavior (Figure 3A). We found that all models accurately predict experimentally measured population growth rates made on solid medium and in liquid culture (Figures 3B and 3C; Figure S3). In other words, the deterministic model predicts experimentally measured population-level growth with an accuracy very similar to that of the stochastic and epigenetic models, suggesting that the DT mean is the strongest determinant of population growth rate across our dataset of growth measurements in a wide range of environments. Consistent with this, as previously mentioned, we found that, across all experiments in our dataset, the mean DT alone statistically explains 88% of population-level growth rate (Dataset S4). However, the results in the next paragraphs indicate that, for certain environments and strains, inter-individual variation and epigenetic inheritance of DTs become important and also significantly affect the population-level growth.

Heterogeneous Single-Cell Growth Affects Population-Level Fitness

Our growth simulation model allowed us to address two key questions about the potential population-level effects of our single-cell observations: (1) What role does variance in single-cell DTs play in population fitness? (2) What role does epigenetic inheritance in single-cell DTs play? Contrasting our model’s predictions of population-level growth rate with the prediction of the classic deterministic model allowed us to measure the effect that these factors can have on fitness.

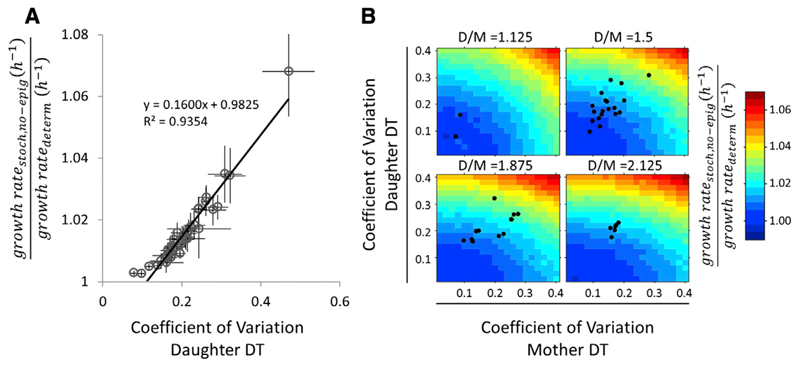
To attack the first question of how variability in DTs can affect population-level behavior, we compared our stochastic model with the deterministic model across our 41 experiments. This analysis revealed that a deterministic model can underestimate population growth rate by up to 4%–7%, depending on the type of distribution used in the simulation (Figure 4A; Figure S4A). Further analysis indicates that DT CoV explains nearly all of this growth rate increase (R² = 0.96, p < 2.2e−16). Even when controlling for the weak covariation between DT mean and DT CoV (Figure 2C), variation in single-cell DT alone can explain 63% of this growth rate increase (p < 2.2e−16; Dataset S4; Supplemental Experimental Procedures).

Figure 4. Heterogeneous Single-Cell Growth Affects Population-Level Growth Rates.

(A) The ratio of predicted population growth rates of Model_{Stoch,no-epig} over the deterministic model is plotted against the daughter DT CoV for all experiments in the dataset. Error bars represent bootstrapped SDs. Similar results are observed when using Gamma and Pearson system distributions or the empirical distributions.

(B) The predicted population growth rate depends on the variability within the mother (M) and daughter (D) DT distributions and the level of mother-daughter mean asymmetry. At each level of asymmetry, the mother DT CoV and daughter DT CoV were varied independently, and the ratios of the predicted population growth rates of Model_{Stoch,no-epig} over the deterministic model were plotted as heatmaps. The black dots represent the CoV values observed in our dataset plotted on the heatmap with the closest corresponding mother-daughter asymmetry.

See also Supplemental Experimental Procedures and Figure S4.

We used stochastic simulations to systematically investigate how these aspects of DT variation affect population-level growth. Consistent with our statistical observations, these analyses indicated that the DT CoV has a large effect on the population growth rate across the wide range of values in our experimental measurements (Figure 4B). By contrast, although we found that skewness and kurtosis can have large population-level growth rate effects, such effects are negligible in the parameter space that we observed in our dataset (Figures S4A and S4B).

The aforementioned results indicate that, given a constant mean DT, stochastic variation in DTs increases growth rate. To understand how this counterintuitive effect occurs, we first have to consider the growth rate of each single cell, which is given by ln(2)/DT. Importantly, given a DT distribution with mean = μ and SD > 0, the mean of the corresponding growth rate values will actually be higher than the growth rate of the mean DT = ln(2)/μ. This effect is more generally known as Jensen’s inequality, which states that the mean of a set of values that have undergone a convex transformation f(x)—in this case, growth rate = ln(2)/DT—is equal to or higher than the same transformation of the mean of these values (or mean[f(x)] ≥ f(mean[x])). Therefore, for a given mean, adding noise to a single-cell DT distribution has the potential to increase the population growth rate, since, on average, cells are assigned faster growth rates over the course of each doubling.

However, Jensen’s inequality alone is not sufficient to explain how population-level growth rate changes with increasing DT noise. We also have to take into account that the single-cell DT distribution evolves with time to reach a steady state that is enriched with slowly growing cells (Figure S4D). This is because individuals with short DTs finish their doubling more quickly than cells with a long DT, while new individuals have equal chances of growing with a long or a short DT. In the Supplemental Information, we show that it is the arithmetic average of the single-cell growth rates at steady state that equals the population-level growth rate. Therefore, the enrichment of slower growing individuals during steady state has the potential to reduce, or even counteract, the population growth rate increase that is predicted by Jensen’s inequality. Combining both effects, our stochastic model shows that there is a net population growth rate increase, which is, however, lower than the arithmetic mean of the sampled growth rate (ln[2]/DT) distribution (Figure S4C).

The effect of increased DT noise on population-level growth can be non-trivial, especially given that the variance and mean of single-cell DTs can be largely independent phenotypic traits (Figure 2C). The results imply that a change in DT CoV can yield a considerable difference in fitness and, thus, a significant selective advantage over evolutionary timescales. Indeed, a simple simulation using the stochastic model shows that, when the mean DT is kept constant, mutants with more noisy DT distributions have a selective advantage compared to a population with less noisy DT distributions. Moreover, these mutants reach fixation at similar frequencies as mutants that have the same fitness advantage by having a shorter DT mean but the same DT noise (Supplemental Experimental Procedures). Together, these results are at odds with the common intuition that growth noise is always detrimental for the population-level fitness.

Epigenetic Inheritance of Single-Cell DTs Further Increases Population-Level Fitness

To investigate the effect of epigenetic DT inheritance on population growth rate, we compared the predicted population growth rates from the stochastic-epigenetic model with those of the strictly stochastic model (Figure 5). For each specific strain/condition combination, we modeled two experimentally observed DT correlations, including the correlation between consecutive mother DTs and the correlation between the DTs of a mother and her most recently born daughter (Figure 5A; Figure S2C).

Figure 5. Epigenetic Inheritance of Single-Cell Growth Rates Further Increases Population-Level Growth Rates.

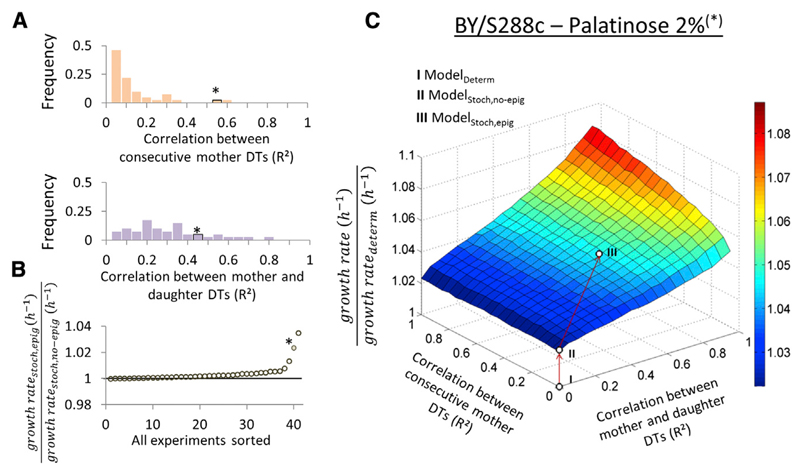
(A) Two experimentally observed DT correlations were considered in the model: (top) mother DT₁ versus mother DT₂ and (bottom) mother DT_1/2 versus daughter DT_1/2. Here, histograms of the R² values of these correlations are shown per experiment. The asterisk marks the bin that includes BY/S288c in 2% palatinose.

(B) The ratio of the growth rates of the model with epigenetics (Model_Stoch,epig) and without epigenetics (Model_{Stoch,no-epig}) were calculated for each experiment and sorted from low to high. The asterisk marks the data point corresponding to BY/S288c in 2% palatinose.

(C) The effect of epigenetic single-cell DT correlations on the predicted population-level growth rate is illustrated with a heatmap. Colors indicate fold increase of a given model over the deterministic model. The dots (I–III) are predictions of the deterministic model (I) or the stochastic model without (II) or with (III) epigenetics for BY/S288 growing in 2% palatinose.

See also Figure S5.

Viewed across our dataset, epigenetic inheritance has only a small effect on population growth rate compared to predictions made when there is no individual DT correlation (Figure 5B). However, some strain/condition combinations show a significant population-level growth rate increase when epigenetic effects are considered, especially for strain/condition combinations that show both high single-cell DT variability and high epigenetic DT inheritance (Figure S5). We illustrate this in Figure 5C with a fitness landscape of the strain BY/S288c growing in palatinose. The growth-rate-increasing effect of epigenetic DT inheritance can be intuitively understood by its effect on the steady-state DT distribution. Even though cells with a short DT finish their doubling more quickly, because of the epigenetic factor, they are more likely to give rise to fast-growing cells themselves. This diminishes enrichment for slowly dividing cells, leading to a steady-state DT distribution containing more quickly dividing cells than under the assumption of a purely stochastic model (Figures S4D and S4E).

Epigenetics Can Amplify the Heterogeneity of Growth Rates between Small Populations

We found that single-cell DT variability and epigenetic DT inheritance can affect population-level growth rates at large population sizes (Figures 4 and 5). Likewise, we expected that these parameters could also considerably affect the variability of growth rates between different (isogenic) populations, especially at small population sizes when the variability in single-cell DTs might not yet be averaged out [7, 9, 24, 45].

To test for these effects, we used a non-parametric statistical comparison between our model’s predictions and empirical measurements made at small population sizes (Supplemental Information). These analyses revealed that, for strain/condition combinations where the mother-daughter DT correlation is low (R² < 0.35), epigenetics plays a small role in microcolony variability. However, for strain/condition combinations where the mother-daughter DT correlation is high (R² > 0.35), simulations of microcolony growth rate distributions that account for epigenetic effects are consistently closer to the measured values (Figure S6B; Supplemental Information). Together, these results indicate that, in many cases, microcolony growth variability is simply the result of stochastic variability in single-cell DTs. However, in other cases where epigenetic effects are strong, this can lead to further increases in microcolony growth rate variability.

Overexpressing the Genes Required for Growth Reduces Heterogeneity and Epigenetic Inheritance of Single-Cell DTs

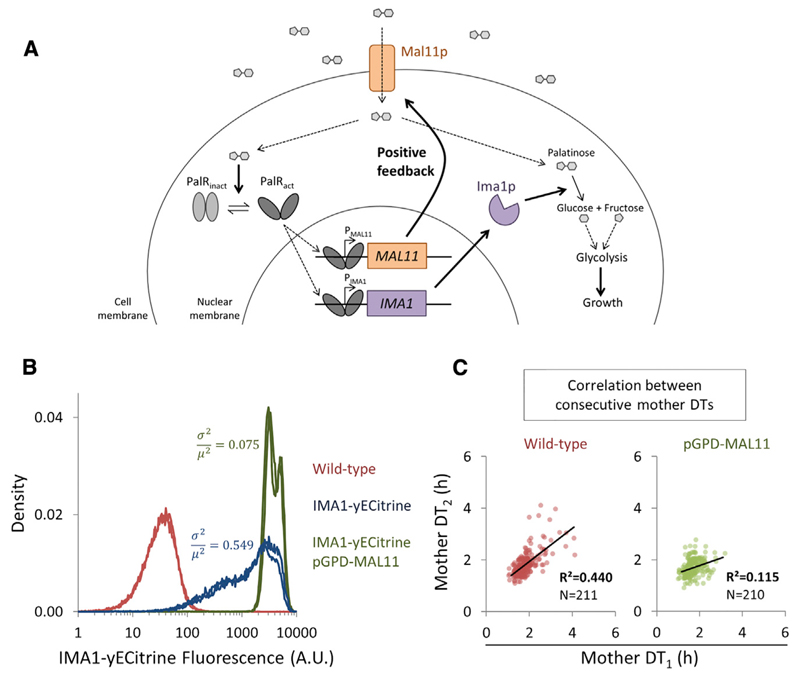
We set out to identify a molecular mechanism that might underlie stochastic and epigenetic single-cell DT variability. To explore this, we examined gene expression and single-cell growth in palatinose, a condition that gave rise to both a high degree of single-cell DT variability and high epigenetic DT inheritance (Figure 5A). We reasoned that expression of the genes necessary for growth on this sugar might affect the observed growth variability. To grow fermentatively on palatinose, S. cerevisiae needs to transport the sugar through the alpha-glucoside transporter Mal11p and cleave the sugar intracellularly using an alpha-1,6-glucosidase enzyme (enzyme encoded by two paralogous genes, IMA1 and IMA5) [46–48]. The expression of MAL11 and IMA1 is induced by two transcriptional activators (MAL13 and YFL052W), both of which are essential for growth on palatinose [46]. The regulatory gene network is visualized in Figure 6A.

Figure 6. Overexpressing the Genes Required for Growth Reduces the DT Variability and Epigenetic DT Inheritance.

(A) Palatinose is transported into the cytoplasm by Mal11p, and broken down by Ima1p. In the presence of intracellular palatinose, MAL11 and IMA1 expression is induced by two transcriptional activators (represented here by PalR), a typical positive-feedback motif.

(B) Flow cytometry analysis of the effect of MAL11 overexpression. Shown are traces of IMA1 expression of the WT BY/S288c (red); a strain in which MAL11 and IMA1 have been fluorescently tagged (blue); and the dually tagged fluorescent strain, in which MAL11 has been overexpressed (green). Gene expression noise is indicated as σ²/μ² [26].

(C) Epigenetic DT inheritance in the WT and a MAL11 overexpression strain. In this plot, jitter was added in both dimensions to represent better the density of the observations.

We constructed a strain bearing fluorescently tagged IMA1(-yECitrine) and MAL11(-mCherry) alleles and measured the expression of these two genes with flow cytometry. The results indicate that, while both genes are, on average, highly expressed in palatinose, they exhibit high expression noise (Figure 6B). Moreover, the expression levels of MAL11 and IMA1 show a significant correlation at the single-cell level (R² = 0.37 ± 0.01 of log-transformed fluorescence; p < 0.001). We hypothesized that noise in the gene expression of Ima1p could be reduced by overexpressing MAL11, since this transporter is part of a positive-feedback loop in the regulatory network (Figure 6A). Indeed, overexpression of MAL11 in the fluorescently tagged strain (using an extra untagged copy of MAL11 expressed from a constitutive GPD promoter) results in reduced network noise, with much more homogeneous Ima1p expression levels (Figure 6B), leading to an approximately 7-fold reduction in single-cell expression noise of Ima1p-mCitrine (gene expression noise σ²/μ² [26] lowers from 0.549 to 0.075).

Next, we investigated whether these changes in the expression of the palatinose utilization pathway would affect DT variability and epigenetic inheritance by measuring single-cell growth using timelapse microscopy. The results show that both single-cell DT variability and epigenetic DT inheritance are strongly reduced by overexpression of MAL11 compared to wild-type (WT) control cultures (p = 0.011 and 0.052 for mother and daughter DT CoVs, respectively; Figure 6C). These changes are comparatively large as well: across all measurements made in this study, variability in the daughter DT distributions (the residuals of the plot of CoV versus mean; Figure 2C) shifts from the 84th percentile to the 12th percentile (p = 0.052), and variability in the mother DT distributions is reduced from the 88th percentile the 60th percentile (p = 0.011; Supplemental Information; Dataset S4). Finally, we found a strong reduction in epigenetic DT inheritance; the correlation (R²) between consecutive mother DTs is reduced from 0.440 to 0.115 (p = 0.010), and the correlation between mother and daughter DTs is lowered from 0.485 to 0.265 (p = 0.045). In contrast, the effect of MAL11 over-expression on the mean mother DTs and mean daughter DTs was weak and opposite for mothers and daughters (mean mother DT reduced from 1.86 hr to 1.71 hr; mean daughter DT increased from 3.35 hr to 4.07 hr). Taken together, these results indicate that a single genetic modification can affect the variance and epigenetic features of single-cell DTs, with inconsistent effects on the mean. Furthermore, they show that the expression of genes required for growth can modulate DT variability and epigenetics.

Discussion

Together, our observations indicate that three life-history traits of cellular growth—mean, variance, and epigenetic inheritance of DT—are naturally variable, largely independent, and genetically influenced traits. Furthermore, our mathematical models and simulations indicate that these traits have the potential to significantly affect population-level fitness. Most intuitively, population-level growth rate is affected by the mean DT. However, for a given mean DT, individual-level variation in DT can further influence population-level growth, with higher variance counter-intuitively increasing fitness (Figure 4). Finally, for a given level of mean and variation, increasing epigenetic inheritance in DTs can further increase population-level growth (Figure 5). We show that the effect of DT variation and epigenetic inheritance occurs through a complex evolution toward a steady-state distribution of single-cell growth rates within the population. These results are in line with results obtained by Tăvnase-Nicola and ten Wolde (2008) [25], who used mathematical models to show that Gaussian noise in the instantaneous single-cell growth rate could increase population growth rates.

Given that increased DT variation and epigenetic inheritance of DTs have the potential to increase population-level growth rate, one might wonder whether, like the mean growth rate, these traits can, in principle, be subject to natural selection. Indeed, a simulation indicates that mutants with more noisy DT distributions, but the same mean DT, can reach fixation in populations of WT cells (Supplemental Experimental Procedures). These results show that these mutants can overcome the drift barrier to reach fixation at frequencies similar to that of a mutant that has the same fitness advantage by having shorter mean DTs, but the same DT noise. Furthermore, for natural selection to act directly on the phenotype of growth variability, it would have to be a genetically encoded trait. Our results suggest that there are, indeed, significant genetic determinants that shape the level of growth noise (Figure 6) [9]. We have shown that noisy single-cell growth on palatinose can be lowered by the overexpression of positive feedback in a catabolic gene circuit (Figure 6) [10], with inconsistent effects on the mean. Together, these findings suggest that the trait of increased DT variation and epigenetic inheritance can, in principle, rise in frequency via natural selection. That said, it seems likely that selection mainly acts on the mean DT, with the effect of noise, at best, playing a less prominent role.

Finally, our results and model should be more generally useful for predicting the growth rates of populations consisting of different subgroups that have variable growth rates, where clonal variability and/or epigenetic effects are strong [3, 49–53]. For example, tumor growth is shaped by heterogeneous single-cell growth behaviors; however, the degree to which these traits affect population-level growth has not been quantitatively described. Our findings, therefore, provide a framework for more detailed models of cellular growth and help explain how individual-level variability affects population growth dynamics in diseases that involve clonal growth, such as cancer and microbial pathogenesis.

Experimental Procedures

Yeast Strains and Growth Media Used

For the time-lapse microscopy experiments, a genetically diverse set of yeast strains was used. We performed 12 experiments using the lab strains BY/S288c and SK1 [9, 54, 55], 14 experiments using homozygous diploid strains derived from wild isolates (YPS606, L-1374, Y12, DBVPG1106, DBVPG6765, Y55, YPS128, and BC187; [55]) and 15 experiments using experimentally evolved isolates [9]. For the data shown in Figure 6, a set of three strains that are not included in the dataset were used (derived from BY/S288c). For construction details, refer to Supplemental Experimental Procedures. All experiments were performed at 30°C using YP (yeast peptone)-based media. The media that were used were YP supplemented with 3% and 10% glucose, 20% maltose, 2.5% galactose, 2% palatinose, 2% glycerol, and 2% glucose + 5% ethanol. For more details on the specific combinations of strains and media used in the experiments, see Dataset S1.

Acquisition of Time-Lapse Movies

All strains were first pre-grown in liquid culture at low cell densities (<2 · 10⁶ cells per milliliter) by serially passaging them to achieve balanced steady-state populations (minimally, 16 hr). These cultures were then sandwiched between an agar gel containing the appropriate medium and a coverslip, allowing us to track hundreds of single cells at various positions on the agar pad in a single experiment by periodically taking differential interference contrast (DIC) microscopic images [9]. See also the Supplemental Experimental Procedures.

Analysis of Single-Cell DTs

In concordance with previous studies [43], cells were scored either as mothers or daughters. By definition, all cells are born as daughters and become mothers only after finishing their first cell division. For details on how these DTs were scored, see Figure 1A, Movie S1, and Supplemental Experimental Procedures.

Predicting Population Growth Rates Using the Stochastic Model

Population growth rates under the stochastic model are predicted using Monte Carlo simulations (see the Supplemental Experimental Procedures). Also, see the Results section and the Supplemental Information for information on the theoretical framework behind the model, as well as the derivation of mathematical equations used in the model.

Predicting Population Growth Rates Using the Deterministic Model

We have calculated predicted population growth using the classic model by [43], using the following equation: e(^{−popGR×μ_mother}) + e(^{−popGR×μ_daughter}) = 1, with popGR as population growth rate, μ_mother as mean mother DT, and μ_daughter as mean daughter DT (Equation 8 in [43]).

Supplemental Information

Supplemental Information includes Supplemental Experimental Procedures, six figures, five datasets, and one movie and can be found with this article online at http://dx.doi.org/10.1016/j.cub.2016.03.010.

Highlights.

• Single-cell division times of yeast strains were measured in different conditions

• Individual cells show noise and epigenetic inheritance of division times

• For a given mean division time, noise and epigenetic phenomena increase fitness

• Catabolic gene expression can contribute to division time noise and epigenetics