Joint Prediction of Longitudinal Development of Cortical Surfaces and White Matter Fibers from Neonatal MRI

Abstract

The human brain can be modeled as multiple interrelated shapes (or a multishape), each for characterizing one aspect of the brain, such as the cortex and white matter pathways. Predicting the developing multishape is a very challenging task due to the contrasting nature of the developmental trajectories of the constituent shapes: smooth for the cortical surface and non-smooth for white matter tracts due to changes such as bifurcation. We recently addressed this problem and proposed an approach for predicting the multishape developmental spatiotemporal trajectories of infant brains based only on neonatal MRI data using a set of geometric, dynamic, and fiber-to-surface connectivity features. In this paper, we propose two key innovations to further improve the prediction of multishape evolution. First, for a more accurate cortical surface prediction, instead of simply relying on one neonatal atlas to guide the prediction of the multishape, we propose to use multiple neonatal atlases to build a spatially heterogeneous atlas using the multidirectional varifold representation. This individualizes the atlas by locally maximizing its similarity to the testing baseline cortical shape for each cortical region, thereby better representing the baseline testing cortical surface, which founds the multishape prediction process. Second, for temporally consistent fiber prediction, we propose to reliably estimate spatiotemporal connectivity features using low-rank tensor completion, thereby capturing the variability and richness of the temporal development of fibers. Experimental results confirm that the proposed variants significantly improve the prediction performance of our original multishape prediction framework for both cortical surfaces and fiber tracts shape at 3, 6, and 9 months of age. Our pioneering model will pave the way for learning how to predict the evolution of anatomical shapes with abnormal changes. Ultimately, devising accurate shape evolution prediction models that can help quantify and predict the severity of a brain disorder as it progresses will be of great aid in individualized treatment planning.

1. Introduction

Multimodal MR imaging offers unprecedented insights into different facets of brain development. With the increasing availability of longitudinal postnatal brain imaging data, one can now track dramatic spatiotemporal changes in both white matter (Dubois et al., 2014) and gray matter (Gilmore et al., 2007) during the first years of postnatal development. The trajectories of these changes are often characterized using spatiotemporal shape models. However, great challenges arise when the shapes of different structures exhibit contrasting developmental behaviors. For instance, the cortical surface can be modeled as a shape that undergoes a diffeomorphic (i.e., smooth and invertible) evolution, whereas white matter pathways undergo a non-diffeomorphic evolution as they elongate and bifurcate with growth due to active myelination (Deoni et al., 2011).

Devising a robust and accurate framework for predicting, based on neonatal data, the development of multiple interlinked shapes, such as cortical surfaces and white matter tracts, is of great clinical interest. This allows identification of aberrant developmental patterns in case-control settings. There is a growing body of evidence in the neuroscience literature indicating that the shapes of structures in the developing brain can be used as biomarkers for many neurodevelopmental disorders. For instance, hemispheric shape asymmetries appeared to be influenced by sexually dimorphic factors or by schizophrenia pathophysiology (Narr et al., 2007). In addition, the morphology of cortical gyri and sulci at birth is found to be predictive of the pathological functioning in certain developmental and neuropsychiatric disorders (Dubois et al., 2008). This motivates designing shape-based developmental prediction models to allow early diagnosis of neurodeveopmental and psychiatric illnesses that are rooted in early infancy (Lyall et al., 2014) as well as neurodevelopmental impairments in preterm infants (Kapellou et al., 2006).

Existing approaches to brain growth prediction are mainly focused on predicting the evolution of low-dimensional scalar data. For instance, Sadeghi et al. used nonlinear mixed-effects modeling to infer individual developmental trajectories for the radial diffusivity of the posterior thalamic radiation (Sadeghi et al., 2013, 2014; Gerig et al., 2016). Extension of methods as such to high-dimensional data involving multiple shapes poses significant challenges, as pointed out in (Gerig et al., 2016). (Fishbaugh et al., 2013) proposed a geodesic shape regression model rooted in the theory of currents to predict back in time subcortical shapes at 6 months from shapes at between 9 and 24 months of age. This model was further extended to integrate image data to evolve image and shape following the slope of the initial momenta vectors (Fishbaugh et al., 2014). However, for image-shape prediction, this model requires measurements at least at two time points. Even more advanced approaches still required more than one time point for prediction such as the works of (Nie et al., 2010, 2012) where a mechanical cortical growth model was devised to simulate the dynamics of cortical folding from longitudinal MRI data in the first postnatal year.

To address these problems, we introduced in (Rekik et al., 2015a,b,c) learning-based frameworks for predicting subject-specific spatiotemporal growth of the cortical surface solely from neonatal data acquired at a single time point. Although promising, these frameworks are focused only on predicting one shape (i.e., the cortical surface) and ignore other important shapes such as the white matter tracts. To the best of our knowledge, our work introduced in (Rekik et al., 2016b) is the first attempt to address this limitation by multishape modeling of both cortical surfaces derived from structural MRI and the white matter fibers derived from diffusion MRI. Building on (Rekik et al., 2015b,a,c), the proposed framework (Rekik et al., 2016a,b) employs a geodesic multidirectional varifold shape regression model to estimate a time-varying deformation velocity field that flows shapes diffeomorphically. In addition, the proposed framework harnesses fiber-to-surface connectivity for non-diffeomorphic modeling of the growth of white matter tracts. Specifically, our framework includes training and testing stages. In the training stage, for each infant, we learn from the training subjects (1) the geometric features of the cortical surface, (2) the dynamic features (i.e., evolution trajectories) of the baseline cortical surface, and (3) the fiber-to-surface connectivity features. In the testing stage, for the multishape of a testing neonatal subject, we select the best features that simultaneously predict the triangular faces on the cortical surface mesh and all the fibers traversing them at the 3, 6 and 9 months time points. Our framework affords several advantages. First, it does not require the computationally expensive process of registering thousands of fibers to establish tract-to-tract correspondence for prediction, which is prohibitive using a conventional diffeomorphic multishape registration setting as in (Durrleman et al., 2014). Second, it guides fiber prediction using the diffeomorphic cortical surface deformation trajectory, which is less complex and can be estimated more accurately than that of fiber growth trajectory. More importantly, this enables us to account for fiber connectivity changes and the occurrence of new fibers, which can cause topological changes in the connections.

However, this first work on multishape prediction had a number of limitations, which we aim to address in this paper. First, our early approaches (Rekik et al., 2015b,a, 2016b) use a single-atlas approach where shape information from a single neonatal subject in the training dataset was used to obtain the shape predictions, failing to take into account possible spatial and topographic variability. To address this, we propose to use multiple atlases to estimate a spatially heterogenous atlas that best approximates the cortical shape of a testing subject. For this purpose, we use the multidirectional varifold shape similarity metric introduced in (Rekik et al., 2015c, 2016a). Second, in our work (Rekik et al., 2016b), the fiber-surface relationship was determined based only on the neonatal time point, hence does not enforce temporal consistency. To address this, we propose to estimate spatiotemporal connectivity features from neonatal connectivity features using low-rank tensor completion (Kressner et al., 2014) to further refine the fiber selection process. Experimental results indicate that the two strategies mentioned above significantly improve the prediction accuracy in comparison with our previous method (Rekik et al., 2016b).

2. Fundamental works on longitudinal multishape prediction from a single measurement

In this section, we provide a comprehensive overview of the first works related to learning-based shape prediction for the developing infant brain. These present the building blocks of the enhanced multishape prediction model devised in this paper. For easy reference and to enhance the readability, we summarized the major mathematical notations in Table 1.

Table 1.

Major mathematical notations used in this paper.

Mathematical notation	Definition
x	3D position in ℝ3
W*	space of currents and varifolds
W	testing space
ω	testing vector field in W
KW	shape Gaussian kernel of RKHS
KV	deformation Gaussian kernel
σW	decay rate of the Gaussian kernel KW
σV	decay rate of the Gaussian kernel KV
ke	linear kernel for varifold definition
n	oriented unit normal vector in ℝ3
$\overleftrightarrow{n}$	nonoriented unit normal vector in ℝ3
ϕt	diffeomorphism (invertible and smooth mapping) at time t
vt	the deformation velocity field at time t
pk	initial deformation momentum in ℝ3 located at the control point ck
Si	observed surface at timepoint ti
${\stackrel{\sim }{S}}_0$	reconstructed virtual shape
${\stackrel{\sim }{S}}_i$	predicted surface, i > 0
$\mathcal{V}$	the dynamic cloud
${\mathcal{A}}_i$	atlas at timepoint ti
κ	principal curvature direction
Fi	ensemble of fibers
${\stackrel{\sim }{F}}_0$	virtual ensemble of fibers
${\stackrel{\sim }{F}}_i$	predicted fibers, i > 0
Mi	multishape (Si, Fi) observed at timepoint ti
πS(F)	projecting fibers F onto a surface S
fk	the two extremeties of fiber f, k ∈ {1, 2}
ξ	a triangular face (mesh)
μ	a vertex in ℝ3
μl	a vertex belonging to a labeled region l
F(ξ)	set of fibers that hit the face ξ
d(ξ, ξ′)	similarity measure between two faces ξ and xi′ in fiber properties
ε	radius of the local neighborhood search
${\mathcal{T}}_{\mu }$	low-rank tensor of size Nk × Nt × Ns defined at vertex μ
${ℰ}_{\mu }$	masking tensor of size Nk × Nt × Ns defined at vertex μ
r	multilinear rank of dimension 1 × 3
Nk	number of faces in k–ring neighborhood centered at vertex μ
Nt	number of acquisition timepoints (including the first observation)
Ns	number of all training subjects + the new testing subject
Mr	smooth manifold of tensors
PΩ	linear tensor projection onto Ω

2.1. Surface Prediction Using Geodesic Regression

We summarize here the key ingredients of the devised cortical surface shape development prediction framework in (Rekik et al., 2015b,a). These 5 will respectively address the following fundamental questions: (1) How to mathematically measure the shape of the cortical surface? (2) How to estimate the developmental trajectory of a baseline surface onto a set of subsequent observed surfaces? (3) What features we can learn from a set of training shapes and their corresponding deformation trajectories to guide the prediction of the evolution of a new baseline shape? (4) How to use these learned features to guide the cortical surface shape prediction?

2.1.1. Shape Representation

In (Rekik et al., 2015b), we quantify a shape via currents using a testing vector field ω ∈ W to linearly map the shape to a scalar in ℝ (Durrleman, 2010). This compact representation is motivated by the Faraday’s law of induction, which states that the variation of any magnetic vector field W through a surface S induces a scalar-valued current in the space of currents W^* within a wire loop delimiting S. A collection of several current measurements through the loop allows the retrieval of the geometry of surface S. This mathematically translates as integrating a testing vector field ω along the loop Ω_S with respect to the unit normal n of the surface: $S(\omega )={\displaystyle {\int }_{{\mathrm{\Omega }}_S}\omega {(x)}^{\top }}n(x)d\lambda (x)$, where dλ(x) is the Lebesgue measure on the surface at location x.

To characterize a shape, we measure how the current changes with a varying ω, which belongs to a reproducing kernel Hilbert space (RKHS) W defined by Gaussian kernel $K_W(x,y)=\exp \left(-{\left|x-y\right|}^2/{\sigma }_W^2\right)$. The reproducing kernel K_W decays at rate σ_W which represents the scale above which geometric details of the shape are investigated. Currents allow generalizable representation of shapes of different dimensions (e.g., points, curves, surfaces, etc.) and enable shape matching without point-to-point correspondence. However, they fail when surfaces with opposing normals need to be added (Durrleman et al., 2014). To overcome this limitation, Charon and Trouvé (2013) adopted varifolds for shape representation, using non-oriented normal vectors $\overleftrightarrow{n}$ and an additional linear kernel k_e defined in the tangent space to a Grassmanian manifold. A shape is then represented in the varifold space W^* as a distribution of non-oriented tangent spaces to an embedding Grassmanian manifold. Mathematically, the varifold of shape S is defined as $S(\omega )={\displaystyle {\int }_{{\mathrm{\Omega }}_S}\omega (x,\overleftrightarrow{n(x)})}\left|n(x)\right|dx$, where in this case $\omega (x,\overleftrightarrow{n(x)})$ is a function of space position x ∈ ℝ³ and the nonoriented unit vector $\overleftrightarrow{n(x)}$. This refined metric was used in the extended work (Rekik et al., 2015a) for a more accurate shape representation in the prediction framework.

2.1.2. Geodesic Diffeomorphic Shape Regression

Next, to deform a baseline shape S₀ observed at time t₀ onto a set of observed shapes {S₁, …, S_N} observed at time points {t₁, …, t_N}, we use the large diffeomorphic deformation metric mapping (LDDMM) shape deformation framework developed in (Trouvé, 1998; Beg et al., 2005), where an ambient space is deformed together with the shapes embedded in it. This framework is well-suited for modeling invertible and temporally smooth changes in anatomical shapes (Gerig et al., 2016) and was adopted to model the deformation of currents in (Durrleman, 2010; Rekik et al., 2015b) and varifolds in (Durrleman et al., 2014; Rekik et al., 2015a). The spatiotemporal deformation of a shape S₀ is characterized by a diffeomorphism (i.e., smooth and invertible mapping) ϕ_t that flows along the geodesic (i.e., shortest deformation trajectory) in time t ∈ [0, 1] (Fig. 1). The sought diffeomorphism ϕ_t satisfies the following ordinary differential equation:

$$\{\begin{array}{l}\frac{d{\varphi }_t(x)}{dt}=v_t\circ {\varphi }_t(x),t\in [0,1],\hfill \\ {\varphi }_0={\mathrm{Id}}_{{ℝ}^3}.\hfill \end{array}$$ (1)

The time-varying velocity field v_t belongs to the RKHS V defined by a Gaussian kernel K_V, which decays at a rate σ_V. The deformation was fully determined by a set of initial deformation momenta ${\left\{p_k\right\}}_{k=1,\dots ,N_c}$ associated with an estimated set of control points ${\left\{c_k\right\}}_{k=1,\dots ,N_c}$. The optimal initial deformation momenta, control points, and positions of deformed vertices are estimated through minimizing the following energy functional:

$$E=\frac{1}{2}{\displaystyle {\int }_0^1{\left|v_t\right|}_V^{2}dt+\gamma }{\displaystyle \sum _{j\in \{1,\dots ,N\}}{\Vert {\varphi }_{t_j}\cdot S_0-S_j\Vert }_{W\ast }^2.}$$ (2)

Figure 1. Training for multishape prediction.

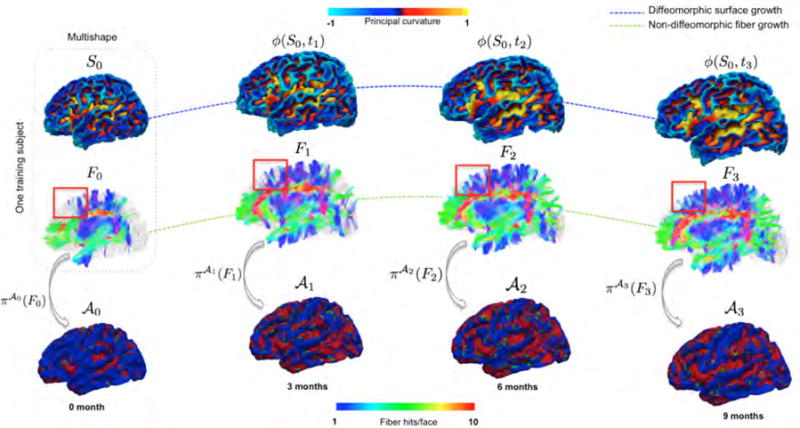
(Top row) Estimate the baseline evolution trajectory of cortical surface, characterized by diffeomorphism ϕ. (Middle row) Whole-brain deterministic tractography to estimate fiber tracts {F_i} at each acquisition time point. The red box highlights the non-diffeomorphic nature of fiber growth. (Bottom row) Fiber projection ${\pi }^{{\mathcal{A}}_i}(F_i)$ onto longitudinal atlases $\left\{{\mathcal{A}}_i\right\}$.

The velocity at any position x ∈ ℝ³ is computed as the convolution of the estimated momenta {p_k} with $K_V:v_t(x)={\displaystyle {\sum }_{k=1}^{N_c}{K}_V(x,c_k)p_k}$. The parameter γ defines the trade-off between the first term, which enforces smooth deformation by minimizing the total kinetic energy of the deformation, and the second term, which enforces closeness between the warped baseline shape ${\varphi }_{t_j}$. S₀ and the observed shapes S_j at various time points t_j. The objective functional E is minimized through gradient descent as described in (Durrleman et al., 2014). Based on (Durrleman et al., 2014; Rekik et al., 2016a), we assume that, for each subject, we have a reliable anatomical correspondences between cortical surfaces over time.

2.1.3. Feature Extraction and Shape Prediction

Geometric and Dynamic Features

We first register all baseline shapes of the training subjects into a common space, where we estimate the spatiotemporal cortical surface growth trajectory for each training infant using the method in (Rekik et al., 2016a), thereby linking all subjects in space and time. Then, we extract geometric and dynamic features from the training baseline shapes for the prediction of growth trajectories. The geometric features consist of the position x of each vertex whereas the dynamic features consist of the corresponding deformation geodesics ϕ(x, t), t ∈ [0, 1]. We collect these feature pairs (x, ϕ(x, t)) in a dynamic cloud $\mathcal{V}$. Hence, a point in the cloud determines the warped position ϕ(x, t) at any time point t of any baseline vertex at position x.

Longitudinal Atlases

Since the only available observation for prediction is the shape at the first acquisition timepoint, we hypothesized that by reconstructing the testing baseline shape using the training baseline shapes, one can easily predict its evolution trajectory since every training vertex in the cloud $\mathcal{V}$ is paired with its deformation trajectory. To this aim, we first use the training shapes in the common space to estimate a longitudinal set of shape atlases $\left\{{\mathcal{A}}_0,\dots ,{\mathcal{A}}_i,\dots ,{\mathcal{A}}_N\right\}$ for time points {t_i}, with i ∈ {0, …, N}. Each vertex on an atlas computed as the mean position of the corresponding vertices on the aligned training shapes and its deformation trajectory as the average of their corresponding training trajectories. Given the shape ${\stackrel{\sim }{S}}_0$ of a testing subject, the baseline atlas ${\mathcal{A}}_0$ is individualized to match ${\stackrel{\sim }{S}}_0$ better. This involves creating a virtual shape as we will discuss next.

Construction of Virtual Shape and Developmental Trajectories Retrieval

A virtual shape ${\stackrel{\sim }{S}}_0$ is constructed by adapting the baseline atlas ${\mathcal{A}}_0$ to the baseline testing shape S₀. It can be viewed as a reconstruction of the observed testing shape S₀ using both atlas and training data. First, we initialize the virtual shape as the baseline atlas ${\mathcal{A}}_0$. Then, vertices in ${\stackrel{\sim }{S}}_0$ are kept unchanged if they fall within an ε-proximity from the corresponding vertex in S₀. On the other hand, vertices that are beyond ε-proximity from the baseline testing shape S₀ are updated by locating the vertices in the cloud $\mathcal{V}$ that are within an ε-distance to the baseline vertex. Through averaging their positions, the vertex in the initial virtual shape is then moved to a closer proximity from the testing shape (Rekik et al., 2015b). This strategy was further refined in (Rekik et al., 2015a) by searching for the closest neighbors from the cloud with similar morphological properties as the vertex in S₀. Specifically, we locally search for the m–closest neighbors from the cloud that share the same maximum principal curvature sign with the baseline testing vertex. Ultimately, for an unmoved vertex in the virtual shape, which means that this vertex belongs to the baseline atlas, one directly predicts its evolution trajectory by retrieving the corresponding atlas deformation trajectory. As for a moved vertex in the virtual shape, its evolution trajectory is estimated through averaging the dynamic trajectories of its m–selected neighbors from the cloud.

Remark

For prediction, we averaged the inferred diffeomorphic evolution trajectories from the estimated momenta. Since we use a very small local neighborhood, we assume that at a small local scale, the average of flow of diffeomorphisms is a diffeomorphism. However, this may not apply for large spatial neighborhoods. In our future work, we intend to directly average the momenta, and then infer the evolution trajectory for generalizability and soundness.

2.2. Extension to Multishapes

We now extend the previously described single-shape framework to deal with multishapes, as presented in (Rekik et al., 2016b). In our case, a multishape M_i observed at timepoint t_i is composed of cortical surface S_i and a set of white matter tract streamlines ${ℱ}_i$. Of note, framework accounts for the non-diffeomorphic growth of the latter.

2.2.1. Surface and fiber tract measurement using respectively multidirectional and unidirectional varifold representations

As demonstrated in (Rekik et al., 2015c, 2016a), multidirectional varifolds are a better representation for surfaces, resulting in more anatomically consistent shape registration and regression. Instead of only relying on the conventional normal directions on a surface to characterize its shape, the directions of principal curvatures are used as additional information. Within the same varifold space, we measure the S as two varifolds generated along two different directions: the unoriented normal direction and the unoriented principal curvature direction, which respectively induces the varifold representations of the S as $S^{\overleftrightarrow{n}}$ and $S^{\overleftrightarrow{\kappa }}$. To estimate the deformation trajectories using multidirectional varifolds, we minimize the following energy term (Rekik et al., 2016a):

$$E_{\mathit{multidirectional}}=\frac{1}{2}{\displaystyle {\int }_0^1{\left|v_t\right|}_V^{2}dt+{\gamma }_n{\Vert {\varphi }_t^v\cdot S_0^{\overleftrightarrow{n}}-S_1^{\overleftrightarrow{n}}\Vert }_{W\ast }^2+{\gamma }_{\kappa }{\Vert {\varphi }_1^v\cdot S_0^{\overleftrightarrow{\kappa }}-S_1^{\overleftrightarrow{\kappa }}\Vert }_{W\ast }^2}$$ (3)

Both weights γ_κ and γ_n control the contribution of each direction for the multidirectional varifolds matching. As for fibers, measuring a fiber f as a varifold refers to the mathematical operation of integrating a testing field ω_f along the fiber unoriented tangent vectors τ: f = ∫ ω_f(x)^tτ(x)dx.

2.2.2. Fiber-to-Surface Connectivity Features

For each triangular face ξ of the surface in the atlas ${\mathcal{A}}_i$, we determine from each training subject fibers that are connected to it after projection ${\pi }^{{\mathcal{A}}_i}({ℱ}_i)$ (Fig. 2A). The fibers connected to ξ are denoted as ${ℱ}_i(\xi )$ (Fig. 2B).

Figure 2. Key ingredients for prediction of non-diffeomorphic fiber development.

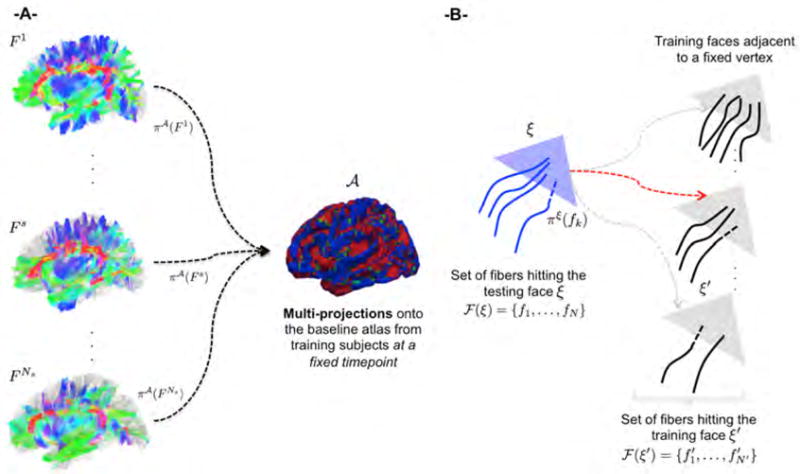
(A) Projections of fibers from training subjects {1, …, N_s} onto an atlas $\mathcal{A}$. The atlas stores for each face the set of fibers that are connected to it. (B) Using the proposed fiber-to-surface selection criterion to identify the triangular face ξ′ that is most similar to the triangular face ξ in the surface mesh of the training subject among the faces of surfaces of the training subjects.

We define a similarity between two triangular faces ξ and ξ′ with respectively $ℱ(\xi )=\{f_1,\dots ,f_{N_f}\}$ and $ℱ({\xi }^{\prime })=\{f_1^{\prime },\dots ,f_{N_f^{\prime }}^{\prime }\}$ as:

$$d(\xi ,{\xi }^{\prime })=d_{\mathrm{shape}}(\xi ,{\xi }^{\prime })+d_{\mathrm{termini}}(\xi ,{\xi }^{\prime })+d_{\mathrm{connectivity}}(\xi ,{\xi }^{\prime }).$$ (4)

The first term measures the overall shape representation difference between fibers connected to two triangular faces using the multidirectional varifold metric:

$$d_{\mathrm{shape}}(\xi ,{\xi }^{\prime })=\left|\frac{1}{N_f}{\displaystyle \sum _{k=1}^{N_f}{\Vert f_k\Vert }_{W\ast }-\frac{1}{N_f^{\prime }}{\displaystyle \sum _{j=1}^{N_f^{\prime }}{\Vert f_j^{\prime }\Vert }_{W\ast }}}\right|.$$ (5)

The second term quantifies the spatial closeness between the fiber termini positions

$$d_{\mathrm{termini}}(\xi ,{\xi }^{\prime })=\frac{1}{2}\left({\left|\frac{1}{N_f}{\displaystyle \sum _{k=1}^{N_f}{f}_k^1-\frac{1}{N_f^{\prime }}{\displaystyle \sum _{j=1}^{N_f^{\prime }}{f}_j^1}}\right|}_2+{\left|\frac{1}{N}{\displaystyle \sum _{k=1}^{N_f}{f}_k^2-\frac{1}{N_f^{\prime }}{\displaystyle \sum _{j=1}^{N_f^{\prime }}{f}_j^2}}\right|}_2\right),$$ (6)

where $f_k^1$ and $f_k^2$ are the two extremities of fiber f_k. The third term computes the difference between the number of fibers:

$$d_{\mathrm{connectivity}}(\xi ,{\xi }^{\prime })=\eta \left|N_f-N_f^{\prime }\right|,$$ (7)

where η is a tuning parameter.

2.2.3. Multishape Prediction Strategy

For surface prediction, we use the strategy described in Section 2.1. For fiber prediction, we first reconstruct using the training fibers a set of virtual fibers ${\stackrel{\sim }{ℱ}}_0$ that best resemble the baseline fibers ${ℱ}_0$ given by a testing subject. To achieve this, we project ${ℱ}_0$ onto the baseline cortical surface S₀ as well as onto the baseline atlas ${\mathcal{A}}_0$, hence estimating the subject-based and atlas-based connectivity features through fiber projections ${\pi }^{S_0}\left({ℱ}_0\right)$ and ${\pi }^{{\mathcal{A}}_0}\left({ℱ}_0\right)$.

For fiber projection on the inner cortical surface, we adopted the same strategy for fiber projection used in (Nie et al., 2014; Li et al., 2015). If the fiber extremity lies outside the cortical surface, the connection point is identified through a local search along the fiber backwards. Otherwise, the fiber is extended towards the inner cortical surface. The searching process stops either when the fiber hits the surface, or exceeds a searching threshold (20mm). Any fiber that cannot reach the surface is considered as an outlier and removed from the fiber tracts data.

Based on the connectivity features and the virtual shape ${\stackrel{\sim }{S}}_0$ described in Section 2.1.3, we update ${\stackrel{\sim }{ℱ}}_0$ so that it resembles ${ℱ}_0$. As previously stated, the construction of the virtual surface shape comprises moved and unmoved vertices in the baseline atlas. Hence, each triangular face ξ of the surface ${\stackrel{\sim }{S}}_0$ is associated with vertices that are either moved or not moved during the construction of the virtual shape. For each face ξ associated with unmoved vertex μ, the baseline atlas ${\mathcal{A}}_0$ well approximates the testing cortical shape. Hence, we use it as a proxy for fiber projections, where each of its faces stores the set of its connecting fibers from all training subjects (Fig. 2). Therefore, through simply exploring the set the connecting fibers from all training subjects to face ξ in ${\mathcal{A}}_0$, we can retrieve the set of training fibers that exhibit similar connectivity features to the testing fibers connected to the testing face ξ. Of note, once a triangular face on the baseline surface is explored, it is marked so it won’t be visited twice.

For a testing triangular face ξ that is associated with a moved vertex μ, we reconstruct its connecting fibers through selecting the face with the most similar fiber-to-surface connectivity features among the training faces adjacent to m-closest vertices to μ in the cloud $\mathcal{V}$. We then add the fibers of the selected training face to ${\stackrel{\sim }{ℱ}}_0$ and mark it. Ultimately, in both cases, for each selected training face with most similar fiber distribution to the testing face, we trace its diffeomorphic deformation using ϕ, while retrieving the set of its connecting fibers at different acquisition timepoints t_i, thereby jointly estimating the multishape development $({\stackrel{\sim }{S}}_i,{\stackrel{\sim }{F}}_i)$. Algorithm 1 summarizes the key steps involved in multishape prediction based on geometric, dynamic and connectivity features.

Algorithm 1.

Enhanced longitudinal multishape evolution prediction from baseline

1:	INPUTS: The longitudinal mean atlases ${\mathcal{A}}_i$, the set of training baseline vertices $\mathcal{V}$, the baseline testing multishape M0 = (S0; F0), and ${\pi }^{{\mathcal{A}}_0}(F_0)$.
2:	Initialize ${\stackrel{\sim }{S}}_i\leftarrow {\mathcal{A}}_i$ and ${\stackrel{\sim }{F}}_i=\left\{\right\}$ for i ∈ 2 {0; …; N}.
3:	Initialize ε as the mean distance between S0 and ${\mathcal{A}}_0$ plus its standard deviation.
4:	for every vertex μ in the reconstructed baseline shape ${\stackrel{\sim }{S}}_0$ do
5:	if its 3D position x is located outside the ε–neighborhood from S0 then
	Update x using surface topography-based selection criteria.
	* For each unchecked adjacent face ξ to μ, use the fiber-to-surface selection criterion to identify the most similar corresponding training face in fiber properties to the testing face. Mark this face as ‘checked’.
	* Retrieve the dynamic feature for μ as ${\stackrel{\sim }{S}}_i(x)=\varphi (x,t_i)$ at each timepoint.
	* Retrieve the spatiotemporal connectivity features for the selected deforming training face (set of fibers ${ℱ}_i(\varphi (\xi ,t_i))$ that hit $\varphi (\xi ,t_i)$ at timepoint, then ${\stackrel{\sim }{F}}_i={\stackrel{\sim }{F}}_i\cup {ℱ}_i(\varphi (\xi ,t_i))$.
6:	else
	Implement * while using projections of both training and testing fibers on their corresponding surfaces (no need to use the atlas for mutliprojections in this case).
7:	end if
8:	end for
9:	OUTPUT: Set of predicted multishapes $\left\{{\stackrel{\sim }{M}}_i=({\stackrel{\sim }{S}}_i,{\stackrel{\sim }{F}}_i)\right\}$ at timepoints ti.

3. Enhanced Framework for Prediction of Multishape Development

To further improve the prediction accuracy for cortical surfaces and fiber tracts, we propose two key variants.

3.1. Spatially Heterogeneous Construction of Virtual Shape Atlas

In constructing a virtual shape for prediction, we have used an empirical population-based mean atlas (Rekik et al., 2015b,a, 2016b). However, a population-based mean atlas generally captures only the ‘mean shape’ but not necessarily the details particular to the individual shapes of a testing subject. Alternatively, one can represent the testing shape by selecting the closest shape from among the training shapes (each considered as an atlas). We propose here to extend this idea by using multiple atlases to build a spatially heterogeneous atlas using the multidirectional varifold representation. This individualizes the atlas by locally maximizing its similarity to the testing baseline cortical shape for each cortical region, thereby resulting in a better representation.

The key idea is to compare the baseline testing surface locally with a distribution of atlases. For each anatomical cortical region of interest (ROI), we compute the pair-wise similarity between the testing ROI shape and an atlas ROI shape (Fig. 3). Generally, we define the similarity between two shapes S and S′ based on the inner-product (Rekik et al., 2016a):

$${\langle S,S^{\prime }\rangle }_{W\ast }=\frac{1}{2}{\displaystyle \sum _i{\displaystyle \sum _j{k}_e(c_i,c_j^{\prime })}}\frac{{\left(n_i^T{n}_j^{\prime }\right)}^2}{|n_i||n_j^{\prime }|}+\frac{1}{2}{\displaystyle \sum _i{\displaystyle \sum _j{k}_e(c_i,c_j^{\prime })}}\frac{{\left({\kappa }_i^T{\kappa }_j^{\prime }\right)}^2}{|{\kappa }_i||{\kappa }_j^{\prime }|}$$ (8)

Figure 3. Spatially heterogeneous atlas estimation using multidirectional varifold similarity metric.

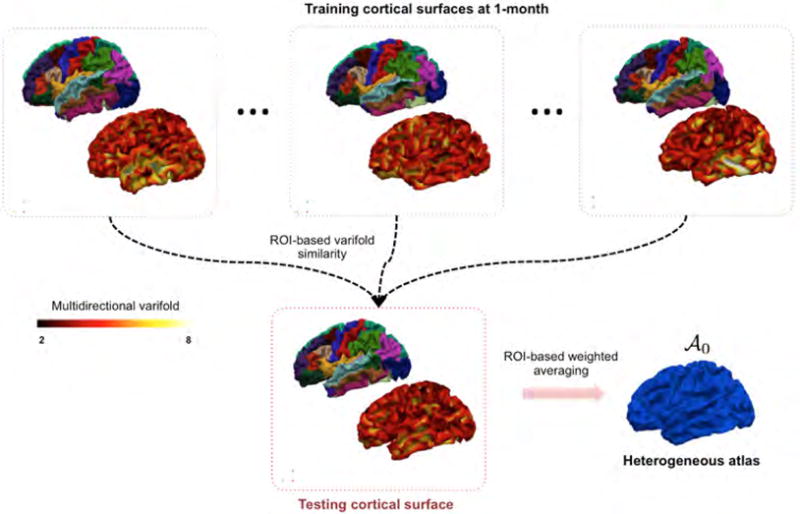
For each cortical region of interest (ROI), we perform a weighted averaging of vertices’s positions in different atlases (each training subject is regarded as an atlas). The weight assigned to each atlas is computed as the multidirectional varifold similarity value between the testing ROI and the atlas ROI.

To define the heterogenous atlas from multiple atlases, we perform a weighted averaging of all atlases for each ROI while using the multidirectional varifold similarity distance between the baseline shape and each of these atlas shapes as weight:

$${\mathcal{A}}_{\mathrm{heterogenous}}=\frac{{\displaystyle {\sum }_{l=1}^{N_l}{\displaystyle {\sum }_{j=1}^{N_{tr}}{w}_{j,l}{\mathcal{A}}^j({\mu }_l)}}}{{\displaystyle {\sum }_{l=1}^{N_l}{\displaystyle {\sum }_{j=1}^{N_{tr}}{w}_{j,l}}}},$$ (9)

where μ_l is a vertex belonging to the l-th ROI, N_l denotes the number of labeled cortical regions, ${\mathcal{A}}^j$ denotes the j-th atlas, N_tr represents the number of training subjects (or atlases) and w_j,l denotes the multidirectional varifold similarity between the testing shape S₀ and the atlas ${\mathcal{A}}^j$ in the l-th cortical ROI. Subsequently, the estimation of a series of spatiotemporal heterogeneous atlases is straightforward. We simply apply the same weighted averaging strategy to the corresponding atlases at each time point.

3.2. Temporally-Consistent Connectivity Features Using Low-Rank Tensor Completion

Fiber projection patterns can be highly variable across time points, as shown in Fig. 1. To address this issue and further refine the fiber selection criterion, we enforce temporal consistency of the connectivity distances d_connectivity computed across time points. Basically, we aim to obtain quite reliable estimates of the scalar fiber connectivity features (here fiber hits per face) at later timepoints from neonatal fiber connectivity features. This yields to defining the temporally consistent connectivity distance between a testing face ξ and a training face ξ′ (as in Fig. 2):

$$d_{\mathrm{connectivity}}(\xi ,{\xi }^{\prime })=\eta \left(\left|N_f(t_0)-N_f^{\prime }(t_0)\right|+{\displaystyle \sum _{i=1}^N\left|{\stackrel{\sim }{N}}_f(t_i)-N_f^{\prime }(t_i)\right|}\right)$$ (10)

where Ñ_f(t_i) denotes the estimated number of the fibers hitting the testing face ξ at timepoint t_i and N_f(t₀) is the number of ground-truth fibers hitting the testing face ξ at the baseline timepoint t₀. $N_f^{\prime }(t_i)$ represents the observed number of fibers hitting the training face ξ′ at timepoint t_i.

To estimate the missing scalar connectivity feature values {Ñ_f(t_i)}, i ∈ [1, …, N], we formulate the problem as a low-rank tensor completion problem as illustrated in Fig. 4. Intuitively, one can assume that at a specific timepoint and a specific location, we can linearly represent the connectivity features of a testing subject using the connectivity features of other training subjects as developing brains share many similar growth profiles (Li et al., 2015; Nie et al., 2014). This can also be applied to neighboring vertices in the spatial or time domains, where their relationship can be thought of as ‘locally dependent’. Hence, at each vertex μ of the testing cortical surface, we define a tensor ${\mathcal{T}}_{\mu }$ of size N_k×N_t×N_s, where N_k denotes the k—ring neighboring faces to vertex μ, N_t represents the number of acquisition timepoints (including the first observation), and N_s the number of subjects (including the testing one). Next, we define a masking tensor ${ℰ}_{\mu }$ of the same size, where we assign 0 values to unknown connectivity features to estimate for the testing subject at later timepoints and 1 for the known testing and training connectivity features (Fig. 4–B). To complete the missing values of the tensor product ${\mathcal{T}}_{\mu }{ℰ}_{\mu }$, we use the recently developed low-rank tensor completion method (Kressner et al., 2014), where tensors are embedded onto a smooth manifold ${ℳ}_{\mathrm{r}}$ with a multilinear rank r. After properly projecting the incomplete tensor on the manifold of low-rank tensors ${ℳ}_{\mathbf{r}}$, it is completed through minimizing the Riemannian gradient of the following objective function:

$$\{\begin{array}{l}{min}_{{\stackrel{\sim }{T}}_{\mu }}f({\stackrel{\sim }{T}}_{\mu })=\frac{1}{2}{\Vert P_{\mathrm{\Omega }}{\stackrel{\sim }{T}}_{\mu }-P_{\mathrm{\Omega }}{\mathcal{T}}_{\mu }{\mathrm{ℰ}}_{\mu }\Vert }^2\hfill \\ \mathit{subject}\mathit{to}{\stackrel{\sim }{T}}_{\mu }\in {ℳ}_{\mathrm{r}},\mathit{rank}\left({\stackrel{\sim }{T}}_{\mu }\right)=\mathrm{r}\hfill \end{array}$$ (11)

with ${\stackrel{\sim }{T}}_{\mu }$ denoting the completed tensor and P_Ω representing the projection on a sampling set Ω.

Figure 4. Mean-guided low-rank tensor completion.

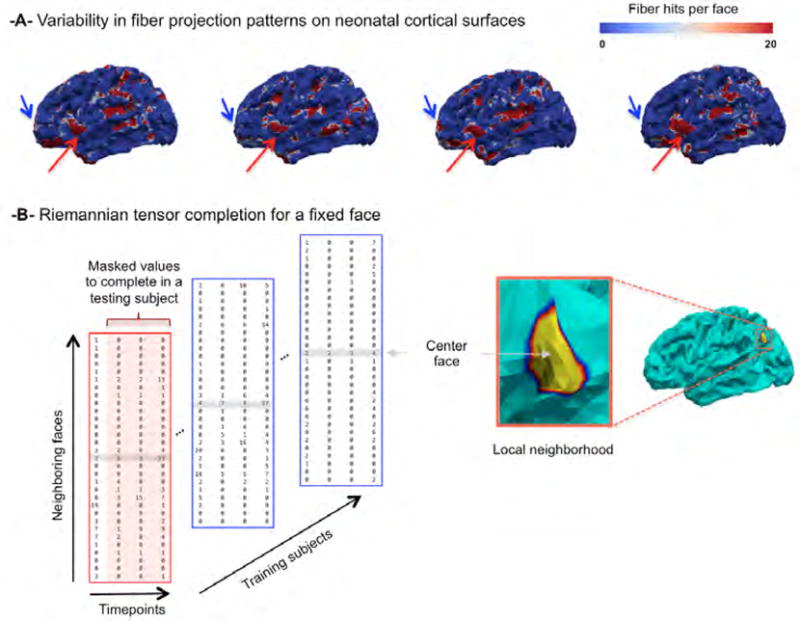
(A) The top row illustrates the variability in fiber projection patterns on neonatal cortical atlas from four training subjects. (B) Illustration of the incomplete tensor centered at a fixed face on the cortical surface.

• Mean-guided low-rank tensor completion. To further boost up the performance of the conventional framework proposed in (Kressner et al., 2014) and since our data (i.e. connectivity features) may be noisy, we propose in this work to use a confidence map that retains the temporally-consistent connectivity features across multiple timepoints (Li et al., 2015; Nie et al., 2014). In our case, we simply estimate the confidence map through computing, at each vertex on the spatiotemporal heterogeneous atlas, the mean of the training feature connectivity maps over time. Then, for testing faces with high values in the confidence map where the connectivity pattern seem to be temporally least variable, we use tensor completion. Otherwise, we directly assign the mean values in the confidence map to the missing values in the tensor ${\stackrel{\sim }{T}}_{\mu }$. Practically, we update ${\stackrel{\sim }{E}}_{\mu }$ such that it takes zeros at the ‘confident’ missing values, whereas the ‘noisy’ ones are replaced with the mean values in the original complete tensor T_μ, then we solve Eq. 11 as detailed in (Kressner et al., 2014).

• Averaging overlapping predicted connectivity features. Ultimately, after solving the tensor completion problem at each vertex of a testing shape, we predict the missing connectivity feature value at the center face of the k−ring neighborhood to each vertex μ of the baseline surface S₀ as illustrated in Fig. 4. However, noting that a face will be included in different local neighborhoods, we estimate its final connectivity feature value through locally averaging its predicted values within different neighbouring tensors.

4. Results

4.1. Dataset and parameter setting

We use leave-one-out cross-validation to evaluate the proposed framework using data of 10 left and right cortical hemispheres from 5 infants, each with longitudinal diffusion and structural MR images acquired at around birth, 3, 6, and 9 months of age. For varifold surface and fiber representation, we set σ_W = 5 for the shape kernel K_W, σ_V = 30 for the deformation kernel K_V, and γ_n = γ_κ = 0.001 for the energy E as explained in (Rekik et al., 2015a, 2016a). Streamline tractography (Stieltjes et al., 2001) was used to estimate the fibers inside each cortical surface at each timepoint. For atlas individualization, we fixed the parameter ε as the mean distance between S₀ and ${\mathcal{A}}_0$ minus its standard deviation, and chose m = 25 as the number of the closest neighbors to use for local morphing. For tensor completion, we performed a grid search to fix the multilinear rank r = [4, 3, 2], for respectively the spatial neighborhood dependency the temporal neighborhood dependency and the training samples dependency. For the face neighborhood ring, we selected k = 3, which involves 31 neighbors. A face in the mean connectivity cortical map is considered as belonging to a ‘confident region’, if its connectivity value is higher than the average of the non-zero mean connectivity coritcal values minus their standard deviation. For the face-to-face distance using fiber properties, η = 0.01.

Image processing

All MR images at all the acquisition timepoints were preprocessed using a standard framework developed in (Dai et al., 2013; Li et al., 2014) including (1) the removal of the skull (Shi et al., 2012), followed by the removal of the cerebellum and brain stem by registering an atlas to each subject (Shen and Davatzikos, 2002; Wu et al., 2006); (2) intensity inhomogeneity correction using N3 method (Sled et al., 1998); (3) rigid alignment of each image to the age-specific infant brain atlas (Shi et al., 2011); (4) longitudinal infant tissue segmentation of infant brain MR images into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF): since MR images around 6 months of age are very challenging to segment, we first adopted a state-of-the-art learning-based method (Wang et al., 2011, 2014; Zhang et al., 2015) that leverages random forests and multimodal appearance features and context features from T1w, Tw2 and FA images, to generate the preliminary segmentation results for each image. To improve accuracy and longitudinal consistency, we further refined the segmentation results using a 4D level-set method (Wang et al., 2013); and (5) filling the cortex insides and splitting the brain into left and right hemispheres.

Cortical surface reconstruction

For each segmented image, we reconstructed the inner cortical surface for each hemisphere using a deformable surface method (Li et al., 2012). In particular, we corrected the topological defects in the WM and tesselated the cortical surface as a triangular mesh to guarantee a spherical topology for each hemisphere as proposed in (Li et al., 2012, 2014). Ultimately, each cortical hemisphere was parcellated using the robust framework developed in (Li et al., 2014).

Diffusion tensor imaging processing and tractography

The imaging parameters for diffusion weighted images (with 60 axial slices) are as follows: TR/TE = 7680/82ms, matrix size = 128 × 96, 42 noncollinear diffusion gradients, and diffusion weighting b = 1000s/mm². We used FSL tools for eddy current and distortion correction for DWI sequence. Then, we constructed diffusion tensors by a weighted least squares estimation method and computed the fractional anisotropy (FA) map. Next, for each subject, we affinely aligned structural T2 image with b0 image based on mutual information. The generated transformation matrix applied to cortical surfaces to transfer them onto the DTI space as in (Li et al., 2015). At last, within the mask of each hemisphere, we performed deterministic streamline tractography (Yap et al., 2011) on each DTI image in its native space with a minimal seed point FA of 0.2, minimal FA value of 0.1, a maximal turning angle of 45°, and minimal fiber length of 25mm. We used low FA threshold to ensure that unmyelinated white matter fibers could be reasonably extracted in infant brains.

4.2. Evaluation metrics

For surface evaluation, we use both Dice index, which quantifies the face-to-face cortical overlap between two surfaces S and S′ as the ratio $\frac{2A(S\cap S^{\prime })}{A(S)+A(S)}$ (Li et al., 2009), and the symmetric Euclidean distance. A(·) denotes the area of the surface, and the ∩ operator takes the intersection of the two surfaces. Of note, A(S) is computed by summing up each vertex’s area, which we define as the average area of all faces that contain this vertex. For fiber prediction evaluation, we introduce three metrics: (1) Global mismatch (%). This represents the percentage of faces with attached fibers while the corresponding predicted faces had no fibers and vice versa. (2) Fiber mismatch per face. This metric represents the average number of mismatched fibers per face across surface faces that are hit by either predicted or ground truth fibers or both. (3) Mean whole-brain varifold difference. For a pair of faces both with traversing fibers, we use the unidirectional varifold metric to measure a face-wise discrepancy between the ground truth and predicted fibers F and $\stackrel{\sim }{F}$ connected to two surfaces S and $\stackrel{\sim }{S}$: $\frac{1}{N_{\xi }}{\displaystyle {\sum }_{i=1}^{N_{\xi }}|{\Vert F^{{\xi }_i}\Vert }_{W\ast }-{\Vert {\stackrel{\sim }{F}}^{{\xi }_i}\Vert }_{W\ast }|}$, with N_ξ denoting the number of faces in S, and ξ_i a face in S.

4.3. Multishape prediction results and evaluation of variants

Despite the small size of our dataset and its large variability in cortical shape and fiber tracts, our framework led to very promising results as will be further detailed. Fig. 5 shows a good overall overlap between ground truth and predicted multishape for a representative testing subject at 3, 6 and 9 months.

Figure 5. Proposed multishape prediction for a representative subject.

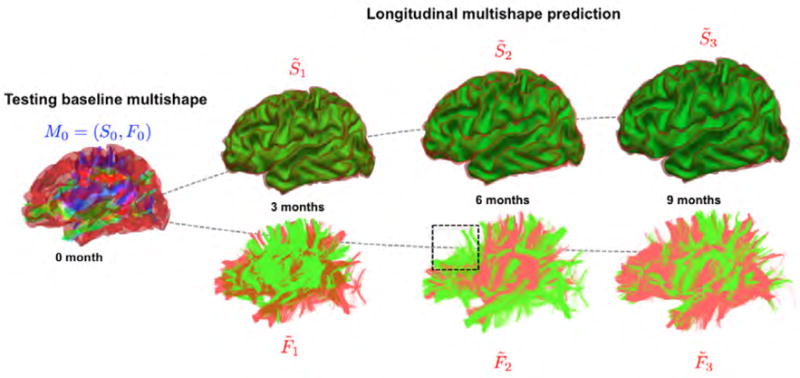
The red multishape represents the ground truth while the one in green represents the predicted multishape. The dashed blue box locates a region where the lack of spatiotemporal consistency in fiber tractography across different timepoints is obvious, which makes the prediction task more challenging since it is based on the training spatiotemporal tracts. We notice a very good prediction of the cortical shape and an overall satisfactory prediction of the diffusion fibers.

Evaluation of the heterogeneous atlas variant for cortical shape prediction

To assess the advantage of the proposed spatially heterogeneous atlas reconstruction over using conventional atlas reconstruction methods, we evaluated the cortical surface prediction accuracy in terms of mean Dice index and mean symmetric Euclidean distance between the ground truth shape and the predicted shape at later acquisition timepoints in the following cases: (a) selecting the best representative baseline atlas from the training subjects that is most geometrically similar to the baseline testing shape using the symmetric Euclidean distance, (b) selecting the best representative baseline atlas from the training subjects that is most morphologically similar to the baseline testing shape using the multidirectional varifold metric, and (c) estimating the spatially heterogeneous atlas while using as a similarity metric the symmetric Euclidean distance. As noted in Tables 2 and 3, the proposed approach significantly (p < 0.05) outperformed the baseline method (using one atlas and Euclidean distance as a metric) at all missing timepoints. This shows that the multidirectional varifold distance better individualizes the atlas to make it more locally similar in morphology to the testing cortical surface than the conventional symmetric Euclidean distance. When compared with the proposed varifold one-atlas and the Euclidean heterogeneous atlas, we notice a slight improvement in prediction accuracy.

Table 2. Surface prediction accuracy evaluation using Dice index averaged across 10 cortical hemispheres.

Our method (in bold) outperformed each of the three baselines with statistical significance

	3 months	6 months	9 months
Euclidean one-atlas	86.15	80.58	75.45
Varifold one-atlas	89.29	81.67	76.03
Euclidean heterogeneous-atlas	89.33	81.95	76.28
Varifold heterogeneous-atlas	90.12*	82.48*	76.83*

^*p < 0.05.

Table 3. Surface prediction accuracy evaluation using symmetric Euclidean distance (mm) averaged across 10 cortical hemispheres.

Our method (in bold) outperformed each of the three baselines with statistical significance

	3 months	6 months	9 months
Euclidean one-atlas	1.24	1.33	1.70
Varifold one-atlas	0.79	1.04	1.27
Euclidean heterogeneous-atlas	0.78	1.02	1.25
Varifold heterogeneous-atlas	0.77*	1.01*	1.24*

^*p < 0.05.

Additionally, we locally evaluated the accuracy of our prediction method in 35 anatomical cortical regions averaged across left and right hemispheres (Fig. 6), which showed a spatially-varying prediction accuracy that generally decreased with time. These regionally non-uniform error maps are most likely caused by the spatial inter-subject variabilities in terms of cortical folding and development. Nonetheless, our prediction accuracy still fitted into a promising range of prediction values for each evaluation metric. For the cortical surface, when using the Dice index to evaluate the anatomical alignment between the ground-truth and the predicted surfaces, the prediction mainly dropped in certain cortical areas such as the bank of the superior temporal sulcal and the middle temporal gyrus. As for the Euclidean symmetric distance, it also increased in the middle temporal gyrus as well as the buried highly folded insula cortex. Notably, the mean prediction error gradually increases as the shape to predict becomes very distant in time from the baseline surface. Additionally, the proposed mutlidirectional varifold-based heterogeneous atlas outperformed the baseline Euclidean one-atlas in the majority of cortical regions, particularly in the posterior cingulate cortex, the precentral gyrus, the insula cortex and the medial orbito-frontal cortex.

Figure 6. Prediction accuracy evaluation in 35 anatomical ROIs using the baseline Euclidean one-atlas and the proposed mutltidirectional varifold-based heterogeneous atlas estimation averaged across both right and left hemispheres.

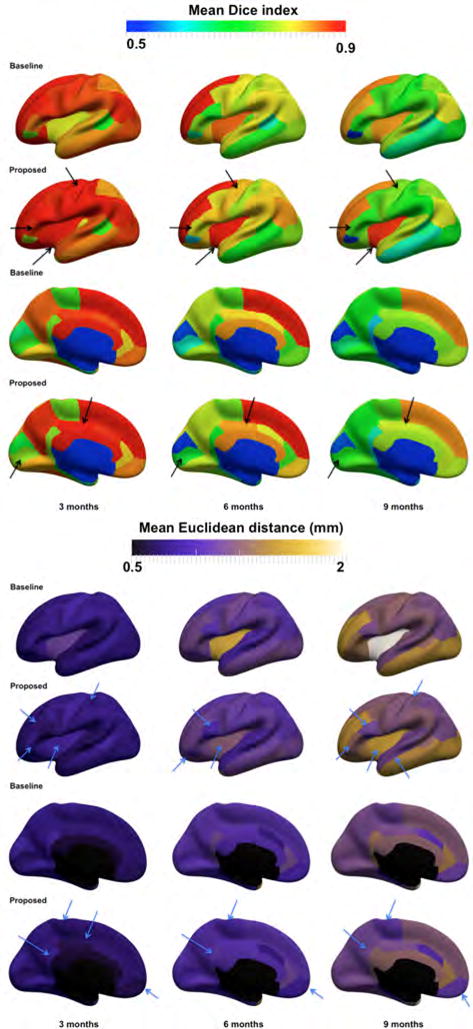
(Top) Mean Dice index between the ground truth and the predicted surfaces, averaged in each of the 35 anatomical ROIs, across 10 hemispheres from 5 infants. (Bottom) Mean vertex-wise surface distance error between the ground truth and the predicted surfaces, averaged in each of the 35 ROIs, across 10 hemispheres from 5 infants. The arrow points to a few of the anatomical regions where the proposed method visibly outperformed the baseline method.

Evaluation of the temporally-consistent fiber selection criterion using mean-guided tensor completion

The proposed mean-guided tensor completion strategy gave reliable improvement over the baseline method (Kressner et al., 2014) as shown in Table 4. We also display in Table 5 the fiber prediction accuracy using the three proposed evaluation metrics. The proposed temporal consistency constraint for face selection in the fiber prediction strategy helped improve the fiber prediction results for all evaluation metrics and at all missing timepoints when compared to the original strategy proposed in ((Rekik et al., 2016b)) –except for the global fiber mismatch at 9 months.

Table 4.

The absolute mean difference between the estimated missing connectivity features and the ground-truth connectivity features using the conventional low-tensor completion method (Kressner et al., 2014) and the refined one using the mean connectivity feature confidence map.

	3 months	6 months	9 months
Estimation error ((Kressner et al., 2014))	1.70	2.85	2.86
Estimation error (with mean guidance)	1.64	2.70	2.70

Table 5.

Fiber prediction accuracy evaluation averaged across 10 cortical hemispheres.

	3 months	6 months	9 months
global mismatch % (Rekik et al., 2016b)	20.80	19.60	19.25*
global mismatch % (Proposed)	19.8	19.4	20.00
fiber mismatch per face (Rekik et al., 2016b)	3.11	2.78	3.13
fiber mismatch per face (Proposed)	2.60*	2.37*	3.04
mean whole-brain varifold distance (Rekik et al., 2016b)	32.30	32.29	34.82
mean whole-brain varifold distance (Proposed)	32.22	29.74*	33.17

^*denotes statistically significant results (p < 0.05) when compared to baseline methods.

On a local level, we plot in Figures 7 and 8 the fiber mismatch per face as well as the global mismatch for each ROI between the ground truth and the predicted fiber tracts. The proposed variant outperformed the baseline method (Rekik et al., 2016b) in 88.57% of the ROIs at 3 months, 85.71% at 6 months, and 68.57% at 9 months in terms of the average fiber mismatch per face. We also notice a similar global trend in mean fiber mismatch per face distribution across the three prediction timepoints. For instance, we notice that the mismatch error peaks in the insula cortex (which is a highly folded large region deeply buried in the cortical surface) and the temporal pole (which is a very small cortical region) in Figure 7. As for the global fiber mismatch, it decreases the prediction error in respectively 88.57% of the cortical regions at 3 months, 85.71% at 6 months, and 68.57% at 9 months. Interestingly, in addition to the rostral anterior cingulate cortex and the posterior cingulate cortex, the global fiber mismatch error peaks in the same cortical regions as for the mean fiber mismatch per face (i.e, the insula cortex and the temporal pole) (Figure 8). A closer look at Figure 8 also reveals more consistent error distribution patterns at 6 and 9 months compared with 3 months. This may be explained by the similar fiber surface connectivity patterns between 6 and 9 months compared to an earlier developmental timepoint (3 months).

Figure 7. Mean fiber mismatch per face across 10 hemispheres in 35 cortical regions of interest (ROIs).

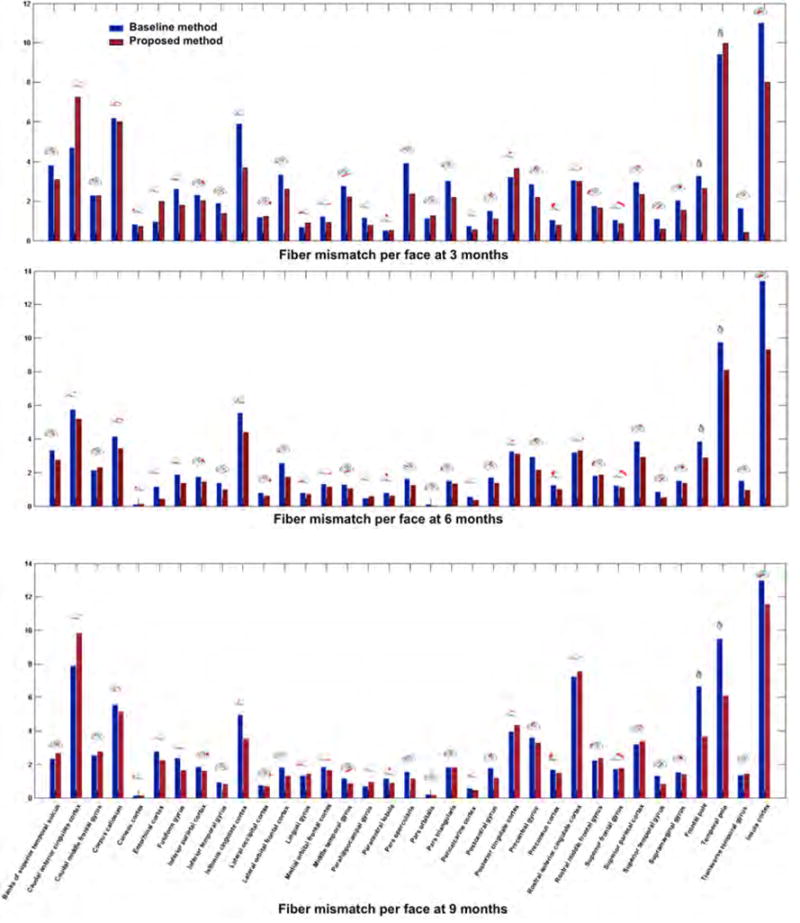
We plot the proposed mean fiber prediction mismatch per face against the baseline fiber prediction strategy introduced in (Rekik et al., 2016b). The proposed method, which integrated the estimated spatiotemporal connectivity features using the mean-guided low-tank tensor completion method into the fiber selection criteria, decreased the fiber mismatch (or at least had a similar mismatch) in 88.57% of the ROIs at 3 months, 85.71% at 6 months, and 68.57% at 9 months.

Figure 8. Mean fiber global mismatch across 10 hemispheres in 35 cortical regions of interest (ROIs).

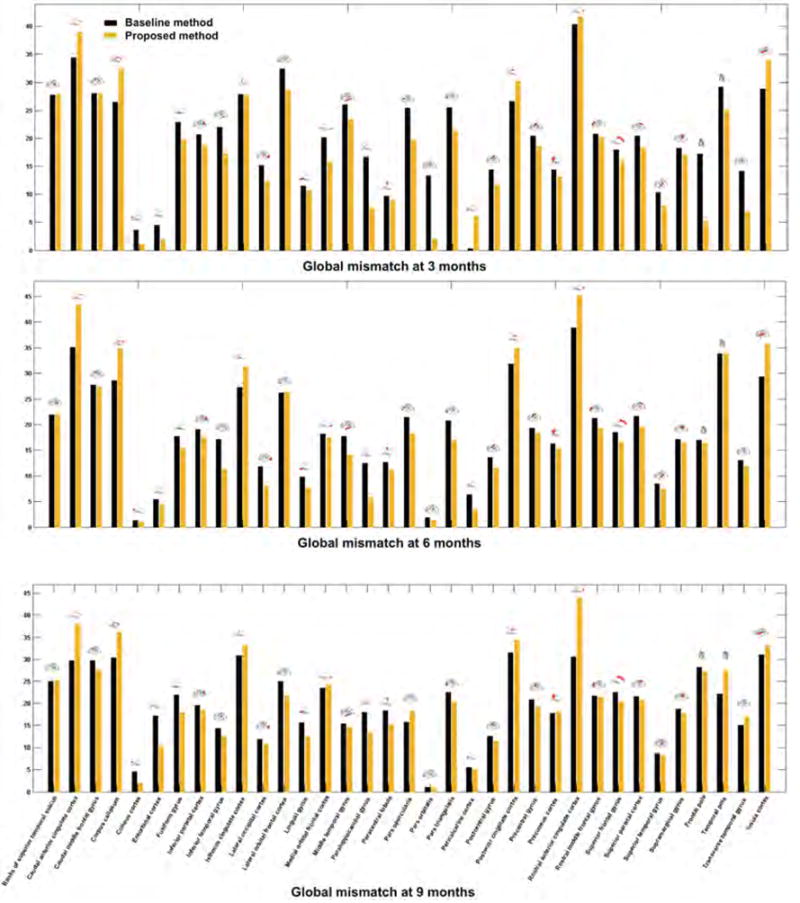
We plot the proposed mean fiber prediction mismatch per face against the baseline fiber prediction strategy introduced in (Rekik et al., 2016b). The proposed method, which integrated the estimated spatiotemporal connectivity features using the mean-guided low-tank tensor completion method into the fiber selection criteria, decreased the fiber mismatch (or at least had a similar global mismatch) in 80% of the ROIs at 3 months, 77.14% at 6 and 9 months.

5. Discussion

We presented the first heterogeneous atlas-based multishape prediction framework with temporally-consistent fiber selection strategy that predicts both the diffeomorphic dynamic cortical surface and non-diffeomorphic fiber tracts growth in infants during the first 9 months of postnatal development, solely from the baseline multishape at birth. We used the diffeomeorphic multidirectional varifold-based cortical surface shape regression model to learn both geometric and dynamic features of cortical surface shape growth for shape prediction at later timepoints. In addition, we used multiprojections from fibers of training subjects onto the heterogeneous atlas to extract the fiber-to-face connectivity features to guide fiber prediction. Although the infant multishape is both challenging on the cortical surface level with its highly convoluted foldings and dynamic growth and on the diffusion fiber tracts level with their dramatic change in topology due to myelination (Verma et al., 2005), the proposed framework showed promising prediction results, particularly when compared with the baseline method proposed in (Rekik et al., 2016b). Furthermore, we note that our results showed that heterogeneous atlases, estimated from many samples of the population, are better at predicting the developmental trajectory of a testing multishape, in comparison to using a single most similar training subject (i.e., one-atlas). This indicates that infant brains at birth are more likely to follow the individualized population trajectory (i.e, heterogeneous atlas), rather than following the trajectory of the most similar subject in multishape (a single atlas).

We would like to note that the proposed multishape learning framework is generic and can also be applied to any longitudinal multishape estimated from structural and diffusion data.

However, there are several limitations to this study that would lead to a much better performance of the proposed multishape prediction framework when conveniently addressed. First, as pointed out in (Reveley et al., 2015), subject-specific long-range tractography over a hemisphere poses severe challenges. Even a more challenging task would be to develop a non-diffeomorphic longitudinally consistent brain tractography algorithm as a preprocessing step, which may contribute into improving the fiber selection strategy (Figure 5). To the best of our knowledge, such method has not been tailored yet to handle with high accuracy developing 3D fiber tracts. Also, there is a decrease in tractography accuracy when the fibers approach the cortical surface. Second, using a larger longitudinal infant dataset with both structural and diffusion data would generate a better heterogeneous atlases as more atlases will capture a larger spectrum of shape variation. This also will engender a denser pool of training connectivity features for better feature selection. Besides, we did not examine the sensitivity of a few parameters, such the number of the closest vertices m and the face neighborhood ring size k, because of the small training sample size. So we just estimated them empirically using inner leave-one-out cross-validation on the training set. With a much larger training sample size, we can better examine these parameters in our method and estimate their impacts on the prediction accuracy. Third, there is a large variability in fiber hits on the cortical surface that may be better captured when increasing the number of samples as well as the number of acquisition timepoints. This would also improve the low-rank tensor completion problem through balancing the dimensions of the tensor. Fourth, as there is no conventional method to average developing fiber tracts across different timepoints, we used fiber projections on the cortex to somehow establish spatiotemporal correspondence between fibers. This strategy can be further improved through projecting not only the fiber termini on the surface but other fiber properties (such as the shape and length). This can be envisioned as multi-layer coloring of the atlas with different complementary scalar fields to guide the multishape prediction process. Fifth, many samples were excluded since they had missing diffusion MRI data at some timepoints or corrupted data. Addressing the problem of unbalanced multishape data and a varying number of acquisition timepoints, which was highlighted as one of the challenging issues in longitudinal data in (Gerig et al., 2016), would propel the generalizability of our method. Last, the proposed model is only able to predict fiber tracts that hit the cortical surface.

For the model parameters ε-proximility and m-closest neighbors, these were proposed to select from the cloud the most locally similar individual cortical shapes for prediction. This is in line with the concept of ‘atlas individualization’, where in the neuroscience literature it was noted that the human brain have some ‘shared’ similar traits across subjects (population-based or atlas-based), but also ‘individual’ traits (individual-based) (Wang et al., 2015). We adopt a similar way of reasoning where we first initialize the cortical surface using the population average (or atlas), then locally individualize it through selection of the most similar individual points from the cloud to our subject. The underlying assumption of this local morphing strategy is that the most similar shapes will most likely have similar developmental trajectories. This hypothesis has been tested in our preliminary work on cortical shape prediction on 24 cortical surfaces (Rekik et al., 2015a,b). We would also like to point out that for the second variant, one could have used other regression/mapping methods to estimate the missing connectivity features such as the regression random forest (Meng et al., 2016). However, we believe that there are more parameters to tune for the regression random forest such as the number of trees and the tree depth. Additionally, other shape models can be used to build the developmental trajectories of multishapes in the training stage such as the non-linear mixed-effects modeling reviewed in (Gerig et al., 2016).

A subsequent implication of developing such predictive models may include in future applications the prediction of brain anatomical networks in early human brain development (Fan et al., 2011; Brown et al., 2014) and even children and adoslecents (Khundrakpam et al., 2016). Ultimately, this model can serve as a stepping stone to develop more ‘holistic’ brain development prediction models that include cognition such in (Erus et al., 2015) and functional connectivity such in (Smyser et al., 2016). One could also use this model to learn and predict developmental trajectories of extremely preterm infants (Padilla et al., 2015; Rimol et al., 2016). Furthermore, noting the heritability of the brain neuroanatomical shape (Ge et al., 2015), we can further include genetic features to guide the multishape development predictive model. Additionally, recent studies have shown that the shape of subcortical brain regions and cortical folding patterns provide information not available in volumetric measurements that is predictive of disease status, onset and progression in schizophrenia, autism, bipolar disorder, Alzheimer’s disease, and other mental disorders. There is also increasing evidence that genetic variants may have influences on brain morphology that can be captured by shape measurements (Ge et al., 2015; Rekik et al., 2016b). For instance, the development and aging of cortical thickness was shown to correspond to genetic organization patterns in (Fjell et al., 2015). Hence, learning to accurately predict longitudinal changes in brain multishapes would be of great clinical interest and will exhibit a nascent ability to learn more challenging shape evolution models, such as functional shapes (Charlier et al., 2014). Last, in our prediction framework, we assumed that the evolution of multishape at a vertex (or in an ROI) is independent of that at a remote vertex (or in other ROIs). However, this may not be the case in many developmental brain disorders, where patients do not display an impairment of focal growth but rather multi-regional impairment through cortico-cortical networks. Thus, integrating a longitudinal regional connectivity covariance into the proposed multishape evolution prediction framework may improve the prediction performance, particularly for clinically implicated infants.

6. Conclusions

Very few models exist on predicting shape development, especially in infants. This is a recently emerging field with high-level meaningful implications in medicine and healthcare. We presented in this work the first generalization of the developing shape prediction model to multishape, which include cortical surfaces and diffusion fiber tracts. The proposed multishape prediction framework can be further tailored to examine and predict development, ageing, disease/disorder progression, recovery after treatment or a therapeutic intervention, without the need to further acquire subject-specific longitudinal imaging (using a single measurement in time). Eventually, we envision to build models that not only capture and predict time-varying anatomy but also time-varying function and cognition.