Figure 4.
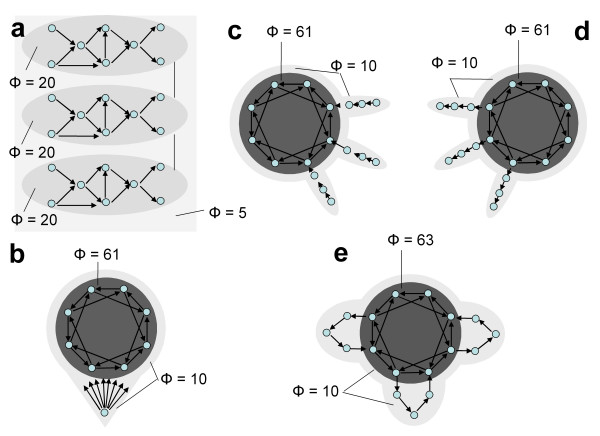
Information integration and complexes for other neural-like architectures. a. Schematic of a cerebellum-like organization. Shown are three modules of eight elements each, with many feed forward and lateral connections within each module but minimal connections among them. The analysis of complexes reveals three separate complexes with low values of Φ (Φ = 20 bits). There is also a large complex encompassing all the elements, but its Φ value is extremely low (Φ = 5 bits). b. Schematic of the organization of a reticular activating system. Shown is a single subcortical "reticular" element providing common input to the eight elements of a thalamocortical-like main complex (both specialized and integrated, Φ = 61 bits). Despite the diffuse projections from the reticular element on the main complex, the complex comprising all 9 elements has a much lower value of Φ (Φ = 10 bits). c. Schematic of the organization of afferent pathways. Shown are three short chains that stand for afferent pathways. Each chain connects to a port-in of a main complex having a high value of Φ (61 bits) that is thalamocortical-like (both specialized and integrated). Note that the afferent pathways and the elements of the main complex together constitute a large complex, but its Φ value is low (Φ = 10 bits). Thus, elements in afferent pathways can affect the main complex without belonging to it. d. Schematic of the organization of efferent pathways. Shown are three short chains that stand for efferent pathways. Each chain receives a connection from a port-out of the thalamocortical-like main complex. Also in this case, the efferent pathways and the elements of the main complex together constitute a large complex, but its Φ value is low (Φ = 10 bits). e. Schematic of the organization of cortico-subcortico-cortical loops. Shown are three short chains that stand for cortico-subcortico-cortical loops, which are connected to the main complex at both ports-in and ports-out. Again, the subcortical loops and the elements of the main complex together constitute a large complex, but its Φ value is low (Φ = 10 bits). Thus, elements in loops connected to the main complex can affect it without belonging to it. Note, however, that the addition of these three loops slightly increased the Φ value of the main complex (from Φ = 61 to Φ = 63 bits) by providing additional pathways for interactions among its elements.
