Skip to main content
PMC home page
Royal Society of Chemistry logoLink to Royal Society of Chemistry
. 2017 Mar 14;19(13):9028–9038. doi: 10.1039/c7cp00982h

On the relation between carbonyl stretching frequencies and the donor power of chelating diphosphines in nickel dicarbonyl complexes†

Marco Fusè a,✉, Isabella Rimoldi b, Edoardo Cesarotti b, Sergio Rampino a,✉, Vincenzo Barone a
PMCID: PMC5436090  PMID: 28304027

graphic file with name c7cp00982h-ga.jpgWe unravel the mechanisms of chelation-bond formation in nickel dicarbonyl complexes with bidentate phosphines and demonstrate that σ donation drives the carbonyl stretching response to the metal–ligand bond formation.

Abstract

The relation between spectroscopic observables and the detailed metal–ligand bonding features in chelation complexes is addressed using both experimental and state-of-the-art theoretical and computational methods. We synthesized and characterized a set of six nickel dicarbonyl complexes of general formula [Ni(CO)2(PP)], where PP is an atropoisomeric chelating diphosphine ligand. The analysis of the obtained experimental data and the basicity and oxidative potentials of the free ligands suggests a close relation between the donor ability of the chelating ligand and the carbonyl stretching frequencies observed in the complexes. We then use theory to unravel the detailed mechanisms of chelation-bond formation in terms of partial charge flows between the molecular orbitals of the fragments. By extending the promising, recently published natural orbitals for chemical valence/charge displacement (NOCV/CD) analysis scheme we provide a thorough, quantitative description of the several charge fluxes following the metal–ligand bond formation and demonstrate that the carbonyl stretching frequencies in the considered complexes selectively respond to the σ-donation charge flow from the phosphorus lone pairs of the ligands, with the frequency shift being in quantitative correlation with the extent of the ligand-to-metal charge transfer.

1. Introduction

In homogeneous catalysis, bidentate phosphines are a successful and widely used class of ligands which have proved their worth over many decades.1 After coordination at the metal center, the chelating structure is able to impose a relatively rigid environment, tuning the electron richness of the metal and, in turn, the reactivity of the coordinated complex. For these reasons, understanding the properties of the metal–ligand chemical bond is of fundamental importance for rationalizing and predicting the catalytic efficiency of these complexes and for developing new catalysts.

As far as monophosphines are concerned, the most widely used experimental probe of the electronic effects of phosphine ligands at the metal center is Tolman's electronic parameter (TEP).2,3 TEP is based on the position of the A 1 carbonyl stretching-frequency band in the spectrum of [Ni(CO)3L], where L is a phosphine ligand, with respect to the stretching vibration of free CO as recorded in the gas phase, which has a value of 2143 cm–1.4 In classical mononuclear carbonyl complexes, the A 1 carbonyl stretching frequency lies in the range 2125–1850 cm–1,5 and the observed red shift with respect to free CO is taken as a measure of the overall donor ability of L. Though the validity of such approach has been recently questioned (see for instance ref. 6, where evidence is given for intramolecular interactions interfering with the carbonyl stretching response to the ligand–metal interaction) and alternative, more sophisticated parameters have been proposed,7 TEP still represents a traditional and widespread method for assessing and comparing the electronic properties of the ligands.8 Unfortunately, TEP provides no information on the detailed features of the metal–ligand bond in terms of its Dewar–Chatt–Duncanson σ donation and π back-donation components. To this purpose, several theoretical studies, mainly in the framework of density functional theory (DFT), have been reported in the last few decades (see for example ref. 9–13). These are based on a number of successful bond-analysis schemes such as natural bond orbitals (NBO), charge-decomposition analysis (CDA), energy-decomposition analysis (EDA) and atoms in molecules (AIM).

As for bidentate phosphines, a parameter which has been so far widely used to predict the reactivity of diphosphine complexes is the bite angle (β),14,15 defined as the P–M–P angle. It is worth noting here that the bite angle, however, accounts for both a steric effect of the diphosphine ligand on the metal center, and an electronic one (affecting the overlap between the metal and ligand orbitals),16 which can hardly been disentangled. Though a number of other general descriptors, often based on computational investigations, are also available,17–19 as a matter of fact there are few examples of studies of the donor/acceptor properties of chelating diphosphines (see for instance ref. 20 and 21) or, more in general, chelating ligands (see ref. 22 and 23).

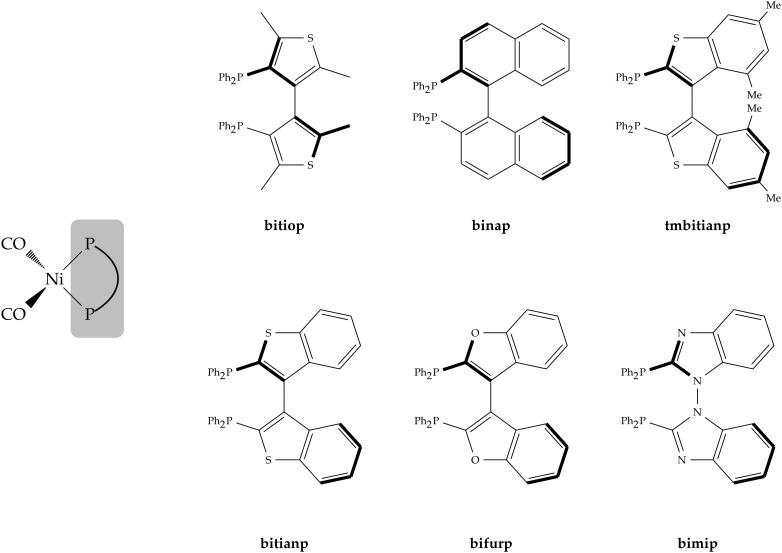
Prompted by the already quoted landmark work of Tolman on monophosphines,2 in this work we decided to synthesize a series of Ni(0) dicarbonyl complexes of general formula [Ni(CO)2(PP)], where PP is a chelating diphosphine, and to address the relation between the carbonyl stretching frequencies and the detailed features of the metal–ligand chemical bond. As for the PP ligands, we focused on a set of six heteroaromatic atropoisomeric ligands, abbreviated hereinafter as bitiop, binap, bitianp, tmbitianp, bifurp and bimip (see a synoptic scheme of their structures in Fig. 1).24–27 Atropoisomeric phosphorus ligands have been established as being extremely efficient in the asymmetric hydrogenation of a wide range of substrates, particularly aryl and heteroaryl ketones.28–30 The series considered in this work has been chosen due to the reliable reaction with [Ni(CO)4] avoiding the formation of mixture or side products. Moreover, atropoisomeric ligands feature a similar bite angle in the nickel dicarbonyl complexes and this minimizes the differences in terms of geometric and steric effects permitting to better focus on the purely electronic ones.

Fig. 1. Chemical structures and abbreviated names for the six chelating diphosphine ligands and nickel dicarbonyl complexes considered in this work.

Fig. 1

Open in a new tab

The article is structured as follows. After providing the experimental methods and computational details (Section 2), we first examine the relation between the observed carbonyl stretching frequencies and some experimental estimates of the electronic properties of the free ligands such as basicity and electrochemical oxidative potentials (Section 3.1). The correlation between these quantities suggests a close relation between the donor ability of the chelating ligand and the carbonyl stretching frequencies observed in the complexes. Then, based on density functional theory (DFT) calculations, we carry out a thorough theoretical analysis (Section 3.2) of the metal–ligand chemical bond by means of a powerful, recently proposed analysis scheme, namely the natural orbitals for chemical valence/charge displacement (NOCV/CD) method.31 Through the NOCV/CD analysis we give a quantitative, spatially detailed description of the several charge fluxes following the metal–ligand bond formation and show that the carbonyl stretching frequencies in the considered complexes selectively respond to the σ-donation charge flow from the phosphorus lone pairs of the ligands, with the frequency shift being in quantitative correlation with the ligand-to-metal transferred charge. We draw conclusions and outline perspectives for future work in the last section (Section 4).

2. Experimental methods and computational details

2.1. Experimental methods

All manipulations involving air-sensitive materials were performed in an inert atmosphere by using standard Schlenk line techniques in nitrogen glassware. All solvents used were anhydrous by fresh distillation under nitrogen before use. Unless otherwise stated, reagents were purchased from commercial sources and used without further purification. Bitiop, tmbitianp, bitianp, bifurp and bimip were synthesized according to procedures reported in the literature.24,27

FTIR spectra of chloroform solutions were collected at room temperature by using a Perkin Elmer (MA, USA) FTIR Spectrometer “Spectrum One” in a spectral region between 2200 and 1600 cm–1 and analyzed using the transmittance technique with 32 scans per ion and 4 cm–1 resolution.

1H, 13C, and 31P NMR spectra were recorded in CDCl3 on a 300 MHz Bruker DRX Avance equipped with a non-reverse probe or a 400 MHz Bruker DRX Avance. Chemical shifts (in ppm) were referenced to a residual solvent proton/carbon peak or using external standard 85% H3PO4 for 31P NMR. Signal multiplicity was determined as s (singlet), d (doublet), t (triplet), q (quartet) or m (multiplet).

General procedure for the synthesis of Ni complexes

The synthesis of the nickel complexes was performed in an NMR tube. To a solution of the diphosphine ligand in CDCl3 (1 mM), one mmol of [Ni(CO)4] was added and the resulting solution was stirred. The reaction was then monitored by 31P NMR. The reaction of [Ni(CO)4] with the diphosphines quickly produced the corresponding tetrahedral dicarbonyl diphosphine complexes. The rigidity of the biaryl backbone allowed the reaction to proceed at room temperature without the production of side products, as stated by the presence of a single peak in the 31P{1H} NMR spectra.

[Ni(CO)2(bitiop)]

1H NMR (300 MHz, CDCl3, 298 K) δ: 8.06 (m, 4H), 7.52 (m, 4H), 7.36 (m, 6H), 7.16 (m, 6H), 1.83 (s, 6H), 1.62 (s, 6H) ppm; 31P{1H} NMR (121.5 MHz, CDCl3, 298 K) δ: 29.5 (s, 2P) ppm; 13C{1H} NMR (75 MHz, CDCl3, 298 K) δ: 201.48 (s), 173.78 (s), 137.57 (s), 136.93–134.88 (m), 132.20 (s), 129.74 (s), 128.81 (s), 128.23 (m), 127.51 (m), 16.38 (s), 14.38 (s) ppm.

[Ni(CO)2(binap)]

1H NMR (300 MHz, CDCl3, 298 K) δ: 8.04 (s, 4H), 7.44 (d, J = 6.4 Hz, 12H), 7.23 (d, J = 7.4 Hz, 6H), 7.02 (s, 2H), 6.86 (d, J = 8.1 Hz, 2H), 6.56 (d, J = 6.0 Hz, 2H), 6.49 (d, J = 6.2 Hz, 4H) ppm; 31P{1H} NMR (121.5 MHz, CDCl3, 298 K) δ: 34.0 (s, 2P) ppm; 13C{1H} NMR (75 MHz, CDCl3, 298 K) δ: 201.48 (s), 173.78 (s), 136.12–135.14 (m), 133.70 (s), 133.25 (s), 132.40 (s), 130.26 (s), 128.93 (s), 128.51 (s), 128.14 (s), 127.91–127.59 (m), 127.59–127.11 (m), 100.30 (s) ppm.

[Ni(CO)2(tmbitianp)]

1H NMR (300 MHz, CDCl3, 298 K) δ: 8.00 (m, 3H), 7.66–7.54 (m, 3H), 7.46 (m, 5H), 7.25 (m, 2H), 7.10 (s, 2H), 6.89–6.72 (m, 5H), 6.56 (s, 2H), 2.29 (s, 6H), 1.67 (s, 6H) ppm; 31P{1H} NMR (121.5 MHz, CDCl3, 298 K) δ: 26.6 (s, 2P) ppm; 13C{1H} NMR (75 MHz, CDCl3, 298 K) δ: 192.00 (s), 141.40 (s), 136.44 (s), 135.70 (s), 134.30 (s), 134.61–133.97 (m), 133.63 (s), 133.19 (d, J = 17.0 Hz), 132.65 (dd, J = 24.2, 10.2 Hz), 131.86 (s), 128.20 (dt, J = 24.1, 11.0 Hz), 21.59 (d, J = 18.9 Hz), 20.19 (s) ppm.

[Ni(CO)2(bitianp)]

1H NMR (300 MHz, CDCl3, 298 K) δ: 7.87 (m, 2H), 7.74 (m, 2H), 7.66 (m, 2H), 7.50 (m, 8H), 7.29 (m, 3H), 7.19 (m, 2H), 7.13 (m, 3H), 6.99 (m, 2H), 6.89 (m, 2H); 31P{1H} NMR (121.5 MHz, CDCl3, 298 K) δ: 22.9 (s, 2P) ppm; 13C{1H} NMR (75 MHz, CDCl3, 298 K) δ: 200.10 (s), 173.84 (s), 140.71 (s), 134.17 (s), 133.95 (s), 132.58 (s), 130.43 (s), 129.23 (s), 128.49 (s), 127.75 (s), 124.64 (s), 124.00 (s), 123.53 (s), 121.87 (s), 99.80 (s) ppm.

[Ni(CO)2(bifurp)]

1H NMR (300 MHz, CDCl3, 298 K) δ: 7.71–7.58 (m, 4H), 7.52 (d, J = 7.6 Hz, 2H), 7.46–7.30 (m, 14H), 7.29–7.14 (m, 8H) ppm; 31P{1H} NMR (121.5 MHz, CDCl3, 298 K) δ: 16.0 (s, 2P) ppm; 13C{1H} NMR (75 MHz, CDCl3, 298 K) δ: 198.43 (s), 192.03 (s), 156.66 (s), 135.48 (d, J = 44.4 Hz), 134.78 (d, J = 37.5 Hz), 134.09–132.46 (m), 129.85 (d, J = 20.6 Hz), 129.13–127.80 (m), 125.71 (s), 123.21 (s), 121.79 (s), 112.22 (s) ppm.

[Ni(CO)2(bimip)]

1H NMR (300 MHz, CDCl3, 298 K) δ: 8.17 (s, 2H), 7.53 (m, 12H), 7.12 (s, 2H), 6.81 (s, 10H), 6.18 (s, 2H) ppm; 31P{1H} NMR (121.5 MHz, CDCl3, 298 K) δ: 18.4 (s, 2P) ppm; 13C{1H} NMR (75 MHz, CDCl3, 298 K) δ: 198.91 (s), 192.02 (s), 133.72 (d, J = 28.1 Hz), 130.51 (d, J = 21.9 Hz), 128.82 (s), 124.23 (s), 123.57 (s), 121.01 (s), 109.42 (s) ppm.

2.2. Computational details

Geometry optimization

Geometry optimization and frequency calculations were performed using density functional theory (DFT) with the Gaussian suite of programs (G09).32 The B3LYP33,34 exchange–correlation functional was adopted, in conjunction with the 6-31+G* basis set35 (see also ref. 36). Semiempirical dispersion contributions were also taken into account by inclusion of Grimme's D3BJ37 model as implemented in Gaussian. Calculations were performed both in vacuo and by including the bulk solvent effects by means of the polarizable continuum model (PCM)38–40 using the integral equation formalism model (IEFPCM) as implemented in Gaussian.41

In the absence of crystallographic data, the structure of the complexes was determined as follows. The ligands were built starting form their X-ray structure.24–27 They were then coordinated to the tetrahedral Ni(CO)2 fragment and the geometry of the resulting complex was optimized. For each complex, several starting points were tested. Five out of six complexes presented a well-defined minimum with a pseudo C 2v geometry at the diphosphine back-bone. For the remaining one, namely the bifurp complex, two minima with comparable energy were found. The lowest-energy one (having pseudo C 2v geometry) is hereafter labeled as bifurp1. The other one (which on the contrary does not show a pseudo C 2v geometry), is labeled as bifurp2. Vibrational analysis confirmed all structures to be true energy minima.

As expected, in all of the considered complexes the ligands showed similar values of the bite angle, with the maximum difference being below 5° (see Table S1 in the ESI†). As mentioned, the bite angle can affect the interaction between the orbitals of the fragments and, in turn, the amount of donation and back-donation between the ligand and the metal. This effect is minimized in our work by the fact that, as just mentioned, all ligands in the considered complexes show a similar bite angle.

Vibrational analysis

As is well known, the inclusion of solvent and anharmonic effects is crucial in order to obtain accurate predictions of vibrational frequencies.

Anharmonic calculations were performed using the GVPT2 model.42,43 Cubic and semi-diagonal quartic force constants were computed by numerical differentiation (with displacements of 0.01 Å) of the analytical Hessian along each active normal coordinate. In order to reproduce anharmonic effects at a reasonable computational cost, a reduced dimensionality (RD) approach was adopted.44,45 In the RD approach, the numerical differentiation is performed only along a subset of modes defined as active, whereas the other modes are treated as harmonic. Reliable results are then obtained if the set of selected active modes is large enough to include all the couplings involved in the frequencies of interest. The carbonyl stretchings are characterized by well-defined and isolated bands, thus it is reasonable to consider only these modes as active in the anharmonic calculations. No significant coupling with other modes has been found.

Using the PCM, the two harmonic carbonyl bands are decreased by about 20 cm–1 with respect to in vacuo calculations. The anharmonic corrections, which as mentioned were obtained at a modest additional computational cost, further red-shifted the bands towards the experimental ones by about 28 cm–1 for all complexes and improved the correlation of the carbonyl stretching frequencies with the ligand-to-metal donation charge transfers (see Fig. S2 in the ESI† and later on in the article). All spectra and coupling matrices were generated and analyzed using the virtual multi-frequency spectrometer Draw (VMS-Draw).46,47

Bond analysis

Bond analysis was performed by means of the recently proposed natural orbitals for chemical valence/charge displacement (NOCV/CD) scheme.31 The NOCV analysis was performed by interfacing G09 with an ad hoc written program‡ (direct implementation of an NOCV module in the Gaussian program suite is presently being pursued). Charge-displacement analysis on discretized electron densities in the form of Gaussian cube files was carried out using the CUBES program suite.48 Integration of the NOCV/CD analysis tools in the CAFFEINE49 molecular visualization software for three-dimensional projection of orbitals and densities in an immersive-virtual-reality (IVR) environment is the subject of current work going on in our group and will be discussed extensively in a forthcoming publication.

3. Results

3.1. Carbonyl stretching frequencies and the electronic properties of the ligands: experimental findings

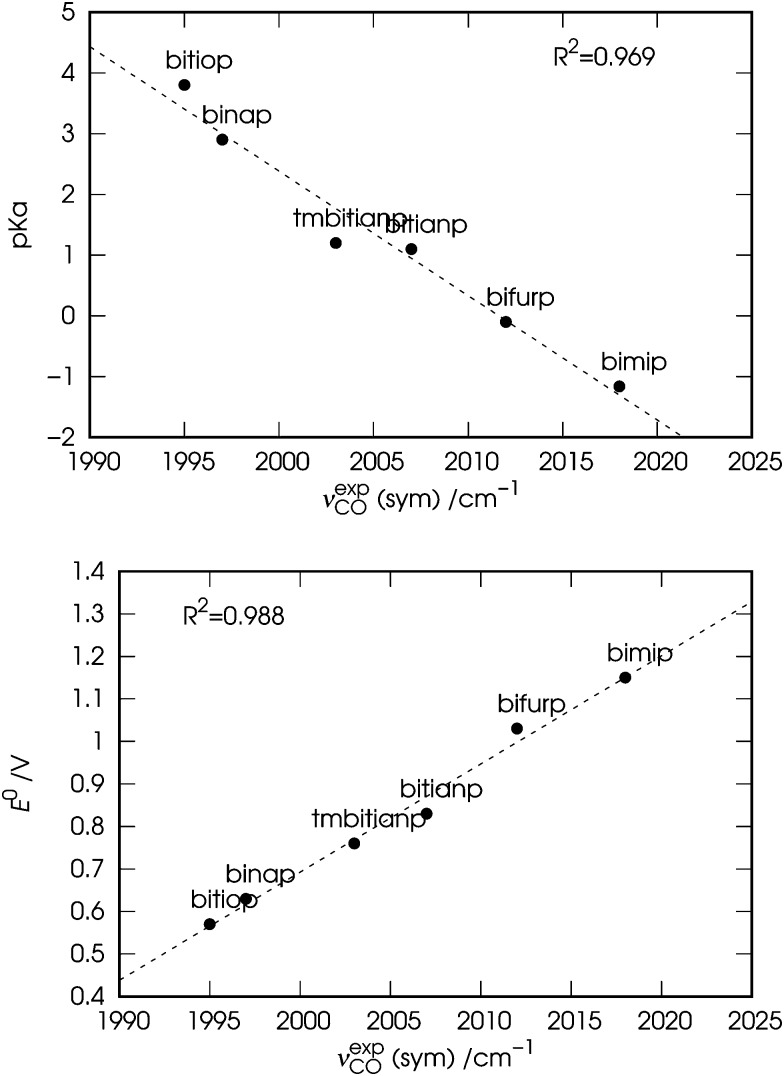
The observed symmetric and antisymmetric carbonyl stretching frequencies (νexpCO) for the six nickel dicarbonyl complexes considered in this work are reported in Table 1. In the same table, experimental estimates of the basicity (pK a) and electrochemical oxidative potential (E 0) of the free ligands are also given.

Table 1. Experimental and calculated properties of the ligands and complexes considered in this work a .

Ligand pK a E 0 (V) ν exp CO (cm–1)
 ν calc CO (cm–1)
Sym. Asym. Sym. Asym.
bitiop 3.8 0.57 1995 1933 2022 1961
binap 2.9 0.63 1997 1936 2025 1965
tmbitianp 1.2 0.76 2003 1944 2028 1970
bitianp 1.1 0.83 2007 1947 2031 1973
bifurp b –0.1 1.03 2012 1953 2036 1979
bimip –1.16 1.15 2018 1961 2043 1986
Open in a new tab

aExperimental basicity (pK a, values from ref. 50) and electrochemical oxidative potential (E 0, values from ref. 27) of the free ligands. Experimental (νexpCO) and calculated (νcalcCO) symmetric and antisymmetric carbonyl stretching frequencies in the nickel complexes.

bCalculated carbonyl stretching frequencies are a weighted average (0.66 : 0.34) of the two conformer contributions (see Section 2).

In a recent work coauthored by some of the present authors, a good correlation between the pK a values of the free ligands and their oxidation potentials E 0 has been noted.50 Both E 0 and pK a have been, in the past, taken as a measure of the σ-donor ability of the ligand (see for instance ref. 27 and 51, respectively), though for the latter objections have been raised for ligands which feature high steric hindrance52 (which however is not the case of the ligands considered herein).

In Fig. 2 the observed values of the symmetric carbonyl stretching frequency (νexpCO) are plotted against the values of pK a (top panel) and E 0 (bottom panel) of the free ligands. Both the plots show a fairly good correlation (R 2 = 0.969 and 0.988, respectively), with slightly better results for the correlation of νexpCO with E 0. The slightly worse correlation between νexpCO and pK a might be due to the fact that the values of pK a might provide a not so accurate description of the basicity of the ligands, since the interaction of their phosphine groups with the hard acid H+ differs significantly from that with the soft ones such as transition metals (Ni in the case of our complexes).53 It is worth noting here that we choose to use the symmetric carbonyl stretching frequencies for consistency with Tolman's approach, although similar results can be obtained using the antisymmetric ones (see Fig. S1 in the ESI†).

Fig. 2. Correlation between the experimental symmetric carbonyl stretching frequencies (νexpCO) of the nickel dicarbonyl complexes with the six considered ligands, and the experimental (i) basicity (pK a, top panel) and (ii) electrochemical oxidative potential (E 0, bottom panel) of the free ligands (see Table 1).

Fig. 2

Open in a new tab

These results, especially in view of the fact that all ligands feature a similar bite angle in the complexes, suggest a close relation between the σ-donor ability of the chelating diphosphines and the carbonyl stretching frequencies in the related nickel dicarbonyl complexes. In particular, the carbonyl stretching frequencies are more red-shifted due to the greater donor power of the chelating ligand. However, the data discussed so far do not allow us to go beyond these considerations and for a deeper understanding a theoretical analysis is in order.

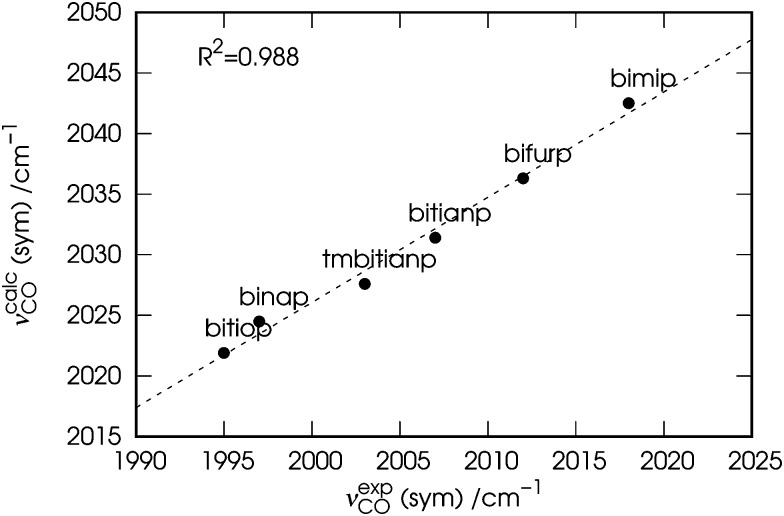
Before moving to the next section, a comment is due. For the sake of consistency, in the following we will use the calculated (νcalcCO) carbonyl stretching frequencies rather than the observed (νexpCO) ones. The values of νcalcCO are given in the rightmost columns of the already discussed Table 1 and are plotted in Fig. 3 against those of νexpCO.

Fig. 3. Correlation between the experimental (νexpCO) and calculated carbonyl stretching frequencies (νcalcCO) of the nickel dicarbonyl complexes with the six considered ligands.

Fig. 3

Open in a new tab

As evident from the figure, despite a blue shift of ∼25 cm–1, a tight correlation (R 2 = 0.988) is found between the two quantities, which makes them indeed interchangeable in any discussion regarding their trend.

3.2. The metal–ligand chemical bond: insights from theory

As mentioned above, in order to investigate the relation between the stretching frequencies of carbonyls and the metal–ligand bonding properties in the set of considered complexes, we made use of the NOCV/CD analysis scheme developed by one of us in collaboration with others.31 While such scheme has been described in detail in ref. 31, we briefly review here its foundations for a clearer reading of the forthcoming discussion.

Within NOCV theory, given an adduct AB formed by fragments A and B, the electron charge rearrangement taking place after the formation of the A–B bond is formulated as the difference Δρ between the total electron density of the adduct and a reference electron density associated with the unbound fragments A and B (where all densities are worked out from single-determinant wavefunctions). This last quantity is constructed from the occupied molecular orbitals of the two isolated fragments (computed using for each fragment the geometry that it has in the adduct), after the same orbitals have been made orthonormal to each other.54–56 Then, by diagonalising the so-called ‘valence operator’ (for which the reader is referred to Nalewajski and Mrozek's valence theory)57–59 and finding its eigenvalues v k and eigenfunctions φ k (termed ‘natural orbitals for chemical valence', NOCVs), Δρ can be decomposed into weighed contributions ascribable to pairs of NOCVs coupled by eigenvalue v k 60

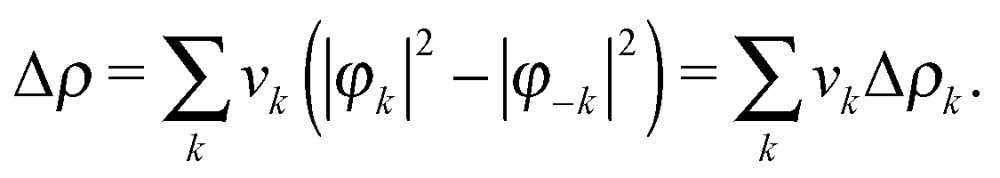3.2. 1

In other words, the total electron charge rearrangement taking place after bond formation results from additive charge flows of v k electrons flowing from orbital φ –k to orbital φ k, with k running over twice the number of occupied molecular orbitals of the adduct. It is worth mentioning here that formalisms have been developed to associate with each of these charge-flow components an energy-contribution term to the overall interaction energy. The reader is referred to the pioneering work of Ziegler56 and Frenking61 for further details on this subject.

Typically, only a few NOCV components in eqn (1) have a significant weight and thus contribute significantly to the overall charge rearrangement, while the remaining components contribute to a negligible extent due to very small-valued weights. Often, a qualitative visual inspection of the few important contributions to the overall charge rearrangement reveals that these have a clear chemical meaning, such as donation and back-donation charge flows, providing a powerful means of understanding the detailed features of the analyzed chemical bond.

To show how this works on a real case, we take the nickel dicarbonyl complex with the ligand bitiop and discuss in detail the results of the related NOCV analysis. In this case, the adduct is the whole [Ni(CO)2(bitiop)] complex at its optimised geometry, and fragments are defined as (i) the Ni(CO)2 moiety and (ii) the bitiop moiety, both frozen at their in-adduct geometries. The largest twelve NOCV eigenvalues v k for this complex are listed in descending order in the second column of Table 2.

Table 2. Weights (NOCV eigenvalues v k) of the first twelve components of the charge rearrangement following metal–ligand bond formation in the nickel dicarbonyl complexes.

bitiop binap tmbitianp bitianp bifurp1 bifurp2 bimip
v 1 0.57 0.57 0.60 0.57 0.58 0.62 0.59
v 2 0.56 0.55 0.55 0.54 0.54 0.53 0.53
v 3 0.32 0.34 0.34 0.34 0.35 0.33 0.35
v 4 0.31 0.31 0.33 0.32 0.33 0.32 0.34
v 5 0.29 0.30 0.31 0.30 0.31 0.31 0.32
v 6 0.27 0.26 0.26 0.26 0.27 0.27 0.27
v 7 0.17 0.16 0.18 0.17 0.17 0.17 0.16
v 8 0.06 0.06 0.07 0.06 0.06 0.06 0.06
v 9 0.06 0.06 0.06 0.06 0.06 0.06 0.06
v 10 0.06 0.05 0.06 0.05 0.05 0.06 0.05
v 11 0.05 0.05 0.05 0.05 0.05 0.05 0.05
v 12 0.05 0.05 0.04 0.05 0.05 0.05 0.04
Open in a new tab

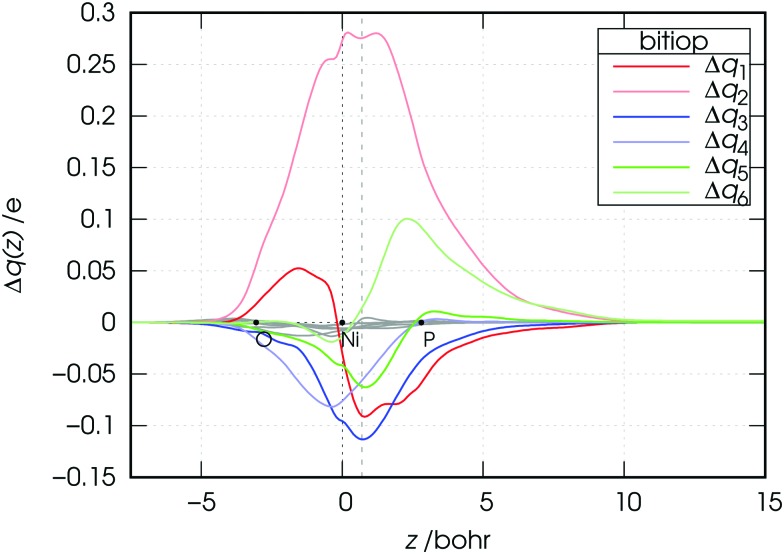
As these data suggest, the overall charge rearrangement following bond formation between the ligand and the metallic moiety results mainly from two components each involving a charge flow of about 0.6 e, and four components each involving a charge flow of about 0.3 e. With the exception of the 7-th component (v 7 = 0.17 e, on which we shall briefly return when commenting on Fig. 5), all remaining NOCV pairs are seen to contribute negligibly to the overall charge rearrangement (v k ≤ 0.06 e).

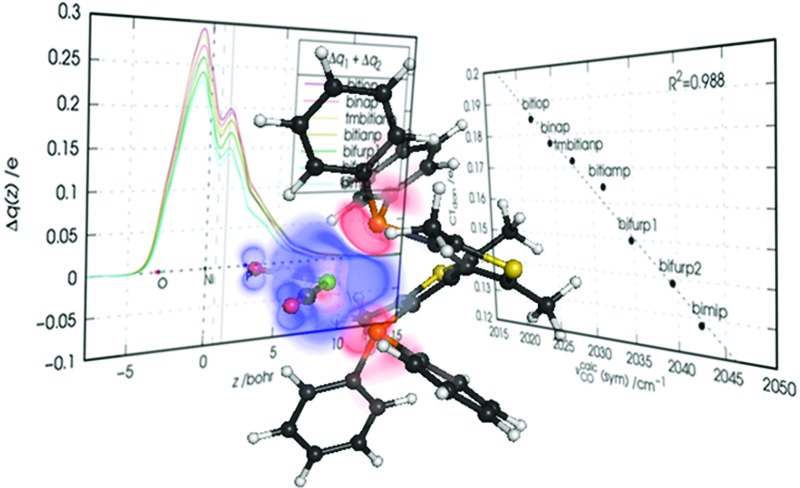
Fig. 5. Charge-displacement curves Δq(z) for the [Ni(CO)2(bitiop)] complex associated with the first six NOCV components of Δρ. Note that the curves associated with NOCV components from 7 to 12 are also displayed as gray lines.

Fig. 5

Open in a new tab

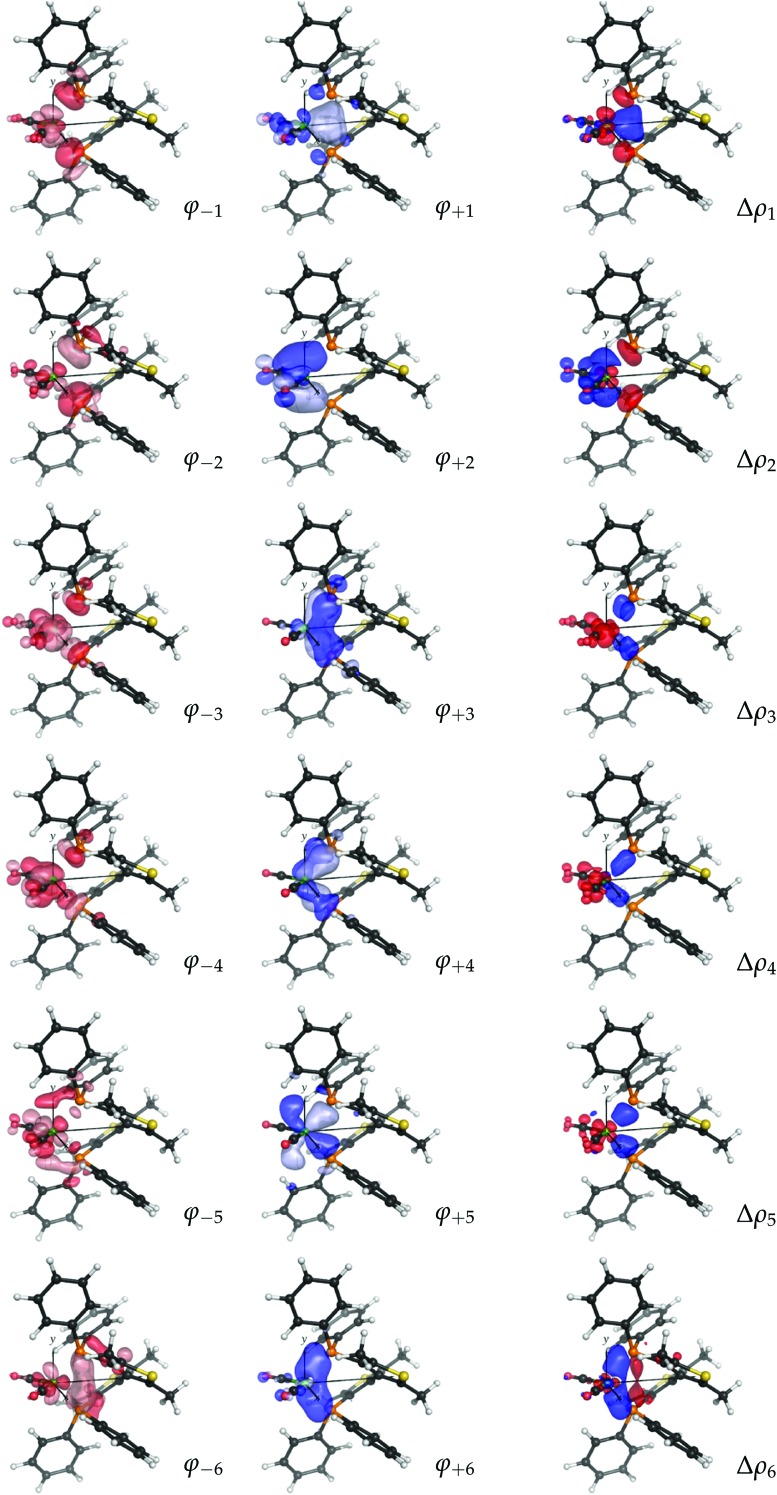
As mentioned, a visual inspection of the NOCV orbital pairs and the associated charge rearrangement can provide chemical insights into the bonding between the analyzed fragments. The first six NOCV orbital pairs (φ –k, φ k) and the associated electron charge rearrangement Δρ k for the bitiop complex are shown in Fig. 4 as isodensity surfaces.

Fig. 4. NOCV pairs (φ –k and φ k, isodensity surfaces at ±0.05 (e Bohr–3)1/2) and associated charge rearrangement (Δρ k, isodensity surfaces at ±0.005 e Bohr–3) taking place after the metal–ligand bond formation in the nickel dicarbonyl complex with the ligand bitiop. In Δρ k plots, red isosurfaces represent regions of electron depletion, blue isosurfaces represent regions of electron accumulation.

Fig. 4

Open in a new tab

Focusing on the first component, following the metal–ligand bond formation a fraction of electrons equal to v 1 = 0.57 e is seen to flow from orbital φ –1 (clearly depicting the phosphorus in-phase lone-pair orbitals and the dy2 orbital of nickel) to orbital φ 1, which displays probability density in the chelation area (see the related charge flow in the Δρ 1 plot, with red lobes indicating electron depletion and blue lobes indicating electron accumulation). Analogously, the second NOCV pair describes the charge flow of 0.56 e from the phosphorus lone pairs and the dyz orbital of nickel (both represented by φ –2) to a molecular orbital φ 2 which displays amplitude on the outer shell of the metal and on the LUMOs of the carbonyls. The associated Δρ 2 plot shows that this component describes a ligand-to-metal donation charge flow. Similarly, a visual inspection of the remaining four components displayed in Fig. 4 (which, as mentioned, contribute to the overall charge rearrangement with half the weight of the first two components), shows that, though less distinctively, components from 3 to 5 can be connected with metal-to-ligand back-donation charge flows while component 6 depicts charge accumulation in-between each Ni–P bond.

The considerations made so far can be summarised as follows. The NOCV analysis conducted on the nickel dicarbonyl complex with bitiop has shown that:

(1) the overall charge rearrangement taking place after the formation of the metal–ligand bond results from a few contributions which can be given a clear chemical meaning;

(2) the first two contributions can be identified as ligand-to-metal donation from the phosphorus lone pairs towards the chelation area and the metallic fragment (with electron charge flowing far into the carbonyl regions and populating the CO anti-bonding LUMOs);

(3) the next four components are associated with charge flows from the metallic fragment to the ligand having π symmetry with respect to each metal–phosphorus bond axis, and with charge accumulation between each Ni–P pair.

Though for the sake of conciseness we do not report here them in full, a visual inspection of the NOCV pairs for the six remaining complexes and an analysis of the data in columns 3–8 of Table 2 show that the three conclusions drawn above for the bitiop complex hold for the other complexes too, with differences that are difficult to interpret through the analysis of the isovalued surfaces. Moreover, caution should be used in taking the values of the eigenvalues v k for a comparison between the complexes. Whereas, in fact, the NOCV eigenvalues provide a measure of the charge flowing between NOCV orbital pairs, this can hardly be taken as an estimation of the charge transfer between fragments as NOCV eigenvalues also include intra-fragment charge rearrangement.31 That's where charge-displacement (CD) analysis comes into play.

The CD scheme is based on the so-called CD function,62 providing a clear and quantitative picture of the charge flow along a selected direction in space, taking place after bond formation.63,64 In particular, the CD function is defined as a progressive partial integration along a suitable axis z of an electron density difference Δρ(x, y, z′)

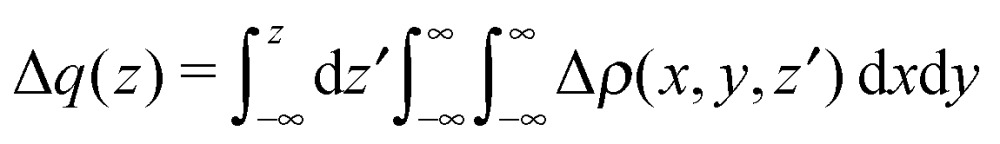3.2. 2

The z axis is usually chosen to be the bond axis between the fragments. Accordingly, the CD function at a given point z quantifies the exact amount of electron charge that, upon formation of the bond, is transferred from right to left (the direction of decreasing z) across a plane perpendicular to the bond axis through z. Negative values of the CD function identify charge flow in the opposite direction. It is worth recalling here that NOCV/CD analysis is here for the first time extended to the case of chelation bonds. Accordingly, to the purpose of assessing the charge transfer between the metallic moiety and the ligand, we choose the z axis as the line bisecting the Inline graphic angle and lying on the Ni(CO)2 plane.

The CD curves related to the first six components of the charge rearrangement following the metal–ligand bond formation in the bitiop complex are displayed in Fig. 5.

The CD curves for components from 7 to 12 are also shown as gray lines. We recall here that the value of the CD function at a given point z represents the exact amount of electron charge that, upon bond formation, has flown from right to left through a plane perpendicular to the z axis through point z. Negative values of the CD function represent charge flow in the opposite direction (from left to right).

The modest entity of the CD curves displayed in gray color confirms that the overall charge rearrangement along the interaction axis upon the metal–ligand bond formation is almost completely recovered by the first six NOCV components, despite the fact that the value of v 7 seemed to be non-negligible compared to the successive v k values. One of these (k = 2, light red) is positive throughout the considered z segment and thus represents charge flow in the metal ← ligand direction throughout the molecular region. For example, the charge transferred from the ligand region to the metallic fragment through the plane orthogonal to the z axis at z = 0.7 Bohr (dashed vertical line) due to component 2 amounts exactly to 0.275 e. Analogously, component 3 (blue curve) depicts charge flux in the metal → ligand direction throughout the molecular region, indicating a charge transfer of –0.113 e (i.e. 0.113 e in the direction from left to right) through the surface identified by the dashed vertical line. For illustrative purposes, the values of all charge transfers (CTs) through this surface are listed in Table 3 for the first twelve NOCV components and all the considered complexes.

Table 3. Charge-transfer values (CTk) across a dividing plane orthogonal to z through z = 0.7 Bohr associated with the first twelve NOCV components of the charge rearrangement taking place after metal–ligand bond formation in the nickel dicarbonyl complexes.

bitiop binap tmbitianp bitianp bifurp1 bifurp2 bimip
CT1 –0.091 –0.021 –0.083 –0.090 –0.097 –0.101 –0.117
CT2 0.275 0.198 0.255 0.254 0.246 0.239 0.245
CT3 –0.113 –0.117 –0.118 –0.120 –0.124 –0.092 –0.127
CT4 –0.056 –0.058 –0.063 –0.060 –0.062 –0.066 –0.065
CT5 –0.062 –0.067 –0.074 –0.069 –0.076 –0.072 –0.075
CT6 0.014 0.007 0.012 0.009 0.006 0.017 0.007
CT7 0.003 0.007 0.008 0.009 0.011 0.007 0.014
CT8 –0.006 –0.004 –0.006 –0.002 –0.005 –0.003 0.001
CT9 –0.005 –0.002 –0.002 –0.005 0.001 –0.000 –0.005
CT10 –0.001 –0.002 –0.001 0.000 –0.000 0.001 0.001
CT11 –0.004 0.000 –0.001 –0.002 –0.001 –0.003 –0.001
CT12 –0.001 –0.001 –0.000 0.001 0.001 –0.000 0.001
Open in a new tab

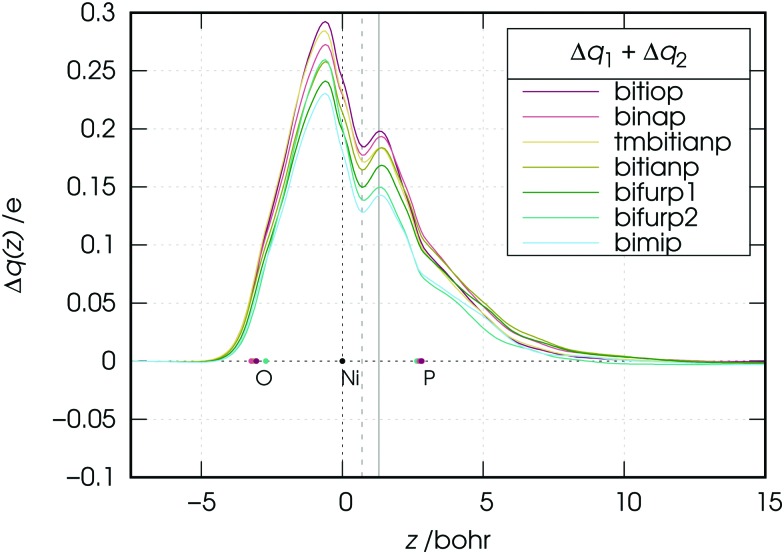
We note now that both components 1 and 2 describe charge flowing from the phosphorus lone-pair orbitals of the ligands (taken either in-phase: component 1, or out-of-phase: component 2) and should be considered together from a chemical point of view. In Fig. 6 the CD curve related to the sum of these two components is reported.

Fig. 6. Charge-displacement curves Δq(z) associated with the sum of the first two NOCV components (charge flowing from the phosphorus lone pairs of the ligands) in the nickel dicarbonyl complexes with the considered ligands. Vertical lines at z = 0.7 and 1.3 Bohr have been used to take quantitative estimates of the ligand-to-metal charge transfers (see text for discussion).

Fig. 6

Open in a new tab

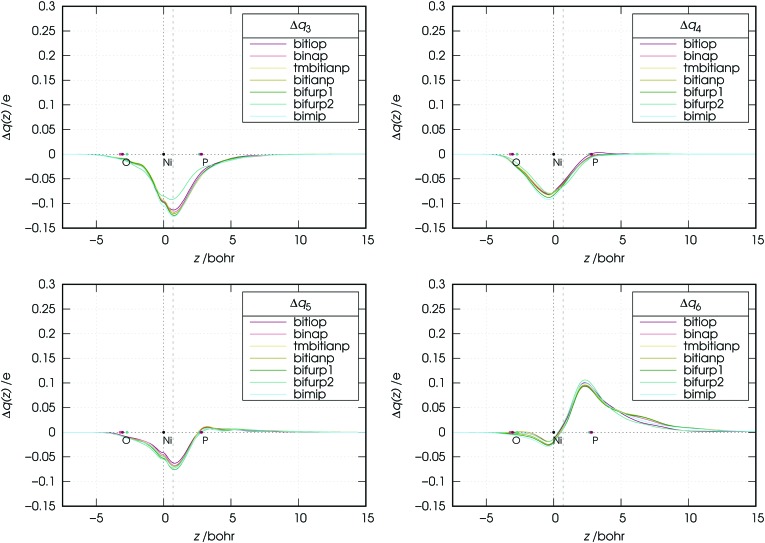
As the figure shows, the overall flux associated with the charge flowing from the lone pairs of the ligands results in a donation flux throughout the whole molecular region and displays a minimum at z = 0.7 Bohr. Moreover, inspection of Fig. 6 shows that there exists a volume region between orthogonal planes to z through z ≃ 0.5 and z ≃ 1.3 Bohr (i.e., in the bond region between Ni and P) where the extent of the charge flowing from right to left (i.e., donated from the phosphorus lone pairs of the ligands to the metal) as a function of the ligand reflects the order of the carbonyl stretching frequencies in the related complexes. This feature, as clearly shown by Fig. 7, is never observed in the curves related to components 3–6, which moreover display no big variation on going from complex to complex (neither their combination, though not shown here, does).

Fig. 7. Charge-displacement curves (Δq(z)) associated with the k-th (k = 3, 4, 5, 6) NOCV component in the nickel dicarbonyl complexes with the considered ligands.

Fig. 7

Open in a new tab

An exception seems to appear in the plot of the NOCV component 3. In this plot, the curve of the bifurp2 complex is, in fact, markedly higher than those of the other complexes. This is certainly due to the fact that, as mentioned in Section 2, bifurp2 has a different geometry from all other complexes, which evidently decreases the amount of metal-to-ligand back-donation.

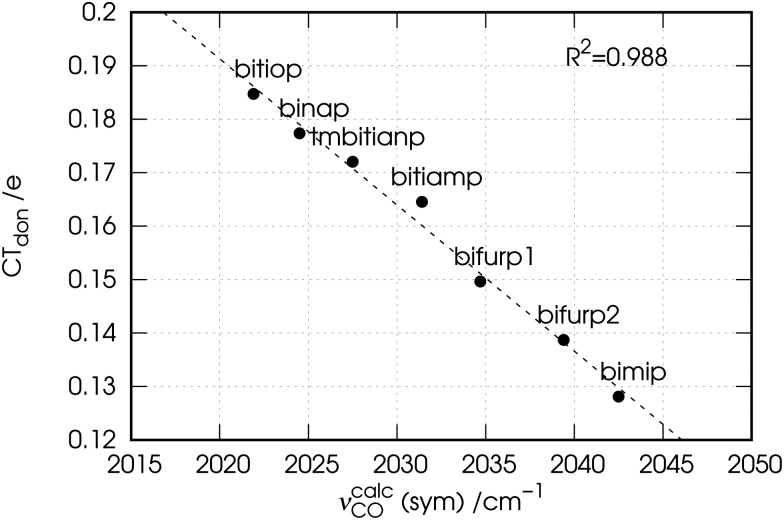
Now, as mentioned above, the CD curves depicting the charge flow associated with charge depletion from the lone pairs of the ligands (i.e., the sum of components 1 and 2), reflect over a relatively wide segment of z localized in the metal–ligand bond region the same order that the observed carbonyl stretching frequencies have in the series of the considered complexes. This confirms the hypothesis made in Section 3.1 on the basis of experimental data that there is a correlation between donation from the lone pairs and the red-shift response of the carbonyl stretching frequencies in the complexes. To put this on a quantitative ground we plot in Fig. 8 the associated charge transfer CTdon = CT1 + CT2 taken at z = 0.7 Bohr, against the carbonyl stretching frequencies for the considered complexes.

Fig. 8. Correlation between the calculated carbonyl stretching frequencies (νcalcCO) and the charge transfer (CTdon = CT1 + CT2) associated with the ligand-to-metal donation from the phosphorus lone pairs.

Fig. 8

Open in a new tab

The figure shows that indeed there is a tight correlation between the two quantities with R 2 = 0.988. The correlation remains high also at the boundaries of the mentioned z segment, yielding R 2 = 0.986 if CTs are taken at z = 0.5 Bohr and R 2 = 0.965 if CTs are taken at z = 1.3 Bohr. The fact that bifurp2, with its peculiar geometry and lower amount of metal-to-ligand back-donation, perfectly fits this trend cannot but confirm that in the set of the considered complexes it is solely the ligand-to-metal σ-donation that the carbonyl stretching frequencies respond to.

4. Conclusions

In this paper we addressed the issue of the relation between spectroscopic observables and the detailed metal–ligand bonding features in coordination complexes from the original perspective of chelation bonds.

A set of six nickel dicarbonyl complexes with chelating diphosphine ligands were synthesized and experimentally characterized, and a preliminary analysis of the experimental data showed that the observed carbonyl stretching frequencies in the complexes are in good correlation with the electronic properties of the ligands, such as basicity (R 2 = 0.969) and electrochemical oxidative potentials (R 2 = 0.988), which can be taken as an estimate of their σ-donor power. This prompted us to perform a thorough theoretical investigation for a deeper understanding of the features of the metal–ligand chemical bond in the considered complexes. To this purpose the recently proposed natural orbitals for the chemical valence/charge displacement (NOCV/CD) approach was adopted and here for the first time extended to the analysis of chelation bonds. The NOCV/CD analysis of the charge rearrangement taking place upon the metal–ligand bond formation computed by means of density functional theory (DFT), allowed us to single out on a quantitative basis the main components of the metal–ligand interaction in terms of charge flows between the molecular orbitals of the fragments.

We first analyzed in-depth the metal–ligand bonding features for one of the considered complexes, namely that with bitiop. The results showed that the metal–ligand bond formation involves mainly charge flows from the phosphorus lone pairs of the ligands towards both the chelation area and the metallic fragment, with partial charge flowing far into the carbonyl region. The remaining charge-rearrangement components involve mainly metal-to-ligand back-donation and charge accumulation between each Ni–P pair. The analysis of the remaining complexes showed that this picture holds for all complexes considered in this work. Then we carried out a cross-comparison on quantitative grounds of the results obtained for the other complexes and showed that it is the bond component associated with charge flowing from the lone pairs of the ligands that quantitatively drives the response of the carbonyl stretching frequencies to the metal–ligand bond formation, with these latter tightly correlating (R 2 = 0.988) with the metal-to-ligand charge-transfer estimates.

The present results, achieved by both experiment and state-of-the-art theoretical/computational methods, on one hand indicate a method of quantitatively assessing the donor power of chelating ligands in homogeneous catalysis from simple experimental measurements–thus providing a useful tool for designing and predicting the efficiency of new catalysts. On the other hand, they shed light on the nature of chelation bonds themselves confirming the robustness of the NOCV/CD analysis scheme and opening the way to promising future investigations in the field of coordination chemistry, such as accounting for ligands featuring different bite angles in order to quantitatively assess the bite-angle effect on the electronic properties at the metal center.

Acknowledgments

The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. [320951].

Footnotes

†Electronic supplementary information (ESI) available: Antisymmetric νexpCOvs. pK a and E 0, calculated β angles, correlation between CTdon and νcalcCO, experimental 1H, 13C{1H}, 31P{1H} NMR spectra of complexes, and optimized geometries of the complexes. See DOI: 10.1039/c7cp00982h
Click here for additional data file. (1.8MB, pdf)

‡S. Rampino, The WAVERLEY program package, see http://www.srampino.com/code.html#Waverley (accessed 4 January 2017).

References

  1. Kamer P. C. and van Leeuwen P. W., Phosphorus(iii) ligands in homogeneous catalysis: design and synthesis, John Wiley & Sons, 2012. [Google Scholar]
  2. Tolman C. A. J. Am. Chem. Soc. 1970;92:2953–2956. [Google Scholar]
  3. Tolman C. A. Chem. Rev. 1977;77:313–348. [Google Scholar]
  4. Herzberg G., Molecular spectra and molecular structure, Read Books Ltd, 1950, vol. 1. [Google Scholar]
  5. Bellamy L. J., Carbonyl Frequencies, Springer Netherlands, Dordrecht, 1980, pp. 128–194. [Google Scholar]
  6. Valyaev D. A., Brousses R., Lugan N., Fernández I., Sierra M. A. Chem. – Eur. J. 2011;17:6602–6605. doi: 10.1002/chem.201100651. [DOI] [PubMed] [Google Scholar]
  7. Setiawan D., Kalescky R., Kraka E., Cremer D. Inorg. Chem. 2016;55:2332–2344. doi: 10.1021/acs.inorgchem.5b02711. [DOI] [PubMed] [Google Scholar]
  8. Alcarazo M. Acc. Chem. Res. 2016;49:1797–1805. doi: 10.1021/acs.accounts.6b00262. [DOI] [PubMed] [Google Scholar]
  9. Ehlers A. W., Dapprich S., Vyboishchikov S. F., Frenking G. Organometallics. 1996;15:105–117. [Google Scholar]
  10. Massera C., Frenking G. Organometallics. 2003;22:2758–2765. [Google Scholar]
  11. Leyssens T., Peeters D., Orpen A. G., Harvey J. N. Organometallics. 2007;26:2637–2645. [Google Scholar]
  12. Tonner R., Frenking G. Organometallics. 2009;28:3901–3905. [Google Scholar]
  13. Tognetti V., Joubert L., Cortona P., Adamo C. J. Phys. Chem. A. 2009;113:12322–12327. doi: 10.1021/jp9045534. [DOI] [PubMed] [Google Scholar]
  14. Dierkes P., van Leeuwen P. W. N. M. J. Chem. Soc., Dalton Trans. 1999:1519–1530. [Google Scholar]
  15. Freixa Z., van Leeuwen P. W. N. M. Dalton Trans. 2003:1890–1901. [Google Scholar]
  16. Fey N. Dalton Trans. 2010;39:296–310. doi: 10.1039/b913356a. [DOI] [PubMed] [Google Scholar]
  17. Fey N., Harvey J. N., Lloyd-Jones G. C., Murray P., Orpen A. G., Osborne R., Purdie M. Organometallics. 2008;27:1372–1383. doi: 10.1021/om300312t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Jover J., Fey N., Harvey J. N., Lloyd-Jones G. C., Orpen A. G., Owen-Smith G. J. J., Murray P., Hose D. R. J., Osborne R., Purdie M. Organometallics. 2012;31:5302–5306. doi: 10.1021/om300312t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jover J., Fey N. Dalton Trans. 2013;42:172–181. doi: 10.1039/c2dt32099a. [DOI] [PubMed] [Google Scholar]
  20. Flener Lovitt C., Frenking G., Girolami G. S. Organometallics. 2012;31:4122–4132. [Google Scholar]
  21. Donahue C. M., McCollom S. P., Forrest C. M., Blake A. V., Bellott B. J., Keith J. M., Daly S. R. Inorg. Chem. 2015;54:5646–5659. doi: 10.1021/ic503125b. [DOI] [PubMed] [Google Scholar]
  22. Ardizzoia G. A., Bea M., Brenna S., Therrien B. Eur. J. Inorg. Chem. 2016:3829–3837. [Google Scholar]
  23. Canac Y., Lepetit C. Inorg. Chem. 2017;56:667–675. doi: 10.1021/acs.inorgchem.6b02610. [DOI] [PubMed] [Google Scholar]
  24. Benincori T., Brenna E., Sannicolò F., Trimarco L., Antognazza P., Cesarotti E., Demartin F., Pilati T. J. Org. Chem. 1996;61:6244–6251. doi: 10.1021/jo960211f. [DOI] [PubMed] [Google Scholar]
  25. Benincori T., Cesarotti E., Piccolo O., Sannicolò F. J. Org. Chem. 2000;65:2043–2047. doi: 10.1021/jo991533x. [DOI] [PubMed] [Google Scholar]
  26. Benincori T., Brenna E., Sannicolò F., Trimarco L., Antognazza P., Cesarotti E., Demartin F., Pilati T., Zotti G. J. Organomet. Chem. 1997;529:445–453. [Google Scholar]
  27. Benincori T., Piccolo O., Rizzo S., Sannicolò F. J. Org. Chem. 2000;65:8340–8347. doi: 10.1021/jo001207d. [DOI] [PubMed] [Google Scholar]
  28. Doucet H., Ohkuma T., Murata K., Yokozawa T., Kozawa M., Katayama E., England A. F., Ikariya T., Noyori R. Angew. Chem. 1998;110:1792–1796. doi: 10.1002/(SICI)1521-3773(19980703)37:12<1703::AID-ANIE1703>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
  29. Qiu L., Kwong F. Y., Wu J., Lam W. H., Chan S., Yu W.-Y., Li Y.-M., Guo R., Zhou Z., Chan A. S. C. J. Am. Chem. Soc. 2006;128:5955–5965. doi: 10.1021/ja0602694. [DOI] [PubMed] [Google Scholar]
  30. Rimoldi I., Cesarotti E., Zerla D., Molinari F., Albanese D., Castellano C., Gandolfi R. Tetrahedron: Asymmetry. 2011;22:597–602. [Google Scholar]
  31. Bistoni G., Rampino S., Tarantelli F., Belpassi L. J. Chem. Phys. 2015;142:084112. doi: 10.1063/1.4908537. [DOI] [PubMed] [Google Scholar]
  32. Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery Jr J. A., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J. and Fox D. J., Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009.
  33. Lee C., Yang W., Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
  34. Becke A. D. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
  35. Rassolov V. A., Ratner M. A., Pople J. A., Redfern P. C., Curtiss L. A. J. Comput. Chem. 2001;22:976–984. [Google Scholar]
  36. Kvapilová H., Vlček A., Barone V., Biczysko M., Záliš S. J. Phys. Chem. A. 2015;119:10137–10146. doi: 10.1021/acs.jpca.5b07585. [DOI] [PubMed] [Google Scholar]
  37. Grimme S., Ehrlich S., Goerigk L. J. Comput. Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  38. Barone V., Cossi M., Tomasi J. J. Chem. Phys. 1997;107:3210–3221. [Google Scholar]
  39. Cossi M., Scalmani G., Rega N., Barone V. J. Chem. Phys. 2002;117:43–54. [Google Scholar]
  40. Tomasi J., Mennucci B., Cammi R. Chem. Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  41. Scalmani G., Frisch M. J. J. Chem. Phys. 2010;132:114110. doi: 10.1063/1.3359469. [DOI] [PubMed] [Google Scholar]
  42. Barone V. J. Chem. Phys. 2005;122:014108. doi: 10.1063/1.1824881. [DOI] [PubMed] [Google Scholar]
  43. Bloino J., Barone V. J. Chem. Phys. 2012;136:124108. doi: 10.1063/1.3695210. [DOI] [PubMed] [Google Scholar]
  44. Barone V., Biczysko M., Bloino J., Borkowska-Panek M., Carnimeo I., Panek P. Int. J. Quantum Chem. 2012;112:2185–2200. [Google Scholar]
  45. Barone V., Biczysko M., Bloino J. Phys. Chem. Chem. Phys. 2014;16:1759–1787. doi: 10.1039/c3cp53413h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Barone V. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2016;6:86–110. doi: 10.1002/wcms.1238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Licari D., Baiardi A., Biczysko M., Egidi F., Latouche C., Barone V. J. Comput. Chem. 2015;36:321–334. doi: 10.1002/jcc.23785. [DOI] [PubMed] [Google Scholar]
  48. Rampino S. VIRT&L-COMM. 2015;7:6. [Google Scholar]
  49. Salvadori A., Del Frate G., Pagliai M., Mancini G., Barone V. Int. J. Quantum Chem. 2016;116:1731–1746. doi: 10.1002/qua.25207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Facchetti G., Cesarotti E., Pellizzoni M., Zerla D., Rimoldi I. Eur. J. Inorg. Chem. 2012:4365–4370. [Google Scholar]
  51. Golovin M. N., Rahman M. M., Belmonte J. E., Giering W. P. Organometallics. 1985;4:1981–1991. [Google Scholar]
  52. Kühl O. Coord. Chem. Rev. 2005;249:693–704. [Google Scholar]
  53. Pacchioni G., Bagus P. S. Inorg. Chem. 1992;31:4391–4398. [Google Scholar]
  54. Mitoraj M., Michalak A. J. Mol. Model. 2007;13:347–355. doi: 10.1007/s00894-006-0149-4. [DOI] [PubMed] [Google Scholar]
  55. Michalak A., Mitoraj M., Ziegler T. J. Phys. Chem. A. 2008;112:1933–1939. doi: 10.1021/jp075460u. [DOI] [PubMed] [Google Scholar]
  56. Mitoraj M. P., Michalak A., Ziegler T. J. Chem. Theory Comput. 2009;5:962–975. doi: 10.1021/ct800503d. [DOI] [PubMed] [Google Scholar]
  57. Nalewajski R. F., Köster A. M., Jug K. Theor. Chim. Acta. 1993;85:463–484. [Google Scholar]
  58. Nalewajski R. F., Mrozek J. Int. J. Quantum Chem. 1994;51:187–200. [Google Scholar]
  59. Nalewajski R. F., Mrozek J., Michalak A. Int. J. Quantum Chem. 1997;61:589–601. [Google Scholar]
  60. Radoń M. Theor. Chem. Acc. 2008;120:337–339. [Google Scholar]
  61. Frenking G. and Matthias Bickelhaupt F., The EDA Perspective of Chemical Bonding, Wiley-VCH Verlag GmbH & Co. KGaA, 2014, pp. 121–157. [Google Scholar]
  62. Belpassi L., Infante I., Tarantelli F., Visscher L. J. Am. Chem. Soc. 2008;130:1048–1060. doi: 10.1021/ja0772647. [DOI] [PubMed] [Google Scholar]
  63. Rampino S., Storchi L., Belpassi L. J. Chem. Phys. 2015;143:024307. doi: 10.1063/1.4926533. [DOI] [PubMed] [Google Scholar]
  64. Bistoni G., Rampino S., Scafuri N., Ciancaleoni G., Zuccaccia D., Belpassi L., Tarantelli F. Chem. Sci. 2016;7:1174–1184. doi: 10.1039/c5sc02971f. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (1.8MB, pdf)

Articles from Physical Chemistry Chemical Physics are provided here courtesy of Royal Society of Chemistry

RESOURCES