The Dynamics of Hospital Use among Older People Evidence for Europe Using SHARE Data

Abstract

Objective

Hospital services use, which is a major driver of total health expenditures, is expected to rise over the next decades in Europe, especially because of population aging. The purpose of this article is to better understand the dynamics of older people's demand for hospital care over time in a cross‐country setting.

Data source

We used data from the Survey on Health, Ageing, and Retirement in Europe (SHARE), in 10 countries between 2004 and 2011.

Study Design

We estimated a dynamic panel model of hospital admission for respondents aged 50 years or more.

Principal Findings

Following prior research, we found evidence of state dependence in hospital use over time. We also found that rise in frailty—among other health covariates—is a strong predictor of increased hospital use. Progression by one point on the frailty scale [0;5] is associated with an additional risk of about 2.1 percent on average.

Conclusions

Our results support promotion of early detection of frailty in primary care, and improvement of coordination between actors within the health system, as potential strategies to reduce avoidable or unnecessary hospital use among frail elderly.

Hospital services use, which is a major driver of total health expenditures, is expected to rise over the next decades in Europe, especially because of population aging (Kohn and Liu 2013; Ilinca and Calciolari 2015). Hospitals services, which are traditionally the major source of long‐term care expenditure (Forder 2009), have been at the core of many recent measures aimed at cutting costs and gaining efficiency. A central aspect is in the management of disease by primary care producers, which can lead to large savings due to prevented hospitalizations (Dusheiko et al. 2011). In that context, most European countries are refocusing health policy on health promotion and disability prevention among older people. From an economic perspective, reducing nonplanned hospitalization can lead to large savings. Previous research provided evidence that almost 5 percent of the hospitals' production costs were dedicated to the holding of reserve capacity to service this stochastic demand (Hughes and McGuire 2003). The purpose of this article is to better understand the drivers of older people's demand for hospital care over time in a cross‐country setting.

Modeling individuals' demand for hospital care in the elderly population is a complex process. Three key aspects must be taken into consideration. First, hospitalization should be modeled as a dynamic process. In Britain, previous research provided evidence that past hospitalization was associated with lower future length of stays in individuals' hospital use (Kohn and Liu 2013). That hospitalization use should be modeled as a dynamic process was confirmed in Norway, were hospital readmission was lower for patients experiencing longer length of stays (Bjorvatn 2013). Second, models should control for patterns of primary care providers' visits, as they play a central role in such hospital use dynamics. The quality of the care produced by general practitioners (GPs) in Norway was a key predictor of hospital use (Carlsen et al. 2007). Financial incentive schemes provided to GPs in Italy were associated with lower rates of preventable hospital admissions (Fiorentini et al. 2011). Third, health covariates should include measures of frailty to get a more accurate assessment of older people's need for care. Frailty is found to be a strong predictor of higher older people's hospital use over time (McAdams‐DeMarco et al. 2013; Ilinca and Calciolari 2015).

Our original contribution is to combine these three key aspects to develop a comprehensive model of older people's hospitalization use over time. In the detail, we estimated a dynamic panel model of hospital admission for more than 7,500 respondents of the Survey on Health, Ageing, and Retirement in Europe (SHARE) in 10 countries between 2004 and 2011. Using the reference methodology defined by Kohn and Liu (2013), we specified a dynamic model for hospital use.

Special attention is given to the assumption of state‐dependency of medical health care to explain the dynamics of hospital admissions. We explore the role of visits to GPs in the explanation of the hospital use dynamic. We also explore to what extent hospital care is a substitute to specialist practitioners (SPs) service. We control for health by using a set of covariates, including a new measure of frailty (Fried et al. 2001, 2004; Lang, Michel, and Zekry 2009) since frailty is a transitional state from healthy aging to functional decline.

Data

Source and Sample

SHARE is a multidisciplinary and cross‐national cohort of individual data on health, socio‐economic status and social and family relationships of more than 80,000 respondents aged 50 years or older (Borsch‐Supan et al. 2013). Eleven countries contributed to the 2004 SHARE baseline study (Israel took also part in SHARE wave 1 only). They are a balanced representation of the various regions in Europe, ranging from Scandinavia (Denmark and Sweden) through Central Europe (Austria, France, Germany, Switzerland, Belgium, and the Netherlands) to the Mediterranean (Spain, Italy, and Greece). Further data were collected in 2006–2007 during the second wave of SHARE in these countries, the Czech Republic, Poland, and Ireland. SHARELIFE, the third wave of the project, was conducted in 2008–2009 over the same population (apart from Ireland). This time, the respondents were interviewed about their life history. Different fields such as childhood health, education, job career, family life, housing, and so on were surveyed and provide useful information on initial conditions and life course. In 2010, Greece dropped from the survey (as a consequence of the economic crisis) while Estonia, Slovenia, Hungary, and Portugal joined SHARE wave 4, which is the third regular panel wave of the survey following the SHARELIFE life history questionnaire.

The sample retained here is balanced; it is made of the three regular panel waves and a retrospective one. It is restricted to the 10 baseline countries, which did carry all of the four waves in northern (Denmark, Sweden, the Netherlands), continental (Austria, Germany, France, Belgium, Switzerland), and southern (Italy, Spain) regions of Europe. Finally, only full‐rank data matrices are kept at each wave so that respondents with missing data are deleted. Our final sample consisted of 30,248 observations made of 7,562 individuals repeatedly surveyed each time during the first four waves of SHARE.

Description of the Variables

Our dependent variable is a dichotomous variable measuring whether, during the last 12 months, the respondent has been in a hospital overnight. Our explanatory variables of interest measured whether the respondent has seen or talked to a GP about his/her health and has consulted any of the SP mentioned on a list. We also created three lag variables measuring the use of GPs, SPs or hospital during the previous wave. Following prior work (Santos‐Eggimann et al. 2009), we derived Fried's frailty measure based on five criteria (exhaustion, shrinking, weakness, slowness, and low activity) corresponding to various subjective and objective health measures in SHARE. The initial score of frailty takes its values in the interval [0;5] since one point was allocated for each fulfilled criterion.

In addition to these variables of interest, we controlled for several indicators of health status to take into account the need for care. A dichotomous variable was created for each of the following health measure: self‐rated health (SRH) being fair or poor; multimorbidity for at least two chronic diseases; two or more functional limitations Katz's activities of daily living (ADLs) and Lawton's instrumental activities of daily living (IADLs); and the Euro‐D measure for depressive symptoms (Prince et al. 1999). A composite health index was derived from a multiple correspondence analysis of the previous health measures and a dichotomous variable is created for general “poor health.” The multiple correspondence analysis (Greenacre 2006) results indicate that the first component captures most of the information in the binary health variables. Individual coordinates of the first axis thus provide a synthetic health index made of a nonlinear combination of the binary health variables. Since positive values and negative values of this index reflect general poor or good health, a binary index was derived for the sake of simplicity. The health index is made of the individuals' coordinates on the first axis as a data reduction approach. We substituted this health index for all health variables but frailty in another model to test for change in standard errors due to potential multicolinearity as there is a wide array of health measures in the covariates. As the results were identical, we are confident in our estimates with full health measure, which gives the reader a better appraisal on the economic importance of each health condition on hospital stay. This measure provided a good summary of trends in health over the period. Additional covariates include a measure of income adequacy on a 4‐point scale, whether the household is able to make ends meet: 1‐with great difficulty, 2‐with some difficulty, 3‐fairly easily, or 4‐easily. Income adequacy is the only measure of economic well‐being that is consistent over the different waves of SHARE—as measures of income and assets changed between waves 1 and 2. Finally, we control for a variable measuring the presence of health problems in adult life. This variable is taken from SHARELIFE, the retrospective survey that took place in wave 3. Respondents were asked about their life history. “Health problems in adult life” is a binary index of health, taking the value 1 if the respondent reports any periods of ill health over the life‐cycle (>1 year) or if she reports any physical injury over the lifecycle (>1 year). As health problems and hospital use in late life is found to be associated with health factors in early‐ and mid‐life (Freedman et al. 2008), this variable is used as a proxy for hospital use before the start of the prospective panel.

Methods

We used dynamic panel models for binary outcome. The simple estimation procedure suggested by Wooldridge contributed to render these methods increasingly popular in applied economics (Wooldridge 2005). We followed a seminal application to health economics that was provided in previous research (Contoyannis, Jones, and Rice 2004) and recently applied to hospital care consumption (Kohn and Liu 2013). Following that model, we used a dynamic specification by including an autoregressive one‐period lag of the hospital use variable to reflect persistence, or state dependence.

Let y _it denote the binary outcome of hospital stays for individual i, i = 1, … , N, at time t, t = 1, …,T. Let X _it denote the full‐rank data matrix of explanatory variables. We assumed additive unobserved heterogeneity in a dynamic probit model such as:

$$P(y_{it}=1|y_{it-1},X_{it},c_i)=\mathrm{\Phi }(\mathit{\rho }{y}_{it-1}+X_{it}\mathit{\beta }+c_i)$$ (1)

where c _i is the unobserved individual specific term and Φ is the normal cumulative distribution function. Unlike in the static case, dynamic panel models typically rest on sequential moments restrictions (Chamberlain 1992). However, the usual random effect assumption of strict independence between c _i and X _it is too strong in the case of individual micro‐data. We therefore allowed some correlation between the unobservable and the explanatory variables in order to retain a more realistic assumption. Following previous research (Ilinca and Calciolari 2015), we applied a Mundlak‐Chamberlain device where the individual fixed effect is netted out using a constant and a time‐trend:

$$c_i=\mathit{\psi }+{\overline{X}}_i\mathit{\xi }+{\mathit{\xi }}_0{y}_{i0}+a_i$$ (2)

where c _i, the unobserved individual effect is replaced by its linear projection onto ${\overline{X}}_i$, the means of the regressors, and where ψ is the intercept, y _i0 is the initial value of y _it prior to the start of the survey, and a _i represents the projection error. Our assumption is an application of the Mundlak‐Chamberlain device where the individual fixed effect is netted out using a constant and a time‐trend. An advantage of this methodology is that our model estimates are not subject to omitted variable bias as long as the omitted variables are time‐invariant. In other words, controlling for gender, age, education, being a migrant, or other individual fixed effects would not modify the parameters of the time‐varying variables. Similarly, average partial effects for the explanatory variables can now be interpreted as within estimates, just like an alleged “fixed effects probit” model would yield.

The use of y _i0 prevents inconsistent estimates—known as the problem of initial conditions (Heckman 1981). Although it is general practice to use the first wave observation as the initial value of the dependent variable, life‐history data from wave 3 (SHARELIFE) allow us to use retrospective information as a good proxy for y _i0. Doing so, we kept the first regular panel wave for the analysis so that T = 3 is sufficient for a dynamic estimation. Indeed, panel data analysis requires at least two periods to analyze at least one transition, if the panel model includes a lagged variable, then another time period is needed. We opted for the variable health problems in adult life, a binary retrospective index of health taking the value 1 if the respondent reported any periods of ill health over the life‐cycle (>1 year) or if she reported any physical injury over the lifecycle (>1 year).

Lee (2005) points out that dynamic panel models usually rely on the implicit assumption that one lag of the dependent variable is sufficient to fully capture the dynamics of the process (Lee 2005). Past hospital use may be associated with other health care use in the preceding period, especially specialist care since in some European countries, specialist care can only be found at the hospital. Put differently, it may also be that visit to GPs and SPs at t − 1 would be associated with hospital visit at t − 1, either as complement or substitute care to hospital visit (Carlsen et al. 2007; Ilinca and Calciolari 2015). As a consequence, visit to GPs and SPs at t − 1 are included as control variables besides hospital visits at t − 1. In addition, visit to GPs and SPs at t are also included as determinants of hospital visits at time t. Other covariates include health measures, the variable of make‐ends‐meet, time dummies (to correct for the time‐spell between regular panel waves 1, 2, and 4), and a constant.

We used simple structural coefficient tests to define our model specification. These tests supported the dynamic approach, failed to reject the Mundlak‐Chamberlain device, and failed to reject the influence of initial conditions, meaning that a genuinely new process is observed at the beginning of the sample. We can easily extend the specification of (1) to achieve dynamic completeness; under assumption (2), this defines a latent variable regression model:

$$y_{it}^{\ast }=Z_{it-1}\mathit{\delta }+X_{it}\mathit{\beta }+{\overline{X}}_i\mathit{\xi }+{\mathit{\xi }}_0{y}_{i0}+a_i+{\mathit{\epsilon }}_{it}$$ (3.1)

$$\text{with}{Z}_{it-1}\mathit{\delta }={\mathit{\delta }}_y{y}_{it-1}+{\mathit{\delta }}_{gp}G{P}_{it-1}+{\mathit{\delta }}_{SP}S{P}_{it-1}$$ (3.2)

$$\text{and}{X}_{it}\mathit{\beta }={\mathit{\beta }}_{gp}G{P}_{it}+{\mathit{\beta }}_{sp}S{P}_{it}+Z_{it}{\mathit{\beta }}_z$$ (3.3)

where Z _it contains health measures, the variable of make‐ends‐meet, time dummies (to correct for the time‐spell between regular panel waves 1, 2, and 4), and the constant ψ. We also assume that $a_i|X_{it}\sim N(\mathit{\psi }+{\overline{X}}_i\mathit{\xi },{\mathit{\sigma }}_a^2)$ and ɛ _it ∼ N(0, 1). Practical estimation of δ, β, ξ, ξ ₀, and σ ² _a is straightforward using statistical routines for random effect probit models (e.g., ‐xtprobit‐ in Stata). In the detail, matrix δ contains δ _y, δ _gp, δ _sp the coefficients of the respective lagged values of hospital visits, GP visits, and SP visits. Matrix β contains β _gp, β _sp, β _z the coefficients of the respective values of GP visits, SP visits, and other covariates in Zit which are: health measures, the make‐ends‐meet variable, the wave dummies, and the constant. ξ is the matrix of coefficients associated with averaged values over time (Mundlak parameters) of GP visits, SP visits, health measures, and the make‐ends‐meet variable. ξ ₀ is the parameter for the “health problems in adult life.”

Simple structural coefficient tests provide useful guidance for model specification. First, H0: ρ = 0 favors the static model, while HA: ρ ≠ 0 indicates state dependence and supports the dynamic approach. Second, H0: ξ = 0 can be interpreted as a pseudo‐Hausman test for random effects since H0 indicates absence of correlation between c _i and Z _it, which clearly rejects the Mundlak‐Chamberlain device in favor of the baseline random effects probit. Third, H0: ξ ₀ = 0 rejects the influence of initial conditions, meaning that a genuinely new process is observed at the beginning of the sample.

We estimated two different models to explore two main research questions. First, we explored the determinants of hospital stays. We ran a static version of the probit model for panel data with the Mundlak‐Chamberlain device (M1), a dynamic version with initial conditions and the lagged dependant variable, and with addition of lags of ambulatory care variables (M2). Note that average partial effects (APEs) are presented instead of coefficients for the sake of comparability across models.

The validity of the dynamic panel model estimated on a balanced sample rests on the particular assumption that sample attrition is exogenous, meaning that results derived from a specific sample are independent to the reasons why some respondents dropped out of the survey. Under this assumption, estimates from the balanced and unbalanced samples should not be different. The three waves of regular panel in SHARE are reduced to two repeated observation points when one lag period is considered. As a consequence, the dynamic model cannot be estimated on an unbalanced sample, and the test procedure for exogenous attrition can only be based on the static model M1. In practice, balanced sample observations were duplicated within the working sample and the set of contemporaneous regressors is duplicated for balanced and unbalances samples. A dummy indicating whether the observation has been duplicated was added as a control variable and the model was estimated over the whole sample. Notice that time dummies were also included among the regressors. Inference on APEs between balanced and unbalanced subsamples is straightforward within this single model specification.

Our attrition test is based on a version of a Hausman test for nonresponse suggested by Nijman and Verbeek (1992). Although the authors propose the test for nondynamic models, it is standard practice to use it in a dynamic framework (e.g., Contoyannis, Jones, and Rice 2004). There are two reasons for that. First, attrition test on a nondynamic panel model is less subject to bias, as it relies on a minimum number of two periods whereas a dynamic test makes use of at least three periods (two for the panel structure and one for the lag of hospital use). Second, if attrition is endogenous, that is, if it is related to our dependent variable, then a lag of hospital use takes into account some of the reasons why attrition occurs (or attrition on observables). Fitzgerald et al. (1998) proposed a test for “dynamic attrition” and discuss its relative merit in the case for selection on unobservables.

Results

Descriptive Statistics

Figure 1 displays the value of the measures of health care use and health status for the same individuals over the four waves of SHARE. These measures are only available for the regular panel waves since wave 3 (SHARELIFE) was dedicated to life‐history data collection. The general upward trend indicates both need for care and health care consumption increase as individuals are aging. The left‐hand side graph in Figure 1 presents the distribution of the types of care used, with a wide access to GP (on average, 83 percent of the sample went to visit a GP between wave 1 and 4), and a more restricted consumption of specialist care (46.2 percent of the sample) and hospital stays (13.2 percent). Notice that the rapid surge in specialist care use (3.1 percentage points per wave) is found to be associated with the fast evolution of multimorbidity or other health measures. First difference estimates (conditional logit) indicate that after controlling for individual time‐invariant characteristics, time trends, and the usual time‐varying characteristics (financial situation, use of other health care resources: GP and hospital stays), health measures (a synthetic health index and the frailty phenotype) are strongly associated with visits to SP (p < 1 percent).

Figure 1.

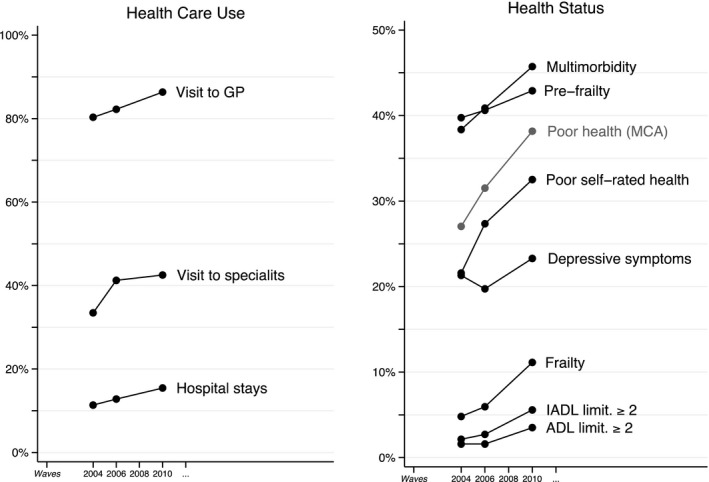
Prevalence and Incidence of Health Status and Health Care Use in Europe

Table 1 provides an overview of the average values of the variables at different points in time. Not surprisingly, care use (hospital, SP, and GP visits) is increasing in time, along with the levels of functional limitations (ADL, IADL, and frailty), depressive symptoms, and chronic conditions. Financial resources are stable over the study period.

Table 1.

Sample Description—Average Values

Variables	All Countries
	Wave 1		Wave 2		Wave 4		Overall
	Obs. (1)	Missing (2)	Obs. (1)	Missing (2)	Obs. (1)	Missing (2)	Obs. (1)	Missing (2)
Health care use
Hospital stays	0.114	0.001	0.128	0.001	0.154	0.004	0.132	0.002
Visit to GP	0.803	0.003	0.822	0.005	0.864	0.009	0.830	0.006
Visit to SP	0.334	0.003	0.412	0.005	0.425	0.009	0.391	0.006
Need for care
Fried's Frailty index [0;5]	0.662	0.049	0.718	0.069	0.947	0.098	0.776	0.072
Poor SRH	0.216	0.001	0.273	0.001	0.325	0.002	0.271	0.001
Chronic 2+	0.384	0.001	0.409	0.001	0.457	0.002	0.416	0.001
Limit. w/IADL 2+	0.021	0.001	0.027	0.001	0.056	0.002	0.035	0.001
Limit. w/ADL 2+	0.016	0.001	0.016	0.001	0.035	0.002	0.022	0.001
Depressive sympt.	0.213	0.010	0.197	0.013	0.233	0.028	0.214	0.017
Resources
Make‐ends‐meet	2.973	0.009	3.015	0.019	3.104	0.021	3.031	0.016
Initial conditions
Health problems in adult life	0.261	0.003	0.261	0.003	0.261	0.003	0.261	0.003
Other indiv. char.
Female	0.536	0.000	0.536	0.000	0.536	0.000	0.536	0.000
Years of age	63.065	0.000	65.364	0.000	69.649	0.000	66.026	0.000
Overall missing rate		0.066		0.091		0.118		0.091

(1) N = 7,562 (2) N = 9,444 individuals answer the survey at waves 1, 2, and 4. However, some respondents do not answer all the questions. Only 7,562 individuals answer all questions at all waves. As a consequence, the overall individual attrition rate is 20% (7,562/9,444) since missing observations at any wave lead to attrition in a balanced sample.

Conditional Evolution of Hospital Rates

Table 2 presents the APEs of the determinants of hospital stays. Our static model (M1) estimates suggest that increase in hospital stays between waves is essentially associated with increase in the need for care; as most health measures are significant, apart from limitations with IADL (>10 percent) or ADL (<10 percent). Progression from “good health” toward poor SRH or multimorbidity increases the risk of occurrence of hospital stays by 5 and 3 percent, respectively. The presence of more than three depressive symptoms is associated with some 1.6 percentage point increase. Progression by one point on the frailty scale [0;5] is associated with an additional risk of about 2.1 percent on average. Consumption of alternative source of care is associated with hospital stays: APEs for visits to GP and SP are of 6.5 and 11.8 percent, respectively. Finally, the Pseudo‐Hausman tests for the Mundlak‐Chamberlain device in M1 rejects the random effect assumption (χ² = 21.06; p < 1 percent), suggesting that the interpretation of the results should follow from a hypothetical “fixed effects probit model.”

Table 2.

Average Partial Effects (APEs) of the Determinants of Hospital Stays

Dep var: Hospital Stays (t)	Static Model		Dynamic Model
Explanatory Variables	APE	SE	APE	SE
Past health care use
Hospital stays (t − 1)			0.052***	0.007
Visit to GP (t − 1)			−0.002	0.013
Visit to SP (t − 1)			−0.024***	0.009
Contemporaneous altern. care
Visit to GP	0.065***	0.009	0.075***	0.014
Visit to SP	0.118***	0.006	0.121***	0.009
Contemporaneous need for care
Frailty index [0;5]	0.021***	0.004	0.025***	0.005
Poor SRH	0.049***	0.007	0.077***	0.009
Chronic 2+	0.031***	0.007	0.025***	0.009
Limit. w/IADL 2+	0.029*	0.015	0.036*	0.019
Limit. w/ADL 2+	0.011	0.017	0.027	0.022
Depressive sympt.	0.016**	0.008	0.021**	0.010
Contemporaneous resources
Make‐ends‐meet	−0.006	0.004	−0.009	0.005
Initial conditions
Health problems in adult life			0.020***	0.006
Time fixed effects
Wave 1	Ref.	Ref.
Wave 2	−0.004	0.005	Ref.	Ref.
Wave 4	0.006	0.005	0.009	0.006
(+ Mundlak device)
Tests on APEs (χ2, p‐value)
Pseudo‐Hausmann test	21.1	0.012	35.9	0.000
H0: βGPt = βSPt	476.3	0.000	238.2	0.000
H0: δGPt‐1 = δSPt‐1			7.4	0.024
Obs.	22,686		15,124

The static model explores the association between current care use variables and hospital use. The dynamic model explores the association between care use at the previous wave and current hospitalizations.

*p < .1, **p < .05, ***p < .01.

The dynamic model (M2) provides three main additional results. First, we find evidence of persistence in the dynamics of hospital stays (APE = 5 percent; p < 1 percent). Second, the static model (M1) fit can be improved by inserting lagged variables. Note that the significant influence of initial conditions in M2 increases confidence in the dynamic specification of the model as presample individual characteristics influence the dynamics of y _it. Third, M2 also indicates that although model specification should be dynamic, a lagged dependent variable is not enough to capture the full dynamic of hospital stays. We find that the presence of previous visits to specialists contributes to reduce the probability of hospitalization.

Testing for Exogenous Attrition

Table 3 presents the results of the attrition test. Notice that APEs from the same estimated equation are displayed in the column so that equality tests can be displayed on the same row. Our results indicate that each explanatory variable has statistically the same APE in both subsamples (all p‐values >10 percent). A joint test is also carried out (Wald t‐test = −1.08; p = .280) and concurs with previous individual tests that attrition in the working sample is exogenous. In addition, the APE associated with the sample dummy is not significant and indicates that conditional rates of hospital stays do not differ between subsamples. By and large, these tests suggest that attrition in the working sample does not modify the determinants of the hospital care demand function.

Table 3.

Exogenous Attrition Tests

Dep var: Hospital Stays	Average Partial Effects		Test of APEs Equality
Explanatory Variables	Selected Sample	Full Sample	Diff.	SE of Diff.	Wald t‐test	p‐value	95% CI
Health care use
Visit to GP	0.051***	0.057***	−0.006	0.007	−0.89	0.374	−0.020	0.008
Visit to SP	0.091***	0.092***	−0.002	0.004	−0.35	0.727	−0.010	0.007
Need for care
Frailty index [0;5]	0.020***	0.019***	0.001	0.002	0.58	0.563	−0.003	0.006
Poor SRH	0.041***	0.042***	−0.001	0.005	−0.19	0.852	−0.011	0.009
Multimorbidity	0.025***	0.025***	0.000	0.005	−0.06	0.954	−0.009	0.009
Limit. w/IADL 2+	0.016**	0.020**	−0.005	0.010	−0.45	0.653	−0.025	0.016
Limit. w/ADL 2+	0.006	0.009	−0.003	0.012	−0.26	0.799	−0.027	0.021
Depressive sympt.	0.012***	0.015***	−0.002	0.005	−0.44	0.657	−0.013	0.008
Resources
Make‐ends‐meet	−0.001	−0.002	0.001	0.002	0.40	0.691	−0.004	0.006
Joint model controls
Sample dummy	0.004
(+ Wave dummies)
(+ Mundlak device)
Joint test			−0.017	0.016	−1.08	0.280	−0.048	0.014
Obs.	94,769
Obs. by subsample	22,686	72,083

*p < .1; **p < .05; ***p < .01.

Conclusion

This study provides new evidence on the determinants of hospital admission rates in the general population over the recent years in Europe. We added two main contributions to the literature. First, we confirmed previous findings between healthy aging and hospitalization using a measure of frailty in the general population (Ilinca and Calciolari 2015). Second, we enhanced that model by combining the various approaches found in the literature to develop a comprehensive model that explored the dynamics of care use (Kohn and Liu 2013). We found that previous SP visits prevent future hospitalizations. This last result is of prior importance since it suggests a potential substitution effect between hospital care and specialist care. Indeed, outpatients' appointments are counted as SP visits: ambulatory specialists' visits are likely to substitute for hospital care, explaining the negative association with admissions.

Our results are consistent with previous research. Kohn and Liu (2013) have found similar persistence in the dynamics of health care use using British data. This confirmed the choice of a dynamic panel model specification. Ilinca and Calciolari (2015) have found similar association between frailty and hospitalization risks. This autonomous effect of frailty confirms that a share of the population with increasing risks of incapacity remains overlooked by means of the usual markers for incapacity, although these individuals have a higher propensity to experience hospital stays. In other words, the frailty index is an interesting potential candidate for screening subpopulations at risk who would usually fall out of the scope of prevention.

Our results support two main strategies that can be observed among European countries. The first one is essentially to promote early detection of frailty at the level of general practice to foster differential treatment in primary care. For instance, in France, a Platform for Evaluation of Frailty and Prevention of Disability has been created to identify the early signs of frailty and to design more effective interventions (Subra et al. 2012). The second strategy consists in improving coordination between actors within the health system (or integrated care), and—what is yet much less of a priority of on‐going reforms—to crucially tackle significant health inequalities in access to specialist care among the elderly. For instance, in the Netherlands, the Prevention and Reactivation Care Program and the Recovery Care Program represent personalized, integrated interventions for the prevention of functional decline after hospital stay, and the improvement of functioning for vulnerable elderly people.

Our results have important health policy implications, as they suggest that offering integrated solutions to frail elderly people would result in overall reduced hospital rates. This article brings support to the implementation of integrated solutions to prevent elderly people's hospitalizations. As frailty usually precedes dependence, health care planners show an increasing interest in developing interventions designed to prevent expensive care trajectories among frail people (De Lepeleire et al. 2009). There has been evidence that such interventions reduced the length of hospitalizations by more than 50 percent, leading to important cost savings (Brunenberg et al. 2005). Consequently, the assumption that targeting frail adults could slow down the growth of health care spending among the elderly, mainly through a reduction of hospitalization rates, is appealing and has gained wide acceptance among policy makers. The emphasis is put on the role of GPs to identify frail older people to provide early intervention and/or multidisciplinary case management (De Lepeleire et al. 2009). Further research should explore the cost‐effectiveness of interventions designed to improve frailty detection in primary care.

Supporting information

Appendix SA1: Author Matrix.

Table A1: Descriptive Statistics by Country and Waves (Average Values).