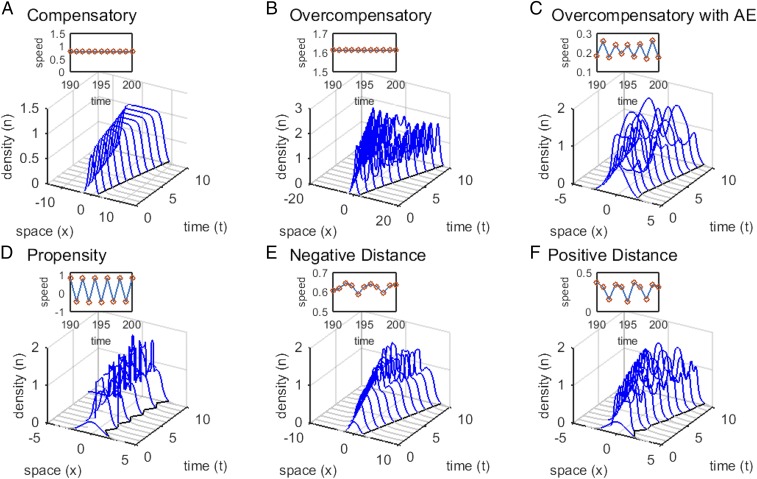
Fig. 1.

Invasion dynamics under different types of density dependence and dispersal. (A) With compensatory growth at high densities, the wave shape and invasion speed are both constant, which is true with and without low-density Allee effects (AE) (overcompensatory model: ${\sigma }^2=0.25$, $a=0$, and $r=0.9$) (SI Appendix, Fig. S1A). (B) With overcompensatory population growth and no Allee effect, population density exhibits fluctuations behind the front, but the leading edge progresses at a constant speed (overcompensatory model: ${\sigma }^2=0.25$, $a=0$, and $r=2.7$) (SI Appendix, Fig. S1A). (C) However, when overcompensation combines with low-density Allee effects, the invasion speed fluctuates (overcompensatory model: ${\sigma }^2=0.25$, $a=0.4$, and $r=2.7$) (SI Appendix, Fig. S1A). Variability in invasion speed can also occur when Allee effects combine with density dependence in (D) the proportion of dispersing offspring (SI Appendix, Fig. S1 B and C) (propensity model: $a=0.2$, $\lambda =0$, $\widehat{n}=0.9$, $p_0=0.05$, $p_{max}=1$, and $\alpha =50$) or (E and F) dispersal distance (SI Appendix, Fig. S1 B and D). In the latter model, dispersal distance (E) decreases with population density (distance model: $a=0.2$, $\lambda =0$, $\widehat{n}=0.9$, $\beta =-50$, ${\sigma }_0^2=0.05$, and ${\sigma }_{max}^2=1$) or (F) increases with density (distance model: parameters as in E except $\beta =50$). Initial population densities are either (A–C) 2 or (D–F) 0.8 times the standard normal probability density truncated at $|\text{x}|=5$.