A numerical study on stress distribution across the ankle joint: Effects of material distribution of bone, muscle force and ligaments

Abstract

Objective

The goal of this study is to develop a realistic three dimensional FE model of intact ankle joint.

Methods

Three dimensional FE model of the intact ankle joint was developed using computed tomography data sets. The effect of muscle force, ligaments and proper material property distribution of bone on stress distribution across the intact ankle joint was studied separately.

Results

Present study indicates bone material property, ligaments and muscle force have influence on stress distribution across the ankle joint.

Conclusion

Proper bone material, ligaments and muscle must be considered in the computational model for pre-clinical analysis of ankle prosthesis.

1. Introduction

Ankle arthritis and fracture cause severe, chronic pain, swelling and may result in loss of mobility at the ankle joint. Total ankle replacement (TAR) is a common method of treatment to overcome the problem related to ankle arthritis and fracture.¹ Aseptic loosening, subsidence, cysts formation, peri-prosthetic fracture and polyethylene fracture are the major issues for failures of TAR.2, 3 Development of improved ankle prosthesis has been one of the major goals over the past few years to overcome the failure related issues.⁴ However, very little improvement in design and development (in terms of material design and geometrical changes) of the ankle prosthesis has been done as compared to other prosthesis such as hip, knee and shoulder. This might be because of complexity of structure, loading and boundary conditions.

The finite element (FE) analysis evolves one of the most effective computational techniques for solving biomechanical problems.5, 6 Using FE modelling technique, the researcher can easily model the irregular geometry, complex material properties, and easily simulates the complicated boundary and loading conditions.5, 6, 7, 8 A complete FE model of intact ankle joint can help to predict the load transfer mechanism, loading situation and understand the biomechanical justification behind different treatment plans for ankle arthritis and can serves the baseline data for development of new ankle prosthesis.8, 9, 10 Before going to investigate an implanted ankle joint, it would be useful to create an accurate numerical model of intact ankle joint in combination with physiological loading conditions to quantitatively determine the equivalent stress and strain.

Stress analysis across the ankle joint was investigated earlier using FE and experimental analysis.5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 However, some of the earlier FE models of the intact ankle joint were developed with simplified material properties of bones6, 7, 8, 9, 10, 11, 12 and ligaments.6, 7, 12 The material properties of cortical and cancellous bones were considered as a single value.6, 7, 9, 11, 12 A single value of material property of cancellous bone and ligaments might not be accurate to replicate the physiological condition.¹⁷ In some earlier studies, bigger element size was used to discretize the ankle foot complex, which might be inadequate to represent complex geometry of the ankle joint.5, 10, 11, 16 The study by Ozen et al.⁶ investigated the stress distribution across the ankle joint using ligaments and muscle force. Results by Ozen et al.⁶ showed muscle force have significant influence on stress distribution across the ankle joint. However, in their model a single value of material property was considered to represent both cortical and cancellous bone, which might not be accurate to represent physiological condition.

Therefore, it has been appeared from the earlier studies that existing models have either lack of proper material distribution of bones and ligaments or they did not represent accurate geometry of bones or they did not consider the muscle force. It is anticipated that the muscle force, ligaments and material of bone have effect on load transfer and stress distribution in the different bones that forms the ankle joint. It is necessary to create a realistic three dimensional (3-D) FE model of intact ankle joint that includes all ligaments, cartilage layer, muscle forces and the heterogeneous material distribution for the cancellous bone. However, to develop a realistic FE model of an ankle joint is both challenging and time consuming, due to the intricacy of the ankle anatomy.¹⁰ The objectives of this study are (1) to develop a realistic 3-D FE model of intact ankle joint with inclusion of all musculoskeletal loading and boundary condition, proper material property distribution, (2) to investigate the effect of muscle force and ligaments on load transfer and stress distribution in the different bones that forms the ankle joint.

2. Materials and methods

In order to analyse the functions of ligaments, muscle forces and distributions of bone material properties on stress distributions around ankle joint, 3-D FE model of right intact ankle joint (combination of tibia, talus, fibula and calcaneus bone) was developed. Generation and modelling procedure of the bones, ligaments and cartilages are described in detail in below sections.

2.1. Development of the 3D FE model of bones

Three dimensional FE model of right intact ankle joint which consisting of four bones (tibia, talus, fibula and calcaneus) was developed carefully using CT-scan datasets as method mentioned by earlier studies.18, 19 At first, CT scan images of ankle-foot complex of a 35 year-old female patient were stored in.dicom format (512 × 512 pixels, pixel size: 0.803 mm and slice thickness: 1 mm) and then these datasets imported into medical image processing software to develop 3-D model of bones. In order to overcome the problem related to partial volume effect, each bone was separated by cortical and cancellous bone based on method mentioned in earlier studies.18, 19 The cancellous and cortical bone for each bony structure was separated using threshold value of bone density 1.30 g cm⁻³, where density value more than the threshold value was considered as cortical bone. Separation of cortical and cancellous bone was done in medical image processing software, accordingly, a threshold Hounsfield unit (HU) was identified based on the threshold value of bone density, 1.30 g cm⁻³.18, 19 In this present analysis threshold value of HU was found to be 1838 HU. After obtaining the 3-D solid models of all bones, further procedure such as meshing, material property distributions was done in ANSYS FE software v 17 (ANSYS, Inc., PA, USA). The 10-node tetrahedral element was used for meshing purpose. The FE model of intact ankle joint is presented in Fig. 1.

Fig. 1.

Finite element model of ankle joint showing different bones, location of ligaments, muscle force, reaction force and fixed boundary conditions.

2.2. Modelling of the cartilages

A uniform thickness of cartilage layer was considered and generated between tibia-talus, talus-calcaneus, tibia-fibula and fibula-talus bones as method described in earlier study.¹⁰ In this process an offsetting method was applied where one surface of tibia, talus, calcaneus and fibula bones was extruded first. Thereafter, Boolean operation was performed to get cartilages between all bones.¹⁰ Ten-node tetrahedral element was used for meshing purpose, where element size ranging between 0.5 mm to 1 mm was considered based on mesh convergence study. Linear elastic, homogeneous and isotropic material property was considered for cartilage material modelling, where Young’s modulus and Poisson’s ratio of 10 MPa and 0.4 considered, respectively.⁶

2.3. Generation of the ligaments

Ligament is a strong fibrous bond of tissue that connects two bones across a joint to create stability in the joint. In the present model, total sixteen ligaments were used to connect the bones; namely, Interosseous I–IV (Inte I–IV), Anterior tibiofibular (ATiFL), Posterior tibiofibular (PTiFL), Calcaneofibular (CaFL), Tibiocalcaneal (TiCa), Anterior talofibular (ATaFL), Posterior talofibular (PTaFL), Anterior tibiotalar (ATiTL), Posterior tibiotalar (PTiTL), Interosseous talocalcaneal (ITaCL), Lateral talocalcaneal (LTaCL), Medial talocalcaneal (MTaCL), Posterior talocalcaneal (PTaCL). Origin and insertion point of the each ligament was found from the earlier study.16, 20 Ligaments were modelled by using the linear spring elements. The stiffness and material values of ligaments are presented in Table 1. Each ligament was represented with four parallel springs in order to distribute accurate load at ligament bone junction.¹⁰ The FE model including all the ligaments is shown in Fig. 1.

Table 1.

Stiffness and Material Properties of Ligaments. Data taken from earlier studies.8, 24, 25, 26, 27, 28

Ligaments Represented in Models	Stiffness (N/mm)	Young’s modulus (E), MPa	Poison’s ratio(ν)
Interosseous I- IV (Inte I- IV)	400	260	0.4
Anterior tibiofibular (ATiFL)	90	160	0.49
Posterior tibiofibular (PTiFL)	90	160	0.49
Calcaneofibular (CaFL)	70	512	0.49
Tibiocalcaneal (TiCa)	122	512	0.49
Anterior talofibular (ATaFL)	90	255.5	0.49
Posterior talofibular (PTaFL)	70	216.5	0.49
Anterior tibiotalar (ATiTL)	70	184.5	0.49
Posterior tibiotalar (PTiTL)	80	99.5	0.49
Interosseous talocalcaneal (ITaCL)	70	260	0.4
Lateral talocalcaneal (LTaCL)	70	260	0.4
Medial talocalcaneal (MTaCL)	70	260	0.4
Posterior talocalcaneal (PTaCL)	70	260	0.4

2.4. Material properties of bones

The cortical bone was assumed as homogenous, isotropic and linearly elastic material. Young’s modulus and poison’s ratio for the cortical bone was assigned as 19 GPa and 0.3.⁸ The material property for the cancellous bone was assumed as heterogeneous, isotropic and linearly elastic. For the cancellous bone, location based material properties were assigned based on CT grey value.²¹ In this process, bone density (ρ in g.cm⁻³) was identified first using linear relationship between bone density and the CT grey value (in terms of HU). The following relationship was used for density calculation.

$$\rho =0.022+0.0008456\times HU$$ (1)

Two reference points were assumed to determine the density values, where lowest CT number is considered as water, that is zero corresponding to a density value of 0.022 g cm⁻³ and highest CT number is cortical bone of 2020 corresponding to highest cortical bone density of 1.73 g cm⁻³. Thereafter, following Young’s modulus-density relationship was used to determine the value of Young’s modulus.²²

$$E=4882.2{\rho }^{1.99}$$ (2)

The poison’s ratio was taken as 0.3 for the cancellous bone. Ligaments were assumed to be incompressible and their properties were presented in Table 1.

2.5. Applied loading and boundary conditions

In this present analysis double leg stance phase was considered as applied loading condition. During double leg stance phase, the primary source of loading across the ankle joint is due to the ground reaction force and the muscle force (Achilles tendon). Accordingly, the reaction force (approximately magnitude of 350 N) was applied as distributed force at the underneath surface of the calcaneus bone as shown in Fig. 1 and the muscle force (Achilles tendon) was set 75% of the total plantar pressure (approximately magnitude of 262.5 N) of the foot at the posterior extreme position of the calcaneus bone (Fig. 1).⁶ These reaction forces and muscle force were distributed on the set of nodes confined in these particular patched areas (i.e. underneath surface and posterior extreme position of the calcaneus bone). During calculation of forces the body weight was considered as 70 kg. The location and insertion point of the Achilles tendon was selected as per the earlier studies.16, 20 Proximal end of the tibia and fibula were fixed in this present model as shown in Fig. 1.⁶

2.6. Contact simulation

Contact analysis was performed to simulate the interaction between bone-to-cartilage and cartilage-to-bone. Six node surface to surface contact element was used for contact analysis. In the case of tibia-talus, talus-calcaneus and talus-fibula joint, one side of the cartilage was assumed to be fully bonded to talus bone, whereas for the other side, contact with 0.003 friction coefficient was used.⁸ For tibia-fibula joint surface connected to fibula and cartilage was considered as fixed and contact between cartilage and tibia was simulated with coefficient of friction of 0.003.⁸ For the convergence of the non-linear solution a normal contact stiffness of 10 N/mm⁻¹ and a penetration factor of 0.1 were chosen. An augmented-Lagrangian contact algorithm was used for solution of the model.

2.7. Verification and validation of the FE model

The present FE model was verified using mesh convergence study. Four intact FE models having different element sizes (total number of elements; first model: 325,531; second model: 535,834; third model: 761,055; forth model: 812,386) were generated to check whether results of FE model would depend on element size or not. Equivalent stress (von Mises stress) in the tibia, talus, fibula and calcaneus bone was chosen for convergence study. The deviation in von Mises stress in different bones was varied between 6 and 10%, when results from first two models were compared. This result was marginally reduced, when second and third model were compared. Comparison of result between the third and fourth FE models resulted in the range of deviation was reduced considerably 0.5–1%. Accordingly, third model consisting of 761,055 elements having element edge length ranging between 0.5–2 mm was chosen for further analysis.

The present FE model was also validated using earlier published data by Ozen et al.,⁶ considering same loading and boundary conditions, considering same material property distributions in the bones and other elements. The results predicted by present FE models were well comparable to earlier published data by Ozen et al.⁶ The comparison of results between present FE model and result obtained by Ozen et al.⁶ is presented in Table 2. The quantitative deviations of the stress distribution was observed, this might be due to the differences in bone geometry.

Table 2.

The Comparison of Equivalent Stress (von Mises) distribution in the different bones of intact ankle joint between the Ozen et al.⁶ FE model and the present FE model.

Bone	Peak von Mises stress
	Ozen et al.6	Present study
Tibia	5.550	5.863
Fibula	1.267	1.297
Talus	2.068	2.384
Calcaneous	3.464	4.014

2.8. Interpretation of results

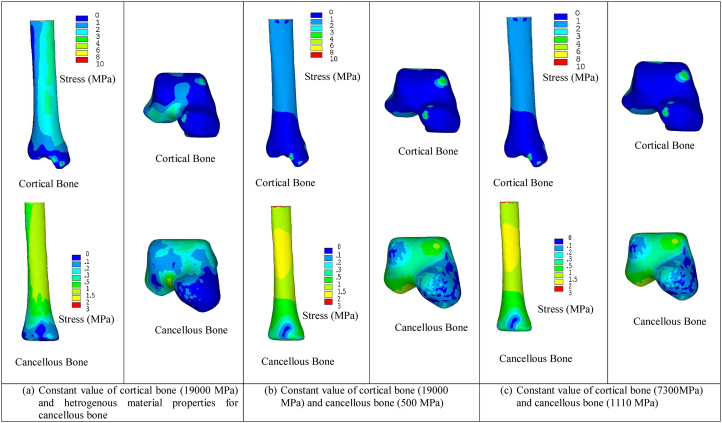
In order to understand the load transfer across the intact ankle joint, equivalent (von Mises) stress was considered as similar to the earlier studies.⁸ In earlier study showed experimentally, that von Mises stress can be considered to understand the load transfer across bones.²⁹ In this present study, the effect of material property distribution in the cortical and cancellous bone on stress distribution in the different bones (tibia, talus, fibula and calcaneus) that forms ankle joint was investigated first. In order to do this, three FE models having different material property distribution were generated. In the case of first model, the cortical bone Young’s modulus was considered as 19 GPa and heterogeneous cancellous bone material property was assigned based on Eq. (2). For second model, constant Young’s modulus of 19 GPa and 0.5 GPa was considered for both cortical and cancellous bone.⁸ In the case of third model also constant material property was considered for cortical and cancellous bone, where Young’s modulus of 7.3 GPa and 1.11 GPa was taken from earlier published study.¹⁰ Thereafter, results of three FE models were compared and select most appropriate model for further analysis. After obtaining the most appropriate model, the effects of ligaments and muscle forces on stress distribution across the intact ankle joint were studied separately. For in detailed analysis, the tibia and talus are considered to understand the effect of muscle forces, ligaments and material property of bones on load transfer across the ankle joint, since after ankle replacement these two bones are most affected as compared to other bones.

3. Results

3.1. Effect of material property distribution

The effect of material property distribution on von Mises stress in the cortical and cancellous bone is presented in Fig. 2. Results of the present study indicates that differences in stress distrubution observed due to changes in material property distribution (Fig. 2). The realistic stress distrubution was observed for model 1 (model having constant cortical bone material and heterogeneous cancellous bone material) as compared to other two models (constant material for both cortical and cancellous). However, no significant differences in stress distrubution was observed in the case of model 2 and model 3 (Fig. 2). Hence, First model was considered for further analysis, since it was proved by earlier studies that distribution of heterogeneous cancellous bone material property predictes accurate stress strain distribution across the bone.17, 30

Fig. 2.

Equivalent (von Mises) stress distribution in the cortical and cancellous bone of tibia and talus for different material properties.

3.2. Effect of muscle force and ligaments

The effect of muscle force and ligaments on load transfer (in terms of stress distribution) was studided separately and corresponding results are presented in Fig. 3, Fig. 4. For better understanding the results, stress distribution in the cortical and cancellous bone of tibia and talus, as well as sectional views are presented in Fig. 3, Fig. 4, respectively. Results form the present study indicates that the differences in stress distribution due to inclusion of muscle force and ligaments (Fig. 3, Fig. 4). The stresses observed maximum in the cortical bone of tibia, where stresses are ranging from 1 to 7 MPa, when muscle force and all ligaments were included (Fig. 3a). These stresses were reduced considerably from 1 to 5 MPa when muscle force was not included (Fig. 3a and b). The stresses were ranging from 1 to 7 MPa when ligaments were not included, however, stress patterns were observed to be different from model having inclusion of all ligaments and muscle force (Fig. 3a and c). The von Mises strees distribution in the cancellous bone of tibia was ranging from 0.1 to 2 MPa for all the three models (Fig. 3). However, the stress pattern in the cancellous bone of tibia were found to be different for all the three models (Fig. 3).

Fig. 3.

Equivalent (von Mises) stress distribution in the cortical and cancellous bone of tibia for different loading and boundary conditions (a) Inclusion of muscle force and ligaments (b) without muscle force (c) without ligaments.

Fig. 4.

Equivalent (von Mises) stress distribution in the cortical and cancellous bone of talus for different loading and boundary conditions (a) Inclusion of muscle force and ligaments (b) without muscle force (c) without ligaments.

Distributions of von Mises stress in talus bone for all the three models are shown in Fig. 4. The differences in stress distrubutions observed due to inclusion of muscle force and ligaments (Fig. 4). With the inclusion of muscle force (no ligaments) generated stresses (superior part of the talus bone) observed slightly higher and ranging from 1 to 5 MPa as compared to other two models (model having all forces and model without muscle forces), where stresses were ranging between 1 and 3 MPa (Fig. 4). Differences in stress distribution were also observed in the cancellous bone (Fig. 4). High stress 2 MPa was generated for model having all forces, whereas this stress was slightly reduced (maximum 1.5 MPa) in the case of other two models (Fig. 4).

Apart from these, the effects of each ligaments on stress distribution around ankle joint also studied in this present analysis. Present study indicates ligaments plays a crucial role in load trasfer across the ankle joint, specially in the case of tibia bone. Out of all ligaments, TiCa played a vital role in stress distribution in the tibia. Due to inclusion of TiCa ligament, the deviation in maximum von Mises stress in the cortex of the tibia was found to be more (∼12%). Results from the present study indicates muscle force and ligaments plays crucial role in load transfer across the ankle joint, these should be included in the numerical model for realistic prediction of stress distribution.

4. Discussion

The present study deals with development of a realistic 3-D FE model of ankle joint that includes four bones (tibia, talus, calcaneus and fibula), ligaments, muscle force and cartilages. The effect of muscle force, ligaments and material properties of bone on stress distribution across the ankle joint was studied separately. Previous studies on ankle and ankle foot complex considered simplified model, in terms of material, geometry and loading conditions.5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 In this present study, the authors focussed on realistic stress-strain distribution across the ankle joint using proper modelling technique, which might be beneficial for pre-clinical evaluation of ankle prosthesis and design of new ankle prosthesis.

The present FE model verified and validated using same material property of bone, and loading and boundary conditions as described earlier by Ozen et al.⁶ The maximum von Mises stress and stress distributions in the tibia, talus, fibula and calcaneus was found to be similar to the study by Ozen et al.⁶ (Table 2). However, quantitative deviation in stress distribution was observed between present study and study by Ozen et al.,⁶ this might be due to differences in geometry of bones and application of fixed boundary conditions.

Earlier studies indicate that bone material property, especially cancellous bone material has large influence on stress distribution across different bones and joints.17, 30 In earlier studies on ankle and foot ankle complex, they considered only single value of cancellous bone material, which might not be appropriate to represent physiological conditions. In this present analysis, the author considered heterogeneous material of cancellous bone and heterogeneous bone material property was assigned using power law empirical relation (Eq. (2)). This empirical relation was experimentally validated the study by Linde et al.²² for tibia. Results of the present study showed material of cancellous bone have large influence on stress distribution in the different bones (tibia, talus) that forms ankle joint (Fig. 2).

Results of the present study also indicated, apart from reaction force, muscle force has influence on stress distribution in the tibia and talus bone. A reduction of 10–50% stress at different locations of tibia and talus observed when muscle force was not included (Fig. 3, Fig. 4; sections 1-1, 2-2, 3-3). The major differences observed at the anterior-medial wall of the cortical bone of tibia (Fig. 3a and b). The differences in stress, in particular at the superior and inferior part of the talus observed, where 10–40% reduction in stress was noted (Fig. 4a and b). The differences in stress distribution also evident when ligaments were not connected to the FE model, in particular in the cortex of tibia (Fig. 3a and c; Sections 1-1, 2-2, 3-3). This might be due to maximum ligaments are connected to tibia bone as compared to talus bone. However, among all ligaments, ligament TiCa played a dominant role in load transfer across the ankle joint.

The present analysis has number of limitations and assumptions. In the present FE model no soft tissues (except ligaments and cartilages) were considered. The author assumed that material property of soft tissue is very less as compared to bone. Therefore, soft tissue might have little effect on stress distribution in different bones that forms ankle joint. The geometry of different bones and cartilages were generated based on a single CT-scan datasets and that might be useful for qualitative estimation of load transfer and stress distribution in different bones that forms ankle joint. However, for quantitative estimation of stress distribution, a multi ankle joint study, considering the effect of patient’s variability (in terms of age, sex and body weight) might be effective for better understanding the load transfer and stress distribution in different bones that forms ankle joint. The cartilages were assumed as linear elastic, isotropic and homogeneous. Time dependent material of cartilage might be more effective for better understanding the load transfer across the ankle joint. Only one loading condition, double leg stance phase was considered in this analysis. Considering other loading conditions might be more effective, for better understanding the effect of muscle and ligaments on load transfer. The main aim of this study was to determine the realistic stress distribution in the different bones that forms ankle joint. Accordingly, only four bones (tibia, fibula, talus and calcaneus) were considered. The authors assumed that other bones are far away from the ankle joint, so other bones might have little effect on load transfer and stress distribution in the different bones that forms ankle joint.

Stress distribution in the tibia and talus showed high stress was generated in the cortical bone as compared to cancellous bone (Figs. 3a and 4a). These results indicated bulk of the load transfer through the cortical bone as compared to cancellous bone. Stress at the anterior-medial wall of the cortical bone of the tibia was found to be higher and indicting load transfer through this region, when double leg stance phase was considered as loading condition (Figs. 3a and 4a). Stress distribution in the talus bone indicated load transfer through the inferior to the superior part of the talus bone (Fig. 4a). Results of the present study indicates muscle force and ligaments plays crucial role in load transfer across the ankle joint, these should be included in the numerical model for realistic prediction of stress distribution.

5. Conclusions

A realistic 3-D FE model of the ankle joint was developed based on CT- scan data and using appropriate loading and boundary conditions, and material property distribution of bones. Results of the present study indicated bulk of the load carried by the cortical bone as compared to the cancellous bone. Results of the study indicated muscle force and ligaments have large influence on load transfer and stress distribution across the ankle joint. For computational analysis, ligaments and muscle must be considered in the intact and implanted ankle model for realistic prediction of load transfer and stress-strain distribution for pre-clinical analysis of ankle prosthesis.

Conflict of interest

The authors state that with regard to the submission of this research paper, there are no financial and personal relationships with other people and organisations.