Combination therapy of cancer with cancer vaccine and immune checkpoint inhibitors: A mathematical model

Abstract

In this paper we consider a combination therapy of cancer. One drug is a vaccine which activates dendritic cells so that they induce more T cells to infiltrate the tumor. The other drug is a checkpoint inhibitor, which enables the T cells to remain active against the cancer cells. The two drugs are positively correlated in the sense that an increase in the amount of each drug results in a reduction in the tumor volume. We consider the question whether a treatment with combination of the two drugs at certain levels is preferable to a treatment by one of the drugs alone at ‘roughly’ twice the dosage level; if that is the case, then we say that there is a positive ‘synergy’ for this combination of dosages. To address this question, we develop a mathematical model using a system of partial differential equations. The variables include dendritic and cancer cells, CD4⁺ and CD8⁺ T cells, IL-12 and IL-2, GM-CSF produced by the vaccine, and a T cell checkpoint inhibitor associated with PD-1. We use the model to explore the efficacy of the two drugs, separately and in combination, and compare the simulations with data from mouse experiments. We next introduce the concept of synergy between the drugs and develop a synergy map which suggests in what proportion to administer the drugs in order to achieve the maximum reduction of tumor volume under the constraint of maximum tolerated dose.

Introduction

When cancer cells undergo necrosis, they release high mobility group box-1 (HMGB-1) which activates dendritic cells [1–3]. Activated dendritic cells (DCs) mature as APC cells and play a critical role in the communication between the innate and adaptive immune responses. Once activated, dendritic cells produce IL-12, which activates effector T cells CD4⁺ Th1 and CD8⁺ T [4, 5]. Th1 produces IL-2 which further promotes proliferation of the effector T cells. Both CD4⁺ Th1 and CD8⁺ T cells kill cancer cells [6–8]. CD8⁺ T cells are more effective in killing cancer cells, but the helper function of CD4⁺ Th1 cells improves the efficacy of tumor-reactive CD8⁺ T cells [9].

Cancer vaccines serve to enlarge the pool of tumor-specific T cells from the naive repertoire, and also to activate tumor specific T cells which are dormant [10]. GM-CSF can activate dendritic cells, and is commonly used as a cancer vaccine [11–13]. GVAX is a cancer vaccine composed of tumor cells genetically modified to secrete GM-CSF and then irradiated to prevent further cell division.

PD-1 is an immunoinhibitory receptor predominantly expressed on activated T cells [14, 15]. Its ligand PD-L1 is upregulated on the same activated T cells, but it is also expressed by some human cancer cells, such as in melanoma, lung cancer, colon cancer, and leukemia [15–17]. The complex PD-1-PD-L1 is known to inhibit T cell function [14]. Immune checkpoints are regulatory pathways in the immune system that inhibit its active response against specific targets. In the case of cancer, the complex PD-1-PD-L1 forms an immune checkpoint for T cells.

There has been much progress in recent years in developing checkpoint inhibitors, primarily PD-1 antibodies and PD-L1 antibodies [17]. Such drugs have been increasingly explored in single-agent studies for cancer treatment [16, 18]. The FDA recently approved several checkpoint inhibitors. However, because of lack of tumor-infiltrating effector T cells, many patients in clinical trials do not respond to checkpoint inhibitor treatment [18]. On the other hand, cancer vaccines have been shown to induce effector T-cells infiltration into tumors [19], although, to be fully effective, cancer vaccines have to overcome immune evasion [10]. It was recently suggested that the combination of a cancer vaccine and an immune checkpoint inhibitor may function synergistically to induce more effective antitumor immune responses [18, 20]. Clinical trials to test such combination therapies are currently ongoing [18, 20]; mouse experiments are also being conducted [21–27].

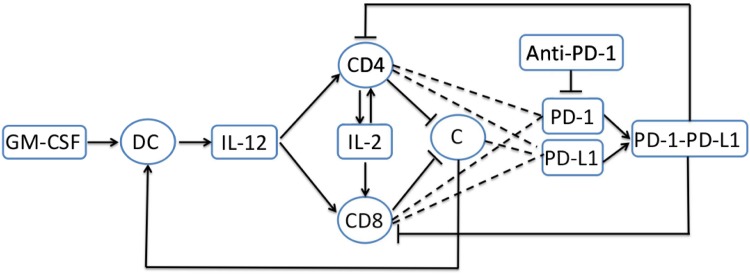
In the present paper we develop a mathematical model of treatment of cancer with a cancer vaccine combined with an immune checkpoint inhibitor; specifically, we combine GVAX and PD-1 inhibitor. In order to focus on the combination therapy of the two drugs, we consider in the model only the following variables: cancer cells (C), dendritic cells (DCs), CD4⁺ and CD8⁺ T cells, GM-CSF, PD-1, PD-L1, PD-1-PD-L1 complex, and cytokines IL-12 and IL-2. These species interact within the network shown in Fig 1. The mathematical model is based on Fig 1, and it is represented by a system of partial differential equations (PDEs). Simulations of the model are shown to be in qualitative agreement with the mouse experiments reported in [21–23]. The model is then used to explore the efficacy of the combined treatment. We introduce a specific concept of synergy between the vaccine and the PD-1 inhibitor, which is somewhat different from the usual definition of synergy. Roughly speaking, we compare the reduction in tumor size achieved by a combined therapy with amounts γ_G of GVAX and γ_A of PD-1 inhibitor to the reduction obtained by single-agent with either (1 + θ_G)γ_G or (1 + θ_A)γ_A with appropriately chosen 0 < θ_G ≤ 1 or 0 < θ_A ≤ 1. The larger the reduction in tumor size achieved by the combination therapy the larger the synergy is said to be. A specific choice of θ_G and θ_A, which takes into account potential negative side-effects of each drug, will be given as an example. We develop a synergy map in the (γ_G, γ_A)-plane. The map shows that, given γ_G, the synergy increases as γ_A increases as long as γ_A remains below a critical value γ_AG; thereafter, the synergy decreases as γ_A increases.

Fig 1. Interaction of immune cells with tumor cells.

Sharp arrows indicate proliferation/activation, blocked arrows indicate killing/blocking, and dashed lines indicate proteins on T cells. GM-CSF activates dendritic cells; activated dendritic cells produce IL-12; IL-12 activates naive CD4⁺ and CD8⁺ T cells; activated CD4⁺ T cells (Th1) produce IL-2 which induces proliferation of activated CD4⁺ and CD8⁺ T cells. Activated CD4⁺ and CD8⁺ T cells kill cancer cells. Activated CD4⁺ and CD8⁺ T cells express PD-1 and PD-L1, and cancer cells express PD-L1. The complex PD-1-PD-L1 inhibits the function of active CD4⁺ and CD8⁺ T cells.

A discrete-time mathematical model of the combination of radiotherapy with checkpoint inhibitors was developed in [28]. Mathematical models of immunotherapy with a cancer vaccine by a system of ordinary differential equations were developed earlier in [29, 30]; these models do not consider checkpoint inhibitors. In [29] it is shown that there is a positive correlation between the number of antigen presenting cells and prolonged cancer dormancy, and in [30] it is illustrated how the combined therapy can eliminate the cancer, though neither immunotherapy nor checkpoint inhibitors can do it alone. In this paper, we present for the first time a mathematical model which combines a cancer vaccine with a checkpoint inhibitor: the vaccine (GVAX) increases the pool of T cells and the checkpoint inhibitor (anti-PD-1) enables the T cells to remain fully active in killing cancer cells.

Mathematical model

The mathematical model is based on the network shown in Fig 1. The list of variables, with units, is given in Table 1.

Table 1. List of variables.

Notation	Description	units
D	density of DCs	g/cm3
T1	density of activated CD4+ T cells	g/cm3
T8	density of activated CD8+ T cells	g/cm3
C	density of cancer cells	g/cm3
NC	density of necrotic cancer cells	g/cm3
H	HMGB-1 concentration	g/cm3
G	GM-CSF concentration	g/cm3
I12	IL-12 concentration	g/cm3
I2	IL-2 concentration	g/cm3
P	PD-1 concentration	g/cm3
L	PD-L1 concentration	g/cm3
Q	PD-1-PD-L1 concentration	g/cm3
A	anti-PD-1 concentration	g/cm3

We assume that the total density of cancer cells (C), active dendritic cells (D), CD4⁺ T cells (T₁) and CD8⁺ T cells (T₈) within the tumor remains constant in space and time:

$$\begin{array}{c}\hfill C+D+T_1+T_8=\text{constant}.\end{array}$$ (1)

It is tacitly assumed that the debris of dead cells, including cancer cells undergoing necrosis or apoptosis, is quickly cleared from the tumor tissue. It is also tacitly assumed that the densities of immature dendritic cells and naive CD4⁺ and CD8⁺ T cells are constant throughout the tumor tissue.

Under the assumption Eq (1), cancer cell proliferation, and migration of immune cells into the tumor give rise to internal pressure which results in cell movement, and we assume that all the cells move with the same velocity, u; u depends on space and time. We also assume that all the cells undergo diffusion, and that all the cytokines and drugs are diffusing within the tumor.

Equation for DCs (D). When cancer cells undergo necrosis, they release HMGB-1 [1]. We can model the dynamics of the necrotic cells and of HMGB-1 by the following equations:

$$\begin{array}{ccc}& & \frac{\partial N_C}{\partial t}+\underset{\text{velocity}}{\underbrace{\nabla ·\left(\mathbf{u}{N}_C\right)}}-\underset{\text{difusion}}{\underbrace{{\delta }_{N_C}{\nabla }^2{N}_C}}=\underset{\text{derived}\text{from}\text{life}\text{cancer}\text{cells}}{\underbrace{{\lambda }_{N_{C}C}C}}-\underset{\text{removal}}{\underbrace{d_{N_C}{N}_C}},\hfill \\ & & \frac{\partial H}{\partial t}-\underset{\text{difusion}}{\underbrace{{\delta }_H{\nabla }^{2}H}}=\underset{\text{released}\text{from}\text{nerotic}\text{cancer}\text{cells}}{\underbrace{{\lambda }_{H{N}_C}{N}_C}}-\underset{\text{degradation}}{\underbrace{d_{H}H}},\hfill \end{array}$$

where λ_NCC is the rate at which cancer cells become necrotic and λ_HNC is the rate at which necrotic cells produce HMGB-1. We note that although molecules like HMGB-1, or other proteins, may be affected by the velocity $\mathbf{u}$, their diffusion coefficients are several orders of magnitude larger than the diffusion coefficients of cells; hence their velocity terms may be neglected. The degradation of HMGB-1 is fast (∼0.01/day) [31], and we assume that the removal of N_C is also fast. We can therefore approximate the two dynamical equations by the steady state equations λ_NCCC − d_NCN_C = 0 and λ_HNCN_C − d_HH = 0, so that H is proportional to C, i.e., H = constant × C.

Dendritic cells are activated by HMGB-1 [2, 3]. Hence, the activation rate of immature dendritic cell D₀ is proportional to $D_0\frac{C}{K_C+C}$, where the Michaelis-Menten law is used to account for the limited rate of receptor recycling time which occurs in the process of DCs activation. In the same way, GM-CSF, produced by the cancer vaccine, activates DCs at rate proportional to $D_0\frac{G}{K_G+G}$. Hence, the dynamics of DCs is given by

$$\begin{array}{c}\hfill \frac{\partial D}{\partial t}+\underset{\text{velocity}}{\underbrace{\nabla ·\left(\mathbf{u}D\right)}}-\underset{\text{difusion}}{\underbrace{{\delta }_D{\nabla }^{2}D}}=\underset{\text{activation}\text{by}\text{HMGB-1}}{\underbrace{{\lambda }_{DC}{D}_0\frac{C}{K_C+C}}}+\underset{\text{promotion}\text{by}\text{GM-CSF}}{\underbrace{{\lambda }_{DG}{D}_0\frac{G}{K_G+G}}}-\underset{\text{death}}{\underbrace{d_{D}D}},\end{array}$$ (2)

where δ_D is the diffusion coefficient and d_D is the death rate of DCs.

Equation for CD4⁺ T cells (T₁). Naive CD4⁺ T cells are activated by IL-12, and IL-2 induces proliferation of activated T₁ cells [4, 5]. Both processes are assumed to be inhibited by the complex PD-1-PD-L1 (Q) [14], which reduces the production of T₁ cells by a factor $\frac{1}{1+Q/K_{TQ}}$. Hence T₁ satisfies the following equation:

$$\begin{array}{ccc}\hfill \frac{\partial T_1}{\partial t}+\nabla ·\left(\mathbf{u}{T}_1\right)-{\delta }_T{\nabla }^2{T}_1& =& \underset{\text{activation}\text{by}\text{IL-12}}{\underbrace{({\lambda }_{T_1{I}_{12}}{T}_{10}\frac{I_{12}}{K_{I_{12}}+I_{12}}}}+\underset{\text{IL-2-induced}\text{proliferation}}{\underbrace{{\lambda }_{T_1{I}_2}{T}_1\frac{I_2}{K_{I_2}+I_2})}}\hfill \\ & & \times \underset{\text{inhibition}\text{by}\text{PD-1-PD-L1}}{\underbrace{\frac{1}{1+Q/K_{TQ}}}}-\underset{\text{death}}{\underbrace{d_{T_1}{T}_1}},\hfill \end{array}$$ (3)

where T₁₀ is the density of naive CD4⁺ T cells.

Equation for activated CD8⁺ T cells (T₈). IL-12 activates CD8⁺ T cells and IL-2 induces the proliferation of CD8⁺ T cells [4, 5]. Hence, similarly to the equation for T₁, T₈ satisfies the equation

$$\begin{array}{ccc}\hfill \frac{\partial T_8}{\partial t}+\nabla ·\left(\mathbf{u}{T}_8\right)-{\delta }_T{\nabla }^2{T}_8& =& \underset{\text{activation}\text{by}\text{IL-12}}{\underbrace{({\lambda }_{T_8{I}_{12}}{T}_{80}\frac{I_{12}}{K_{I_{12}}+I_{12}}}}+\underset{\text{IL-2-induced}\text{proliferation}}{\underbrace{{\lambda }_{T_8{I}_2}{T}_8\frac{I_2}{K_{I_2}+I_2})}}\hfill \\ & & \times \underset{\text{inhibition}\text{by}\text{PD-1-PD-L1}}{\underbrace{\frac{1}{1+Q/K_{TQ}}}}-\underset{\text{death}}{\underbrace{d_{T_8}{T}_8}},\hfill \end{array}$$ (4)

where T₈₀ is the density of naive CD8⁺ T cells.

Equation for tumor cells (C). Cancer cells are killed by T₁ and T₈ [6–8]. We assume a logistic growth with carrying capacity (C_M) in order to account for competition for space among the cancer cells. Hence,

$$\begin{array}{ccc}\hfill \frac{\partial C}{\partial t}+\nabla ·\left(\mathbf{u}C\right)-{\delta }_C{\nabla }^{2}C& =& \underset{\text{proliferation}}{\underbrace{{\lambda }_{C}C(1-\frac{C}{C_M})}}-\underset{\text{killing}\text{by}\text{T}\text{cells}}{\underbrace{({\eta }_1{T}_{1}C+{\eta }_8{T}_{8}C)}}-\underset{\text{death}}{\underbrace{d_{C}C}},\hfill \end{array}$$ (5)

where η₁, η₈ are the killing rates of cancer cells by T₁ and T₈, and d_C is the natural death rate of cancer cells.

Equation for GM-CSF (G). We assume that GVAX is injected intradermally every 3 days for 30 days (as in mouse experiments [21]) providing a source $\widehat{G}\left(t\right)$ of GM-CSF, which we represent by

$$\begin{array}{c}\hfill \widehat{G}\left(t\right)=\{\begin{array}{cc}{\gamma }_G\hfill & \text{if}t\le 30,\hfill \\ {\gamma }_G\times \frac{33-t}{3}\hfill & \text{if}30<t\le 33,\hfill \\ 0\hfill & \text{if}t>33.\hfill \end{array}\end{array}$$

where γ_G is the effective level of the drug; although the level of the drug varies between injections, for simplicity we take it to be constant. The concentration of GM-CSF in tissue is very small [32], and accordingly, we assume a low rate of constant source λ_G for GM-CSF. Hence G satisfies the following equation:

$$\begin{array}{ccc}\hfill \frac{\partial G}{\partial t}-{\delta }_G{\nabla }^{2}G& =& {\lambda }_G+\widehat{G}\left(t\right)-\underset{\text{degradation}}{\underbrace{d_{G}G}},\hfill \end{array}$$ (6)

where d_G is the degradation rate of GM-CSF.

Equation for IL-12 (I₁₂). IL-12 is produced by activated DCs [4, 5], so that

$$\begin{array}{ccc}\hfill \frac{\partial I_{12}}{\partial t}-{\delta }_{I_{12}}{\nabla }^2{I}_{12}& =& \underset{\text{production}\text{by}\text{DCs}}{\underbrace{{\lambda }_{I_{12}D}D}}-\underset{\text{degradation}}{\underbrace{d_{I_{12}}{I}_{12}}}.\hfill \end{array}$$ (7)

Equation for IL-2 (I₂). IL-2 is produced by activated CD4⁺ T cells (T₁) [4, 5]. Hence,

$$\begin{array}{ccc}\hfill \frac{\partial I_2}{\partial t}-{\delta }_{I_2}{\nabla }^2{I}_2& =& \underset{\text{production}\text{by}{T}_1}{\underbrace{{\lambda }_{I_2{T}_1}{T}_1}}-\underset{\text{degradation}}{\underbrace{d_{I_2}{I}_2}}.\hfill \end{array}$$ (8)

Equation for PD-1 (P), PD-L1 (L) and PD-1-PD-L1 (Q). PD-1 is expressed on the surface of activated CD4⁺ T cells and activated CD8⁺ T cells [14, 15]. We assume that the expression level of PD-1 is the same for activated CD4⁺ and CD8⁺ T cells. Hence, P is given by

$$\begin{array}{c}\hfill P={\rho }_P(T_1+T_8),\end{array}$$

where ρ_P is the ratio between the mass of one PD-1 protein to the mass of one T cell. The coefficient ρ_P is constant when no anti-PD-1 drug is injected. In that case, to a change in T = T₁ + T₈, given by $\frac{\partial T}{\partial t}$, there corresponds a change of P, given by ${\rho }_P\frac{\partial T}{\partial t}$. For the same reason, $\nabla ·\left(\mathbf{u}P\right)={\rho }_P\nabla ·\left(\mathbf{u}T\right)$ and ∇²P = ρ_P∇²T when no anti-PD-1 drug is injected. Hence, P satisfies the equation

$$\begin{array}{c}\hfill \frac{\partial P}{\partial t}+\nabla ·\left(\mathbf{u}P\right)-{\delta }_T{\nabla }^{2}P={\rho }_P[\frac{\partial (T_1+T_8)}{\partial t}+\nabla ·\left(\mathbf{u}(T_1+T_8)\right)-{\delta }_T{\nabla }^2(T_1+T_8)].\end{array}$$

Recalling Eqs (3) and (4) for T₁ and T₈, we get

$$\begin{array}{ccc}\hfill \frac{\partial P}{\partial t}+\nabla ·\left(\mathbf{u}P\right)-{\delta }_T{\nabla }^{2}P& =& {\rho }_P[({\lambda }_{T_1{I}_{12}}{T}_{10}+{\lambda }_{T_8{I}_{12}}{T}_{80})\frac{I_{12}}{K_{I_{12}}+I_{12}}\hfill \\ & & +({\lambda }_{T_1{I}_2}{T}_1+{\lambda }_{T_8{I}_2}{T}_8)\frac{I_2}{K_{I_2}+I_2}]\times \frac{1}{1+Q/K_{TQ}}\hfill \\ & & -{\rho }_P(d_{T_1}{T}_1+d_{T_8}{T}_8).\hfill \end{array}$$

When anti-PD-1 drug (A) is applied, PD-1 is depleted (or blocked) by A. In this case, the ratio $\frac{P}{T_1+T_8}$ may change. In order to include in the model both cases of with and without anti-PD-1, we replace ρ_P in the previous equation by $\frac{P}{T_1+T_8}$. Hence,

$$\begin{array}{ccc}\hfill \frac{\partial P}{\partial t}+\nabla ·\left(\mathbf{u}P\right)-{\delta }_T{\nabla }^{2}P& =& \frac{P}{T_1+T_8}[({\lambda }_{T_1{I}_{12}}{T}_{10}+{\lambda }_{T_8{I}_{12}}{T}_{80})\frac{I_{12}}{K_{I_{12}}+I_{12}}\hfill \\ & & +({\lambda }_{T_1{I}_2}{T}_1+{\lambda }_{T_8{I}_2}{T}_8)\frac{I_2}{K_{I_2}+I_2}]\times \frac{1}{1+Q/K_{TQ}}\hfill \\ & & -\frac{P}{T_1+T_8}(d_{T_1}{T}_1+d_{T_8}{T}_8)-\underset{\text{depletion}\text{by}\text{anti-PD-1}}{\underbrace{{\mu }_{PA}PA,}}\hfill \end{array}$$ (9)

where μ_PA represents the rate at which P is depleted/blocked by A.

PD-L1 is expressed on the surface of activated CD4⁺ and CD8⁺ T cells [14, 15] and on cancer cells [15, 16]. Hence, the concentration of PD-L1 (L) is proportional to (T₁ + T₈) and C:

$$\begin{array}{c}\hfill L={\rho }_L(T_1+T_8+\epsilon C),\end{array}$$ (10)

where ε depends on the specific type of tumor.

PD-L1 from T cells or cancer cells ligands to PD-1 on the plasma membrane of T cells, thus forming a complex PD-1-PD-L1 (Q) on the T cells [15, 16]. Denoting the association and disassociation rates of Q by α_PL and d_Q, respectively, we can write

$$\begin{array}{c}\hfill P+L\stackrel{{\alpha }_{PL}}{\underset{d_Q}{\rightleftharpoons }}Q,\end{array}$$ (11)

so that

$$\begin{array}{c}\hfill \frac{\partial Q}{\partial t}+\nabla ·\left(\mathbf{u}Q\right)-{\delta }_T{\nabla }^{2}Q={\alpha }_{PL}PL-d_{Q}Q.\end{array}$$

The half-life of Q is less then 1 second (i.e. 1.16 × 10⁻⁵ day) [33], and hence d_Q is very large, and we may approximate the dynamical equation by the steady state equation, α_PLPL = d_QQ, or

$$\begin{array}{c}\hfill Q=\sigma PL,\end{array}$$ (12)

where σ = α_PL/d_Q.

Equation for anti-PD-1 (A). We assume that anti-PD-1 is injected intradermally every 3 days for 30 days (as in mouse experiments [21]) providing a source $\widehat{A}\left(t\right)$ of anti-PD-1:

$$\begin{array}{c}\hfill \widehat{A}\left(t\right)=\{\begin{array}{cc}{\gamma }_A\hfill & \text{if}t\le 30,\hfill \\ {\gamma }_A\times \frac{33-t}{3}\hfill & \text{if}30<t\le 33,\hfill \\ 0\hfill & \text{if}t>33.\hfill \end{array}\end{array}$$

where γ_A is the effective level of the drug; although the level of the drug varies between injections, for simplicity we take it to be constant. The drug A is depleted in the process of blocking PD-1. Hence,

$$\begin{array}{ccc}\hfill \frac{\partial A}{\partial t}-{\delta }_A{\nabla }^{2}A& =& \widehat{A}\left(t\right)-\underset{\text{depletion}\text{through}\text{blocking}\text{PD-1}}{\underbrace{{\mu }_{PA}PA}}-\underset{\text{degradation}}{\underbrace{d_{A}A}},\hfill \end{array}$$ (13)

where μ_PA is the rate at which A is degraded in the process of blocking PD-1.

Equation for cell velocity (u): We assume that most of the tumor consists of the extracellular matrix, ECM (approximately, 0.6 g/cm³), and cancer cells (approximately, C = 0.4 g/cm³), and that the densities of D, T₁ and T₈ are approximately 4 × 10⁻⁴, 2 × 10⁻³ and 1 × 10⁻³ g/cm³, respectively (as explained in the section on parameter estimation). We further assume that all cells are approximately of the same volume and surface area, so that their diffusion coefficients are the same. For definiteness, we take the constant in Eq (1) to be 0.4034. Adding Eqs (2)–(5), we then get

$$\begin{array}{c}\hfill 0.4034\times \nabla ·\mathbf{u}=\sum _{j=2}^5\left[\text{RHS}\text{of}\text{Eq.}\right(j\left)\right].\end{array}$$ (14)

To simplify the computations, we shall assume that the tumor is spherical and denote its moving boundary (i.e. its radius) by r = R(t). We also assume that all the densities and concentrations are radially symmetric, that is, functions of (r, t), where 0 ≤ r ≤ R(t). In particular, $\mathbf{u}=u(r,t){\mathbf{e}}_r$, where ${\mathbf{e}}_r$ is the unit radial vector, and each of the equations of the form

$$\begin{array}{c}\hfill \frac{\partial X}{\partial t}+\nabla ·\left(\mathbf{u}X\right)-{\delta }_X{\nabla }^{2}X=F,\end{array}$$

with X = X(r, t), takes the form

$$\begin{array}{c}\hfill \frac{\partial X}{\partial t}+\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}uX\right)-{\delta }_X\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial X}{\partial r}\right)=F.\end{array}$$

Equation for free boundary (R): We assume that the free boundary r = R(t) moves with the velocity of cells, so that

$$\begin{array}{c}\hfill \frac{dR\left(t\right)}{dt}=u(R\left(t\right),t).\end{array}$$ (15)

Boundary conditions We assume that the naive CD4⁺ T cells and naive CD8⁺ T cells which migrated from the lymph nodes into the tumor microenvironment have constant densities ${\widehat{T}}_1$ and ${\widehat{T}}_8$ at the tumor boundary, and that they are activated by IL-12 upon entering the tumor. We represent this process by the flux conditions at the boundary r = R(t):

$$\begin{array}{c}\hfill \frac{\partial T_1}{\partial r}+{\sigma }_T\left(I_{12}\right)(T_1-{\widehat{T}}_1)=0,\frac{\partial T_8}{\partial r}+{\sigma }_T\left(I_{12}\right)(T_8-{\widehat{T}}_8)=0,\end{array}$$ (16)

where ${\sigma }_T\left(I_{12}\right)={\sigma }_0\frac{I_{12}}{I_{12}+K_{I_{12}}}$.

We impose the no-flux boundary conditions for all the remaining variables:

$$\begin{array}{c}\hfill \text{No-flux}\text{for}D(r,t),C(r,t),G(r,t),I_{12}(r,t),I_2(r,t),\\ \hfill P(r,t)\text{and}A(r,t),\text{at}r=R\left(t\right).\end{array}$$ (17)

It is tacitly assumed here that the receptors PD-1 and ligands PD-L1 become active only after the T cells are inside the tumor.

Initial conditions. We take initial values of all the variables to be constant. Later on we shall compare the simulations of the model with mouse experimental results, for 60 days. Accordingly, we take initial values whereby the average density of cancer cells has not yet increased to its steady state, 0.4 g/cm³, and, in view of Eq (1), the total density of the immune cells is initially above its steady state. We take (in unit of g/cm³):

$$\begin{array}{c}\hfill D=6\times {10}^{-4},T_1=4\times {10}^{-3},T_8=2\times {10}^{-3},C=0.3968.\end{array}$$ (18)

We assume that initially A = 0, and

$$\begin{array}{ccc}\hfill G& =& 2.61\times {10}^{-10}\text{g}/{\text{cm}}^3,I_{12}=1.8\times {10}^{-10}\text{g}/{\text{cm}}^3,I_2=4.74\times {10}^{-11}\text{g}/{\text{cm}}^3,\hfill \\ \hfill P& =& 11.2\times {10}^{-10}\text{g}/{\text{cm}}^3.\hfill \end{array}$$

These values are close to the steady state values which are computed in the section on parameter estimation.

Results

The simulations of the model were performed by Matlab based on the moving mesh method for solving partial differential equations with free boundary [34] (see the section on computational method). All the computations are done in dimensionless form, but displayed in dimensional form.

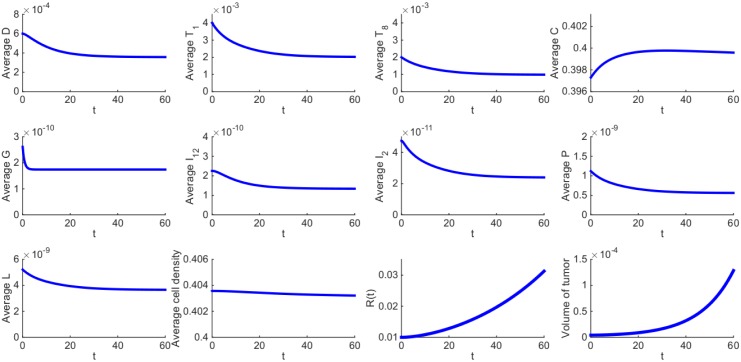
The average density or concentration of a species is defined as its total mass in the tumor divided by the tumor volume. Fig 2 shows the average concentrations of all the species of the model over a period of 60 days in the control case, that is, when no drugs are administered; the parameter values are given in Tables 2 and 3. The radius of the tumor is increasing, from 0.01 cm to 0.0313 cm. The average density of the cancer cells is initially increasing and later it stabilizes while the densities of the immune cells are first decreasing and later stabilize. Correspondingly, the concentrations of the cytokines produced by the immune system also first decrease and later stabilize. Some of the parameters in the model were estimated by assuming the immune cells and cytokines are in steady state. Their steady states in Fig 2 approximately agree with those which we assumed in estimating the parameters, thus establishing the consistency of our assumed steady-state values.

Fig 2. Average densities/concentrations of all the variables in the model in the control case (no drugs).

Figures in the first and second panels and the first figure in the third panel show the average density or concentration of each species in the model. The last three figures in the third panel show the total average density of all cells, the growth of tumor radius and the growth of tumor volume, respectively. All parameter values are the same as in Tables 2 and 3.

Table 2. Summary of parameter values.

Notation	Description	Value used	References
δD	diffusion coefficient of DCs	8.64 × 10−7 cm2day−1	[59]
δT1	diffusion coefficient of CD4+ T cells	8.64 × 10−7 cm2day−1	[59]
δT8	diffusion coefficient of CD8+ T cells	8.64 × 10−7 cm2day−1	[59]
δC	diffusion coefficient of tumor cells	8.64 × 10−7 cm2day−1	[59]
δG	diffusion coefficient of GM-CSF	9.8495 × 10−2 cm2day−1	estimated
δI12	diffusion coefficient of IL-12	6.0472 × 10−2 cm2day−1	estimated
δI2	diffusion coefficient of IL-2	9.9956 × 10−2 cm2day−1	estimated
δA	diffusion coefficient of anti-PD-1	7.85 × 10−2 cm2day−1	estimated
σ0	flux rate of T cells on the boundary	1 cm−1	[59]
λDG	activation rate of DCs by GM-CSF	20.02 day−1	[65, 66] & estimated
λDC	activation rate of DCs by tumor cells	0.364 day−1	estimated
λT1I12	activation rate of CD4+ T cells by IL-12	4.66 day−1	estimated
λT1I2	activation rate of CD4+ T cells by IL-2	0.25 day−1	estimated
λT8I12	activation rate of CD8+ T cells by IL-12	4.15 day−1	estimated
λT8I2	activation rate of CD8+ T cells by IL-2	0.25 day−1	[59]
λC	growth rate of cancer cells	0.616 day−1	[59]
λG	non-vaccine source of GM-CSF	2.23 × 10−10 g/cm3 ⋅ day	estimated
λI12D	production rate of IL-12 by DCs	5.18 × 10−7 day−1	estimated
λI2T1	production rate of IL-2 by CD4+ T cells	2.82 × 10−8 day−1	estimated
η1	killing rate of tumor cells by CD4+ T cells	11.5 day−1 ⋅ cm3/g	estmated
η8	killing rate of tumor cells by CD8+ T cells	46 day−1 ⋅ cm3/g	estimated
μPA	blocking rate of PD-1 by anti-PD-1	6.87 × 106 cm3/g ⋅ day	estimated
ρP	expression of PD-1 in T cells	2.49 × 10−7	estimated
ρL	expression of PD-L1 in T cells	5.22 × 10−7	estimated
ε	expression of PD-L1 in tumor cells	0 − 0.01*	estimated
dD	death rate of DCs	0.1 day−1	[59]
dT1	death rate of CD4+ T cells	0.197 day−1	[59]
dT8	death rate of CD8+ T cells	0.18 day−1	[59]
dC	death rate of tumor cells	0.17 day−1	[59]
dG	degradation rate of GM-CSF	1.28 day−1	[65]
dI12	degradation rate of IL-12	1.38 day−1	[59]
dI2	degradation rate of IL-2	2.376 day−1	[59]
dA	degradation rate of anti-PD-1	0.0462 day−1	[42]

* In the simulations we took ε = 0.01.

Table 3. Summary of parameter values.

KG	half-saturation of GM-CSF	1.74 × 10−9 g/cm3	[65]
KC	half-saturation of tumor cells	0.4 g/cm3	[59]
KI12	half-saturation of IL-12	1.5 × 10−10 g/cm3	[59]
KI2	half-saturation of IL-2	2.37 × 10−11 g/cm3	[59]
KT1	half-saturation of CD4+ T cells	2 × 10−3 g/cm3	estimated
KT8	half-saturation of CD8+ T cells	1 × 10−3 g/cm3	estimated
$K_{TQ}^{\prime }$	inhibition of function of T cells by PD-1-PD-L1	1.365 × 10−18 g/cm3	estimated
D0	density of immature DCs	2 × 10−5 g/cm3	[59]
T10	density of naive CD4+ T cells	4 × 10−4 g/cm3	estimated
T80	density of naive CD8+ T cells	2 × 10−4 g/cm3	estimated
CM	carrying capacity of cancer cells	0.8 g/cm3	[59]
${\widehat{T}}_1$	density of CD4+ T cells from lymph node	4 × 10−3 g/cm3	estimated
${\widehat{T}}_8$	density of CD8+ T cells from lymph node	2 × 10−3 g/cm3	estimated
γG	source of GM-CSF from the vaccine	1 × 10−10 g/cm3 ⋅ day*	estimated
γA	source of anti-PD-1	1 × 10−10 g/cm3 ⋅ day*	estimated

* Values used in sensitivity analysis.

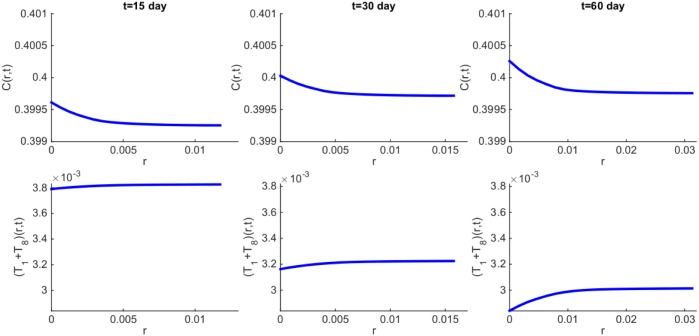
We can also simulate the spatial distribution of each of the variables. Fig 3 shows the distribution of cancer cells and T cells (T₁ + T₈) at times t = 15, 30, 60 days. We see that the density of T cells increases toward the boundary; this is a result of the influx of T cells from the lymph nodes. Correspondingly, the density of cancer cells decreases toward the boundary. In our model, we tacitly assumed avascular conditions, since we wanted to focus primarily on the difference between control and treatment. Since, however, the tumor radius reaches approximately 313 μm at day 60, hypoxic conditions may actually reduce the cancer cells’ density at the core of the tumor (both in control and treatment).

Fig 3. Spatial distribution of density of cancer cells and T₁ + T₈ cells at time t = 15, 30, 60 days.

All parameter values are the same as in Fig 2.

In Figs 2 and 3, we have taken ε = 0.01. Some cancer cells may express more or less PD-L1 [17, 35–37]. By decreasing or increasing ε, the radius of the tumor will decrease or increase, respectively, but the profiles of the densities/concentrations remain qualitatively the same (not shown here).

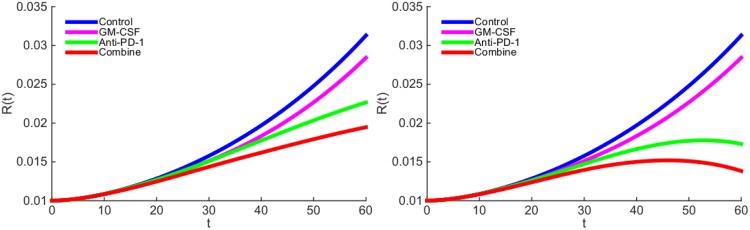
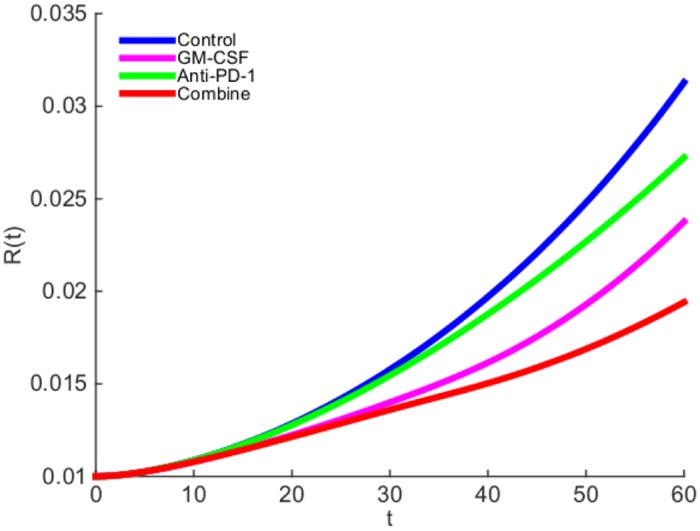
We next proceed to explore the effect of treatment with GM-CSF-secreting vaccine (GVAX) and anti-PD-1 drug. We are unable to make a direct connection between the levels of drugs administered to the patient, and their ‘effective strengths’ γ_G and γ_A in the model, since these data are not available. Based on the estimate of the concentration of GM-CSF in normal healthy tissue (see Parameter Estimations for Eq (6)), we chose the order of magnitude of GVAX to be 10⁻¹⁰ (g/cm³ ⋅ day). The order of magnitude for anti-PD-1 drug (γ_A) is chosen so as to get the best agreement with the mouse experiments. In Fig 4(a), the ‘effective strength’ of the vaccine is given by γ_G = 0.87 × 10⁻¹⁰ g/cm³ ⋅ day and the ‘effective strength’ of the anti-PD-1 is given by γ_A = 2 × 10⁻¹⁰ g/cm³ ⋅ day. We see that, as a single-agent, anti-PD-1 is more effective than GVAX, and with the combined therapy the tumor radius is still increasing. This is in agreement with the mouse experiments reported in Fig 1-(A) (with melanoma) in [21], and Figs 3-(b) (with colon carcinoma) and 3-(c) (with melanoma) in [22].

Fig 4. The growth of tumor radius R(t) during the administration of GM-CSF-secreting vaccine and anti-PD-1 drug.

(a) GM-CSF-secreting vaccine is administered at rate γ_G = 0.87 × 10⁻¹⁰ g/cm³ ⋅ day and anti-PD-1 drug is administered at rate γ_A = 2 × 10⁻¹⁰ g/cm³ ⋅ day. (b) GM-CSF-secreting vaccine is administered at rate γ_G = 0.87 × 10⁻¹⁰ g/cm³ ⋅ day and anti-PD-1 drug is administered at rate γ_A = 3 × 10⁻¹⁰ g/cm³ ⋅ day.

In Fig 4(b), we increased γ_A by a factor 3/2. As a result, the tumor radius begins to decrease around day 50, even when administering anti-PD-1 as single-agent. This is in agreement with mouse experiments (with colon carcinoma) reported in Fig 1-(D) of [23].

In Fig 4(a), GM-CSF-secreting vaccine alone did not reduce the tumor radius as much as anti-PD-1 alone. However, if we increase the strength of the vaccine and decrease the anti-PD-1, taking for example, γ_G = 3.84 × 10⁻¹⁰ g/cm³ ⋅ day and γ_A = 1 × 10⁻¹⁰ g/cm³ ⋅ day, we then find that the vaccine decreases the tumor radius more than anti-PD-1 does; this is shown in Fig 5, and it is in agreement with mouse experiments (with melanoma) reported in Fig 1-(B) of [23].

Fig 5. The growth of tumor radius R(t) during the administration of GM-CSF-secreting vaccine and anti-PD-1 drug.

GM-CSF-secreting vaccine is administered at rate γ_G = 3.84 × 10⁻¹⁰ g/cm³ ⋅ day and anti-PD-1 drug is administered at rate γ_A = 1 × 10⁻¹⁰ g/cm³ ⋅ day.

The results of Figs 4 and 5 show that a combination therapy of GVAX and anti-PD-1 in appropriate amounts could significantly slow the growth of a tumor.

There is some uncertainty in the estimates of some of the parameters of the model. With somewhat different choices of these parameters, the simulation results will change quantitatively, and sensitivity analysis indicates the direction and intensity of the change (see the section on sensitivity analysis). In particular, the choice of γ_G and γ_A will affect the relative reduction in the growth of the tumor radius. In Figs 4 and 5 we made specific choices of γ_G and γ_A, in order to get simulations that agree with experimental results.

We next consider combination therapy for any values of GVAX and anti-PD-1. We define the efficacy of the combination therapy with (γ_G, γ_A) by the formula:

$$\begin{array}{c}\hfill E({\gamma }_G,{\gamma }_A)=\frac{R_{60}(0,0)-R_{60}({\gamma }_G,{\gamma }_A)}{R_{60}(0,0)},\end{array}$$

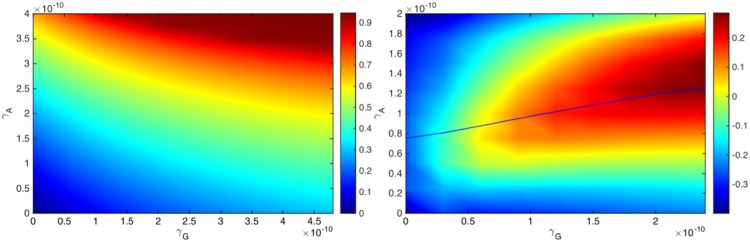
where R₆₀ = R₆₀(γ_G, γ_A) represents the tumor radius computed at day 60. If the tumor radius at day 60, R₆₀(γ_G, γ_A), is smaller than the radius in the control case, R₆₀(0, 0), then the efficacy is a positive number, and its value is between 0 and 1 (or between 0% and 100%); the efficacy increases to 1 (or to 100%) when the tumor radius R₆₀(γ_G, γ_A) decreases to 0 by day 60. Fig 6(a) is the efficacy map of the combined therapy with γ_G in the range of 0 − 4.8 × 10⁻¹⁰) g/cm³ ⋅ day and γ_A in the range of 0 − 4 × 10⁻¹⁰ g/cm³ ⋅ day. The color column in Fig 6(a) shows the efficacy for any pair of (γ_G, γ_A); the efficacy is positive, and its maximum is 0.95 (95%). We see that an increase in either γ_G or γ_A improves the efficacy of the treatment.

Fig 6. Drug efficacy map and synergy map.

(a) Efficacy map: The color column shows the efficacy E(γ_G, γ_A) when γ_G varies between 0 − 4.8 × 10⁻¹⁰ g/cm³ ⋅ day and γ_A varies between 0 − 4 × 10⁻¹⁰ g/cm³ ⋅ day. (b) Synergy map: The color column shows the synergy σ(γ_G, γ_A) when γ_G varies between 0 − 2.4 × 10⁻¹⁰ g/cm³ ⋅ day and γ_A varies between 0 − 2 × 10⁻¹⁰ g/cm³ ⋅ day. For a given γ_G, the optimal synergy of the combined therapy (γ_G, γ_A) occurs when (γ_G, γ_A) lies on the solid curve.

Early stage clinical trials consider the safety of each of the drugs, GVAX and anti-PD-1, separately. In the GVAX treatment of patients with pancreatic cancer, no dose-limiting toxicity or minimal toxicity was observed [38–40]. On the other hand, in treatment with anti-PD-1, mild to moderate toxicity (grades 1 and 2) was observed in melanoma [41, 42]. In non-small-cell lung cancer, 14% of the patients were observed to have more severe toxicity (grades 3 and 4) [43]. Based on these observations we conclude that anti-PD-1 causes more toxicity than GVAX. However, clinical trials on the safety and efficacy of the combined drugs are limited [23, 44, 45].

The amount of drug in clinical trials is constrained by the maximum tolerated dose (MTD). In combination therapy this constraint may depend on the proportion between the amounts of the drugs. We note that there is a large literature on the trade-off between efficacy and toxicity [46–49]. Here we consider, as an example, two treatments, $({\gamma }_G^{*},{\gamma }_A^{*})$ and $({\gamma }_G^{**},{\gamma }_A^{**})$, with ${\gamma }_G^{*}>{\gamma }_G^{**}$ and ${\gamma }_A^{*}<{\gamma }_A^{**}$, where both satisfy the MTD requirement. The question is then which of the two treatments is more effective in reducing the tumor volume. We can use the efficacy map to address such a question. We illustrate this in one special case.

We compare treatment of combination (γ_G, γ_A) with monotherapy GVAX and monotherapy anti-PD-1. For monotherapy with GVAX, we take (1 + θ_G)γ_G, and for monotherapy with anti-PD-1 we take (1 + θ_A)γ_A, with θ_A < θ_G, to reflect the higher toxicity associated with anti-PD-1. If E(γ_G, γ_A) is larger than both E((1 + θ_G)γ_G, 0) and E(0, (1 + θ_A)γ_A), then we say that the synergy for the combination (γ_G, γ_A) is positive, and otherwise, we say that the synergy is negative. More generally, we define the synergy σ = σ(γ_G, γ_A) by the formula:

$$\begin{array}{c}\hfill \sigma ({\gamma }_G,{\gamma }_A)=\frac{E({\gamma }_G,{\gamma }_A)}{\text{max}\{E((1+{\theta }_G){\gamma }_G,0),E(0,(1+{\theta }_A){\gamma }_A)\}}-1.\end{array}$$ (19)

Thus σ(γ_G, γ_A) > 0 (positive synergy) if the combination (γ_G, γ_A) reduces tumor growth more than either one of the single agents with (1 + θ_G)γ_G or (1 + θ_A)γ_A. Negative synergy occurs in the reverse case where instead of a combination therapy with (γ_G, γ_A) we achieve better reduction of the tumor radius R₆₀ if we apply only one drug, (1 + θ_G)γ_G or (1 + θ_A)γ_A. The above concept of synergy is somewhat different from the usual definitions of synergy. For definiteness we take θ_G = 1 and γ_A = 0.5, but this choice, which is somewhat arbitrary, could be made more precise as more clinical data become available.

Fig 6(b) is the synergy map for (γ_G, γ_A) in the same range as in Fig 6(a); the color column shows the synergy σ(γ_G, γ_A), with values that vary from -0.38 to 0.28.

We first note that the synergy is negative if γ_G < 0.2 × 10⁻¹⁰ g/cm³ ⋅ day. The reason is the following: if γ_G is small then the numbers of T cells is also small, so instead of introducing a drug γ_A which blocks the relatively small number of PD-1, it is more effective to increase the number of T cells by increasing γ_G, i.e. E(2γ_G, 0) > E(γ_G, γ_A).

Next, for any fixed γ_G, as seen in Fig 6(b), the synergy first increases with γ_A and then decreases. In order to explain this occurrence, we note that with γ_G fixed, the number of T cells that arrive into the tumor microenvironment is limited, and so is the number of their PD-1. Thus, in order to block the PD-1 there is a need for only a limited amount of anti-PD-1 drug; i.e. it is ‘wasteful’ to administer too much of γ_A. We conclude that the maximum synergy is achieved when the amount of γ_A is appropriately dependent on the amount of γ_G, as indicated by the solid curve shown in Fig 6(b).

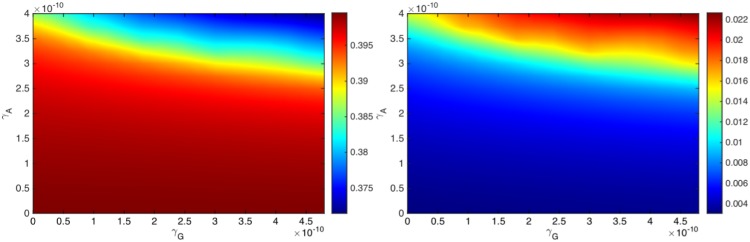
Fig 7 shows that as the amounts of γ_G and γ_A increase the average density of T cells (T₁ + T₈) increases, and correspondingly the average density of cancer cells decreases. We also see that the density of T cells shown in the color column increases approximately by a factor of 6, whereas the density of cancer cells decreases approximately by a factor of 1.075. The proportion of these changes (i.e. 5/0.075) is similar to the proportion of densities of cancer cells to T cells.

Fig 7. Average densities of cancer cells and T cells.

(a) The average density of cancer cells (C), and (b) the average density of T cells (T₁ + T₈), under the combination of the drugs with (γ_G, γ_A), where γ_G varies between 0 − 4.8 × 10⁻¹⁰ g/cm³ ⋅ day and γ_A varies between 0 − 4 × 10⁻¹⁰ g/cm³ ⋅ day.

Conclusion

The introduction of immune checkpoint inhibitors has been a very promising approach to cancer treatment. Blockage of the programmed death PD-1/PD-L1 is increasingly explored in single-agent studies [16, 18]. However, because of the lack of tumor-infiltrating effector T cells, many patients do not respond to checkpoint inhibitor treatment as single-agent [18]. On the other hand, cancer vaccines have been shown to induce effector T-cells infiltration into tumors [19], although, to be fully effective, cancer vaccines have to overcome immune evasion [10]. It was recently suggested that the combination of a cancer vaccine and an immune checkpoint inhibitor may function synergistically to induce more effective antitumor immune response [18, 20]. Clinical trials to test such combinations are currently ongoing [18, 20].

In the present paper we developed a mathematical model to study the efficacy of the combination of a GM-CSF-secreting cancer vaccine (GVAX) and an anti-PD-1 drug, and to address the following question: at what proportion should the two drugs be administered in order to achieve the best efficacy when the amount of drugs is limited by MTD. The mathematical model is represented by a system of partial differential equations, based on the interactions among cancer cells, dendritic cells, CD4⁺ and CD8⁺ T cells, cytokines IL-12 and IL-2, GM-CSF, PD-1, PD-L1, PD-1-PD-L1 complex and anti-PD-1. Simulations of the model are shown to be in qualitative agreement with mouse experiments [21–23].

The cancer vaccine and the anti-PD-1 work in collaboration: The vaccine increases the number of tumor-infiltrating effector T cells and the anti-PD-1 ensures that these cells remain active. Given a fixed amount γ_G of the vaccine and γ_A of the anti-PD-1, it is important to estimate the level of synergy between these amounts in order to administer them in the most effective proportion. We introduced a specific concept of synergy σ(γ_G, γ_A) and developed accordingly a synergy map in Fig 6(b). The map shows that if γ_G is small, single-agent treatment (with γ_A = 0) is the best treatment. Fig 6(b) also shows that, for any γ_G, there is a unique value γ_AG, such that the synergy increases as γ_A increases as long as γ_A remains smaller than γ_AG, but the synergy decreases as γ_A increases above γ_AG; the points (γ_G, γ_AG) form the solid curve shown in Fig 6(b). We suggest that for optimal efficacy under MTD constraint, the level of dosage of anti-PD-1 (γ_A) should be related to the level of dosage of GVAX (γ_G) by setting γ_A = γ_AG, as indicated by the solid curve in Fig 6(b).

The mathematical model presented in this paper has several limitations:

1. In order to focus on the combined therapy of a cancer vaccine and an anti-PD-1 drug, we did not include some other important cells and cytokines that are found in the tumor microenvironment, such as T regulatory cells, macrophages, endothelial cells, and IL-10, IL-6 and TGF-β. We also did not include blood vessels and oxygen, thus assuming that the tumor is avascular. We tacitly assumed that the effect of these omissions is not significant in comparing the results of therapy to no therapy.

2. We assumed that the densities of immature, or naive, immune cells remain constant throughout the progression of the cancer and that dead cells are quickly removed from the tumor.

3. In estimating parameters we made a steady state assumption in some of the differential equations.

4. In the definition of synergy, and in the synergy map, we included in a crude way the fact that anti-PD-1 causes more toxicity than GVAX. Our aim was to develop a concept that will take account not only of efficacy but also of toxicity. For this reason we compared the treatment benefits for combination (γ_G, γ_A) with the single agents (2γ_G, 0) and (0, 1.5γ_A).

5. We did not make any direct connection between drugs administered to the patient, and their ‘effective strengths’ γ_G and γ_A, as they appear in the differential equations, since these data are not available. The order of magnitude of GVAX (10⁻¹⁰) was based on the estimate of the concentration of GM-CSF in normal healthy tissue (see Parameter Estimations for Eq (6)). We simulated the model with different orders of magnitude for anti-PD-1 drug (γ_A) and found the best agreement with the mouse experiments (in Figs 4 and 5) when γ_A is also of order of magnitude 10⁻¹⁰.

6. Although our mathematical model does not presume any geometric form of the tumor, for simplicity, the simulations have been carried out only in the case of a spherical tumor. We note however that spherical cancer models have been used in research as an intermediate between in vitro cancer line cultures and in vivo cancer [50]. Furthermore, spheroids mirror the 3D cellular context and therapeutically relevant pathophysiological gradient of in vivo tumors [51].

Clinical data on efficacy and toxicity are quite limited at this time. Our model should be viewed as setting up a computational framework, to address the question of optimal efficacy in combination therapy with cancer vaccine and checkpoint inhibitor.

Materials and methods

Parameter estimation

Half-saturation. In an expression of the form $Y\frac{X}{K_X+X}$ where Y is activated by X, the half-saturation parameter K_X is taken to be the approximate steady state concentration of species X.

Diffusion coefficients. By [52], we have the following relation for estimating the diffusion coefficients of a protein p:

$$\begin{array}{c}\hfill {\delta }_p=\frac{M_V^{1/3}}{M_p^{1/3}}{\delta }_V,\end{array}$$

where M_V and δ_V are respectively the molecular weight and diffusion coefficient of VEGF, M_p is the molecular weight of p, and M_V = 24kDa [53] and δ_V = 8.64 × 10⁻² cm²day⁻¹ [54]. Since M_I2 = 15.5kDa, M_I12 = 70kDa, M_G = 16.2kDa [55] and M_A = 32kDa [56], we get δ_I2 = 9.9956 × 10⁻² cm²day⁻¹, δ_I12 = 6.0472 × 10⁻² cm²day⁻¹, δ_G = 9.8495 × 10⁻² cm²day⁻¹, and δ_A = 7.85 × 10⁻² cm²day⁻¹.

Eq (2): The number of DCs in various organs (heart, kidney, pancreas and liver) in mouse varies from 1.1 × 10⁶ cells/cm³ to 6.6 × 10⁶ cells/cm³ [57]. Mature DCs are approximately 10 to 15 μm in diameter [58]. Accordingly, we estimate steady states of DCs by K_D = 4 × 10⁻⁴ g/cm³. We assume that the density of immature DCs is smaller than the actived DCs, and take $D_0=\frac{1}{20}{K}_D=2\times {10}^{-5}$ g/cm³. We also assume that the activation of DCs by GM-CSF-secreting vaccine is more effective than their activation by NCs-secreted HMGB-1, and take ${\lambda }_{DG}\frac{G}{K_G+G}=10{\lambda }_{DC}\frac{C}{K_C+C}$. From the steady state of Eq (2) in the control case (with no drug), we get

$$\begin{array}{c}\hfill {\lambda }_{DC}{D}_0·\frac{C}{K_C+C}+{\lambda }_{DG}{D}_0·\frac{G}{K_G+G}-d_{D}D=0,\end{array}$$

where d_D = 0.1/day [59], D₀ = 2 × 10⁻⁵ g/cm³, D = K_D = 4 × 10⁻⁴ g/cm³, C = K_C = 0.4 g/cm³, and $G={\widehat{K}}_G=1.74\times {10}^{-10}$ g/cm³ and K_G = 1.74 × 10⁻⁹ g/cm³ (${\widehat{K}}_G$ and K_G are estimated together with other estimates of Eq (6)). Hence λ_DC = 0.364/day and λ_DG = 20.02/day.

Eq (3): The number of lymphocytes is approximately twice the number of DCs [57]. T cells are approximately 14 to 20 μm in diameter. Assuming that the number of Th1 cells is 1/4 of the number of lymphocytes, we estimate the steady state density of Th1 cells by K_T = 2 × 10⁻³ g/cm³. We assume the density of naive CD4⁺ T cells to be less than the density of Th1, and take $T_{10}=\frac{1}{5}{K}_T=4\times {10}^{-4}$ g/cm³. We also assume that in steady state, Q/K_TQ = 2 (K_TQ is estimated together with other estimates of Eqs (9)–(12)). From the steady state of Eq (3), we get

$$\begin{array}{c}\hfill ({\lambda }_{T_1{I}_{12}}{T}_{10}·\frac{1}{2}+{\lambda }_{T_1{I}_2}{T}_1·\frac{1}{2})·\frac{1}{3}-d_{T_1}{T}_1=0,\end{array}$$

where T₁₀ = 4 × 10⁻⁴ g/cm³, T₁ = K_T1 = 2 × 10⁻³ g/cm³, and, by [59], λ_T1I2 = 0.25/day and d_T1 = 0.197/day. Hence λ_T1I12 = 4.66/day.

Eq (4): The CD4/CD8 ratio in the blood is 2:1. We assume a similar ratio in the tissue, and take $T_{80}=\frac{1}{2}{T}_{10}=2\times {10}^{-4}$ g/cm³. We also take the steady state of T₈ to be half of the steady state of T₁, i.e., $K_{T_8}=\frac{1}{2}{K}_{T_1}=1\times {10}^{-3}$ g/cm³. From the steady state equation of Eq (4), we get

$$\begin{array}{c}\hfill ({\lambda }_{T_8{I}_{12}}{T}_{80}·\frac{1}{2}+{\lambda }_{T_8{I}_2}{T}_8·\frac{1}{2})·\frac{1}{3}-d_{T_8}{T}_8=0,\end{array}$$

where T₈₀ = 5 × 10⁻⁵ g/cm³, T₈ = K_T8 = 1 × 10⁻³ g/cm³, and, by [59], λ_T8I2 = 0.25/day and d_T8 = 0.18/day. Hence λ_T1I12 = 4.15/day.

Eq (5): We take d_C = 0.17 day⁻¹ and C_M = 0.8 g/cm³ [59]. In the absence of immune responses and anti-tumor drugs, the tumor grows according to

$$\begin{array}{c}\hfill \frac{dC}{dt}={\lambda }_{C}C(1-\frac{C}{C_M})-d_{C}C,\end{array}$$ (20)

and with immune response, the tumor grows according to

$$\begin{array}{c}\hfill \frac{dC}{dt}={\lambda }_{C}C(1-\frac{C}{C_M})-({\eta }_1{T}_1+{\eta }_8{T}_8)C-d_{C}C.\end{array}$$ (21)

Mouse experiments show that the tumor volume on average doubles within 5-15 days [21–23]. Assuming a linear growth

$$\begin{array}{c}\hfill \frac{dC}{dt}={\lambda }_{0}C,\text{where}{\lambda }_0>0,\end{array}$$

during the volume doubling time, we conclude from Eq (21) that

$$\begin{array}{c}\hfill {\lambda }_{C}C(1-\frac{C}{C_M})-({\eta }_1{T}_1+{\eta }_8{T}_8)C-d_{C}C={\lambda }_{0}C.\end{array}$$ (22)

where ${\lambda }_0\in (\frac{\text{ln}2}{15},\frac{\text{ln}2}{5})$. We assume that with no immune responses

$$\begin{array}{c}\hfill \frac{dC}{dt}=2{\lambda }_{0}C,\end{array}$$

so that, by Eq (20), we get

$$\begin{array}{c}\hfill {\lambda }_{C}C(1-\frac{C}{C_M})-d_{C}C=2{\lambda }_{0}C.\end{array}$$ (23)

We take λ₀ = 0.069/day, and assume that in steady state of Eqs (20) and (21), C is approximately 0.4 g/cm³, so that from Eq (23) we get

$$\begin{array}{c}\hfill \frac{1}{2}{\lambda }_C-d_C=2{\lambda }_0,\end{array}$$

or λ_C = 0.616/day. From Eqs (23) and (22), we get η₁T₁ + η₈T₈ = λ₀. Noting that T₈ cells kill cancer cells more effectively than T₁ cells, we take η₈ = 4η₁, so that ${\eta }_1=\frac{{\lambda }_0}{T_1+4T_8}=11.5$ cm³/g ⋅ day and η₈ = 46 cm³/g ⋅ day (with T₁ = K_T1 = 2 × 10⁻³ g/cm³ and T₈ = K_T8 = 1 × 10⁻³ g/cm³ as in the estimates for Eqs (3) and (4)).

Eq (6): With no drugs, the steady state plasma concentration of GM-CSF is $G={\widehat{K}}_G=1.74\times {10}^{-10}$ g/cm³ [60]. The half-life of GM-CSF is 13 hours [61], i.e, 0.54 day, so that $d_G=\frac{\text{ln}2}{0.54}=1.28$/day. From the steady state of Eq (6) (with no drugs), we get ${\lambda }_G=d_{G}G=d_G{\widehat{K}}_G=2.23\times {10}^{-10}$ g/cm³ ⋅ day. But when the GM-CSF-secreting vaccine is administered, the concentration of GM-CSF shoots up, and we assume that at steady states it reaches the level of $G=K_G=10{\widehat{K}}_G=1.74\times {10}^{-9}$ g/cm³.

Eq (7): From the steady state of Eq (7), we get λ_I12DD − d_I12I₁₂ = 0, where d_I12 = 1.38/day [59] and I₁₂ = K_I12 = 1.5 × 10⁻¹⁰ g/cm³ [59], and D = K_D = 4 × 10⁻⁴ g/cm³. Hence, λ_I12D = 5.18 × 10⁻⁷/day.

Eq (8): From the steady state of Eq (8), we get λ_I2T1T₁−d_I2I₂ = 0, where d_I2 = 2.376/day [59] and I₂ = K_I2 = 2.37 × 10⁻¹¹ g/cm³ [59], and T₁ = K_T1 = 2 × 10⁻³ g/cm³. Hence, λ_I2T1 = 2.82 × 10⁻⁸/day.

Eqs (9)–(12): In order to estimate the parameter K_TQ (in Eqs (3) and (4)), we need to determine the steady state concentrations of P and L in the control case (no drugs). To do that, we need to estimate ρ_P and ρ_L. By [62], the mass of one PD-1 protein is m_P = 8.3 × 10⁻⁸ pg = 8.3 × 10⁻²⁰ g, and by [63] the mass of one PD-L1 is m_L = 5.8 × 10⁻⁸ pg = 5.8 × 10⁻²⁰ g. We assume that the mass of one T cell is m_T = 10⁻⁹ g. By [14], there are 3000 PD-1 proteins and 9000 PD-L1 proteins on one T cell (T₁ or T₈). Since ρ_PT is the density of PD-1 (without anti-PD-1 drug), we get ${\rho }_P=3000\times \frac{m_P}{m_T}=\frac{3000\times (8.3\times {10}^{-20})}{{10}^{-9}}=2.49\times {10}^{-7}$ and ${\rho }_L=9000\times \frac{m_L}{m_T}=\frac{9000\times (5.8\times {10}^{-20})}{{10}^{-9}}=5.22\times {10}^{-7}$.

In steady state, T₁ = 2 × 10⁻³ g/cm³ and T₈ = 1 × 10⁻³ g/cm³. Hence, in steady state,

$$\begin{array}{ccc}\hfill P& =& {\rho }_P(T_1+T_8)=(2.49\times {10}^{-7})\times (2\times {10}^{-3}+1\times {10}^{-3})=7.47\times {10}^{-10}\text{g}/{\text{cm}}^3.\hfill \end{array}$$

The parameter ε in Eq (10) depends on the type of cancer; many cancer cells, but not all, express PD-L1 [17, 35–37]. Accordingly, we assume ε varies in the interval 0-0.01, but in the simulations we take ε = 0.01. Then, from Eq (10), we get

$$\begin{array}{ccc}\hfill L& =& {\rho }_L(T_1+T_8+\epsilon C)=(5.22\times {10}^{-7})\times [2\times {10}^{-3}+1\times {10}^{-3}+0.01\times 0.4]\hfill \\ & =& 3.654\times {10}^{-9}\text{g}/{\text{cm}}^3.\hfill \end{array}$$

In steady state with $P=\overline{P}$, $L=\overline{L}$ and $Q=\overline{Q}$, we have, by Eq (12), $\overline{Q}=\sigma \overline{P}\overline{L}$. We take $K_{TQ}=\frac{1}{2}\overline{Q}=\frac{1}{2}\sigma \overline{P}\overline{L}$. Hence, $Q/K_{TQ}=PL/\left(\frac{1}{2}\overline{P}\overline{L}\right)$ and

$$\begin{array}{c}\hfill \frac{1}{1+Q/K_{TQ}}=\frac{1}{1+PL/\left(\frac{1}{2}\overline{P}\overline{L}\right)}=\frac{1}{1+PL/K_{TQ}^{\prime }},\end{array}$$

where $K_{TQ}^{\prime }:=\frac{1}{2}\overline{P}\overline{L}=\frac{1}{2}\times (7.47\times {10}^{-10})\times (3.654\times {10}^{-9})=1.365\times {10}^{-18}$ g²/cm⁶.

Eq (13): By [42], the half-life of anti-PD-1 is 15 days, so that $d_A=\frac{\text{ln}2}{15}=4.62\times {10}^{-2}$ day⁻¹. We assume that 10% of A is used in blocking PD-1, while the remaining 90% degrades naturally. Hence, in steady state, μ_PAPA/10% = d_AA/90%, so that

$$\begin{array}{c}\hfill {\mu }_{PA}=\frac{d_A}{9P}=\frac{4.62\times {10}^{-2}}{9\times (7.47\times {10}^{-10})}=6.87\times {10}^6{\text{cm}}^3/\text{g}·\text{day}.\end{array}$$

If the percentage of A used in blocking PD-1 is changed, the value of μ_PA will also change, but the results of simulations do not change qualitatively (not shown here).

Sensitivity analysis

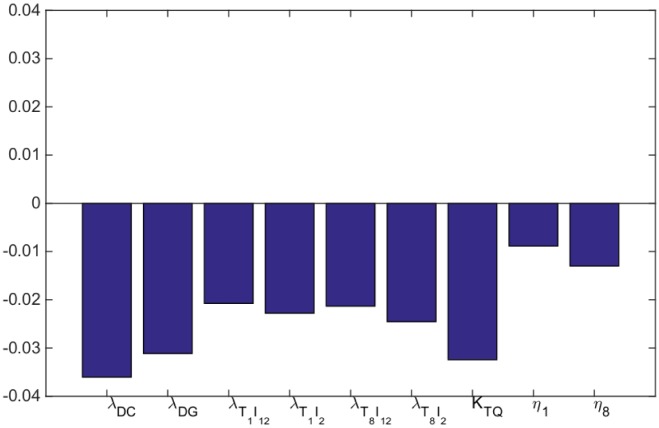
We performed sensitivity analysis, with respect to the tumor radius R at day 60, with respect to some of the production parameters of the System (2)–(13), namely, λ_DC, λ_DG, λ_T1I12, λ_T1I2, λ_T8I12, λ_T8I2, and the important parameters K_TQ, η₁ and η₈. Following the method in [64], we performed Latin hypercube sampling and generated 1000 samples to calculate the partial rank correlation coefficients (PRCC) and the p-values with respect to the tumor radius at day 60. In sampling all the parameters, we took the range of each from 1/2 to twice its values in Tables 2 and 3. The results are shown in Fig 8.

Fig 8. Statistically significant PRCC values (p-value < 0.01) for R(t) at day 60.

Not surprisingly all the parameters are negatively correlated with the tumor radius. We note that the highest negatively correlated parameters are the activation rate of dendritic cells by cancer cells (λ_DC) and the inhibition of T cells activation by PD-1-PD-L1 complex (K_TQ). However, with different values of γ_G and γ_A the parameter λ_DG can exceed λ_DC.

Computational method

We employ moving mesh method [34] to numerically solve the free boundary problem for the tumor proliferation model. To illustrate this method, we take Eq (2) as example and rewrite it as the following form:

$$\begin{array}{c}\hfill \frac{\partial D(r,t)}{\partial t}={\delta }_D\Delta D(r,t)-div\left(\mathbf{u}D\right)+F,\end{array}$$ (24)

where F represents the term in the right hand side of Eq (2). Let $r_i^k$ and $D_i^k$ denote numerical approximations of i-th grid point and $D(r_i^k,n\tau )$, respectively, where τ is the size of time-step. The discretization of Eq (24) is derived by the fully implicit finite difference scheme:

$$\begin{array}{c}\hfill \frac{D_i^{k+1}-D_i^k}{\tau }={\delta }_D(D_{rr}+\frac{2}{r_i^k}{D}_r)-(\frac{2}{r_i^{k+1}}{u}_i^{k+1}+u_r)D_i^{k+1}-u_i^{k+1}{D}_r+F_i^{k+1},\end{array}$$ (25)

where $D_r=\frac{h_{-1}^2{D}_{i+1}^{k+1}-h_1^2{D}_{i-1}^{k+1}-(h_1^2-h_{-1}^2)D_i^{k+1}}{h_1(h_{-1}^2-h_1{h}_{-1})}$, $D_{rr}=2\frac{h_{-1}{D}_{i+1}^{k+1}-h_1{D}_{i-1}^{k+1}+(h_1-h_{-1})D_i^{k+1}}{h_1(h_1{h}_{-1}-h_{-1}^2)}$, $u_r=\frac{h_{-1}^2{u}_{i+1}^{k+1}-h_1^2{u}_{i-1}^{k+1}-(h_1^2-h_{-1}^2)u_i^{k+1}}{h_1(h_{-1}^2-h_1{h}_{-1})}$, $h_{-1}=r_{i-1}^{k+1}-r_i^{k+1}$ and $h_1=r_{i+1}^{k+1}-r_i^{k+1}$. The mesh moves by $r_i^{k+1}=r_i^k+u_i^{k+1}\tau$, where $u_i^{k+1}$ is solved by the velocity equation.

Data Availability

All relevant data are within the paper.

Funding Statement

This work is supported by the Mathematical Biosciences Institute and the National Science Foundation (Grant DMS 0931642), and the Renmin University of China and the International Postdoctoral Exchange Fellowship Program 2016 by the Office of China Postdoctoral Council.