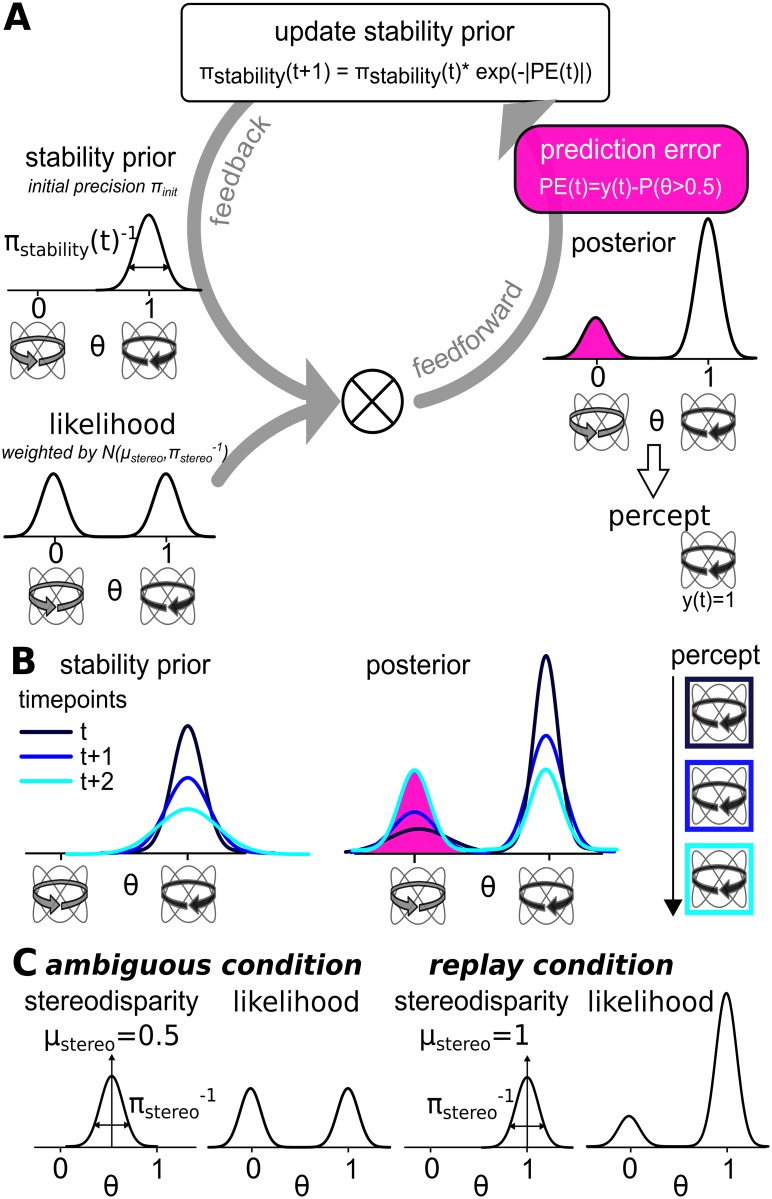
Fig 1. Modelling procedures.

A. In the modelling approach illustrated here, we capture the temporal dynamics of bistable perception by changes in a continuously updated stability prior, which is combined with a bimodal likelihood representing the sensory input (see ‘feedback’ arrow). Under ambiguous viewing conditions, the likelihood contains equivalent evidence for both perceptual interpretations of the bistable stimulus. The mean of the prior ‘perceptual stability’ is defined by μ_stability, which corresponds to the preceding perceptual decision y(t − 1) (here centered around ‘1’ for counter-clockwise rotation of the Lissajous figure). The impact of the prior on the bimodal likelihood is determined by its precision (the inverse of variance) π_stability. If a new perceptual decision was adopted at the preceding overlapping configuration of the Lissajous figure, this precision is set to π_init. Otherwise, π_stability is repeatedly updated by a prediction error signal. This signal results from residual evidence for the alternative explanation of the bistable stimulus and is given by the difference between P(θ > 0.5) and the current perceptual decision y(t) (see ‘feedforward’ arrow). In this example, the prediction error signal stems from remaining evidence for clockwise rotation (centered around ‘0’), as the current perceptual decision represents counter-clockwise rotation (y(t) = 1) of the stimulus. Overtime, the stability prior is weakened, which is accompanied by an increasing probability for a novel transition in perception. B. Here, we depict the temporal evolution of the stability prior (left panel) and the corresponding posterior (right panel) at three successive overlapping configurations of the Lissajous figure (dark to light blue). As the precision of the stabilizing prior is gradually reduced, the posterior relaxes to equivalent probability for both perceptual interpretations of the stimulus. This is accompanied by escalating prediction error signals and increased likelihood for a perceptual transition. C. Furthermore, our approach accounts for additional sensory evidence, which is realized by a stereodisparity signal and used to disambiguate the Lissajous figure in the ‘replay’ condition. To this end, we introduce a ‘stereodisparity’ distribution (characterized by mean μ_stereo and precision π_stereo), which serves as a weight on the bimodal likelihood. In the ambiguous condition (left panel), μ_stereo is centered around 0.5 and is thus uninformative with regard to the two perceptual interpretations of the stimulus. In the replay condition (right panel), μ_stereo is centered around ‘0’ or ‘1’ (depending on the direction of stereodisparity). The strength of the bias in the direction of either percept introduced by the stereodisparity signal scales with the precision π_stereo.