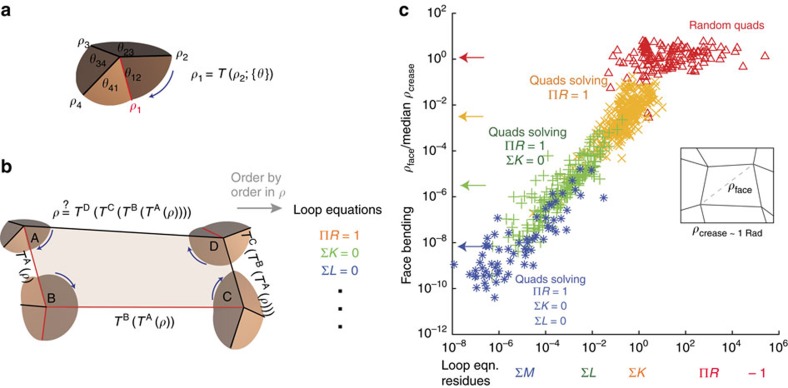
Figure 2. Loop equations uncover folding modes of variable face bending over orders of magnitude.

(a) Folding angles ρ₁, ρ₂ of adjacent creases at a 4-vertex are related by a transfer function T, determined by in-plane angles θ. (b) For a quad to be foldable, a fold angle ρ of an edge must return as ρ when transported around the loop using transfer functions T^A, T^B, T^C, T^D. For a smooth folding motion, the equation must be satisfied order by order in 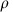. (c) Face bending can be dramatically reduced in a controlled manner by solving loop equations in sequence. Random quads (red triangles), not designed to solve any loop equation, show face bending comparable to crease folding. Quads solving the first loop equation ΠR=1 (orange × s) typically have face bending <10⁻² Rad. We find that the residue of the highest loop equation not solved determines the extent of face bending; hence orange points and green points show the drop of face bending with decreasing ∑K and ∑L respectively.