IMPROVED Cr II log(gf ) VALUES AND ABUNDANCE DETERMINATIONS IN THE PHOTOSPHERES OF THE SUN AND METAL-POOR STAR HD 84937

Abstract

New emission branching fraction (BF) measurements for 183 lines of the second spectrum of chromium (Cr II) and new radiative lifetime measurements from laser-induced fluorescence for 8 levels of Cr⁺ are reported. The goals of this study are to improve transition probability measurements in Cr II and reconcile solar and stellar Cr abundance values based on Cr I and Cr II lines. Eighteen spectra from three Fourier Transform Spectrometers supplemented with ultraviolet spectra from a high-resolution echelle spectrometer are used in the BF measurements. Radiative lifetimes from this study and earlier publications are used to convert the BFs into absolute transition probabilities. These new laboratory data are applied to determine the Cr abundance log ε in the Sun and metal-poor star HD 84937. The mean result in the Sun is 〈logε (Cr II)〉 = 5.624±0.009 compared to 〈logε(Cr I)〉 = 5.644 ± 0.006 on a scale with the hydrogen abundance log ε(H) = 12 and with the uncertainty representing only line-to-line scatter. A Saha (ionization balance) test on the photosphere of HD 84937 is also performed, yielding 〈logε(Cr II)〉 = 3.417 ± 0.006 and 〈log ε(Cr I, lower level excitation potential E. P. >30 eV)〉 = 3.3743±30.011 for this dwarf star. We find a correlation of Cr with the iron-peak element Ti, suggesting an associated nucleosynthetic production. Four iron-peak elements (Cr along with Ti, V, and Sc) appear to have a similar (or correlated) production history—other iron-peak elements appear not to be associated with Cr.

1. INTRODUCTION

Iron- (Fe-)peak elements are known to be produced in core-collapse supernovae (SNe). “Old” metal-poor (MP) stars reveal very different relative Fe-peak abundance patterns from early SNe. SNe Ia, which became more common as the Galaxy aged, explain only part of the abundance pattern evolution. Variations in the relative average Fe-peak abundance values can be ± 1 dex for metallicities ranging from solar ([Fe/H]≡0) to −4 (e.g., Figure 12 of McWilliam 1997).⁶ Henry et al. (2010) more recently reviewed Fe-peak abundances as a function of metallicity.

It is not surprising that relative Fe-peak abundance patterns are different from early stars because such stars were likely very massive, perhaps rapidly rotating, and started with (near-) zero metallicity. Observations of gamma-ray bursts are yielding clues on early nucleosynthesis as are studies of abundance patterns in MP stars. The study of Fe-peak abundance patterns in MP stars is to some extent hindered by the possible breakdown of traditional one-dimensional/local thermal equilibrium (1D/LTE) photospheric models. Asplund (2005) discusses the need for three-dimensional/non-LTE (3D/NLTE) models, but such models are still hindered by the lack of reliable cross-sections and rate constants for inelastic and super-elastic collisions of H and He atoms with metal atoms and atomic ions. Theoretical rate constants are being improved, especially by Barklem and collaborators (Barklem et al. 2005, 2011; Barklem 2016). Reliable rate constants for ion pair “mutual neutralization” reactions involving H⁻ + a metal ion or the time-reversed “ion pair production” involving neutral excited metal atoms +H are also critically needed. The cryogenic electrostatic storage ring DESIREE at Stockholm University will make it possible to measure many needed charge transfer cross-sections and rates (Schmidt et al. 2013).

The long-term objective of our collaboration is to map the relative abundances of Fe-peak elements at low metallicity. We are systematically improving and expanding lab data for Fe-peak atoms and ions using radiative lifetime measurements from laser-induced fluorescence (LIF) and emission branching fraction (BF) data from high-resolution spectrometers. We started with Cr I (Sobeck et al. 2007) and then worked on Mn I and Mn II (Den Hartog et al. 2011). Difficulties in measuring weak branches due to multiplex noise in Fourier Transform Spectrometer (FTS) data were part of the motivation for developing a high-resolution, 3 m focal length echelle spectrometer with broad spectral coverage and excellent UV sensitivity (Wood & Lawler 2012). Various combinations of FTS data and 3 m echelle data led to rapid progress on Ti I (Lawler et al. 2013), Ti II (Wood et al. 2013), V II (Wood et al. 2014a), Ni I (Wood et al. 2014b), V I (Lawler et al. 2014), Fe I (Den Hartog et al. 2014b; Ruffoni et al. 2014), and Co I (Lawler et al. 2015). Sobeck et al. (2007) noted difficulties in reconciling abundance values from lines of Cr I to abundance values from lines of Cr II in the Sun and in metal-poor stars. The relatively new log(gf ) values for abundance measurements using lines of Cr II are primarily from Nilsson et al. (2006). Nilsson et al. used the modern method of normalizing emission BFs from FTS spectra with radiative lifetimes from LIF measurements. Sobeck et al. discussed the challenge of BF measurements in Cr II due to the large variation of intensities and wavelengths of branches from a common upper level. Scott et al. (2015, p. 8) commented that “the small number of gf-values available from Nilsson et al. for good solar lines also return abundances that are highly inconsistent with each other.” The above difficulties and comments provide motivation to remeasure some of the radiative lifetimes and BFs of Cr II and to expand the measurements by Nilsson et al. This paper reports new radiative lifetime measurements for eight levels and BF measurements for 183 lines of Cr II. All 8 lifetimes and 102 of the BFs overlap with Nilsson et al. Our initial application of these Fe-peak data is the determination of improved elemental abundances in the Sun and metal-poor turn-off star HD 84937.

2. RADIATIVE LIFETIME MEASUREMENTS FOR Cr II

Most of the radiative lifetimes used by Nilsson et al. (2006) to normalize their BF measurements are from Schade et al. (1990). The radiative lifetime measurements from Schade et al. are thought to be highly reliable LIF measurements using an organic dye laser with a short pulse duration of 200 ps. The shortest lifetimes measured by Schade et al. (1990) have been checked using multiple LIF experiments. Eight new lifetime measurements on levels of ionized Cr above 50,000 cm⁻¹ excitation energy values were reported by Nilsson et al. (2006). We selected these levels to remeasure using time-resolved LIF on a slow beam of Cr ions. The time-resolved LIF experiment at the University of Wisconsin (UW) has been used on many atoms and ions since it was built in 1980. Rather than give another detailed description, we refer the interested reader to recent work on radiative lifetimes of neutral and ionized vanadium by Den Hartog et al. (2014a). The most important technique used to ensure the accuracy of lifetime measurements from the UW LIF experiment is the regular remeasurement of selected benchmark lifetimes. These benchmark lifetimes are from very accurate theory with uncertainties ≤1%, or from other measurements made with a different technique characterized by different systematic effects and generally smaller total uncertainty. The 3.85 ns radiative lifetime of the 3²P_3/2 level of singly ionized Mg (National Institute of Standards and Technology (NIST) critical compilation of Kelleher & Podobedova 2008; uncertainty of ≤1% at 90% confidence level) is clearly the best benchmark for lifetime measurements around 4 ns, and it is employed here for our Cr II remeasurements. The comparison shown in Table 1 strongly supports the eight lifetime measurements by Nilsson et al. (2006). The level of agreement in Table 1 is actually not unusual for LIF measurements of radiative lifetimes. It is the BF measurements, especially those spanning large wavelength and intensity ranges, that are the primary challenge. The new lifetime results in Table 1 as well as the lifetime results from Schade et al. (1990) are used to put the absolute scale on the transition probabilities in this work on Cr II.

Table 1.

New Radiative Lifetime Measurements on the 3d⁴(⁵D)4p z⁴F and z⁴D Levels Studied Previously by Nilsson et al. (2006) at Lund

Term and J	Level	Radiative Lifetime
	(cm−1)	Lund (ns)	This Expt. (±5%) (ns)
z4F3/2	51584.100	4.2(4)	4.2
z4F5/2	51669.406	4.1(4)	4.3
z4F7/2	51788.815	4.1(3)	4.3
z4F9/2	51942.664	4.1(3)	4.2
z4D1/2	54417.955	4.3(4)	4.2
z4D3/2	54499.491	4.3(4)	4.2
z4D5/2	54625.595	4.3(4)	4.2
z4D7/2	54784.450	4.3(4)	4.2

Note. The ±5% uncertainty of this LIF experiment is a conservative estimate of the possible systematic error, and it is larger than the statistical uncertainty of each lifetime.

3. BF MEASUREMENTS FOR Cr II

The challenge of BF measurements in Cr II is largely in measuring BFs for weak branches with large wavelength separation from the dominant branches of the common upper level. The large wavelength separation requires great care in establishing a reliable relative radiometric calibration. A range of hollow cathode discharge (HCD) lamp currents is essential to test for possible optical depth error. Optical depth has little effect on the dominant BFs but artificially enhances weak BFs. The sum of all BFs from an upper level is unity by definition and thus the weakest branches inherit most of the uncertainty from relative measurements. The weak branches in Cr II are prone to error from blending with buffer gas and Cr I and Cr II lines. The preferred technique for separating a blend with a buffer gas line is to switch from Ar to Ne buffer gas or Ne to Ar. A good technique for separating a blend of a Cr II line with a line of Cr I is based on the current dependence in the ratio of a line pair from a common upper level (e.g., Lawler et al. 2011). First and second spectra lines from HCD lamps generally have rather different current dependences. A current dependence can also indicate an optical depth problem if one of the lines in a pair is a dominant branch. Blends of a pair of Cr II lines are often difficult to separate since both may have a similar current dependence. The recent experimental improvement of both Cr I and Cr II energy level values⁷ (Saloman 2012; Sansonetti & Nave 2014; Kramida et al. 2015) enables another blend separation technique on FTS data that can work both for blends of Cr II and Cr I lines as well as pairs of Cr II lines (e.g., Lawler et al. 2015). The internal wave number accuracy and precision of FTS data is better than 1 part in 10⁷. The comparison of a center-of-gravity (cog) wave number of a possibly blended feature to Ritz wave numbers for the possibly blended lines is a simple way to identify and/or separate a blended feature. This separation technique works best with a signal-to-noise ratio (S/N) ⩾ 10 and a Ritz wave number separation ⩾0.05 cm⁻¹. Other advantages of FTS instruments including the broad coverage, high spectral resolving power, and large etendue are well known. Table 2 lists the 18 FTS spectra used in this work on Cr II. The first 10 of the FTS spectra are from the National Solar Observatory (NSO) 1 m FTS (Brault 1976) and are in the public domain.⁸ These are the same spectra used by Sobeck et al. (2007) for BF measurements on Cr I. Data from two instruments at the NIST, the VUV Chelsea Instruments FT700 and the 2 m optical FTS, are also included and will be available online in the near future. These data were supplemented with data from the UW 3 m focal length echelle spectrometer at high wave numbers. The echelle spectra are listed in Table 3.

Table 2.

Fourier Transform Spectra of Custom Water-cooled Hollow Cathode Discharge (HCD) and a Penning Discharge (Index 17) Lamp

Index #	Year, Day	Serial #	FTS	Buffer Gas and Pressure (mmHg)	Lamp Cur- rent (mA)	Wave Number Range (cm−1)	Limit of Resolution (cm−1)	Coadds	Beam Splitter	Filter and Detectora	Relative Radiometric Calibration
1	1982 Jun 25	7	NSO 1 m FTS	Ar 0.65	500	7664–44591	0.057	8	UV	CS9-54 filter and Mid Range Si PD	Ar II lines
2	1982 Jun 26	4	NSO 1 m FTS	Ar 1.0	100	7664–44591	0.057	6	UV	CS9-54 filter and Mid Range Si PD	Ar II lines
3	1984 Jul 26	6	NSO 1 m FTS	Ne 3.0	750	7982–45407	0.054	4	UV	NSF and R166 PMT, WG295 filter and Mid Range Si PD	W-filament, piece- wise flat in UV
4	1984 Jul 26	7	NSO 1 m FTS	Ne 3.3	1500	7982–45407	0.054	4	UV	NSF and R166 PMT, WG295 filter and Mid Range Si PD	W-filament, piece- wise flat in UV
5	1984 Jul 26	8	NSO 1 m FTS	Ne 3.3	1500	7982–45407	0.054	4	UV	NSF and R166 PMT, WG295 filter and Mid Range Si PD	W-filament, piece- wise flat in UV
6	1980 Feb 28	1	NSO 1 m FTS	Ar 2.5	500	7908–28921	0.035	4	Vis	GG375 filter and SB Si PD	Ar II lines
7	1980 Mar 25	3	NSO 1 m FTS	Ne 4.0	950	13489–27089	0.034	10	Vis	GG400 + CS4-96 filters and SB Si PD	W-filament
8	1982 Jun 25	6	NSO 1 m FTS	Ne 2.0	500	7664–44591	0.057	9	UV	CS9-54 filter and Mid Range Si PD	piecewise flat
9	1982 Jun 25	8	NSO 1 m FTS	Ne 1.2	500	7664–44591	0.057	8	UV	CS9-54 filter and Mid Range Si PD	piecewise flat
10	1984	11	NSO	Ne 2.6	500	7982–45407	0.054	8	UV	NSF and R166 PMT,	piecewise flat
	Jul 26		1 m FTS							WG295 and Mid Range Si PD
11	2000 Nov 6	1	NIST FT700	Ar 0.65	1500	22000–44000	0.033	64	CaF2	UG11 1 mm filter and R106UH PMT (350s cathode)	Ar II lines
12	2000 Nov 6	2	NIST FT700	Ar 0.65	200	22000–44000	0.033	64	CaF2	UG11 1 mm filter and R106UH PMT (350s cathode)	Ar II lines
13	2000 Nov 16	1	NIST FT700	Ar 0.66	1500	19000–38000	0.027	64	CaF2	BG4 filter and R106UH PMT (350s cathode)	W-filament
14	2000 Nov 15	2	NIST FT700	Ar 0.66	700	19000–38000	0.030	32	CaF2	BG4 filter and R106UH PMT (350s cathode)	W-filament
15	2000 Nov 15	1	NIST FT700	Ar 0.65	200	19000–38000	0.030	32	CaF2	BG4 filter and R106UH PMT (350s cathode)	W-filament
16	2000 Oct 26	1	NIST FT700	Ne 0.5	700	28000–56000	0.050	64	CaF2	NSF and R7154 PMT (250s cathode)	piecewise flat
17	2000 Dec 8	1	NIST FT700	Ne 0.003	1400	28000–56000	0.150	128	CaF2	NSF and R7154 PMT (250s cathode)	piecewise flat
18	2011 Jun 10	7	NIST 2 m FTS	Ne 3.0	2000	0–35000	0.020	107	FS	NSF and Large area Si PD	W-filament

Notes. Spectra were recorded using the 1 m FTS on the McMath telescope at the NSO, Kitt Peak, AZ, and the VUV Chelsea Instruments FT700 and the 2 m Optical FTS at NIST, Gaithersburg, MD.

^aDetector types include the Super Blue (SB) Si photodiode (PD), Mid Range Si PD, and R166 photomultiplier (PMT) at NSO. Detector types at NIST include R106UH PMT, R7154 PMT, and Large area Si PD. The UV beam splitter at NSO is fused silica (FS). Filter numbers (Schott and Corning) are listed and NSF means No Spectral Filter. There are two output ports on an FTS and occasionally two different detector/filter combinations are used for a single spectrum.

Table 3.

Echelle Spectra of Custom Water-cooled HCD Lamp

Index	Date	Serial Numbersa	Buffer Gas and Pressure	Lamp Current	Wavelength Range	Resolving Power	Coadds	Exposure Time	Relative Radiometric Calibration
51–55	2016 Feb 25	1, 3, 5, 7, 9	Ne 7.0 mmHg	100 mA	2100–3200 Å	250,000	714	0.18 s	D2 lamp checked against AMA
56–60	2016 Mar 11	1, 3, 5, 7, 9	Ne 7.5 mmHg	20 mA	2100–3200 Å	250,000	231	2.6 s	D2 lamp checked against AMA

Note.

^aAt least three CCD frames are needed to capture a complete echelle grating order in the UV. In the above data, five CCD frames are used to provide redundancy and a check for lamp drift.

The relative radiometric calibration of each spectrum is listed in the last column. The use of selected Ar II lines for a relative radiometric calibration is our standard method. This method was established and checked by Adams & Whaling (1981), Danzmann & Kock (1982), Hashiguchi & Hasikuni (1985), and Whaling et al. (1993). It incorporates any effects from loss of lamp window transmittance and/or reflection from the back of the hollow cathode. This method is best established below 35,000 cm⁻¹, and it is supplemented with 3 m echelle data of Table 3 for work on Cr II. Some of the Cr/Ne data in Table 1 are calibrated using W-filament spectra. Such standard lamp FTS spectra, when the interferogram center burst is isolated and transformed, are useful for wave numbers above 25,000 cm⁻¹ for overlap with D2 standard lamp spectra. Other Cr/Ne data are listed as having a “piecewise flat” calibration. Such data with high S/N can be used to improve BFs inside a Cr II multiplet that covers a small spectral range.

During analysis of the spectra listed in Tables 2 and 3, our standard method of looking for all possible transitions between known energy levels of ionized Cr that satisfy the parity change and |ΔJ| ≤ 1selection rules is used. Of course, the analysis is checked against the line list of Sansonetti & Nave (2014) to verify line classifications.

The UV extension above 35,000 cm⁻¹ as well as a final check for optical depth is made using the spectra of Table 3 from the 3 m echelle. The heavily used D2 lamp listed in Table 3 is periodically checked with a second, little used, NIST-traceable D₂ lamp, and against a windowless Ar MiniArc (AMA; Bridges & Ott 1977) calibrated personally by Dr. Bridges at NIST.

The FTS spectrum with Index #18 in Table 2 is unique. It was recorded at NIST during 2011 as part of the effort to improve energy level values of Cr II, which culminated in the Sansonetti & Nave (2014) paper. It is the only optical spectrum listed in the Sansonetti & Nave paper, and it was recorded during the conditioning of a newly assembled HCD lamp. The S/N of the optical lines of Cr II in Spectrum #18 is vastly superior to all other FTS data in Table 2. The presence of Balmer lines in this spectrum suggests that the lamp was still slightly contaminated with water vapor while Spectrum #18 was recorded. Efforts to reproduce Spectrum #18 have not been successful. Although these data enabled us to measure BFs appreciably smaller than 0.01 for optical lines of Cr II, essentially all of our results for wave numbers below 20,000 cm⁻¹ are from this single spectrum. Lines from a single spectrum were typically suppressed in past publications from our collaboration, but kept in the BF normalization. We have included the Cr II optical lines from Spectrum #18 in our results because the optical lines are important to ground-based astronomy. The water vapor in Spectrum #18 likely affected electron emission and sputtering at the cathode but cannot affect measured gfvalues between well-defined (narrow) levels of ionized Cr.

Although a correction is sometimes made for “residuals” or unobserved lines in BF studies, no correction is applied to our BF measurements. The spectra listed in Tables 2 and 3, especially Spectrum #18 of Table 2, enabled us to measure BFs appreciably <0.01. Contributions of possible infrared (IR) branches beyond the wave number limit of the listed spectra can be neglected because of the short, <6 ns, lifetimes of the ionized Cr levels of interest. The transition strength S, proportional to the transition electric dipole moment squared, of a dominant UV branch from an upper level of interest is large. An Einstein A coefficient of a possible residual IR line, and thus the BF of that line, scales as the product of the S of the IR line and its wave number cubed. All lines in the ≈40,000 to ≈10,000 cm⁻¹ range from upper levels of interest are measured in this study. Even if the S of a residual IR line was large, the BF would be suppressed by a factor of ≤1/64 compared to the dominant UV BF(s) near 40,000 cm⁻¹ and thus negligible.

The BFs and transition probabilities of lines from the 3d⁴ (⁵D) 4p z⁶P^o levels near 48,500 cm⁻¹ are not included in this study. The dominant multiplet from the z⁶P^o term near 206 nm has a large separation from the multiplet near 275 nm. These BFs and transition probabilities were measured initially with radiative lifetime normalization from LIF measurements by Bergeson & Lawler (1993), remeasured (e.g., Nilsson et al. 2006), and computed in theoretical studies (e.g., Aashamar & Luke 1994). Improved measurements are possible using our 3 m echelle with a lower dispersion prism (e.g., CaF₂) as an order separator so that both multiplets are observable with a single prism setting. Remeasurement with the existing fused silica order separating prism in the 3 m echelle would not yield improved results for lines from the z⁶P^o term because lines of the 206 nm multiplet and the 275 nm multiplet cannot be recorded on a single CCD frame.

As in our earlier papers, uncertainties on final mean BFs are evaluated from the strength of the BFs, the S/N of the spectral lines, and the wave number difference of lines from the common upper level. The conservative estimate of the calibration uncertainty is 0.001%/cm⁻¹ of the difference between a line and the dominant branch(es) from the common upper level (Wickliffe et al. 2000). Of course, this calibration uncertainty results in uncertainties of about 20% on BFs of the optical lines of Cr II because of the large wave number difference from the dominant UV lines from the upper levels of interest.

4. TRANSITION PROBABILITIES FOR LINES OF Cr II AND COMPARISONS

The 18 FTS spectra of Table 2 in combination with the 3 m echelle spectra of Table 3 yielded BFs for 183 lines. As mentioned above, these BFs are combined with radiative lifetimes from LIF measurements by Schade et al. (1990) and with new lifetime measurements for eight levels. The eight new lifetimes agreed very well with earlier measurements by Nilsson et al. (2006). The BF and radiative lifetime fractional uncertainties are combined in quadrature. Radiative lifetime uncertainties tend to dominate final transition probability uncertainties for strong lines of, or near, the dominant branch (es), but in most cases BF uncertainties dominate. Table 4 is a list of the final transition probabilities and uncertainties.

Table 4.

Experimental Atomic Transition Probabilities for 183 Lines of Cr II Organized by Increasing Wavelength in Air

Wavelength in Aira	Upper Level		Lower Level		Transition Probability	log(gf )
(nm)	Valueb (cm−1)	J	Valueb (cm−1)	J	(106 s−1)
253.4336	51942.664	4.5	12496.457	4.5	2.78 ± 0.27	−1.57
265.3581	49706.261	2.5	12032.545	1.5	32.9 ± 1.3	−0.68
265.8588	49564.504	1.5	11961.746	0.5	56.7 ± 1.8	−0.62
266.1722	49706.261	2.5	12147.771	2.5	9.9 ± 0.4	−1.20
266.3419	49838.380	4.5	12303.820	3.5	51. ± 3.	−0.26
266.3604	49564.504	1.5	12032.545	1.5	0.60 ± 0.10	−2.59
266.3674	49492.711	0.5	11961.746	0.5	40. ± 4.	−1.07
266.6014	49645.806	3.5	12147.771	2.5	98. ± 3.	−0.08
266.8709	49492.711	0.5	12032.545	1.5	131. ± 8.	−0.55
267.1807	49564.504	1.5	12147.771	2.5	98. ± 3.	−0.38
267.2828	49706.261	2.5	12303.820	3.5	49.2 ± 2.0	−0.50
267.7155	49645.806	3.5	12303.820	3.5	104. ± 3.	−0.05
267.7160	49838.380	4.5	12496.457	4.5	209. ± 11.	0.35
267.8791	49351.734	2.5	12032.545	1.5	67. ± 3.	−0.36
268.7088	49351.734	2.5	12147.771	2.5	37.3 ± 1.8	−0.62
269.1038	49645.806	3.5	12496.457	4.5	59.7 ± 2.4	−0.28
269.8407	49351.734	2.5	12303.820	3.5	38.5 ± 2.0	−0.60
269.8685	49005.847	1.5	11961.746	0.5	52. ± 4.	−0.65
270.3852	49005.847	1.5	12032.545	1.5	7.8 ± 0.7	−1.46
271.2306	49005.847	1.5	12147.771	2.5	32.1 ± 2.6	−0.85
271.7507	48749.278	0.5	11961.746	0.5	16.5 ± 1.4	−1.44
272.2747	48749.278	0.5	12032.545	1.5	51. ± 4.	−0.95
283.5632	47751.600	5.5	12496.457	4.5	250. ± 6.	0.56
284.3246	47464.557	4.5	12303.820	3.5	192. ± 5.	0.37
284.9835	47227.219	3.5	12147.771	2.5	152. ± 4.	0.17
285.5673	47040.276	2.5	12032.545	1.5	113. ± 3.	−0.08
285.6762	54625.595	2.5	19631.206	1.5	34.6 ± 1.8	−0.59
285.7399	54784.450	3.5	19797.859	2.5	20.8 ± 1.2	−0.69
285.8651	54499.491	1.5	19528.229	0.5	37.6 ± 2.0	−0.73
285.8910	47464.557	4.5	12496.457	4.5	46.4 ± 1.9	−0.25
286.0931	46905.137	1.5	11961.746	0.5	75.1 ± 2.2	−0.43
286.2569	47227.219	3.5	12303.820	3.5	86.8 ± 2.5	−0.07
286.5104	47040.276	2.5	12147.771	2.5	111. ± 3.	−0.08
286.5332	54417.955	0.5	19528.229	0.5	79. ± 4.	−0.71
286.6740	46905.137	1.5	12032.545	1.5	136. ± 3.	−0.17
286.7094	54499.491	1.5	19631.206	1.5	64. ± 3.	−0.50
286.7647	46823.306	0.5	11961.746	0.5	176. ± 4.	−0.36
287.0432	54625.595	2.5	19797.859	2.5	93. ± 5.	−0.16
287.3483	46823.306	0.5	12032.545	1.5	56.7 ± 2.1	−0.85
287.3814	54417.955	0.5	19631.206	1.5	82. ± 4.	−0.69
287.5990	54784.450	3.5	20024.012	3.5	133. ± 7.	0.12
287.6244	46905.137	1.5	12147.771	2.5	27.3 ± 1.2	−0.87
287.7976	47040.276	2.5	12303.820	3.5	13.6 ± 0.6	−0.99
287.8447	47227.219	3.5	12496.457	4.5	5.4 ± 0.5	−1.27
288.0864	54499.491	1.5	19797.859	2.5	60. ± 3.	−0.52
288.9194	54625.595	2.5	20024.012	3.5	33.3 ± 1.9	−0.60
303.2919	54784.450	3.5	21822.504	2.5	6.8 ± 0.5	−1.13
304.7607	54625.595	2.5	21822.504	2.5	6.3 ± 0.4	−1.28
304.7759	54625.595	2.5	21824.141	1.5	4.91 ± 0.30	−1.39
305.9368	54499.491	1.5	21822.504	2.5	2.19 ± 0.18	−1.91
305.9482	54499.491	1.5	21823.720	0.5	3.35 ± 0.29	−1.73
305.9522	54499.491	1.5	21824.141	1.5	7.8 ± 0.5	−1.36
306.7136	54417.955	0.5	21823.720	0.5	10.2 ± 0.6	−1.54
306.7175	54417.955	0.5	21824.141	1.5	4.4 ± 0.5	−1.91
311.8649	51584.100	1.5	19528.229	0.5	141. ± 7.	−0.08
312.0369	51669.406	2.5	19631.206	1.5	143. ± 7.	0.10
312.4978	51788.815	3.5	19797.859	2.5	156. ± 8.	0.26
312.8700	51584.100	1.5	19631.206	1.5	50.4 ± 2.9	−0.53
313.2057	51942.664	4.5	20024.012	3.5	182. ± 9.	0.43
313.6686	51669.406	2.5	19797.859	2.5	40.6 ± 2.5	−0.44
314.5104	51584.100	1.5	19797.859	2.5	2.97 ± 0.21	−1.75
314.7227	51788.815	3.5	20024.012	3.5	24.8 ± 1.7	−0.53
315.9103	51669.406	2.5	20024.012	3.5	1.38 ± 0.08	−1.91
318.0696	51942.664	4.5	20512.096	5.5	43. ± 3.	−0.19
318.1422	51942.664	4.5	20519.269	4.5	2.99 ± 0.24	−1.34
319.6925	51788.815	3.5	20517.792	3.5	5.3 ± 0.4	−1.19
319.7076	51788.815	3.5	20519.269	4.5	39.2 ± 3.0	−0.32
320.8589	51669.406	2.5	20512.063	2.5	4.83 ± 0.27	−1.35
320.9179	51669.406	2.5	20517.792	3.5	36. ± 3.	−0.48
321.7399	51584.100	1.5	20512.063	2.5	38.2 ± 2.9	−0.62
332.4058	49706.261	2.5	19631.206	1.5	3.6 ± 0.3	−1.44
332.8350	49564.504	1.5	19528.229	0.5	4.5 ± 0.4	−1.53
333.6121	51788.815	3.5	21822.504	2.5	0.26 ± 0.04	−2.47
333.6325	49492.711	0.5	19528.229	0.5	28.3 ± 2.0	−1.02
333.9801	49564.504	1.5	19631.206	1.5	22.9 ± 1.8	−0.81
334.2581	49706.261	2.5	19797.859	2.5	20.0 ± 1.6	−0.70
334.7831	49492.711	0.5	19631.206	1.5	27.6 ± 1.9	−1.03
334.9352	49645.806	3.5	19797.859	2.5	0.96 ± 0.10	−1.89
335.3124	49838.380	4.5	20024.012	3.5	2.29 ± 0.22	−1.41
335.8500	49564.504	1.5	19797.859	2.5	47. ± 3.	−0.50
336.0291	54784.450	3.5	25033.668	3.5	47. ± 4.	−0.20
336.1765	54784.450	3.5	25046.714	2.5	8.2 ± 0.6	−0.95
336.3711	49351.734	2.5	19631.206	1.5	0.90 ± 0.08	−2.04
336.8049	49706.261	2.5	20024.012	3.5	89. ± 5.	−0.04
337.8330	54625.595	2.5	25033.668	3.5	10.3 ± 0.8	−0.98
337.9368	54625.595	2.5	25042.760	1.5	11.5 ± 0.9	−0.93
337.9820	54625.595	2.5	25046.714	2.5	25.7 ± 1.9	−0.58
338.2680	49351.734	2.5	19797.859	2.5	13.7 ± 1.2	−0.85
339.1431	49005.847	1.5	19528.229	0.5	5.7 ± 0.3	−1.40
339.2982	54499.491	1.5	25035.344	0.5	11.4 ± 0.9	−1.10
339.3836	54499.491	1.5	25042.760	1.5	16.5 ± 1.3	−0.94
339.4291	54499.491	1.5	25046.714	2.5	17.1 ± 1.4	−0.93
340.2397	54417.955	0.5	25035.344	0.5	21.5 ± 1.8	−1.13
340.3256	54417.955	0.5	25042.760	1.5	23.1 ± 1.7	−1.10
340.3320	49005.847	1.5	19631.206	1.5	36.0 ± 1.8	−0.60
340.8765	49351.734	2.5	20024.012	3.5	51. ± 4.	−0.27
340.8932	49838.380	4.5	20512.096	5.5	0.42 ± 0.06	−2.14
342.1210	48749.278	0.5	19528.229	0.5	61.8 ± 2.9	−0.66
342.2739	49005.847	1.5	19797.859	2.5	66. ± 3.	−0.33
343.3309	48749.278	0.5	19631.206	1.5	58.5 ± 2.7	−0.68
358.5294	49706.261	2.5	21822.504	2.5	11.4 ± 1.1	−0.88
358.5505	49706.261	2.5	21824.141	1.5	4.7 ± 0.5	−1.26
360.3615	49564.504	1.5	21822.504	2.5	3.2 ± 0.3	−1.60
360.3773	49564.504	1.5	21823.720	0.5	4.0 ± 0.4	−1.51
360.3827	49564.504	1.5	21824.141	1.5	1.52 ± 0.17	−1.93
361.3124	49492.711	0.5	21823.720	0.5	0.92 ± 0.09	−2.44
361.3179	49492.711	0.5	21824.141	1.5	4.6 ± 0.3	−1.74
363.1468	49351.734	2.5	21822.504	2.5	6.4 ± 0.7	−1.12
363.1683	49351.734	2.5	21824.141	1.5	2.1 ± 0.3	−1.60
367.7676	49005.847	1.5	21822.504	2.5	4.48 ± 0.29	−1.44
367.7841	49005.847	1.5	21823.720	0.5	5.2 ± 0.3	−1.37
367.7898	49005.847	1.5	21824.141	1.5	2.09 ± 0.13	−1.77
371.2887	48749.278	0.5	21823.720	0.5	1.89 ± 0.15	−2.11
371.2945	48749.278	0.5	21824.141	1.5	9.8 ± 0.6	−1.39
371.5172	51942.664	4.5	25033.668	3.5	1.52 ± 0.13	−1.50
373.8359	51788.815	3.5	25046.714	2.5	1.22 ± 0.09	−1.69
375.4569	51669.406	2.5	25042.760	1.5	0.92 ± 0.08	−1.93
376.5585	51584.100	1.5	25035.344	0.5	0.67 ± 0.07	−2.24
376.6637	51584.100	1.5	25042.760	1.5	0.122 ± 0.022	−2.98
376.7198	51584.100	1.5	25046.714	2.5	0.20 ± 0.04	−2.76
405.1936	49706.261	2.5	25033.668	3.5	0.35 ± 0.05	−2.29
405.4080	49706.261	2.5	25046.714	2.5	0.188 ± 0.028	−2.56
407.2556	54499.491	1.5	29951.816	0.5	0.27 ± 0.05	−2.56
408.6128	54417.955	0.5	29951.816	0.5	1.06 ± 0.17	−2.27
411.0982	54625.595	2.5	30307.367	1.5	0.42 ± 0.09	−2.19
411.3216	49351.734	2.5	25046.714	2.5	0.091 ± 0.018	−2.86
413.2411	54499.491	1.5	30307.367	1.5	0.32 ± 0.05	−2.48
417.1909	49005.847	1.5	25042.760	1.5	0.113 ± 0.024	−2.93
417.9421	54784.450	3.5	30864.433	2.5	0.66 ± 0.09	−1.86
420.7363	54625.595	2.5	30864.433	2.5	0.18 ± 0.04	−2.54
421.5743	48749.278	0.5	25035.344	0.5	0.22 ± 0.03	−2.93
423.3248	54784.450	3.5	31168.575	3.5	0.44 ± 0.06	−2.02
424.2366	54784.450	3.5	31219.332	4.5	3.0 ± 0.4	−1.19
425.2625	54625.595	2.5	31117.325	2.5	0.78 ± 0.12	−1.90
426.1917	54625.595	2.5	31168.575	3.5	2.18 ± 0.29	−1.45
426.9272	54499.491	1.5	31082.884	1.5	0.76 ± 0.13	−2.08
427.5561	54499.491	1.5	31117.325	2.5	2.5 ± 0.3	−1.57
428.4190	54417.955	0.5	31082.884	1.5	3.1 ± 0.4	−1.77
453.9590	54625.595	2.5	32603.349	2.5	0.33 ± 0.06	−2.21
455.4989	54784.450	3.5	32836.653	3.5	2.2 ± 0.3	−1.27
455.8644	54784.450	3.5	32854.250	4.5	14.9 ± 2.0	−0.43
456.5735	54499.491	1.5	32603.349	2.5	1.13 ± 0.17	−1.85
458.8198	54625.595	2.5	32836.653	3.5	11.9 ± 1.6	−0.65
458.9895	54625.595	2.5	32844.707	1.5	0.18 ± 0.04	−2.47
459.2053	54625.595	2.5	32854.940	2.5	2.7 ± 0.4	−1.30
461.6624	54499.491	1.5	32844.707	1.5	3.0 ± 0.4	−1.42
461.8807	54499.491	1.5	32854.940	2.5	10.0 ± 1.4	−0.89
463.4073	54417.955	0.5	32844.707	1.5	13.9 ± 1.9	−1.05
481.2344	51942.664	4.5	31168.575	3.5	0.31 ± 0.04	−1.96
482.4131	51942.664	4.5	31219.332	4.5	3.5 ± 0.4	−0.92
483.6230	51788.815	3.5	31117.325	2.5	0.48 ± 0.06	−1.87
484.8250	51788.815	3.5	31168.575	3.5	2.8 ± 0.4	−1.11
485.6191	51669.406	2.5	31082.884	1.5	0.44 ± 0.06	−2.03
486.0213	51788.815	3.5	31219.332	4.5	0.32 ± 0.04	−2.04
486.4329	51669.406	2.5	31117.325	2.5	2.17 ± 0.28	−1.34
487.6397	51584.100	1.5	31082.884	1.5	2.13 ± 0.28	−1.52
487.6489	51669.406	2.5	31168.575	3.5	0.53 ± 0.08	−1.94
488.4604	51584.100	1.5	31117.325	2.5	0.48 ± 0.07	−2.16
489.1495	51788.815	3.5	31350.874	2.5	0.056 ± 0.010	−2.79
515.3498	49706.261	2.5	30307.367	1.5	0.19 ± 0.04	−2.34
523.2498	51942.664	4.5	32836.653	3.5	0.161 ± 0.027	−2.18
523.7322	51942.664	4.5	32854.250	4.5	1.65 ± 0.24	−1.17
524.6773	49005.847	1.5	29951.816	0.5	0.26 ± 0.03	−2.37
524.9436	49351.734	2.5	30307.367	1.5	0.117 ± 0.026	−2.54
527.4975	51788.815	3.5	32836.653	3.5	1.24 ± 0.18	−1.38
527.9877	51788.815	3.5	32854.250	4.5	0.32 ± 0.05	−1.97
528.0070	51788.815	3.5	32854.940	2.5	0.26 ± 0.05	−2.06
530.5865	49706.261	2.5	30864.433	2.5	0.48 ± 0.10	−1.91
530.8421	51669.406	2.5	32836.653	3.5	0.47 ± 0.07	−1.92
531.0692	51669.406	2.5	32844.707	1.5	0.23 ± 0.03	−2.23
531.3581	51669.406	2.5	32854.940	2.5	0.94 ± 0.14	−1.62
531.8388	48749.278	0.5	29951.816	0.5	0.16 ± 0.03	−2.87
533.4868	51584.100	1.5	32844.707	1.5	1.10 ± 0.17	−1.72
533.7783	51584.100	1.5	32854.940	2.5	0.27 ± 0.05	−2.33
540.7615	49351.734	2.5	30864.433	2.5	0.25 ± 0.06	−2.18
542.0925	48749.278	0.5	30307.367	1.5	0.45 ± 0.06	−2.40
547.8374	51942.664	4.5	33694.142	5.5	0.33 ± 0.05	−1.82
550.2086	51788.815	3.5	33618.936	4.5	0.30 ± 0.05	−1.96
550.3224	51584.100	1.5	33417.981	2.5	0.27 ± 0.05	−2.31
550.8623	51669.406	2.5	33521.090	3.5	0.29 ± 0.05	−2.11
551.0719	49005.847	1.5	30864.433	2.5	0.203 ± 0.027	−2.43
605.3469	54784.450	3.5	38269.569	3.5	0.15 ± 0.03	−2.17
642.1706	51669.406	2.5	36101.524	3.5	0.51 ± 0.09	−1.72

Notes.

^aWavelength values computed from energy levels using the standard index of air from Peck & Reeder (1972).

^bEnergy levels are from Sansonetti & Nave (2014).

(This table is available in its entirety in machine-readable form.)

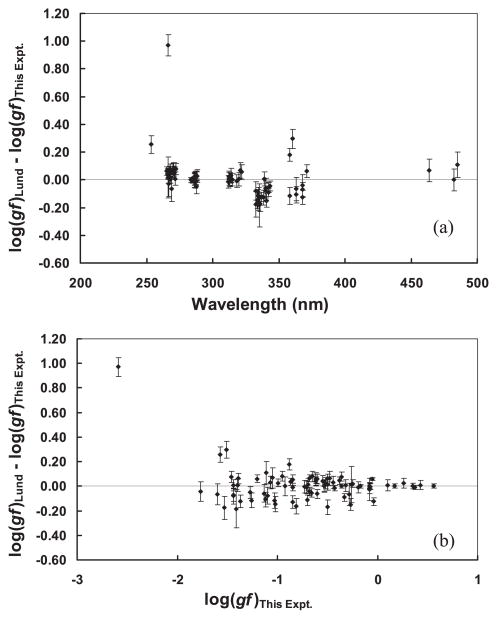
Nilsson et al. (2006) at Lund compared various published transition probabilities in their paper. We are thus focusing on the 102 lines in common with Nilsson et al. for our comparisons in Figure 1. The error bars in this figure are the transition probability uncertainties from both experiments combined in quadrature. Nilsson et al. did not provide separate BF uncertainties. Combined transition probability errors are slight overestimates of the uncertainties on the differences because both data sets have Schade et al. (1990) radiative lifetimes in common. However, those radiative lifetime uncertainties are small, typically less than 5%. The top panel of Figure 1 is typical of BF and transition probability comparisons. The BFs of weak lines are difficult to measure for the reasons discussed above. There are also a few outliers. The top panel of Figure 1 suggests that there are no serious differences in the relative radiometric calibration used by Nilsson et al. and in this work over a factor of two in wavelength.

Figure 1.

(a) Comparison of log(gf ) values for 102 lines from Nilsson et al. (2006) at Lund with our values, as a function of wavelength. The error bars are the uncertainties from Nilsson et al. combined in quadrature with the uncertainty from this experiment. The central line indicates perfect agreement. (b) The same except as a function of log(gf )_{This Expt.}

5. THE CHROMIUM ABUNDANCE IN THE SOLAR PHOTOSPHERE FROM Cr II TRANSITIONS

Sneden et al. (2016, hereafter S16) derived new chromium abundances in the Sun from both neutral and ionized transitions. For Cr I, their standard 1D LTE analysis yielded log ε(Cr I) = 5.650 ± 0.007 (σ = 0.068, 87 lines).⁹ Their derived Cr II abundance was nominally in agreement: log ε = 5.630 ± 0.030, but the line-to line scatter was large (σ = 0.153, from 13 lines). That analysis used transition probabilities mostly from Nilsson et al. (2006), supplemented with a few lines from (Gurell et al. 2010). Unfortunately, the Nilsson et al. and Gurell et al. studies reported gf values for just 12 lines in the optical spectral region (here, λ > 400 nm), and none with λ > 484 nm. This restriction leaves out many solar photospheric Cr II transitions that could be reliable chromium abundance indicators. The Moore et al. (1966) solar line compendium identifies 86 Cr II lines with λ > 400 nm, and 38 of these lines have λ > 484 nm; the S16 abundance analysis included only seven transitions with λ > 400 nm.

Our new derivation of the photospheric abundance from Cr II lines follows the procedures of our previous Fe-peak studies in this series. Our approach is described in Section 2 of S16, and additional details can be found in, e.g., Lawler et al. (2015) and Wood et al. (2014a). Here we apply these procedures to Cr II.

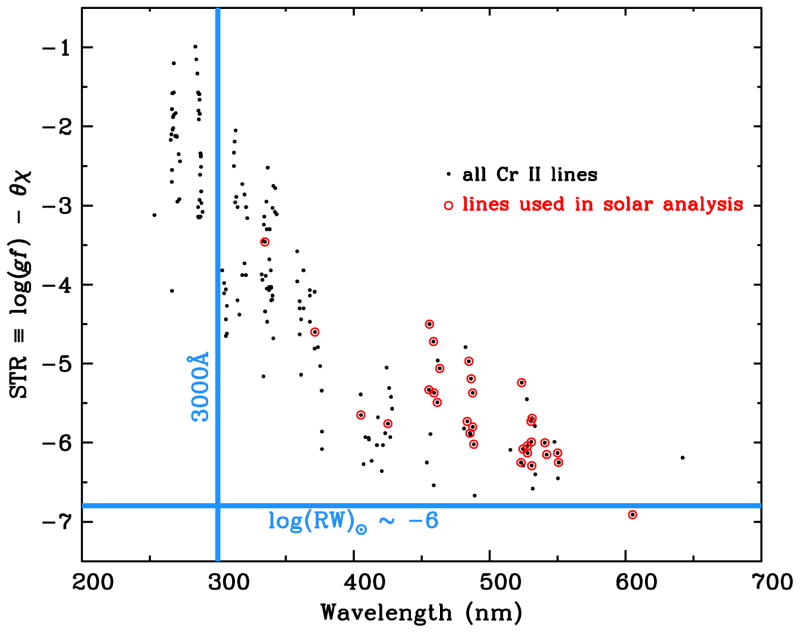
We begin with a theoretical assessment of the detectability of the Cr II lines, employing the same approximations of our previous papers in this series with a strength factor STR ≡ log(gf ) − θ_χ, where χ is the excitation potential (E. P.) in eV, and the inverse temperature is θ = 5040 K/T using an effective photospheric temperature T in Kelvin. The STR is approximately the log of the equivalent width of a photospheric line with a simple additive offset. A further simplification is our adoption of θ= 1, as in previous papers of this series. The log(gf ) values are those of Table 4. The STR values for our Cr II lines are plotted as a function of wavelength in Figure 2, using red circles to denote those lines that are employed in our solar abundance analysis. A horizontal blue line indicates the approximate STR value of Cr II lines that have extremely small reduced equivalent widths log(RW) = log(EW/λ) ≈ −6.0. Almost all of our lines are much stronger than this rough weak-line limit. In fact, the line at 605.3 nm, predicted to be the weakest of all measured Cr II lines, is easily detected at log(EW/λ) = log(4.5 × 10⁻⁴ nm/605.3 nm) ≈ −6.1, and is used in our solar analysis. Therefore we retain all lines of Table 4 for potential use in solar and stellar spectra.

Figure 2.

Relative strengths STR of Cr II lines vs. line wavelength. This figure is constructed in the same manner as Figure 5 of Lawler et al. (2015). The vertical blue line indicates the 3000 Å atmospheric cutoff, and the horizontal blue line is placed where the STR values approach the practical weak-line limit in the photospheric spectrum (reduced widths log(RW ) = −6) for abundance analysis. The black points include all 183 transitions with laboratory data reported here, and those points encircled in red indicate those lines used in our solar abundance determination.

Final line selection for the solar photospheric analysis is accomplished by a straightforward elimination of those Cr II lines that are either too blended with other atomic and/or molecular (CH, CN, OH) contaminants, or are too strong (saturated) to be sensitive to chromium abundance variations. An example of a line rejected for blending problems is that of 461.88 nm: it should be strong in the solar spectrum, but the Moore et al. (1966) solar line compendium indicates that there is also an Fe I line at this wavelength. Our synthetic spectrum computations (see below) suggest that the relative contributions of these two species to the total absorption feature are approximately equal, rendering the derived chromium abundance from it entirely dependent on the correct treatment of the Fe I contaminant. This line is discarded from the solar analysis. Many promising Cr II lines with λ < 350 nm are also hopelessly blended, but the few without significant contamination problems are too strong. An example here is the line at 336.81 nm: Moore et al. list its EW as 1.7 × 10⁻² nm, or log (EW/λ) ≈ −4.2, placing it on the flat/damping part of the curve-of-growth for this line. It therefore is only weakly sensitive to chromium abundance changes. This line is also discarded.

In the end, 31 out of the original 183 Cr II transitions from Table 4 survive to participate in the solar abundance calculations. Again referring the reader to S16 for computational details, we derive line abundances from comparisons of observed (Delbouille et al. 1973)¹⁰ and synthetic photospheric spectra. The synthetic spectra are computed with the current version of the 1D/LTE analysis code MOOG (Sneden 1973).¹¹ To keep consistency with our previous papers on iron-group and neutron-capture element transition data, we used the model solar photosphere of Holweger & Müller (1974), adopting a microturbulence ν_t = 0.85 km s⁻¹. The creation of atomic and molecular line lists with the latest laboratory data also has been described in previous papers of this series. S16 note that although chromium has five naturally occurring isotopes, nearly 84% of the element exists as ⁵²Cr in the solar system. Moreover, our inspection of very high-resolution laboratory spectra does not reveal any detectable line broadening that could be attributed to isotopic and/or hyperfine substructure. Therefore, the Cr II lines in our syntheses are treated as single absorption features.

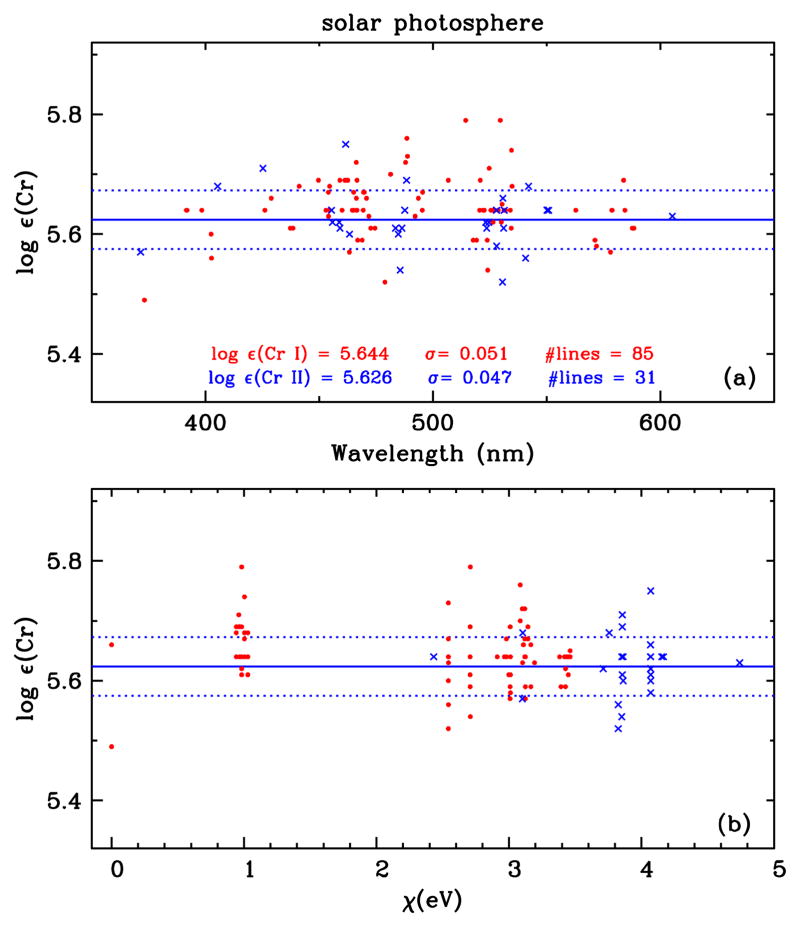
Table 5 lists the transition parameters and derived photospheric abundances for the Cr II lines. These yield a mean abundance 〈logε(Cr II)〉 = 5.626 ± 0.009 (σ = 0.047; 31 lines), where log ε(Cr II) means the chromium elemental abundance determined from Cr II. Our new value is statistically the same as that reported by S16: 5.630 ± 0.030 (σ = 0.153; 13 lines). However, with double the number of lines and one-third the line-to-line scatter of the earlier result, our new abundance is obviously more reliable; it is a more robust estimate of the photospheric chromium abundance.

Table 5.

Cr II Line Abundances in the Sun and HD 84937

λ nm (air)	λ (eV)	log(gf )	log ε Sun	log ε HD 84937
265.358	1.491	−0.68	...	3.52
266.172	1.505	−1.20	...	3.42
266.601	1.505	−0.08	...	3.32
266.871	1.491	−0.55	...	3.47
267.181	1.505	−0.38	...	3.47
267.283	1.524	−0.50	...	3.47
267.879	1.491	−0.36	...	3.50
268.709	1.505	−0.62	...	3.52
269.104	1.548	−0.28	...	3.50
269.841	1.524	−0.60	...	3.38
269.868	1.482	−0.65	...	3.38
272.275	1.491	−0.95	...	3.46
284.983	1.505	0.17	...	3.54
285.676	2.432	−0.59	...	3.42
285.865	2.419	−0.73	...	3.42
286.510	1.505	−0.08	...	3.35
286.533	2.419	−0.71	...	3.42
286.674	1.491	−0.17	...	3.45
286.709	2.432	−0.50	...	3.40
286.765	1.482	−0.36	...	3.40
287.043	2.453	−0.16	...	3.36
287.381	2.432	−0.69	...	3.34
287.599	2.481	0.12	...	3.32
287.624	1.505	−0.87	...	3.46
287.798	1.524	−0.99	...	3.45
287.845	1.548	−1.27	...	3.43
288.919	2.481	−0.60	...	3.37
303.292	2.704	−1.13	...	3.40
311.865	2.419	−0.08	...	3.42
312.037	2.432	0.10	...	3.40
312.498	2.453	0.26	...	3.36
312.870	2.432	−0.53	...	3.41
313.206	2.481	0.43	...	3.42
313.669	2.453	−0.44	...	3.42
314.723	2.481	−0.53	...	3.47
318.070	2.541	−0.19	...	3.37
320.859	2.541	−1.35	...	3.47
320.918	2.542	−0.48	...	3.37
332.406	2.432	−1.44	...	3.42
332.835	2.419	−1.53	...	3.39
333.633	2.419	−1.02	...	3.35
333.980	2.432	−0.81	...	3.37
334.258	2.453	−0.70	...	3.39
334.783	2.432	−1.03	5.64	3.38
335.312	2.481	−1.41	...	3.42
335.850	2.453	−0.50	...	3.37
336.029	3.101	−0.20	...	3.37
336.176	3.103	−0.95	...	3.44
336.371	2.432	−2.04	...	3.47
336.805	2.481	−0.04	...	3.35
337.833	3.101	−0.98	...	3.47
337.937	3.103	−0.93	...	3.45
337.982	3.103	−0.58	...	3.40
338.268	2.453	−0.85	...	3.40
339.143	2.419	−1.40	...	3.45
339.384	3.103	−0.94	...	3.45
339.429	3.103	−0.93	...	3.45
340.326	3.103	−1.10	...	3.34
340.332	2.432	−0.60	...	3.34
340.877	2.481	−0.27	...	3.34
342.121	2.419	−0.66	...	3.39
342.274	2.453	−0.33	...	3.37
343.331	2.432	−0.68	...	3.37
358.550	2.704	−1.26	...	3.40
360.361	2.704	−1.60	...	3.38
363.168	2.704	−1.60	...	3.50
371.295	2.704	−1.39	...	3.42
371.517	3.101	−1.50	5.57	3.40
405.408	3.103	−2.56	5.68	...
425.263	3.855	−1.90	5.71	...
455.499	4.068	−1.27	5.64	...
455.864	4.070	−0.43	5.62	3.47
458.820	4.068	−0.65	5.62	3.47
459.205	4.070	−1.30	5.61	3.49
461.662	4.069	−1.42	5.75	...
461.881	4.070	−0.89	...	3.45
463.407	4.069	−1.05	5.60	3.47
482.413	3.868	−0.92	...	3.49
483.623	3.855	−1.87	5.61	...
484.825	3.861	−1.11	5.60	3.42
485.619	3.851	−2.03	5.54	...
486.433	3.855	−1.34	5.61	...
487.640	3.851	−1.52	5.64	...
487.649	3.861	−1.94	5.64	...
488.460	3.855	−2.16	5.69	...
523.250	4.068	−2.18	5.62	...
523.732	4.070	−1.17	5.61	...
524.677	3.711	−2.37	5.62	...
527.988	4.070	−1.97	5.64	...
528.007	4.070	−2.06	5.58	...
530.586	3.824	−1.91	5.52	...
530.842	4.068	−1.92	5.66	...
531.069	4.069	−2.23	5.61	...
531.358	4.070	−1.62	5.64	...
540.762	3.824	−2.18	5.56	...
542.092	3.755	−2.40	5.68	...
550.209	4.165	−1.96	5.64	...
550.862	4.153	−2.11	5.64	...
605.347	4.741	−2.17	5.63	...

There are no new lab data for Cr I transitions, but we revisit the S16 solar photospheric line selections and compute new synthetic spectrum for many lines of this species. These new analyses result in elimination of two lines that were used in S16 but are deemed too uncertain to be included in the present study. Table 6 contains the revised Cr I data for 85 lines, from which we derive 〈log ε(Cr I)〉 = 5.644 ± 0.006 (σ = 0.051). This is nearly identical to the result of S16, and is in good agreement with our new Cr II abundance.

Table 6.

Cr I Line Abundances in the Sun and HD 84937

λ nm (air)	λ eV	log(gf )	log ε Sun	log ε HD 84937
288.92	1.029	−0.26	...	3.40
289.68	0.982	−0.85	...	3.47
297.55	0.968	−0.45	...	3.52
298.87	0.941	−0.47	...	3.32
299.66	0.982	−0.28	...	3.32
300.51	1.029	−0.25	...	3.37
301.85	0.968	−0.44	...	3.42
302.16	1.029	0.61	...	3.37
303.70	1.029	−0.32	...	3.49
305.39	1.029	−0.15	...	3.37
357.87	0.000	0.42	...	3.15
359.35	0.000	0.31	...	3.15
360.53	0.000	0.17	...	3.17
374.39	2.542	0.29	...	3.37
373.20	0.000	−2.57	5.49	...
388.52	0.968	−1.35	...	3.40
390.88	1.003	−1.05	...	3.40
391.63	0.968	−1.75	5.64	...
391.92	1.029	−0.71	5.64	3.42
392.86	1.003	−1.31	...	3.40
396.37	2.542	0.62	...	3.42
398.43	2.543	−0.47	5.64	...
402.50	2.542	−1.05	5.60	...
402.71	2.543	−0.95	5.56	...
425.43	0.000	−0.09	...	3.22
426.14	2.911	−0.69	5.64	...
427.48	0.000	−0.22	...	3.22
428.97	0.000	−0.37	5.66	3.22
434.45	1.003	−0.65	...	3.32
437.13	1.003	−1.27	...	3.37
437.33	0.982	−2.30	5.61	...
438.50	1.029	−1.41	5.61	...
441.22	1.029	−2.67	5.68	...
449.68	0.941	−1.14	5.69	3.32
452.98	2.542	−1.35	5.64	...
454.05	2.542	−0.52	5.67	...
454.11	2.543	−1.15	5.63	...
454.46	2.542	−0.59	5.64	...
454.53	2.542	−1.30	5.64	...
454.60	0.941	−1.37	5.68	3.42
459.14	0.968	−1.74	5.69	...
460.07	1.003	−1.25	5.64	3.37
461.34	0.960	−1.65	5.69	...
461.61	0.982	−1.19	5.69	3.32
462.62	0.968	−1.33	5.69	3.41
463.33	3.123	−1.11	5.57	...
464.62	1.029	−0.74	5.64	3.37
465.13	0.982	−1.46	5.64	3.42
465.22	1.003	−1.04	5.67	3.37
466.33	3.099	−0.56	5.72	...
466.38	3.108	−0.39	5.66	...
466.48	3.123	−0.30	5.64	...
466.62	2.965	−0.88	5.64	...
466.65	3.142	−0.34	5.69	...
466.93	3.165	−0.47	5.59	...
468.94	3.123	−0.40	5.59	...
469.40	2.980	−0.80	5.64	...
469.52	2.980	−1.12	5.67	...
469.85	3.142	−0.11	5.67	...
470.80	3.165	0.07	5.66	...
471.84	3.193	0.24	5.63	...
472.72	2.998	−0.65	5.61	...
474.53	2.706	−1.38	5.61	...
478.93	2.542	−0.33	5.52	...
481.43	3.085	−1.22	5.70	...
488.01	3.119	−1.58	5.72	...
488.60	3.085	−1.12	5.76	...
488.85	2.542	−1.36	5.73	...
492.23	3.102	0.38	5.63	...
493.63	3.110	−0.25	5.66	...
495.37	3.119	−1.48	5.64	...
495.48	3.119	−0.17	5.67	...
506.77	2.707	−1.07	5.69	...
514.47	2.708	−1.37	5.79	...
517.74	3.426	−0.53	5.59	...
519.20	3.392	−0.40	5.59	...
520.45	0.941	−0.19	...	3.32
520.60	0.941	0.02	5.64	3.27
520.84	0.941	0.17	5.69	3.27
522.09	3.382	−0.89	5.64	...
522.58	2.706	−1.50	5.64	...
523.90	2.707	−1.27	5.59	...
524.15	2.708	−1.92	5.54	...
524.76	0.960	−1.59	5.71	...
525.51	3.461	−0.10	5.64	...
526.52	3.426	−0.35	5.62	...
526.57	0.968	−1.71	5.64	...
527.20	3.447	−0.42	5.64	...
528.72	3.435	−0.87	5.64	...
529.67	0.982	−1.36	5.79	...
530.07	0.982	−2.00	5.62	...
530.42	3.461	−0.67	5.65	...
531.29	3.447	−0.55	5.64	...
531.88	3.435	−0.67	5.64	...
534.05	3.435	−0.73	5.64	...
534.48	3.447	−0.99	5.61	...
534.58	1.003	−0.95	5.74	3.37
534.83	1.003	−1.21	5.68	3.34
540.98	1.029	−0.67	...	3.25
562.86	3.419	−0.74	5.64	...
571.28	3.008	−1.03	5.59	...
571.98	3.011	−1.58	5.58	...
578.12	3.008	−1.00	5.57	...
578.70	3.011	−1.55	5.64	...
578.84	3.011	−1.49	5.64	...
583.87	3.009	−1.82	5.69	...
584.46	3.011	−1.77	5.64	...
587.65	3.008	−2.05	5.61	...
588.44	3.011	−1.86	5.61	...

The Cr I and Cr II photospheric line abundances are plotted as functions of wavelength and excitation energy in Figure 3. There is no apparent correlation of line abundance with wavelength (panel (a)). However, the wavelength range of useful lines is limited to only part of the optical spectrum, about 400–600 nm. Line abundance versus lower excitation energy (panel (b)) also reveals no clear trend. Unfortunately nearly all Cr II lines used in the solar abundance study arise from energy levels near 4 eV, thus little new information is seen in this panel.

Figure 3.

Solar photospheric abundances for Cr I and Cr II lines plotted as functions of wavelength (panel (a)) and excitation potential (panel (b)). The statistics for the mean abundances for Cr I (red dots) and Cr II (blue x’s) are written in panel (a). In each panel blue solid lines indicate the mean Cr II abundance, and blue dotted lines indicate ±σ deviations from the mean.

Our photospheric chromium abundances, 〈log ε〉 = 5.64 and 5.62 from Cr I and II, respectively, are in good agreement with recent literature spectroscopic and meteoritic values, as summarized in Table 2 of S16. Scott et al. (2015) have thoroughly explored the dependence of photospheric abundances of Fe-peak elements on various modeling assumptions, and their discussion will not be repeated here. Their recommended chromium abundance is log ε = 5.62, from consideration of NLTE line formation and multidimensional solar atmospheres. Of most interest here is that they derive log ε = 5.65 from an LTE analysis using the Holweger & Müller (1974) model, which is closest to our abundance assumptions. Further solar spectroscopic chromium modeling studies would be interesting but are beyond the scope of this paper.

6. THE CHROMIUM ABUNDANCE OF HD 84937

Ionized chromium has not been featured in abundance surveys of low metallicity stars because this species has only a few strong transitions in the visible spectral range, λ>3400 nm. Among large-sample abundance surveys of very low metallicity stars, only Honda et al. (2004), Lai et al. (2008), and Roederer et al. (2014) have included Cr II lines in a systematic fashion. All of these studies (and analyses of individual stars published in other papers) considered the 455.87 and 458.82 nm lines. To these lines Lai et al. added measurements of the 311.87, 312.87, 371.52, and 484.82 nm lines, and Roederer et al. added the 340.87 and 459.20 nm lines. To our knowledge, the S16 study of the well-known metal-poor halo star HD 84937 is the only one to include a large number (78) of Cr II lines.

With our new lab transition data we repeat the chromium abundance computations of S16. As in our previous lab/stellar studies of Fe-peak elements, we choose this star (a) for its well-determined atmospheric parameters, (b) for its available high-resolution spectra ranging from the vacuum ultraviolet (UV) to the very red (230–800 nm), and (c) for the higher electron and H density of a metal-poor dwarf compared to those of a metal-poor red giant. Earlier papers in this series have given details of atmospheric parameter determinations, and as before we adopt a model interpolated in the Kurucz (2011) model atmosphere grid¹² with effective temperature T_eff = 6300 K, gravity log (g) = 4.0, overall model metallicity [Fe/H] = −2.15, and microturbulent velocity ν_t = 1.5 km s⁻¹. For stars in this atmospheric parameter domain, calculated departures from LTE in Fe metallicity estimates are not large. Bergemann et al. (2012) consider Fe I and II line formation in the Sun, Procyon, HD 84937, and several other metal-poor stars. They adopt T_eff = 6408 K and log(g) = 4.13 for HD 84937, not too different from our values. Their derived microturbulence, v_t ≡ 1.4 km s⁻¹, is also similar to our number. From their data in Table 3 for the Sun and HD 84937, we derive [Fe I/H] = −2.11 and [Fe II/H]= −2.12 with the MARCS (Gustafsson et al. 2008) models. Their application of LTE and NLTE analyses with various model assumptions typically raise these metallicities by about 0.06 dex for Fe I and about 0.03 dex for Fe II.

With a metallicity more than two orders of magnitude less than the Sun, HD 84937 presents a very weak-lined spectrum. This necessitates a fresh Cr II line selection process. Many useful solar Cr II lines in the λ > 450 nm domain are undetectably weak in HD 84937. In compensation, many lines with λ< 400 nm that are too saturated/blended for solar abundance analysis (or lie in the vacuum UV) are relatively unsaturated and do not suffer much contamination from other species in HD 84937.

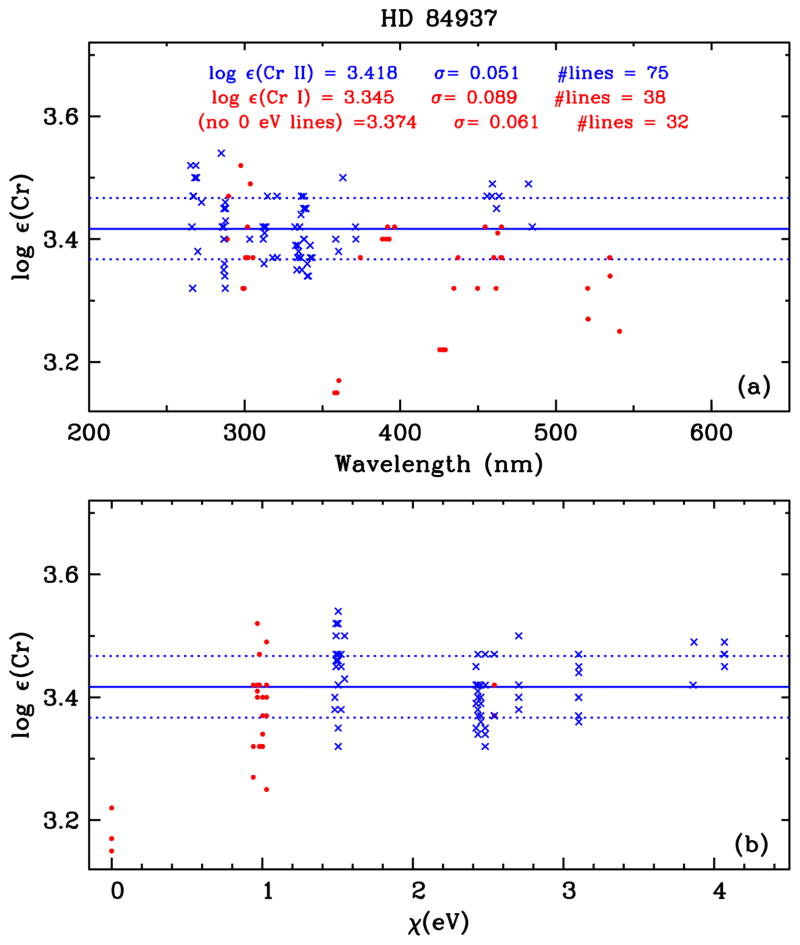
Searching for lines from Table 4 in our optical ESO VLT UVES and HST/STIS UV high-resolution spectra (see S16) yields 80 Cr II transitions. We perform synthetic spectrum analyses in the same manner as we have done for the solar photosphere. For this metal-poor star we use the MOOG version that includes continuum scattering in the source function (Sobeck et al. 2011), but the scattering is negligible; H⁻ is dominant, with H I Balmer continuum opacity contributing in the near-UV spectral region. In the end we retain 75 Cr II lines for HD 84937; their parameters and abundances are listed in Table 5. From these we derived a mean abundance 〈log ε(Cr II)〉 =3.418 ± 0.006 (σ = 0.051). In Figure 4 we plot the Cr II line abundances versus wavelength and excitation energy; no substantial trends with either quantity are present.

Figure 4.

HD 84937 abundances for Cr I and Cr II lines plotted as functions of wavelength (panel (a)) and excitation potential (panel (b)). The definitions of points and lines in this figure are the same as in Figure 3. The statistics for the HD 84937 mean abundances are written in the top panel, and we show the Cr I mean with and without inclusion of the six E.P. = 0 eV transitions, which clearly yield very low abundances.

The decrease from the initial list of 80 transitions to the final list of 75 deserves comment. Three of the lines are discarded because we find them to be too blended for reliable chromium abundance estimates. We are unable to identify contamination issues with lines at 265.86 and 286.09 nm, even though they yield abundances that are 0.2–0.3 dex higher than nearly all of the useful chromium abundance indicators for HD 84937.

However, the 265 and 286 nm lines are members of prominent Cr II multiplets that have been studied for decades, being catalogued in the Ultraviolet Multiplet Table (Moore 1952, p. 6). The 265 nm line belongs to Moore’s UV multiplet 8 (⁶D–⁶D). Table 4 includes 13 members of this multiplet; we report abundances in Table 5 for eight of them, leading to a mean abundance 〈log ε〉 = 3.46 (σ = 0.08). However, the 265 nm transition indicates log ε = 3.67, more than 2σ from the multiplet mean. Neither the transition probability of this line nor its emission intensity in the Moore table suggests that it should be much stronger than other multiplet partners. We conclude that the 265 nm line is contaminated by a blending agent not included in our synthetic spectrum line list, and we drop it from further consideration.

The same arguments can be applied to the line at 286 nm, a member of Moore’s (1952) UV multiplet 5 (⁶F–⁶D). As in the previous case, Moore gives transition data for 13 multiplet 5 members, and we report abundances in Table 5 for eight of them. The mean abundance is 〈log ε〉=3.42 (σ = 0.06). But for 286.09 nm the derived abundance is 3.72, far from the multiplet mean. The transition probability of this line and the emission intensity given by Moore do not predict the large absorption strength of 286 nm seen in HD 84937, so it too must have a contaminant that is not in our synthetic spectrum line list. We also discard this line.

Our new chromium abundance, 〈log ε(Cr II)〉=3.417±0.006 (σ = 0.050, 75 lines), is similar to that reported by S16: 3.437 ± 0.008 (σ = 0.097, 78 lines). However, the lines making up these two mean abundances are somewhat different and systematic uncertainties, which vary from line-to-line, can overwhelm the small statistical uncertainties. There are 67 Cr II lines in common between S16 and the present study, which means that we do not include 11 lines reported in S16 and we have 7 lines not employed by S16 (compare Table 5 with their Table 4). The agreement between old and new abundances affirms that the transition probabilities from Nilsson et al. (2006) and Gurell et al. (2010) are similar to our new values for the Cr II lines that are useful abundance indicators in HD 84937.

As done for the solar photosphere in Section 5, we looked again at the Cr I lines in HD 84937, and were able to identify 38 usable transitions. Our derived mean abundance is 〈log ε(Cr I)〉=3.345±0.014 (σ = 0.089), which is somewhat larger than that reported by S16, 3.304 ± 0.018 (σ = 0.098). More importantly, both values have large internal dispersion and are not in very good agreement with the Cr II abundances of either study. The cause can easily be seen in panel (b) of Figure 4. Although the Cr II lines show satisfactorily small scatter with negligible trends in wavelength and excitation energy, the six Cr I lines included here¹³ that arise from its ground level (χ = 0 eV) yield much smaller abundances than all other chromium transitions. From Table 6 we compute 〈log ε(Cr I, 0 eV)〉 = 3.19 ± 0.01 (σ = 0.04), while for the other 32 Cr I lines 〈log ε(Cr I, >0 eV)〉 = 3.374 ± 0.011 (σ = 0.061).

The Cr I resonance (χ = 0 eV) transitions near 360 nm are rarely employed in large-sample abundance surveys of metal-poor stars. However, the Cr I violet resonance triplet lines of the 425.43, 427.48, and 428.97 nm lines figure prominently in such studies. For example, McWilliam et al. (1995) and Cayrel et al. (2004) used these lines and four weaker ones (not all of which were detectable in all stars). Barklem et al. (2005) relied exclusively on the violet triplet. Yong et al. (2013) used these and just two higher-excitation Cr I lines. Thus, the violet triplet has been the dominant indicator of chromium abundances in metal-poor stars. Only Roederer et al. (2014) systematically measured up to nine higher-excitation Cr I lines, thus muting somewhat the influence of the violet triplet on the derived mean abundances. It is clear that the clash between derived Cr I and Cr II abundances in very metal-poor stars (e.g., Kobayashi et al. 2006, Figures 20 and 21) can be traced to this issue.

Of course, this leads one to consider the reliability of log(gf ) data for resonance lines of Cr I. The BFs of the transitions near 360 nm and the violet triplet of 425.43, 427.48, and 428.97 nm are all nearly 1.0 and thus make no significant contribution to the log(gf ) uncertainty. Furthermore, the z⁷P upper levels of the violet triplet have multiple independent radiative lifetime measurements using LIF techniques with extremely good agreement at the 0.01–0.02 dex level (Cooper et al. 1997; Sobeck et al. 2007 and references therein). The y⁷P upper levels of the 360 nm triplet have fewer measurements but these lifetimes of 6.6 ns are likely to be similarly accurate (Cooper et al. 1997). Since the log(gf ) data look to be very reliable, it seems likely that there is some deviation from LTE involving the ground level of the neutral. This NLTE effect on the neutral ground-level population of Cr appears to be quite similar to the NLTE effect on the neutral ground-level population of Mn (S16).

As in previous papers of this series, we find that the internal line-to-line scatter uncertainties for HD 84937 are ≤0.04 dex. We vary the input model atmospheres for typical Cr II lines and find that if T_eff is increased by 150 K, then on average Δ(log ε) ≡ +0.05; if log(g) is increased by 0.3, then Δ(log ε) ≡ +0.09; if the metallicity is decreased to [Fe/H] = −2.45, then Δ(log ε) ≡ 0.00 (unchanged); and if v_t is decreased to 1.25 km s⁻¹ then Δ (log ε) = +0.00 to +0.07, depending on the strength of the measured transition. These responses to atmospheric uncertainties are similar to those found for V II (Wood et al. 2014a) and Ti II (Wood et al. 2013). This means that [Cr/V] or [Cr/Ti] relative abundance ratios that are based on ionized transitions are insensitive to model parameter variations.

Bergemann & Cescutti (2010) made extensive computations to estimate NLTE effects on abundances derived from Cr I and Cr II lines in the Sun and some metal-poor stars, including HD 84937. Their computations suggest large departures from LTE in Cr I, in the sense that the LTE abundances are too low by typically 0.1–0.3 dex. For HD 84937, they used nine Cr I lines to derive a recommended mean correction of +0.25 dex to the LTE value. In contrast, for Cr II they found only small NLTE abundance corrections, which are always less than 0.1 dex. They derived a mean correction of +0.06 dex from two Cr II lines in HD 84937. Unfortunately, the Cr II lines in their study included only those with high lower excitation energies, χ ≈ 4 eV. Most of our lines arise from levels 1.5 to 2.5 eV. It would be of interest in the future to extend the Bergemann & Cescutti computations to this energy range. At any rate, NLTE effects on Cr II lines in HD 84937 appear to be very small.

In addition to the NLTE effects on resonance lines of Mn I and Cr I discussed above, a third NLTE and/or 3D effect described as a “Balmer Dip” in abundance values appears in HD 84937. This expression refers to a dip, ≈0.2 dex, in the abundance value for lines with wavelengths in the vicinity of, and somewhat below, the Balmer limit at 364.5 nm. Roederer et al. (2012) observed the Balmer Dip in this wavelength region using Fe I lines during studies of four metal-poor stars. Several unsuccessful attempts were made to explain the Balmer Dip including tests of various approximations for terminating the Balmer series and selection of a subset of Fe I lines with the most reliable log(gf ) values. Wood et al. (2013) observed the Balmer Dip in HD 84937 using newly measured log(gf ) values for lines of Ti II. The relatively large number of Ti II lines in the Balmer continuum wavelength region enabled Wood et al. to make “cuts” through abundance data to reveal that the Balmer Dip is primarily due to lines with E. P. values above 1.2 eV. Interestingly, the Ti II lines contributing to the dip are thought to have highly reliable log(gf ) values because the lines are fairly strong branches that are relatively easy to measure and already have redundant BF measurements (Pickering et al. 2001; Wood et al. 2013). The possibility that the Balmer Dip is a combination of an NLTE and 3D effect is now being explored. Although NLTE effects are detectable in HD 84937, the vast majority of the first and second spectra lines of Fe-peak elements yield consistent abundance values (S16). Possible correlations of the Cr abundance with the abundance values of other Fe-peak elements are discussed in the next section.

7. CHROMIUM AND THE OTHER IRON-PEAK ELEMENTS

The Fe-peak element chromium is produced in explosive nucleosynthesis in core-collapse supernovae (CCSNe) primarily during “incomplete Si burning” (e.g., Nakamura et al. 1999; Nomoto et al. 2013). We have previously provided new abundance data for several Fe-peak elements in the Sun and HD 84937 in several recent papers (S16 and references therein). Evidence of a correlation among Sc, Ti, and V was found (S16) in the data of Roederer et al. (2014). Examination of additional data sets from Yong et al. (2013), Barklem et al. (2005), and Cayrel et al. (2004) further support the correlation between Sc and Ti. However, current CCSNe models have difficulty producing such correlations among these elements (e.g., S16). In a manner similar to that followed in Sneden et al., we have compared the Cr abundances of Roederer et al. (2014) with our new Cr value for HD 84937 and with other Fe-peak elements.

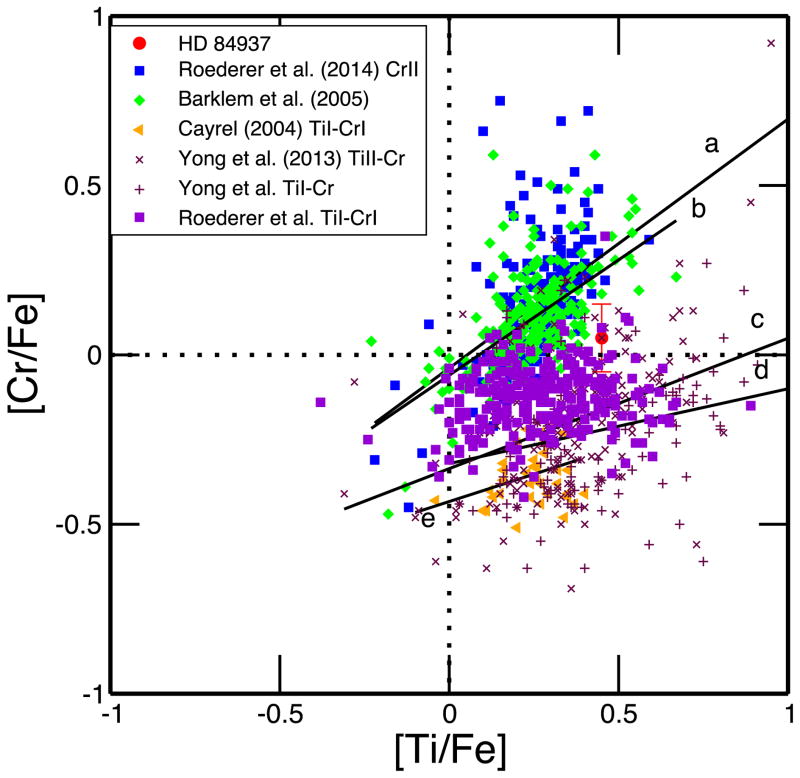
Examination of the Cr data shown in Figure 5 also suggests a correlation between this element and Ti. We have plotted the metal-poor stellar abundance data sets from Roederer et al. (2014), Barklem et al. (2005), Yong et al. (2013), and Cayrel et al. (2004), and have included results from both neutral and ionized Cr and Ti lines. The symbols and lines are defined in the figure legend. The solid black lines are linear regression fits to five individual stellar data sets: Roederer et. al (2014, Cr II, line a), Barklem et al. (2005, Cr I, line b), Yong et al. (2013, Cr II, line c), Yong et al. (Cr I, line d), and Cayrel et al. (2004, Cr I, line e). We chose not to do a linear regression for the neutral Cr–Ti data points from Roederer et al., as they show large star-to-star scatter in Cr I abundances at all Ti I values.

Figure 5.

Abundance ratios [Cr/Fe] vs. [Ti/Fe]. The filled squares are Cr II and Cr I from Roederer et al. (2014), the filled diamonds are Cr II from Barklem et al. (2005), left-facing triangles are Cr I from Cayrel et al. (2004), crosses are Cr II and pluses are Cr I from Yong et al. (2013), and the filled circle for HD 84937 is the ratio of the mean Cr derived in this paper with the mean Ti from S16. The horizontal and vertical (dotted) lines denote the solar abundance ratios of these elements. The (sloping) black straight lines are linear regression fits to the data from Roederer et al. (2014) Cr II (line a), Barklem et al. (2005) Cr I (line b), Yong et al. (2013) Cr II (line c), Yong et al. Cr I (line d), and Cayrel et al. (2004) Cr I (line e).

Examination of Figure 5 reveals that abundances of ionized Cr lines from Roederer et al. (2014) and Yong et al. (2013), as well as those of neutral Cr lines from Barklem et al. (2005), are all clearly correlated with fairly steep regression lines. Other surveys, however, show weaker correlation with flatter regression lines. This may indicate that the Cr abundances derived from Cr I lines suffer from large errors due to NLTE effects (see the discussion of the resonance Cr I lines in Section 6). We caution, however, that more careful work needs to be done in comparing the neutral and ionized species to discern the details of correlations between Cr and the other iron-peak elements.

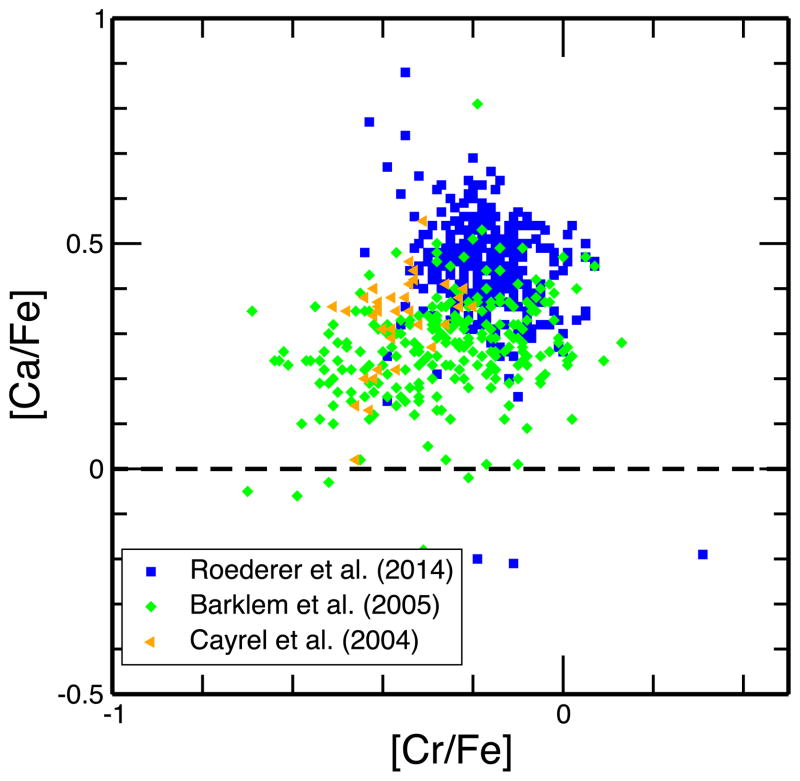
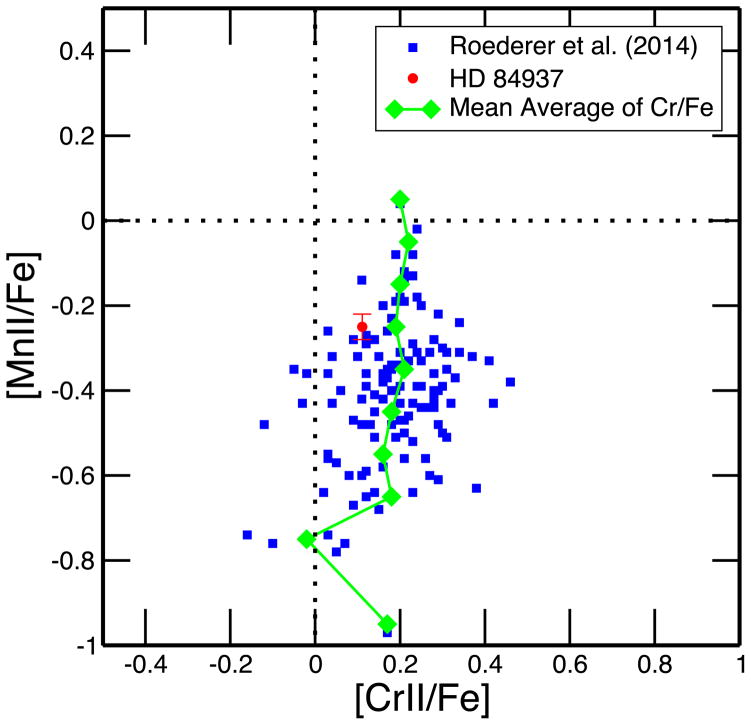
The behavior of Ca (the element just below the Fe peak) compared with the Fe-peak element Ti shows no such correlation as shown in Figure 6. Ca is an alpha element (Sneden et al. 2008) and it is expected to be produced mostly in explosive burning of oxygen (with some contribution from Ne burning) in massive stars (Thielemann et al. 1996), and thus has a different origin than the correlated iron-peak elements. We have also examined the abundances of Mn as a function of Cr (from the Roederer et al. data set) and show our results in Figure 7. To examine whether there was any correlation between the Cr and Mn data, we sorted the [Mn/Fe] data in 0.1 bins. The average values of Cr/Fe in those bins are shown as (green) filled diamonds in Figure 7. It is seen that the [Cr/Fe] value is almost constant, near 0.2 in all the bins (there were no data from approximately −0.9 to −0.81). Additional observational data sets also show no significant correlation in the Mn and Cr data. Thus, our analyses indicate that Cr production is correlated only with the other iron-peak elements Sc, Ti, and V. This, in turn, suggests that all four of these elements are made in a similar manner or together, but not in concert with other heavier iron-peak elements such as Mn, as shown in Figure 7, or Ni, or the alpha elements such as Ca, as shown in Figure 6. We reiterate the conclusions of S16 that the observed elemental abundance ratios of these iron-peak elements can be employed to explore the properties of explosive Si-burning and O-burning regions in, and to constrain models of, CC supernovae. Furthermore, as they noted, this makes clear how important it is to have precise abundances with small uncertainties and reliable atomic physics.

Figure 6.

Abundance ratios Ca/Fe vs. Cr/Fe from neutral transitions of each element. The symbols and lines are as in Figure 5.

Figure 7.

Abundance ratios Mn/Fe vs. Cr/Fe for the ionized transitions of each element. The filled circle for HD 84937 is the ratio of the mean Cr derived in this paper with the mean Mn from S16. The green filled diamonds represent average values of [Cr/Fe] within vertical bins of 0.1 in [Mn/Fe], with solid lines connecting the averages. The other symbols and lines are as in Figure 5.

8. SUMMARY

New emission BFs from data recorded using three FTS instruments and a 3 m focal length echelle spectrometer are used in combination with radiative lifetimes from new and published (Schade et al. 1990) LIF measurements to determine accurate, absolute atomic transition probabilities for 183 lines of Cr II. Applications of these new lab data yield Cr abundance values in the Sun and metal-poor star HD 84937 of 〈logε(Cr II)〉 = 5.626±0.009 (σ = 0.047, 31 lines) and 〈log ε(Cr II)〉 = 3.418 ± 0.006 (σ = 0.051, 75 lines), respectively, both using the Holweger & Müller (1974) 1D model. Saha balance in both the Sun and HD 84937 is confirmed with determinations of 〈log ε(Cr I)〉 = 5.644± 0.006 (σ = 0.051, 85 lines) and 〈log ε(Cr I, E.P.> 0 eV)> = 3.374 ± 0.011 (σ = 0.061, 32 lines), respectively. The resonance (E. P. = 0 eV) lines of Cr I yield a somewhat lower abundance value in HD 84937. A correlation of Cr (both neutrals and ions) with the iron-peak element Ti is found, suggesting an associated or related nucleosynthetic production. This is the heaviest iron-peak element (along with Ti, V and Sc) that appears to have a similar (or correlated) production history—none of the other iron-peak elements appear to be associated with Cr.