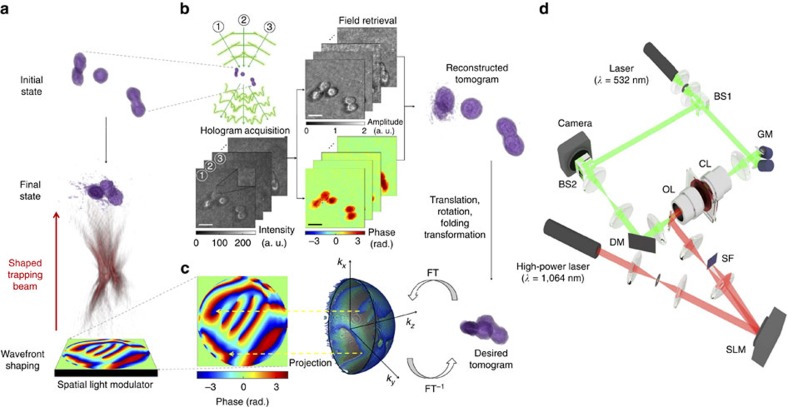
Figure 2. The working principle of TOMOTRAP.

(a) The overall process for the stable control of the orientation and shape of arbitrarily shaped particles using TOMOTRAP. (b) Real-time optical diffraction tomography reconstructing the 3D refractive index (RI) distribution of the samples from measured multiple holograms. Multiple holograms of the samples from various illumination angles are recorded by Mach-Zehnder interferometry, from which complex optical fields consisting of amplitude and phase delay of the sample are retrieved via a field retrieval algorithm. The optical diffraction tomography algorithm reconstructs the 3D RI distribution of samples from retrieved complex optical fields. The desired 3D beam intensity distribution is generated by applying rotational, translational and/or folding transformations to the reconstructed tomogram. Scale bar indicates 5 μm. (c) The 3D Gerchberg-Saxton algorithm calculates the phase-only 3D Fourier spectra of the desired 3D beam intensity obtained in b by applying iterative Fourier and inverse Fourier transforms (FT and FT⁻¹). The 2-D projection of the angular part of the 3D Fourier spectra yields a phase-only hologram to be displayed on a spatial light modulator used for holographic optical tweezers. (d) The optical setup for TOMOTRAP, consisting of optical diffraction tomography (green beam path) and holographic optical tweezers (red beam path). BS, beam splitter; GM, galvanomirror; CL, condenser lens; OL, objective lens; DM, dichroic mirror; SLM, spatial light modulator; SF, spatial filter.