Identification of Confirmatory Factor Analysis Models of Different Levels of Invariance for Ordered Categorical Outcomes

Abstract

This article considers the identification conditions of confirmatory factor analysis (CFA) models for ordered categorical outcomes with invariance of different types of parameters across groups. The current practice of invariance testing is to first identify a model with only configural invariance and then test the invariance of parameters based on this identified baseline model. This approach is not optimal because different identification conditions on this baseline model identify the scales of latent continuous responses in different ways. Once an invariance condition is imposed on a parameter, these identification conditions may become restrictions and define statistically non-equivalent models, leading to different conclusions. By analyzing the transformation that leaves the model-implied probabilities of response patterns unchanged, we give identification conditions for models with invariance of different types of parameters without referring to a specific parametrization of the baseline model. Tests based on this approach have the advantage that they do not depend on the specific identification condition chosen for the baseline model.

1. Introduction

Ordered categorical measures such as Likert scales are prevalent tools in psychology. Data collected with such measures had been analyzed as normal data until proper models for ordered categorical outcomes were introduced (Jöreskog and Moustaki, 2001; Mislevy, 1986; Muthén, 1984) and proved to be superior (Babakus, Ferguson and Jöreskog, 1987; Bernstein and Teng, 1989; Lubke and Muthén, 2004; Muthén and Kaplan, 1985). One of the most widely used models for ordered categorical outcomes is the threshold model (see, e.g. Muthén, 1984), where the ordered categories are considered a discretized version of a normally distributed latent continuous response through a number of threshold parameters. These thresholds indicate values of the latent continuous response where individuals cross over from one ordinal category to the next. Item response theory (IRT) gives an alternative framework of modeling ordered categorical data (e.g., Baker, 1992) and uses a different set of parameters. Invariance issues under IRT (differential item functioning) is not in the scope of this paper.

In this paper we are particularly concerned with the use of different identification conditions in the threshold model. An identification condition is a set of constraints imposed on the parameters of a model so that they can be uniquely estimated. More details will be discussed in Section 3. Similar to the common factors in a factor analysis model, the latent continuous responses for ordered categorical items are not directly observed and therefore have unknown scales. Constraints are needed to properly define their scales so that relevant parameters can be uniquely estimated. The most widely used option is to set the intercept of each latent response to zero and its variances to one (e.g., Christoffersson, 1975), which uses the δ-parametrization in Mplus (Muthén and Muthén, 1998–2012). Instead of setting the variances of the latent responses, one may set the variances of residuals to one in the θ-parametrization (e.g., Muthén and Christofferson, 1981) of Mplus. For both of these options, all thresholds are freely estimated. When the observed ordinal response contains three or more categories, one can set the scale of a latent response by constraining two thresholds to constants, typically through setting the first two thresholds to values of zero and one (Mehta, Neale and Flay, 2004). With this option, an intercept and a unique variance are estimated for each observed variable in addition to the remaining thresholds not constrained. Any of the three methods above can identify the model so that parameters can be estimated. Different identification conditions yield different parameter estimates but identical standardized parameter estimates and fit statistics. Changing identification condition simply rescales the latent continuous responses (or common factors), and has the same effect as any linear transformation of a variable.

Identification in multiple group analyses are considerably more complicated, as ordinal variables must be identified for each group in the analysis. When there is no constraint imposed across groups, each group is identified separately in the analysis and has its own scales, and parameters are in group-specific rather than shared units. Researchers interested in the invariance of parameters typically impose an identification condition across groups, with the goal of placing each group on the same scale. Subsequent tests of invariance (e.g., weak factorial invariance) are dependent on the chosen identification condition. If the constraints in the identification condition are not properly selected, invariance constraints and other tests of parameter equivalence may be inherently biased.

In this paper, we argue that constraints involved in common identification conditions are in and of themselves invariance constraints, restricting either the scale (mean and variance) or the allowed transformations applied to each group in an analysis regardless of unobserved group differences in scale. Because of this problem, we advocate a different approach to identifying multigroup models, where models with different invariance properties are identified on a case by case basis. We will give the identification conditions for models with different levels of invariance on a congeneric structure for categorical outcomes, and show that some of the invariance properties can not be tested alone without assuming other invariance properties. We will also discuss their implementation in common software packages as well as some technical issues.

This paper is organized as follows. The next section will review the basic concepts in modeling ordered categorical data and factorial invariance. This will be followed by a discussion of identification condition in Section 3 where the sources of non-identifiability are represented by transformations of parameters that leave the model implied probabilities unchanged. Using this group of transformations, Section 4 shows the problems of identifying an invariant model by simply incorporating additional constraints. We give identification conditions for models of different levels of invariance in Section 5 by exploiting the group of transformations in Section 3 and summarize the relationships among them in Sections 6 and 7 supported by a numerical illustration and simulation studies in Section 8. Software usage is briefly discussed next before closing.

2. CFA model for ordered categories and factorial invariance

2.1. The statistical model

Let y_j (j = 1, 2, ···, p) be the random variable of observed categorical response to item j, which takes K + 1 values 0, 1, ···, K. The threshold model (see, e.g. Muthén, 1984) assumes an underlying latent continuous response $y_j^{\ast }$ for y_j. The observed categorical response variable y_j arises from discretizing its corresponding latent response $y_j^{\ast }$ through thresholds τ_jk (j = 1, 2, ···, p; k = 0, 1, ···, K + 1), i.e.

$$y_j=k\text{if}{\tau }_{jk}<y_j^{\ast }<{\tau }_{j(k+1)}$$

where we assume τ_j0 = −∞ and τ_j(K+1) = ∞. The latent responses for all items ${\mathit{y}}^{\ast }={(y_1^{\ast },y_2^{\ast },\cdots ,y_p^{\ast })}^{\prime }$ follow a regular factor analysis model for continuous variables:

$${\mathit{y}}^{\mathbf{\ast }}=\mathit{\nu }+\mathbf{\Lambda }\mathit{\xi }+\mathit{\delta }$$

where ξ ~ N(κ, Φ) and δ ~ N(0, Θ) are the vectors of m common factors and p unique factors, ν is the p×1 vector of item intercepts and Λ is the p×m loading matrix. Note that in a factor analysis model, ξ and δ are uncorrelated and Θ is diagonal. This model implies the following expression for the covariance matrix Σ and mean vector μ of the latent response vector y^*:

$$\mathit{\mu }=\mathit{\nu }+\mathbf{\Lambda }\mathit{\kappa }\text{and}\mathbf{\sum }=\mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^{\prime }+\mathbf{\Theta }.$$ (1)

In a typical CFA model, the loading matrix Λ is assumed to be sparse and the locations and signs of the possible nonzero elements are known. In this paper, we only consider the case where Λ has a clustered structure, i.e., where each item loads only on one common factor. Because items with negative loadings are usually reverse-coded, we assume all nonzero loadings are positive. There are pK (finite) thresholds, p item intercepts, p loadings, p unique variances and m means, m variances and m(m − 1)/2 covariances of the common factors. The total number of parameters is p(K +3) +m(m+3)/2. When multiple groups are considered simultaneously with CFA models of the same configuration¹ but separate sets of parameters, we will use a superscript ^(g) for g = 1, 2, ···, G, where G is the total number of groups. In this case, the total number of parameters is G(p(K + 3) + m(m + 3)/2). These parameters are counted in the first row of Table 3 and Table 4 for polytomous and binary data. Of course, these parameters are not identified.

Table 3.

Model parameter counts (K >1). The 1st row counts all parameters. The 2nd through 4th rows list three parameterizations of a baseline model. The remaining rows list models whose invariant parameters are noted in Column 1. For all rows, $\frac{1}{2}m(m-1)G$ factor covariances are not listed but counted. Negative numbers are the number of constraints on diag(Σ). The entry with *** is pKG − (G − 1)(p + m).

	T	Λ	ν	diag(Θ)	κ	diag(Φ)	diag(Σ)	Total
Total	pKG	pG	pG	pG	mG	mG	0	G(p(K + 3) + m(m + 3)/2)
Condition 7	pKG	pG	0	pG	0	0	−pG
Condition 8	pKG	pG	0	0	0	0	0	G(p(K + 1) + m(m − 1)/2)
MYT	***	(p − m)G	0	pG	m(G − 1)	mG	−p
T	pK	pG	p(G − 1)	pG	0	0	−p	p(K − 2) + G(3p + m(m − 1)/2)
Λ	pKG	0	0	pG	0	0	0	same as baseline
ν or Θ	same as Condition 8							same as baseline
T & Λ	pK	p	p(G − 1)	pG	0	m(G − 1)	−p	G(2p + m(m + 1)/2) + p(K − 1) − m
T & ν	pK	pG	0	pG	mG	0	−p	G(2p + m(m + 1)/2) + p(K − 1)
T & Θ	pK	pG	p(G − 1)	p	0	0	−p	G(2p + m(m − 1)/2) + p(K − 1)
Λ & ν	same as loading invariance							same as baseline
Λ & Θ	pKG	p	0	p	0	m(G − 1)	−p	G(pK + m(m + 1)/2) + p − m
ν & Θ	same as Condition 8							same as baseline
T, Λ & ν	pK	p	0	pG	m(G − 1)	m(G − 1)	−p	G(p + m(m + 3)/2) + pK − 2m
T, Λ & Θ	pK	p	p(G − 1)	p	0	m(G − 1)	−p	G(p + m(m + 1)/2) + pK − m
T, ν & Θ	pK	pG	0	p	mG	0	−p	G(p + m(m + 1)/2) + pK
Λ, ν & Θ	same as loading and unique variance invariance
all four	pK	p	0	p	m(G − 1)	m(G − 1)	−p	Gm(m + 3)/2 + p(K + 1) − 2m

Table 4.

Parameter count for models with different identification conditions (K = 1). The structure is the same to Table 3.

	T	Λ	ν	diag(Θ)	κ	diag(Φ)	diag(Σ)	total
Total	pG	pG	pG	pG	mG	mG	0	G(4p + m(m + 3)/2)
Condition 7	pG	pG	0	pG	0	0	−pG
Condition 8	pG	pG	0	0	0	0	0	G(2p + m(m − 1)/2)
MYT	p	(p − m)G	0	pG	m(G − 1)	mG	−p − m(G − 1)
T	0	pG	pG	pG	0	0	−pG	same as baseline
Λ	pG	0	0	pG	0	0	0	same as baseline
ν or Θ	same as Condition 8							same as baseline
T & Λ	0	0	pG	pG	0	0	0	same as baseline
T & ν	same as MYT							same as baseline
T & Θ	p	pG	p(G − 1)	p	0	0	−p	same as baseline
Λ & ν	same as loading invariance							same as baseline
Λ & Θ	pG	p	0	p	0	m(G − 1)	−p	G(p + m(m + 1)/2) + p − m
ν & Θ	same as Condition 8							same as baseline
T, Λ & ν	p	p	0	pG	m(G − 1)	m(G − 1)	−p	G(p + m(m + 3)/2) + p − 2m
T, Λ & Θ	p	p	p(G − 1)	p	0	m(G − 1)	−p	G(p + m(m + 1)/2) + p − m
T, ν & Θ	p	pG	0	p	mG	0	−p	G(p + m(m + 1)/2) + p
Λ, ν & Θ	same as loading and unique variance invariance
all four	p	p	0	p	m(G − 1)	m(G − 1)	−p	Gm(m + 3)/2 + 2p − 2m

2.2. Factorial invariance

Establishing some degree of metric invariance in factor analytic models is an important step in comparing relationships between latent variables across samples, groups and other types of selection. While methods and terminology for metric invariance can vary across disciplines, most applications of metric invariance to structural equation modeling derive from the hierarchy of invariance levels first established by Meredith (1964a,b, 1993) and subsequently reviewed by Widaman and Reise (1997), Vandenberg and Lance (2000), Millsap and Meredith (2007) and Estabrook (2012). These levels of invariance create a hierarchy of constraints on parameters across groups that increasingly attributes group differences to the common factors. The four levels of factorial invariance most frequently referred to are: configural, weak, strong, and strict factorial invariance, each with varying restrictions on confirmatory factor models for continuous data.

Configural invariance is either the least stringent form of factorial invariance or a precondition for the Meredith definitions of invariance described elsewhere in this section. The only requirements of configural invariance are that there are the same number of factors in each group, and the pattern of salient (non-zero) and non-salient (zero) loadings is the same across groups. No restriction is imposed on the values of nonzero loadings.

The three levels of factorial invariance described by Meredith (1993) place additional constraints on a configurally invariant structure to establish metric invariance. Weak factorial invariance constrains the whole of the factor loading matrix to equality across groups, making all group differences in observed covariances attributable to differences in the factor covariance structure. This does not fit the definition of metric invariance: the free estimation of item intercepts in each group prevent the estimation of factor means and the testing of group differences in factor means.

Strong factorial invariance extends weak factorial invariance, further constraining item intercepts to equality across groups. Under strong factorial invariance, differences in observed means and covariances are due to group differences in factor means and covariances. Strict factorial invariance further constrains residual variances to equality, making all observed differences in means, variances and covariances attributable to the common factors. Both levels satisfy Meredith (1993) definition of metric invariance.

These definitions were all developed for continuous interval level responses. As such, all observed variables have an inherent scale and can be described as having means, variances and covariances with other variables. Ordinal and binary data lack these features, and thus alternative methods must be used. Millsap and Yun-Tein (2004) identified thresholds, factor loadings, intercepts and unique variances as parameters for studies of measurement invariance and obtained an identification condition for a model with configural invariance in both binary and polytomous data. Before reviewing these identification conditions in detail, we give a brief summary of the basic concepts in this area.

3. Identifying a Model

3.1. Identifiability and Identification Conditions

A statistical model is a family of distributions indexed by a set of parameters. If different sets of parameters index different members in this family of distribution, the model is identified or identifiable. Two statistical models are equivalent if they contain the same family of distributions. They are nested if one model is only a subset of the other model. For example, a exploratory factor analysis (EFA) model for normal data is a family of multivariate normal distributions² with a mean vector and a covariance matrix that satisfy Equation 1. This class of distribution is indexed by all parameters mentioned in the Introduction except the thresholds. This model is not identified because two sets of parameters that are related to each other by

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{\Lambda }}\hfill & =\hfill & \mathbf{\Lambda }\mathbf{U}\hfill \\ \stackrel{\sim }{\mathit{\nu }}\hfill & =\hfill & \mathit{\nu }+\mathbf{\Lambda }\mathit{\beta }\hfill \\ \stackrel{\sim }{\mathit{\kappa }}\hfill & =\hfill & {\mathbf{U}}^{-1}(\mathit{\kappa }-\mathit{\beta })\hfill \\ \stackrel{\sim }{\mathbf{\Phi }}\hfill & =\hfill & {\mathbf{U}}^{-1}\mathbf{\Phi }{{\mathbf{U}}^{-1}}^{\prime }\hfill \end{array}$$ (2)

produce exactly the same mean and covariance matrix for the multivariate normal distribution (i.e., they index the same member in the family of distributions) and fit data equally well. In this transformation, the p × p non-singular matrix U represents the rotational indeterminacy of the common factors and the indeterminacy of their variances, while the vector β of length m represents the indeterminacy of factor means. For a CFA model with a clustered loading structure and only non-negative loadings, U can only be a p × p positive diagonal matrix in order to preserve the structure of Λ̃. In this case, it represents the indeterminacy in the standard deviations of the common factors. The system of equations above defines a transformation that transforms one set of parameter into another without changing the model implied mean vector and covariance matrix. It represents all sources of non-identifiability of a model and can be used to examine whether a given set of constraints is an identification condition. A similar transformation for ordered categorical data will serve as an important tool in this paper.

To identify a model, constraints on parameters must be introduced. A set of constraints may or may not identify the model, and may or may not restrict the model to a smaller class of distributions. A set of constraints is called an identification condition, if it makes the model identifiable³ without restricting the class of distributions to a subset. By applying an identification condition, one obtains a statistically equivalent but identified model.

For any distribution in the model, one and only one set of parameters that satisfies a given identification condition can be found to index this distribution. As a result, an identification condition does not change the fit of the model. Instead, it merely chooses one of the many sets of parameters that fit the model equally well. For example,

$$\text{diag}(\mathbf{\Phi })=\mathbf{I}\text{and}\mathit{\kappa }=\mathbf{0}$$ (3)

are an identification condition for a CFA model for continuous outcomes with nonnegative loadings. This statement carries the following two-fold information: first, for any mean vector and covariance matrix that satisfy Equation 1, one may use Transformation 2 with $\mathbf{U}={\text{diag}}^{\frac{1}{2}}(\mathbf{\Phi })$ and β = κ to reparametrize this model to satisfy Identification Condition 3; second, for any mean vector and covariance matrix that satisfy both Equation 1 and Identification Condition 3, the parameter values are uniquely defined because the identification condition effectively fixes U and β in Transformation 2 to U = I and β = 0. Condition 3, however, is not an identification condition for an EFA model: imposing these constraints on both the left- and right-hand-side parameters of Transformation 2 only leads to β = 0 and diag[(UU′)⁻¹] = I, leaving the possibility of an oblique rotation. The two-fold information of an identification condition discussed above will serve as key reasoning in the proofs of propositions in this paper.

Identification conditions may not be unique, but different ways to identify the same model should end up with the same number of parameters, which is also the intrinsic dimension of the class of distributions. For example, instead of setting the common factor variance to 1, one may choose to set one loading of each common factor to 1 to identify the scale of that factor, though this option may lead to numerical instability if the chosen loading is close to 0.

3.2. Identifying a model for a single group

A CFA model for ordered categorical data has two types of latent variables: the m common factors and the p latent continuous responses for items. Neither has a fixed scale and both introduce indeterminacy of parameters into the model. To identify this model in a single group, we shall use the following transformation:

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & \mathit{\gamma }{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{-1}\mathbf{T}\hfill \\ \stackrel{\sim }{\mathbf{\Lambda }}\hfill & =\hfill & {\mathbf{\Delta }}^{-1}\mathbf{\Lambda }\mathbf{D}\hfill \\ \stackrel{\sim }{\mathit{\nu }}\hfill & =\hfill & {\mathbf{\Delta }}^{-1}\mathit{\nu }+{\mathbf{\Delta }}^{-1}\mathbf{\Lambda }\mathit{\beta }+\mathit{\gamma }\hfill \\ \stackrel{\sim }{\mathbf{\Theta }}\hfill & =\hfill & {\mathbf{\Delta }}^{-1}\mathbf{\Theta }{\mathbf{\Delta }}^{-1}\hfill \\ \stackrel{\sim }{\mathit{\kappa }}\hfill & =\hfill & {\mathbf{D}}^{-1}(\mathit{\kappa }-\mathit{\beta })\hfill \\ \stackrel{\sim }{\mathbf{\Phi }}\hfill & =\hfill & {\mathbf{D}}^{-1}\mathbf{\Phi }{\mathbf{D}}^{-1}\hfill \end{array}$$ (4)

where T = {τ_jk} is a p×K matrix that includes all finite thresholds. The m×m positive diagonal matrix D represents the indeterminacy of the common factor variances; the m×1 vector β represents the indeterminacy of the common factor means; the p × 1 vector γ and the p × p positive diagonal matrix Δ represent the indeterminacy of locations and scales of the latent continuous responses. The two positive diagonal matrices and the two vectors above can be freely chosen to transform one set of parameters into another set without changing the probabilities of response patterns. The total number of freely chosen transformation constants is 2(p + m), which is also the number of redundant parameters in the model. We have the following proposition:

Proposition 1

Two sets of parameters (T, Λ, υ, Θ, κ, Φ) and (T̃, Λ̃, υ̃, Θ̃, κ̃, Φ̃) are related to each other through Transformation 4 iff they produce the same probabilities of response patterns for the model in Section 2.1 with a clustered loading pattern and non-negative loadings.

Proof

We first prove the “only if” part. Suppose the two sets of parameters are related to each other through Transformation 4. It is straightforward to verify that the model-implied mean vector and covariance matrix of the latent continuous responses by the tilde parameters are (from Equation 1)

$$\stackrel{\sim }{\mathit{\mu }}={\mathbf{\Delta }}^{-1}\mathit{\mu }+\mathit{\gamma }\text{and}\mathbf{\sum }^{\sim }={\mathbf{\Delta }}^{-1}\mathbf{\sum }{\mathbf{\Delta }}^{-1}.$$

If we standardize the latent continuous responses, the thresholds become

$${\text{diag}}^{-\frac{1}{2}}(\mathbf{\sum }^{\sim })(\stackrel{\sim }{\mathbf{T}}-\stackrel{\sim }{\mathit{\mu }}{\mathbf{1}}^{\prime })={\text{diag}}^{-\frac{1}{2}}(\mathbf{\sum })\mathbf{\Delta }({\mathbf{\Delta }}^{-1}\mathbf{T}-{\mathbf{\Delta }}^{-1}\mathit{\mu }{\mathbf{1}}^{\prime })={\text{diag}}^{-\frac{1}{2}}(\mathbf{\sum })(\mathbf{T}-\mathit{\mu }{\mathbf{1}}^{\prime })$$

which are the same to the standardized thresholds in the original parameters. Because the two sets of parameters also imply the same correlations among the latent continuous responses (i.e. polychoric correlations), they produce the same probabilities of the response patterns.

Now we prove the “if” part. If two sets of parameters produce the same probabilities for the response patterns, they must produce the same multinomial probabilities for each item and therefore the same standardized thresholds. As a result, there must exist diagonal matrix Δ and vector γ such that

$$\stackrel{\sim }{\mathbf{T}}=\mathit{\gamma }{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{-1}\mathbf{T},\stackrel{\sim }{\mathit{\mu }}={\mathbf{\Delta }}^{-1}\mathit{\mu }+\mathit{\gamma }\text{and}\text{diag}(\mathbf{\sum }^{\sim })={\mathbf{\Delta }}^{-1}\text{diag}(\mathbf{\sum }){\mathbf{\Delta }}^{-1}.$$

Because the two sets of parameters must produce the same response probabilities for every pair of items, they must produce the same polychoric correlations, which strengthens the last equation above to Σ̃ = Δ⁻¹ΣΔ⁻¹. Using the expressions of mean and covariance structures in Equation 1, we have

$$\stackrel{\sim }{\mathit{\nu }}+\stackrel{\sim }{\mathbf{\Lambda }}\stackrel{\sim }{\mathit{\kappa }}={\mathbf{\Delta }}^{-1}\mathit{\nu }+{\mathbf{\Delta }}^{-1}\mathbf{\Lambda }\mathit{\kappa }+\mathit{\gamma }\text{and}$$ (5)

$$\stackrel{\sim }{\mathbf{\Lambda }}\stackrel{\sim }{\mathbf{\Phi }}{\stackrel{\sim }{\mathbf{\Lambda }}}^{\prime }+\stackrel{\sim }{\mathbf{\Theta }}={\mathbf{\Delta }}^{-1}\mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^{\prime }{\mathbf{\Delta }}^{-1}+{\mathbf{\Delta }}^{-1}\mathbf{\Theta }{\mathbf{\Delta }}^{-1}.$$ (6)

The two sides of Equation 6 gives two decompositions of the same covariance matrix into a diagonal matrix and a matrix of a given lower rank m < p. Because such decomposition is unique, we have Θ̃ = Δ⁻¹ΘΔ⁻¹ and Λ̃Φ̃Λ̃′ = Δ⁻¹ΛΦΛ′Δ⁻¹. The second equation implies that there must be a non-singular matrix D such that Λ̃ = Δ⁻¹ΛD and Φ̃ = D⁻¹ΦD⁻¹. Because both Λ̃ and Λ has the same clustered structure of non-negative loadings, D must be a positive diagonal matrix. Now Equation 5 becomes

$$\stackrel{\sim }{\mathit{\nu }}={\mathbf{\Delta }}^{-1}\mathit{\nu }+{\mathbf{\Delta }}^{-1}\mathbf{\Lambda }(\mathit{\kappa }-\mathbf{D}\stackrel{\sim }{\mathit{\kappa }})+\mathit{\gamma }$$

We denote the difference κ − Dκ̃ by β, and all equations in Transformation 4 have been proved.

For a model for categorical outcomes, non-identifiablity arises when two sets of parameters imply the same set of probabilities of response patterns. Transformation 4 links such two sets of parameters with two diagonal matrices D and Δ and two vectors β and γ, which explain the mechanism of such non-identifiability. To identify a model for a single group, 2(p + m) constraints must be introduced to remove the indeterminacy of parameters without restricting the model.

For example, one widely used identification condition (e.g., Christoffersson, 1975) is

$$\text{diag}(\mathbf{\Phi })=\mathbf{I},\mathit{\kappa }=\mathbf{0},\mathit{\nu }=\mathbf{0},\text{and}\text{diag}(\mathbf{\sum })=\mathbf{I}.$$ (7)

The first equation sets D = I in Transformation 4 (because diag(Φ̃) = diag(Φ) = I implies D = I); the second equation sets β = 0; the third equation sets γ = 0. Note the last equation defines p constraints on the variances of the latent responses, which are functions of the unique variances, factor loadings and factor variances. This sets Δ = I in the Transformation 4. It can also be verified that any set of parameters can be transformed to satisfy Condition 7 using Transformation 4 with properly chosen D, Δ, β and γ. An alternative identification condition constrains the variances of the residuals rather than the latent responses:

$$\text{diag}(\mathbf{\Phi })=\mathbf{I},\mathit{\kappa }=\mathbf{0},\mathit{\nu }=\mathbf{0},\text{and}\mathbf{\Theta }=\mathbf{I}.$$ (8)

Both of these options identify the model, but the θ-parametrization of Condition 8 may give numerical instability if one of the unique variances is close to 0. Similar to models for continuous outcomes, in both Conditions 7 and 8 one may fix a reference loading of a factor rather than the factor variance.

3.3. Identifying a model with configural invariance

A model with configural invariance is the starting point of invariance study. In this paper we call it a baseline model. To identify this model, one may identify each group separately with Condition 7 or Condition 8. Alternatively, one may first identify one group and then identify the remaining groups through equality constraints across groups. The identification condition proposed by Millsap and Yun-Tein (2004, p. 485) for polytomous data is given below⁴.

1. For all groups set ν^(g) = 0 and a reference loading to 1 for each factor;

2. In the first group set κ⁽¹⁾ = 0 and diag(Σ⁽¹⁾) = I;

3. Set invariant one threshold per item and a second threshold in the reference item of each factor.

The total number of parameters in this model is G(pK +p+m(m−1)/2), the same number as we use Condition 7 or 8 for each group. We refer to this parametrization (identification condition) of the baseline model as MYT parametrization (identification condition).

When data are dichotomous, imposing invariance on a second threshold is impossible. In this case, the latent response variance is set to 1 for the reference items. Parameter counts of the three different ways to identify this model are listed in the second block of Tables 3 and 4 for polytomous and binary outcomes.

4. Identifying models of different invariance levels

To test invariance, models with different invariant parameters can be compared. The issue of model comparison will not be discussed in this paper; instead, we focus on the identification conditions for models with different invariance properties. We limit our attentions to the invariance of the four measurement parameters: thresholds, factor loadings, intercepts and unique variances (Millsap and Yun-Tein, 2004, pp.483–484).

The intuitive way of building a model with parameter invariance is to impose invariance constraints on an identified baseline model. For example, a model with factor loading invariance can be built by constraining the loadings to be invariant cross groups in the baseline model identified by MYT parametrization (Millsap and Yun-Tein, 2004, p.494). Unfortunately, this approach has its drawbacks, as explained below.

An identification condition of the baseline model defines the scale of each latent continuous response and provides each with a mean and a variance for subsequent analyses. Because the estimates of the measurement parameters depend on these scales, constraints on these parameters across groups can have wildly different results depending on which identification condition is used in the baseline model.

This problem can be explained with a brief illustration whose parameters and results are presented in Tables 1 and 2. Consider a test of invariance involving one common factor each measured on four variables in two groups. The true values as listed in the first column of Table 1 have invariant thresholds, factor loadings and intercepts, but residual variances vary across groups. In the first group the latent continuous responses have unit variance but in the second group this is true only for the second item. We obtain a sample of size 10⁴ in each group with these true values for use in this illustration.

Table 1.

Parameter estimates of a two-group model for four binary items of one factor identified in different ways.

	True Value		δ-1		MYT		1 MYT 2
	G 1	G 2	G 1	G 2	G 1	G 2	G 1	G 2
	0.8		0.8*		0.8*		0.80	0.83
Loadings	0.8		0.80	0.72	0.80	2.47	0.8*
	0.8		0.78	0.68	0.78	0.33	0.78	0.83
	0.8		0.78	0.64	0.78	0.48	0.79	0.85
Intercepts	0		0*		0*		0*
	0.36	0.18	***		***	***	***	0.19
Unique	0.36	0.36				6.41		***
Variances	0.36	0.54				0.16		0.51
	0.36	0.72				0.44		0.70
Thresholds	−.75		−.76	−.83	−.76		−.76
	−.25		−.25	−.25	−.25		−.25
	0.25		0.25	0.24	0.25		0.25
	0.75		0.75	0.64	0.75		0.75
Factor M.	0		0*		0*	0.32	0*	−.01
Factor Var.	1		1.03	1.21	1.03	1.80	1.02	0.93

^*fixed value;

^***fixed at one less the communality of that item.

Table 2.

Fit statistics for the models in Table 1. The configural invariance model corresponds to the models and parameter estimates presented in Table 1. Models with weak factorial invariance further constrain factor loadings to invariance across groups, yielding 3 more degrees of freedom.

	Identification	Model Fit
Invariance	Method	−2lnL	Δχ2	Δdf	p
Configural	All three	84592.24
	δ-1	84646.36	54.11	3	<.001
Weak	MYT-1	84627.39	35.15	3	<.001
	MYT-2	84593.66	1.41	3	.70

Table 1 shows parameter estimates in the baseline model identified in different ways: estimates in Column 2 are produced with each group identified by Condition 7, but instead of fixing the factor variance, the first loading is set to 0.8; estimates in Columns 3 and 4 are produced with MYT parametrization with the first or second loading set to 0.8. These estimates were estimated with maximum likelihood using OpenMx (Boker, Neale, Maes et. al., 2011; Neale, Hunter, Pritkin et. al., 2015) in R (R Development Core Team, 2013). These identification conditions constrain the scale of each latent variable, and thus the residual variances, in different ways. As the true parameters do not imply unit variances for the latent responses in the second group (except for the second item), the first two identification methods effectively rescale the underlying continuous responses, which in turn transforms the factor loadings or thresholds, leading to pronounced differences in their estimates despite their invariance in the true values. The third identification condition is satisfied in the true parameters and therefore its use only leads to minor discrepancies in the loadings between the two groups during to sampling error. Despite the different parameter estimates, all three identification methods produce the same likelihood value as shown in Table 2.

Now we construct models with loadings invariance by imposing constraints on loadings across groups in the three versions of the baseline model. Because of the different sizes of group differences in the loading estimates of the baseline models, models with loading invariance find different levels of loss of fit as shown in the second half of Table 2. The first two methods find larger deficits in fit, leading to the rejection of loading invariance. The third method has smaller loss of fit and fails to reject loading invariance. Although the three models with loading invariance are intended as different parameterizations of the same model, they resulted in different maximum likelihood value, suggesting that they are not equivalent to each other. As we will see later, none of these three models is equivalent to a model with only loading invariance because such model should be equivalent to the baseline model.

This scaling problem can be equivalently stated using Transformation 4. An identification condition transforms true parameters that may not satisfy it into a new set of parameters that satisfies it. The loadings (Λ̃) under a specific identification condition can be expressed as the product of the true loadings (Λ) and two scaling matrices (Δ and D) that depend on the identification condition. Even though the true loadings are invariant across groups, different scaling matrices may arise for different groups and result in non-invariant loadings in the identified model.

As we have seen above, imposing invariance constraints on loadings in a baseline model identified in different ways may lead to statistically non-equivalent models. Mathematically, this problem arises because the identification condition used in the baseline model may become restrictive when additional invariance conditions are introduced. They restrict the model with loading invariance in different ways, so the resultant models differ. Such restrictions change the model and the model is no longer “just” loading invariant.

To resolve this problem, we advocate a different approach that does not start with an identified baseline model. Instead, we identify models with different levels of invariance on a case by case basis. The model with only the desired invariance properties is first considered, and then appropriate constraints are added to “just” identify this model without imposing restrictions. Below we give the identification conditions for these models. Parameter counts of the models with the identification conditions are listed in Tables 3 and 4 for polytomous and binary data respectively. Surprisingly, we found that for some parameters such as factor loadings, its invariance cannot be tested alone: a model with only invariant loadings is equivalent to the baseline model.

5. Identification conditions of models of different invariance levels

It is well known that a model with full measurement invariance can be identified with the following condition:

$$\mathit{\nu }=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},{\mathit{\kappa }}^{(1)}=\mathbf{0}\text{and}\text{diag}({\mathbf{\Phi }}^{(1)})=\mathbf{I}$$ (9)

In Sections 5.1 through 5.7, we consider the various situations where only some but not all of these four types of parameters are invariant and provide proofs of their identification conditions. Section 5.1 covers threshold invariance. Section 5.2 describes which types of invariance are testable or untestable by themselves. Sections 5.3 through 5.5 cover invariance of thresholds and one other parameter type. Section 5.6 covers invariance of loadings and unique variances. Section 5.7 describes remaining cases where three of the four types of parameters are invariant. Section 5.8 briefly discusses the possibility of testing factor means and variances under models with different levels of invariance.

Please note that the proofs of all propositions below follow the same logic: to establish a set of constraints as an identification condition, we need to prove: (a) this condition does not restrict the model, and (b) with this condition the model is identified. For (a), we prove that any set of parameters of this model can be transformed to satisfy this condition without changing the probabilities of response patterns, which can be done by properly choosing the matrices D and Δ and the vectors β and γ for each group in Transformation 4. For (b), we prove that if this condition is satisfied by both the tilde and regular parameters in Transformation 4, we can reduce D and Δ to an identity matrix and β and γ to a null vector. This general logical framework will not be repeated in each proof.

5.1. Invariance of thresholds

We first consider the case of threshold invariance. For binary (K = 1) or ternary (K = 2) outcomes, a linear transformation on the latent response variable $y_j^{\ast }$ in one group can match its thresholds to those of another group. As a result, any set of parameters with configural invariance can be transformed to satisfy threshold invariance through Transformation 4. This is summarized in the following propositions. Note that in all propositions below “model” refers to a CFA model with a clustered factor structure of nonnegative loadings.

Proposition 2

The following constraints are an identification condition to a baseline model for ordered ternary data:

$${\mathit{\nu }}^{(1)}=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\mathit{and}\mathit{for}\mathit{all}g:{\mathbf{T}}^{(g)}={\mathbf{T}}^{(1)},{\mathit{\kappa }}^{(g)}=\mathbf{0}\mathit{and}\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}$$ (10)

Proof

For ternary items in multiple groups, Transformation 4 becomes

$$\{\begin{array}{lll}{\stackrel{\sim }{\mathbf{T}}}^{(g)}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}{\mathbf{T}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Lambda }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Theta }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Theta }}^{(g)}{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (11)

We first prove that Condition 10 does not restrict the model. We first choose β^(g) = κ^(g), ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(g)}),{\mathbf{\Delta }}^{(1)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and γ⁽¹⁾ = −Δ⁽¹⁾⁻¹ν⁽¹⁾ − Δ⁽¹⁾⁻¹Λ⁽¹⁾β⁽¹⁾ and the transformation above can transform any set of parameters to satisfy all equations in Condition 10 except T^(g) = T⁽¹⁾. Now we need to choose Δ^(g) and γ^(g) for g = 2, ···, G so that for all the G − 1 groups

$${\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}{\mathbf{T}}^{(g)}={\stackrel{\sim }{\mathbf{T}}}^{(1)}$$ (12)

holds, where T̃⁽¹⁾ = γ⁽¹⁾1′ +Δ⁽¹⁾⁻¹T⁽¹⁾ is already determined by our choice of γ⁽¹⁾ and Δ⁽¹⁾ above. For each g, Equation 12 is a system of p × 2 linear equations of 2p unknowns. In particular, its ith row comprises of the following system of equations:

$${\gamma }_i^{(g)}+{\delta }_{ii}^{(g)-1}{\tau }_{i1}^{(g)}={\stackrel{\sim }{\tau }}_{i1}^{(1)}\text{and}{\gamma }_i^{(g)}+{\delta }_{ii}^{(g)-1}{\tau }_{i2}^{(g)}={\stackrel{\sim }{\tau }}_{i2}^{(1)}$$

which has a unique solution of ${\gamma }_i^{(g)}$ and ${\delta }_{ii}^{(g)}$ because ${\tau }_{i1}^{(g)}<{\tau }_{i2}^{(g)}$.

Now we prove that Condition 10 identifies the model. If this condition is satisfied by on both sides of Transformation 11: the last equation of Transformation 11 along with diag(Φ^(g)) = diag(Φ̃ ^(g)) = I implies D^(g) = I; the fifth equation of Transformation 11 along with κ^(g) = κ̃ ^(g) = 0 implies β^(g) = 0; the constraint diag(Σ⁽¹⁾) = diag(Σ̃⁽¹⁾) = I implies Δ⁽¹⁾ = I; the third equation of Transformation 11, which now becomes ν̃^(g) = Δ^(g)−1ν^(g) + γ^(g) along with ν⁽¹⁾ = ν̃ ⁽¹⁾ = 0 implies γ⁽¹⁾ = 0. Now the first equation of Transformation 11 for g = 1 becomes T̃⁽¹⁾ = T⁽¹⁾. If the equations T^(g) = T⁽¹⁾ (Condition 10) and T̃^(g) = T̃⁽¹⁾ hold for g = 2, 3, ···, G, we must have T̃^(g) = T^(g) for g = 2, 3, ···, G, which leads to the system of Equations

$${\gamma }_i^{(g)}+{\delta }_{ii}^{(g)-1}{\tau }_{i1}^{(g)}={\tau }_{i1}^{(g)}\text{and}{\gamma }_i^{(g)}+{\delta }_{ii}^{(g)-1}{\tau }_{i2}^{(g)}={\tau }_{i2}^{(g)}$$

for g = 2, 3, ···, G and i = 1, 2, ···, p. This implies γ^(g) = 0 and Δ^(g) = I. Now all four sources of non-identifiability in Transformation 11 are fixed.

Proposition 3

The following constraints are an identification condition for a baseline model for binary data:

$$\mathit{For}\mathit{all}g:{\mathit{\tau }}^{(g)}=\mathbf{0},{\mathit{\kappa }}^{(g)}=\mathbf{0},\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I},\mathit{and}\text{diag}({\mathbf{\sum }}^{(g)})=\mathbf{I}.$$ (13)

Proof

For binary items, Transformation 11 becomes

$$\{\begin{array}{lll}{\stackrel{\sim }{\mathit{\tau }}}^{(g)}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}{\mathit{\tau }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Lambda }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Theta }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Theta }}^{(g)}{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (14)

Note that τ̃ ^(g) and τ ^(g) are now vectors.

First, if we choose β^(g) = κ^(g), ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(g)}),{\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(g)})$ and γ^(g) = −Δ^(g)−1τ ^(g) in the transformation then any set of parameters can be transformed to satisfy Constraints 13.

Second, we prove that if both sides of Transformation 14 satisfy Constraints 13, then β^(g) = 0, D^(g) = I, Δ^(g) = I and γ^(g) = 0. In fact, setting diag(Φ̃^(g)) = diag(Φ^(g)) = I in the last equation of Transformation 14 gives D^(g) = I, setting κ̃ ^(g) = κ^(g) = 0 in the penultimate equation of Transformation 14 gives β^(g) = 0, setting diag(Σ̃^(g)) = diag(Σ^(g)) = I gives Δ^(g) = I and setting τ̃ ^(g) = τ ^(g) = 0 in the first equation of Transformation 14 gives γ^(g) = 0.

The propositions above indicate that for binary and ternary items, threshold invariance cannot be tested alone because they can be automatically satisfied. In other words, a model with invariant thresholds is statistically equivalent to a configural invariant model. When there are three or more thresholds for each item, a linear transformation that matches those thresholds across groups generally does not exist, so threshold invariance becomes testable. To identify a model with threshold invariance, the following identification condition can be used:

$${\mathit{\nu }}^{(1)}=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\text{and}\text{for}\text{all}g:{\mathit{\kappa }}^{(g)}=\mathbf{0}\text{and}\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}$$ (15)

Intuitively, the first group is identified because it uses parameterization specified by Condition 7. For the remaining groups the scale of their latent continuous responses are identified through invariant thresholds; the scale of common factors are identified by fixing the factor variances and means as in a model with observed continuous responses. Note that Condition 15 also identifies a model with threshold invariance for ordered ternary items (K = 2). The total number of parameters is p(K−2)+G(3p+m(m−1)/2), which coincide with that of the baseline model for K = 2. Formally we have the following proposition.

Proposition 4

Condition 15 is an identification condition for a model with more than one thresholds and threshold invariance.

Proof

For a multi-group model with threshold invariance, Transformation 4 becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ {\stackrel{\sim }{\mathbf{\Lambda }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Theta }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Theta }}^{(g)}{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (16)

Note that the matrices of thresholds T and T̃ do not bear a superscript.

First, any set of parameters with invariant thresholds can be transformed to satisfy Condition 15 using the transformation above with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(g)})$, β^(g) = κ^(g), ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and γ^(g) = −Δ⁽¹⁾⁻¹(ν⁽¹⁾ + Λ⁽¹⁾κ⁽¹⁾). Note that Δ^(g) and γ^(g) do not differ across groups, so the transformed threshold matrix T̃ is still invariant across groups. This shows that Condition 15 does not restrict the model.

Second, by applying Condition 15 to parameters on both sides of Transformation 16, we can easily obtain D^(g) = I, β^(g) = 0, γ⁽¹⁾ = 0 and Δ⁽¹⁾ = I. Now we only need to extend the last two equalities to the remaining G−1 groups. Note that the first equation in Transformation 16 defines, for each item j, G linear functions with coefficients ${\gamma }_j^{(g)}$ and ${\delta }_{jj}^{(g)}$ that map the K thresholds on the jth row of T onto the K thresholds on the jth row of T̃. Because both T and T̃ do not vary across groups, the G linear functions share K > 1 common points, so the G linear functions must be identical, with γ^(g) = γ⁽¹⁾ = 0 and Δ^(g) = Δ⁽¹⁾ = I. Now all four sources of indeterminacy are removed, so Condition 15 is able to identify the model.

5.2. Types of invariance that are not testable

A baseline model with Identification Condition 8 for each group automatically satisfies the invariance of unique variances and that of intercepts. As a result, invariance of either or both intercepts and unique variances cannot be tested alone.

We further have the following proposition.

Proposition 5

The following constraints are an identification condition for a baseline model:

$$\mathit{For}\mathit{all}g:\mathit{the}\mathit{nonzero}\mathit{loadings}of{\mathbf{\Lambda }}^{(g)}be\mathit{1},{\mathit{\kappa }}^{(g)}=\mathbf{0},{\mathit{\nu }}^{(g)}=\mathbf{0}\mathit{and}\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}$$ (17)

Proof

First, Condition 17 does not restrict the model. In fact, in Transformation 11 we can choose Δ^(g) to be a diagonal matrix of factor loadings of the items, and choose ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}{\mathbf{\Phi }}^{(g)}$, β^(g) = κ^(g) and γ^(g) = −Δ^(g)−1(ν^(g) + Λ^(g)κ^(g)). The transformed parameters satisfy Condition 17.

Second, if this condition is satisfied by parameters on both sides of Transformation 11, we immediately have β^(g) = 0, D^(g) = I, γ^(g) = −Δ^(g)−1Λ^(g)β^(g) = 0. Now the second equation of Transformation 11 becomes Λ̃^(g) = Δ^(g)−1Λ^(g). Because the loading matrices on both sides are the same binary matrix, we have Δ^(g) = I.

Because a baseline model with the identification condition above automatically satisfies the invariance of loadings and intercepts, the invariance of either or both loadings and intercepts cannot be tested alone.

For four or more categories, there are a total of five models equivalent to the baseline model as discussed above. For three categories, the model with threshold invariance is also equivalent to the baseline model as discussed in the last subsection. For binary data, three more models (invariance of thresholds and loadings, of thresholds and intercepts, and of thresholds and unique variances) are equivalent to the baseline model. They are discussed in their respective subsections below.

5.3. Invariance of thresholds and loadings

For dichotomous data (i.e. K = 1), a model with both invariant thresholds and invariant loadings is statistically equivalent to the baseline model. In fact, we have the following proposition.

Proposition 6

The constraints below are an identification condition for a baseline model for binary data:

$$\mathit{For}\mathit{all}g:\mathit{the}\mathit{nonzero}\mathit{loadings}of{\mathbf{\Lambda }}^{(g)}be\mathit{1},{\mathit{\kappa }}^{(g)}=\mathbf{0},{\mathit{\tau }}^{(g)}=\mathbf{0}\mathit{and}\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}$$ (18)

Proof

First, Condition 18 is not restrictions. In fact, in Transformation 14 if we choose Δ^(g) to be a diagonal matrix of factor loadings of the items and choose ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}{\mathbf{\Phi }}^{(g)}$, β^(g) = κ^(g) and γ^(g) = −Δ^(g)−1τ ^(g), the transformed set of parameters satisfy Condition 18.

Second, Condition 18 identifies the model. In fact, if it is satisfied by parameters on both sides of Transformation 14, it is straightforward to obtain β^(g) = 0, D^(g) = I, γ^(g) = 0 and Δ^(g) = I.

The proposition above shows that the baseline model for binary data is equivalent to a model with threshold and loading invariance, so such invariance cannot be tested alone.

If there are more than two categories, a model with threshold and loading invariance is more restrictive than the baseline model and can therefore be tested.

Proposition 7

The following is an identification condition for a model with threshold and loading invariance for three or more ordered categories:

$$\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},{\mathit{\nu }}^{(1)}=\mathbf{0},\text{diag}({\mathbf{\Phi }}^{(1)})=\mathbf{I},\mathit{and}\mathit{for}\mathit{all}g:{\mathit{\kappa }}^{(g)}=\mathbf{0}.$$ (19)

Proof

Transformation 11 now becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ \stackrel{\sim }{\mathbf{\Lambda }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Theta }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Theta }}^{(g)}{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (20)

Note that both thresholds and loadings do not bear a superscript.

First, any set of parameters with invariant thresholds and loadings can be transformed to satisfy Condition 19 using this Transformation with ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$, γ^(g) = −Δ⁽¹⁾⁻¹(ν⁽¹⁾ + Λκ⁽¹⁾), β^(g) = κ^(g) and ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(1)})$. Note that Δ^(g), D^(g) and γ^(g) are only related to parameters in the first group and are therefore invariant across groups, so that the resultant transformed loadings and thresholds can be invariant cross groups.

Second, if Condition 19 is satisfied on both sides of Transformation 20, we immediately have β^(g) = 0, D⁽¹⁾ = I, Δ⁽¹⁾ = I and γ⁽¹⁾ = 0. Now we need to extend the last three equalities to the remaining G − 1 groups. Similar to the reasoning in the proof of Proposition 4, the first equation of Transformation 20 implies γ^(g) = γ⁽¹⁾ = 0 and Δ^(g) = Δ⁽¹⁾ = I. The second equation of Transformation 20 now implies D^(g) = D⁽¹⁾ = I.

5.4. Invariance of thresholds and intercepts

Now we consider threshold and intercept invariance. We have the following proposition

Proposition 8

An identification condition for a model with invariant thresholds and intercepts for three or more ordered categories is given by

$$\mathit{\nu }=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\mathit{and}\mathit{for}\mathit{all}g:\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}.$$ (21)

Proof

For a multi-group model with threshold and intercept invariance, Transformation 11 becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ {\stackrel{\sim }{\mathbf{\Lambda }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathbf{D}}^{(g)}\hfill \\ \stackrel{\sim }{\mathit{\nu }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathit{\nu }+{\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Theta }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Theta }}^{(g)}{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (22)

Again, invariant parameters do not have a superscript. First, any set of parameters with invariant thresholds and intercepts can be transformed to satisfy Condition 21 using Transformation 22 with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(g)})$, β^(g) = 0, ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$and ${\mathit{\gamma }}^{(g)}=-{\text{diag}}^{-\frac{1}{2}}({\mathbf{\sum }}^{(1)})\mathit{\nu }$.

We then show that Condition 21 identifies the parameters. If this condition is satisfied on both sides of Transformation 22, we immediately have D^(g) = I and Δ⁽¹⁾ = I. Similar to the reasoning in the proof of Proposition 4, the first equation of Transformation 20 implies γ^(g) = γ⁽¹⁾ (denoted by γ below) and Δ^(g) = Δ⁽¹⁾ = I. Because ν = ν̃ = 0, we must have γ = −Λ^(g)β^(g). For the general case where loadings on the same factor are not proportional across groups, we must have β = 0 and γ = 0. Now all four sources of indeterminacy in the transformation have been fixed.

It should be noted that technically Identification Condition 21 cannot identify the model if, after imposing this condition, loadings on the same factor are proportional across groups. Because this singularity occurs on a subset of the parameter space of lower dimensions, it does not affect the practical use of Condition 21.

For dichotomous items (K = 1), a model with threshold and intercept invariance is equivalent to the baseline model. In fact, the MYT parametrization of a baseline model automatically satisfies these invariance relations.

5.5. Invariance of thresholds and unique variances

Proposition 9

The following constraints are an identification condition for a model with invariant thresholds and unique variances:

$${\mathit{\nu }}^{(1)}=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I}\mathit{and}\mathit{for}\mathit{all}g:{\mathit{\kappa }}^{(g)}=\mathbf{0}\mathit{and}\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}$$ (23)

Proof

For the current situation Transformation 11 becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ {\stackrel{\sim }{\mathbf{\Lambda }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ \stackrel{\sim }{\mathbf{\Theta }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Theta }{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (24)

First, any set of parameters with invariant thresholds and unique variances can be transformed to satisfy Condition 23 using Transformation 24 with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(g)})$, β^(g) = κ^(g), ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and ${\mathit{\gamma }}^{(g)}=-{\text{diag}}^{-\frac{1}{2}}({\mathbf{\sum }}^{(1)})({\mathit{\nu }}^{(1)}+{\mathbf{\Lambda }}^{(1)}{\mathit{\beta }}^{(1)})$. Second, if Condition 23 is satisfied on both sides of Transformation 24, we immediately have D^(g) = I, β^(g) = 0, Δ⁽¹⁾ = I and γ⁽¹⁾ = 0. Now the first and fourth equation of Transformation 24 implies Δ^(g) = Δ⁽¹⁾ = I and γ^(g) = γ⁽¹⁾ = 0.

As a special case, the Identification Condition 23 also applies to dichotomous items, but in this case the model is statistical equivalent to the baseline model. This can be easily verified by calculating the effective number of parameters.

5.6. Invariance of loadings and unique variances

Proposition 10

The following constraints are an identification condition for a model with invariant loadings and unique variances:

$$\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\text{diag}({\mathbf{\Phi }}^{(1)})=\mathbf{I},\mathit{and}\mathit{for}\mathit{all}g:{\mathit{\kappa }}^{(g)}=\mathbf{0}\mathit{and}{\mathit{\nu }}^{(g)}=\mathbf{0}.$$ (25)

Proof

Transformation 11 now becomes

$$\{\begin{array}{lll}{\stackrel{\sim }{\mathbf{T}}}^{(g)}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}{\mathbf{T}}^{(g)}\hfill \\ \stackrel{\sim }{\mathbf{\Lambda }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ \stackrel{\sim }{\mathbf{\Theta }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Theta }{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (26)

First, any set of parameters with invariant loadings and unique variances can be transformed to satisfy Condition 25 using Transformation 26 with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(1)})$, β^(g) = κ^(g), ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and γ^(g) = −Δ⁽¹⁾⁻¹(ν^(g) + Λκ^(g)). Second, if Condition 25 is satisfied on both sides of Transformation 26, we immediately have D⁽¹⁾ = I, β^(g) = 0, Δ⁽¹⁾ = I and γ^(g) = 0. The second and fourth equations of Transformation 24 further implies Δ^(g) = Δ⁽¹⁾ = I and D^(g) = D⁽¹⁾ = I.

5.7. Invariance of three types of parameters

Because Identification Condition 25 for a model with invariant loadings and unique variances sets the intercepts to 0, this model is statistically equivalent to a model with invariant loadings, intercepts and unique variances. In the propositions below we discuss the remaining cases where three types of parameters are invariant.

Proposition 11

The following is an identification condition for a model with invariant thresholds, loadings and intercepts:

$$\mathit{\nu }=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\text{diag}({\mathbf{\Phi }}^{(1)})=\mathbf{I}\mathit{and}{\mathit{\kappa }}^{(1)}=\mathbf{0}$$ (27)

Proof

Transformation 11 now becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ \stackrel{\sim }{\mathbf{\Lambda }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathbf{D}}^{(g)}\hfill \\ \stackrel{\sim }{\mathit{\nu }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathit{\nu }+{\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ {\stackrel{\sim }{\mathbf{\Theta }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Theta }}^{(g)}{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (28)

First, any set of parameters with invariant thresholds, loadings and intercepts can be transformed to satisfy Condition 27 using Transformation 28 with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(1)})$, β^(g) = κ⁽¹⁾, ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and ${\mathit{\gamma }}^{(g)}=-{\text{diag}}^{-\frac{1}{2}}({\mathbf{\sum }}^{(1)})(\mathit{\nu }+\mathbf{\Lambda }{\mathit{\kappa }}^{(1)})$.

Second, if condition holds on both sides of Transformation 28, we have D⁽¹⁾ = I, Δ⁽¹⁾ = I, β⁽¹⁾ = 0 and γ⁽¹⁾ = 0. Now we need to extend these equalities to the remaining G − 1 groups, for which we need to consider the cases of binary and polytomous data separately below.

If there are more than one thresholds, similar to the reasoning in the proof of Proposition 4, the first equation of Transformation 28 implies Δ^(g) = Δ⁽¹⁾ = I and γ^(g) = γ⁽¹⁾ = 0. Now the second and third equations in Transformation 28 implies D^(g) = D⁽¹⁾ = I and β^(g) = 0.

For binary data, the second equation in Transformation 28 implies that Δ^(g) must take the following structure: ${\delta }_{jj}^{(g)}=c_j{d}_{l(j)l(j)}^{(g)}$, where l(j) refers to the index of the factor on which the jth item loads. Because Δ⁽¹⁾ = I and D⁽¹⁾ = I, we must have c_j = 1. Because ν̃ = ν = 0, we have γ^(g) = −Δ^(g)−1Λβ^(g). Because γ⁽¹⁾ = 0 and Δ⁽¹⁾ = I, we have τ̃ = τ. (Remember for binary items T becomes a vector τ.) Now the first equation of Equation 28 becomes τ = −Δ^(g)−1Λβ^(g)+Δ^(g)−1τ, or equivalently (I−Δ^(g))τ = Λβ^(g). The jth row of this equation is $(1-{\delta }_{jj}^{(g)}){\tau }_j={\lambda }_{jl(j)}{\beta }_{l(j)}^{(g)}$. Because we have proved ${\delta }_{jj}^{(g)}=d_{l(j)l(j)}^{(g)}$, this equation becomes $(1-d_{l(j)l(j)}^{(g)}){\tau }_j/{\lambda }_{jl(j)}={\beta }_{l(j)}^{(g)}$. Note that in general the ratio τ_j/λ_jl(j) varies with j but $1-d_{l(j)l(j)}^{(g)}$ and ${\beta }_{l(j)}^{(g)}$ stay the same for items on the same factor, so we must have D^(g) = I and β^(g) = 0, which further implies Δ^(g) = I and γ^(g) = 0. Now all four sources of indeterminacy of parameters are fixed, so the model is identified.

It should be noted that for binary data, Identification Condition 27 is not able to identify the model if, after imposing this condition, the ratios of correspondent thresholds and loadings are the same for all items of a given factor. Because this singularity occurs on a lower dimensional subset of the parameter space, it does not affect the practical use of this identification condition.

Proposition 12

Below is an identification condition for a model with invariant thresholds, loadings and unique variances:

$${\nu }^{(1)}=0,\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\text{diag}({\mathbf{\Phi }}^{(1)})=\mathbf{I},\mathit{and}\mathit{for}\mathit{all}g:{\mathit{\kappa }}^{(g)}=\mathbf{0}$$ (29)

Proof

For our current situation, Transformation 11 becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ \stackrel{\sim }{\mathbf{\Lambda }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathbf{D}}^{(g)}\hfill \\ {\stackrel{\sim }{\mathit{\nu }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathit{\nu }}^{(g)}+{\mathbf{\Delta }}^{(g)-1}\mathbf{\Lambda }{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ \stackrel{\sim }{\mathbf{\Theta }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Theta }{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (30)

This identification condition does not restrict the model because any set of parameters with invariant thresholds, loadings and unique variances can be transformed to satisfy Condition 29 using Transformation 30 with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(1)})$, β^(g) = κ^(g), ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and ${\mathit{\gamma }}^{(g)}=-{\text{diag}}^{-\frac{1}{2}}({\mathbf{\sum }}^{(1)})({\mathit{\nu }}^{(1)}+\mathbf{\Lambda }{\mathit{\kappa }}^{(1)})$. Condition 29 removes all indeterminacy of parameters. In fact, if this condition holds in both sides of Transformation 30, we immediately have β^(g) = 0, Δ⁽¹⁾ = I, D⁽¹⁾ = I and γ⁽¹⁾ = 0. The fourth equation of Transformation 30 implies Δ^(g) = Δ⁽¹⁾ = I; the first and second equations of Transformation 30 now imply γ^(g) = γ⁽¹⁾ = 0 and D^(g) = D⁽¹⁾ = I.

Identification Condition 29 applies to both binary and ordered polytomous data, but for binary data, the model is statistically equivalent to one with only invariant loadings and unique variances. This can be verified by checking the effective number of parameters of both models.

Proposition 13

Below is an identification condition for a model with invariant thresholds, intercepts and unique variances:

$$\mathit{\nu }=\mathbf{0},\text{diag}({\mathbf{\sum }}^{(1)})=\mathbf{I},\mathit{and}\mathit{for}\mathit{all}g\text{diag}({\mathbf{\Phi }}^{(g)})=\mathbf{I}$$ (31)

Proof

For our current situation, Transformation 11 becomes

$$\{\begin{array}{lll}\stackrel{\sim }{\mathbf{T}}\hfill & =\hfill & {\mathit{\gamma }}^{(g)}{\mathbf{1}}^{\prime }+{\mathbf{\Delta }}^{(g)-1}\mathbf{T}\hfill \\ {\stackrel{\sim }{\mathbf{\Lambda }}}^{(g)}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathbf{D}}^{(g)}\hfill \\ \stackrel{\sim }{\mathit{\nu }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathit{\nu }+{\mathbf{\Delta }}^{(g)-1}{\mathbf{\Lambda }}^{(g)}{\mathit{\beta }}^{(g)}+{\mathit{\gamma }}^{(g)}\hfill \\ \stackrel{\sim }{\mathbf{\Theta }}\hfill & =\hfill & {\mathbf{\Delta }}^{(g)-1}\mathbf{\Theta }{\mathbf{\Delta }}^{(g)-1}\hfill \\ {\stackrel{\sim }{\mathit{\kappa }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}({\mathit{\kappa }}^{(g)}-{\mathit{\beta }}^{(g)})\hfill \\ {\stackrel{\sim }{\mathbf{\Phi }}}^{(g)}\hfill & =\hfill & {\mathbf{D}}^{(g)-1}{\mathbf{\Phi }}^{(g)}{\mathbf{D}}^{(g)-1}\hfill \end{array}$$ (32)

Condition 31 does not restrict the model because any set of parameters with invariant thresholds, intercept and unique variances can be transformed to satisfy this condition using Transformation 32 with ${\mathbf{D}}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\Phi }}^{(g)})$, β^(g) = 0, ${\mathbf{\Delta }}^{(g)}={\text{diag}}^{\frac{1}{2}}({\mathbf{\sum }}^{(1)})$ and ${\mathit{\gamma }}^{(g)}=-{\text{diag}}^{-\frac{1}{2}}({\mathbf{\sum }}^{(1)})\mathit{\nu }$.

Condition 31 identifies this model. In fact, if it holds on both sides of Transformation 32, we have Δ⁽¹⁾ = I and D^(g) = I. The fourth equation in Transformation 32 implies Δ^(g) = Δ⁽¹⁾ = I. The first equation in Transformation 32 implies that γ^(g) does not depend on g, so we can drop its superscript. The condition ν̃ = ν = 0 implies γ = −Λ^(g)β^(g), which, similar to the reasoning in the proof of Proposition 8, implies β^(g) = 0 and γ = 0 for the general case where loadings on the same factor are not proportional across groups.

5.8. The comparison of factor means and variances

A related issue in the invariance of measurement parameters is whether each of the invariance levels discussed in this paper allows the comparison of factor means and factor variances. One way to address this question is to check whether the identification condition of this model involves setting all factor means to zero or all factor variances to one. If such constraints are present in the identification condition, factor means or factor variances cannot be compared because the null and alternative models in this comparison would be equivalent. For example, the invariance of loadings and unique variances does not allow the comparison of factor means, because Identification Condition 25 contains the constraint κ^(g) = 0 for all groups.

However, to confirm that a model allows the comparison of factor means (or variances) one need to make sure that all possible identification conditions of this model do not involve such constraints, which would not be discussed in this paper. Fortunately, because threshold invariance (for polytomous data) effectively equates the scales of the latent responses, the general rules for continuous outcomes apply. For example, since for continuous outcomes the invariance of loadings and intercepts guarantees the comparison of both factor means and variances, for ordered polytomous data one can do the same comparison with invariant thresholds, loadings and intercepts.

6. Nesting and Equivalence Relations

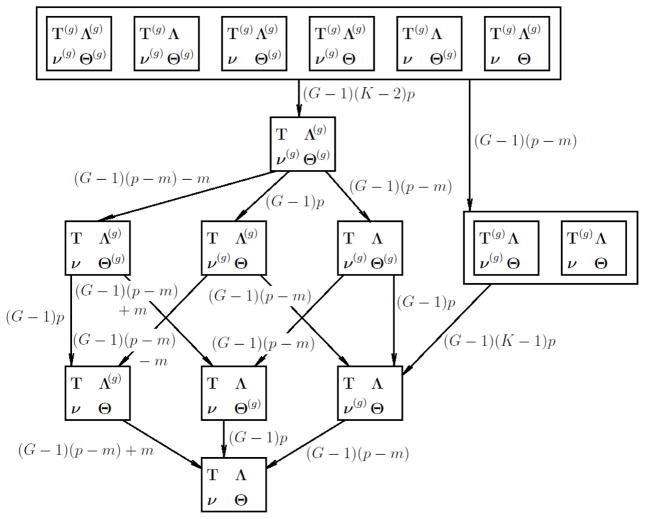
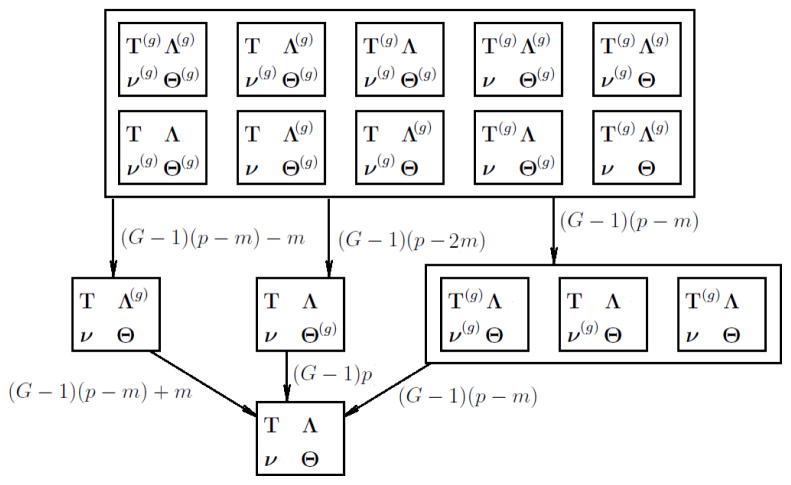
The number of different parameters in models with different levels of invariance is summarized in Tables 3 and 4 for ordered polytomous and binary data, respectively. Note that the symbols in the first column denote invariant parameters in a model. The 16 models with different levels of invariance form a hierarchy where the full measurement invariant model is the most constrained and the baseline model is the least constrained. This hierarchy is depicted in Figures 1 and 2 for polytomous and binary data. The nesting relationships among them are determined by their levels of invariance. For example, the model with invariant thresholds and unique variances is nested in the model with invariant thresholds only. In this case, the two models have the same identification conditions (Conditions 15 and 23) and the more restricted model can be obtained by applying additional constraints (in this case the invariance of unique variances) to the less restricted model. However, this is not always the case. Most nesting relationships among the 16 models are not obvious from the constraints they bear on their parameters. In most cases, when an additional invariance constraint is introduced, a part of the identification condition of the original model need to be removed because the newly introduced invariance provides information to identify additional parameters. For example, to obtain the model with invariant thresholds, loadings and unique variances from the model with only invariant loadings and unique variances, one need to remove the constraints on intercepts for G−1 groups in addition to adding the constraint of threshold invariance. This does not change their nesting relationship because the nesting relationship between two models is a relationship between the two sets of statistical distributions, not a relationship between their free parameters or the constraints on their parameters. This is related to the major point of this paper that an invariant model should not be built by simply applying invariance constraints on an identified baseline model. For example, in all three parameterizations of the baseline model listed in Table 3, item intercepts are fixed to zero, which need to be freed when a model with invariant thresholds is built.

Figure 1.

Nesting relations among models for polytomous items. Models are labeled by its parameters, where a superscript ^(g) denotes different parameters for different groups. Models in the same box are statistically equivalent. An arrow points from a less restricted model to a more restricted model in a nesting relationship. Expressions on the arrows show the difference in model dimensions.

Figure 2.

Nesting relations among models for dichotomous items. The structure is similar to Figure 1.

It is possible that adding one or multiple invariance conditions leads to an equivalent model. In this case, those invariance conditions cannot be tested because they can be satisfied trivially by a reparametrization. For example, not all invariance conditions imposes restrictions on the baseline model. Models with invariant loadings, intercepts or unique variances alone are equivalent to the baseline model. Each of those invariance conditions cannot be tested alone. Once thresholds are assumed invariant, invariance of loadings, intercepts and unique variances can be tested either separately or jointly. In light of this, we recommend investigating threshold invariance before considering other types of invariance. Once threshold invariance is established, the invariance of the remaining three types of parameters can be tested. For dichotomous items, more models are equivalent to the baseline model, but one is still able to compare models that are not statistically equivalent as depicted in Figure 2.

7. Singularities

It is not uncommon that an (otherwise) identified model is not identified on a subset of its parameter space. For example, a CFA model (for continuous items) with two standardized factors and two items per factor is identified, but when the factor correlation is zero, the remaining parameters are not identified; an otherwise identified mixture model is not identified when a mixture component (that involves unique parameters) has zero probability; a model with a covariance matrix of random effects parametrized in Cholesky decomposition is not identified when the true value of this covariance matrix is singular; a fixed effect 3PL IRT model can be identified by fixing the slope and difficulty of one item (Wu, accepted), but that is not enough for a fixed effect Rasch model with guessing (van der Linden and Barrett, 2016). These singularities occur at a lower dimensional subset of the parameter space, so they do not affect the identification of the model for almost the whole parameter space. However, if parameter estimates are close to this subset, the model is near un-identified and parameter estimation may suffer numerical instability.

Several models in this paper also have such singularities. The model with threshold and intercept invariance has singularities on the subset of its parameter space where loadings on the same factor are proportional across groups. The same situation arises for the model with invariant thresholds, intercepts and unique variances. The model for binary data with invariant thresholds, loadings and intercepts has singularities on the subset of its parameter space where the threshold to loading ratio is constant across items on the same factor.

Although these singularities do not affect the use of the model, the likelihood ratio test (LRT) statistic will generally not follow a χ² distribution if the true parameter values are in a singularity set of at least one of the two compared models (e.g. Drton, 2009). For example, it is well known that in mixture modeling the LRT for the number of mixture components is a nonstandard test (Davies, 1977, 1987; Jeffries, 2003) and that tests on singular multivariate variance components suffer from the same problem (Carey, 2005; Wu and Neale, 2013). For the CFA models discussed above, the LRT comparing a full measurement invariance model and a model with only threshold and intercept invariance is a nonstandard test because under the null hypothesis, the true model has equal loadings across groups, falling in the singularities of the alternative model. In this test, the asymptotic distribution of the LRT statistic may not be χ² distributed.

8. Numerical Illustration and Simulation Studies

8.1. A numerical illustration of equivalence relations

We introduce an numerical illustration to demonstrate the equivalence relationships in the first box in Figure 1. Consider a model for four ternary items of one standardized latent factor in two groups and let parameters take true values in the row “Set I” of Table 5. These parameters satisfies Identification Condition 7 in each group and also invariance of intercepts. They imply the following correlations for the latent responses for the two groups:

$${\mathbf{P}}^{(1)}=\left(\begin{array}{cccc}1& 1/4& \sqrt{2}/4& \sqrt{2}/4\\ 1/4& 1& \sqrt{2}/4& \sqrt{2}/4\\ \sqrt{2}/4& \sqrt{2}/4& 1& 1/2\\ \sqrt{2}/4& \sqrt{2}/4& 1/2& 1\end{array}\right)\text{and}{\mathbf{P}}^{(2)}=\left(\begin{array}{cccc}1& 3/4& 1/2& 1/2\\ 3/4& 1& 1/2& 1/2\\ 1/2& 1/2& 1& 1/3\\ 1/2& 1/2& 1/3& 1\end{array}\right).$$

Table 5.

Four sets of parameters that produce the same model implied probabilities for response patterns of four ternary items in two groups. For all four cases, the latent factor is standardized. The first set gives standardized parameters. The second set has loading and intercept invariance. The third set has invariant unique variances and intercepts. The fourth set satisfies threshold invariance.

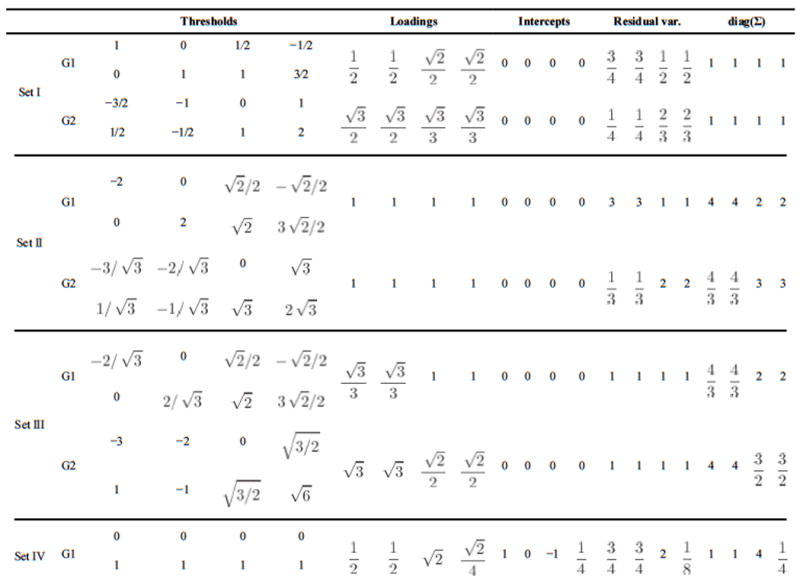
The standardized thresholds are the same as the thresholds because the latent responses are standardized under this parametrization. Below we will transform this set of true parameter values into three different sets of parameter values that satisfy different invariance conditions without changing the model implied standardized thresholds and polychoric correlations.

Because a configural invariant model is equivalent to a model with invariant loadings (see Proposition 5), we can transform the parameters to satisfy Identification Condition 17 using Transformation 11. Details of this transformation are given in the proof of Proposition 5. An easier account of this transformation is that both thresholds of an item in Set I are divided by the loading of that item to produce the transformed thresholds and its residual variance is divided by the squared loading to produce the transformed residual variance. The resultant parameters are listed in the row “Set II” of Table 5, where all factor loadings become one.

The row “Set III” of this table shows another parameterization of the same true values. Now the parameter values satisfy Identification Condition 8 in each group and the invariance of both intercepts and unique variances. This time the loading and thresholds of an item in Set I are divided by the square root of its residual variance to produce the transformed values.

For ternary data, the model with configural invariance is equivalent to the model with threshold invariance (see proposition 2). We can transform the parameters to satisfy threshold invariance. The resultant parameters are in row “Set IV” of Table 5.

It is straightforward to find that all four sets of parameters imply the same correlations for the latent responses as shown above and the same standardized thresholds. As a result, they also imply the same probabilities for response patterns. Since the common factors stay standardized, the only difference across the four sets of parameters is the scale of the four latent responses. This illustration shows that for ordered ternary data, any set of parameters with configural invariance can be transformed to satisfy the invariance of thresholds, of loadings and intercepts, or of intercepts and unique variances. As a result, there is no degree of freedom to test these invariance conditions.

8.2. Simulation studies

We now introduce two simulation studies to demonstrate the regular and singular nesting relations among the models. For regular nesting relations we expect a difference test with ML estimation to produce an asymptotic χ² distribution; for singular nesting relations the test statistic may not have a χ² distribution. This simulation study also verifies the dfs marked in Figures 2 and 1.

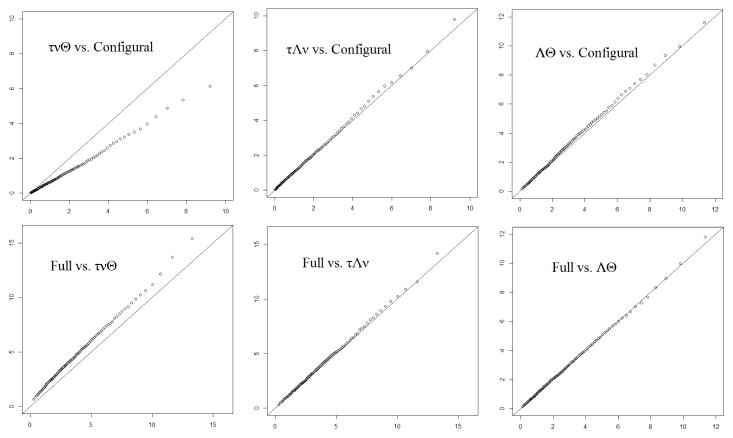
In the first simulation, binary data were generated with a single factor model with four indicators in two groups. The true parameter values satisfy full measurement invariance. The four loadings are 0.7, 0.7, 0.5 and 0.5. The unique variances are 0.51, 0.51, 0.75 and 0.75. The intercepts are all zero. The four thresholds are equally space between −0.5 and 1. The factor variances are 1 and 2.25 for the two groups. The factor means are 0 and 1. The per group sample size is 1000. 2000 replications are used. For each replication, all five statistically non-equivalent models in Figure 2 were fitted using OpenMx with ML estimation⁵ and all models converged.

Each arrow in Figure 2 corresponds to a nesting relationship and a difference test. The 1st-99th percentiles of the LRT statistic of the six difference tests are plotted in the six panels of Figure 3 against those of a χ² distribution with the desired dfs marked on the arrows in Figure 2. In the upper left corner of each panel the null and alternative models of this LRT are marked. Greek letters represent the invariant parameters. “Full” refers to the model invariant in all four types of parameters. Among the six panels, four show a good alignment between the empirical and desired distribution of the LRT statistic. The remaining two panels are tests that involve the model with invariant thresholds, intercepts and unique variances. As discussed in Sections 7, this model involves singularities and the true parameter values of this simulation is in the singularities of this model, so the resultant LRT statistic does not have the desired χ² distribution.

Figure 3.

Plots of the 1st-99th percentiles of the simulated distribution of the LRT statistic against those of a χ² distribution with appropriate dfs. Data are dichotomous. Each panel corresponds to a difference test represented by an arrow in Figure 2. Greek letters denote invariant parameters in a model.

The second simulation study is the same to the first study except that the outcomes are in four categories with the following true threshold matrix (four columns for four items)

$$\mathbf{T}=\left(\begin{array}{cccc}-0.5& -0.25& 0& 0.25\\ -0.25& 0& 0.25& 0.5\\ 0& 0.25& 0.5& 0.75\end{array}\right)$$

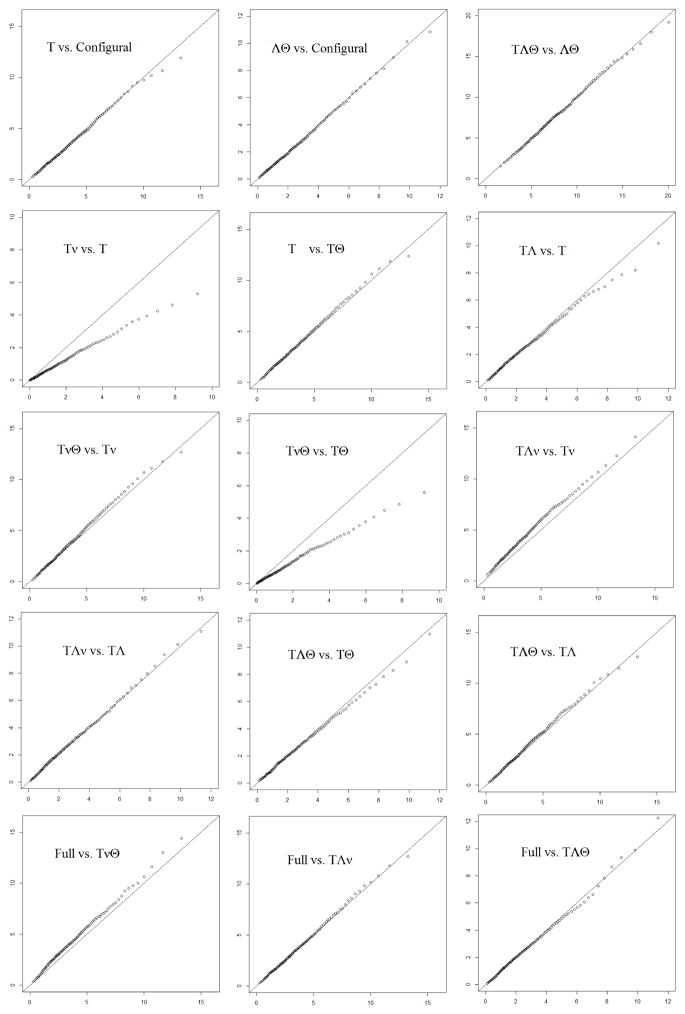
The per-group sample size and number of replications are both 2000. For each replication, all 10 statistically non-equivalent models in Figure 1 were fitted using OpenMx with ML estimation. Except one replication which did not converge when fitted to the model with threshold and intercept invariance, all other models and replications converged.

Each arrow in Figure 1 corresponds to a nesting relationship and a difference test. The 1st-99th percentiles of the LRT statistic of the 15 tests are plotted in the 15 panels of Figure 4 against those of a χ² distribution with dfs marked on the arrows in Figure 1. The two nested models are marked on the upper left corner of each panel in the same way as in Figure 3. In four of the 15 panels the LRT does not produce a statistic with the desired χ² distribution. These four tests involve either the model with threshold and intercept invariance or the model with invariant thresholds, intercepts and unique variances. Again, this happens because the true parameters of this simulation lies on the singularities of both models. Interestingly, the distribution of the LRT statistic comparing these two models seems to be close to the desired χ² distribution even though the regularity condition is still violated. All remaining panels of this figure show a good alignment between the theoretical and simulated distributions of the statistic.

Figure 4.

Plots of the 1st-99th percentiles of the simulated distribution of the LRT statistic against those of a χ² distribution with appropriate dfs. Data are in four categories. Each panel corresponds to a difference test represented by an arrow in Figure 1. In each panel, Greek letters denote invariant parameters in a model.

9. Model Specifications in Mplus and OpenMx

For ordered categorical data from multiple groups, Mplus (Muthén and Muthén, 1998–2012) imposes several default constraints on the parameters. Some of these constraints can be overridden by carefully specifying all parameters explicitly in the MODEL command. However, some default cannot be overridden easily. For example, the intercepts are fixed at 0 for ordered categorical data. This is hard to override because intercept parameters are not explicitly specified in the MODEL command. Below we give an alternative way to specify models with which all the 16 models discussed above can be specified easily.

To specify a model with ordered categorical data with explicit intercept parameters, one may explicitly specify the unobserved response variables y^* as latent indicator variables of the factors and then specify the observed categorical variables as single indicators of the y^*’s. The loadings of these single indicators must be fixed to 1 and the error variances of the y^* variables must be fixed at 0. The intercepts of these y^* variables can then be explicitly specified as the intercepts of the ordered categorical variables. In the Appendix, a model with a single common factor, four indicators and two groups is specified in this way. Threshold and loading invariance is imposed.

In OpenMx (Boker, Neale, Maes et. al., 2011; Neale, Hunter, Pritkin et. al., 2015), a model can be specified by defining the threshold, mean and covariance structures as matrix valued functions of parameters. Equality constraints on model parameters are specified by using the same label to corresponding elements in the matrices. Although a functional constraint such as diag(Σ) = I can be specified using mxConstraint, it adds to the computational complexity and should be avoided if possible. We recommend that users specify the diagonal elements of diag(Σ) as explicit parameters if they are set to one in the model and express the unique variances as a function of parameters if needed. The OpenMx code of a model for binary data with invariant loadings and unique variances is illustrated in the Appendix. It has one common factor and four indicators.

10. Summary and Conclusion

Studies of measurement invariance for ordered categorical data usually proceed by first identifying the model with only configural invariance as a baseline and then introducing additional invariance constraints to build a hierarchy of models. In this approach, the scale of the latent responses is set by the identification condition used in the baseline model and all subsequent additional invariance constraints are built on this particular scale. This may lead to the incorrect rejection of parameter invariance if the original parameters are invariant under some different scale of the latent responses. This would also lead to different conclusions for different choices of identification condition for the baseline model. Mathematically, these occur because the identification condition used in the baseline model may become restrictions when additional invariance conditions are introduced. In this article we advocate an approach where each model in the invariance hierarchy is identified separately based on Transformation 11 that reveals the four sources of non-identifiability of the CFA model for ordered categorical data. In this approach models with different levels of invariance are not defined through modification of the baseline model and are therefore not affected by its identification condition. Using this approach we give the identification condition for models with different levels of invariance. We also find that the invariance of some parameters cannot be tested alone. For example, the invariance of loadings can not be tested when there is no threshold invariance. For data with more than two categories, we recommend that invariance be tested first for thresholds, and then proceed to other parameters.

This article only discusses the invariance of all parameters of the same type (e.g. the invariance of all loading parameters), but not partial invariance (see, e.g., Millsap and Meredith, 2007, pp.145–149) where parameters are invariant only for some of the items. Tests of partial invariance for continuous data are sensitive to the how the model is standardized and the choice of the reference items (Cheung and Rensvold, 1998, 1999; Rensvold and Cheung, 2001), a problem of the same essence as discussed here, and has the additional issue of specification search (Oort, 1998; Yoon and Millsap, 2007). For ordered categorical data, the issue of identification will be more complex due to the presence of threshold parameters. Identification conditions for partially invariant models for ordered categorical data are beyond the scope of this article.

Testing measurement invariance in categorical data is inherently complex due to the sometimes competing needs of identification and invariance constraints. Given the importance of measurement invariance to substantive work, we urge researchers to exercise great care in selecting identification conditions to yield testable and interpretable measurement structures.

A. Mplus and OpenMx Codes

A.1. Model specification in Mplus

 

TITLE: A model with invariant thresholds and loadings of two groups,
             one common factor, four indicators and five categories per indicator
DATA: FILE IS (file name)
VARIABLE: NAMES ARE x1 x2 x3 x4 group;
                      USEVARIABLES ARE x1 x2 x3 x4 group;
                      GROUPING IS group (0=male 1=female);
                      CATEGORICAL ARE x1 x2 x3 x4
ANALYSIS: ESTIMATOR IS WLSMV;
MODEL:
               y1 By x1@1;
               y2 By x2@1;
               y3 By x3@1;
               y4 By x4@1;
               factor BY y1* (L1) y2 (L2) y3 (L3) y4 (L4);
               factor@1;
                [factor@0];
               {x1-x4@1};
                [y1-y4@0];
               y1-y4@0;
                [x1$1-x1$4*](T1-T4);
                [x2$1-x2$4*](T5-T8);
                [x3$1-x3$4*](T9-T12);
                [x4$1-x4$4*](T13-T16);
MODEL female:
               factor BY y1* (L1) y2 (L2) y3 (L3) y4 (L4);
               factor*;
                [factor@0];
               {x1-x4*};
                [y1-y4*];
               y1-y4@0;
                [x1$1-x1$4*](T1-T4);
                [x2$1-x2$4*](T5-T8);
                [x3$1-x3$4*](T9-T12);
                [x4$1-x4$4*](T13-T16);

A.2. Model specification in OpenMx

 

# A model with invariant loadings and unique variances of two groups,
# one common factor, four indicators and two categories per indicator
library(OpenMx)
group1data <- read.table(“myGroup1Data.txt”);
group2data <- read.table(“myGroup2Data.txt”);
items <- 4;
label.tau<-paste(“t”,1:items,sep=““);
# specify components
tau<-mxMatrix(“Full”,1,items,TRUE,c(-.5,0,.5,1),label.tau, name=“tau”);
L<-mxMatrix(“Full”,1,items,TRUE,0.8,paste(“l”,1:items,sep=““),
lbound=0.001, name=“L”);
nu<-mxMatrix(“Full”, 1,items,FALSE, 0,paste(“n”,1:items,sep=““),name=“nu”);
D<-mxMatrix(“Diag”,items,items,FALSE,1,paste(“d”,1:items,sep=““),name=“D”);
Phi<-mxMatrix(“Symm”,1,1,FALSE,1,”facVar”,name=“Phi”);
alpha<-mxMatrix(“Full”,1,1,FALSE,0,”a”,name=“alpha”);
Theta<-mxAlgebra(D-vec2diag(diag2vec(t(L)%*%Phi%*%L)),name=“Theta”);
Sigma<-mxAlgebra(t(L)%*%Phi%*%L+Theta,name=“Sigma”);
M<-mxAlgebra(alpha%*%L+nu,name=“M”);
# specify group 1 and then group 2 by altering group 1.
group1 <- mxModel(L, Phi, D, Theta, Sigma, nu, alpha, M, tau,
  mxExpectationNormal(“Sigma”, “M”, paste(“X”, 1:items, sep=““),”tau”),mxFitFunctionML())
group2 <- omxSetParameters(group1, labels=label.tau,
newlabels=paste(“t”, 1:items, “2”, sep=““),free=TRUE, name=“G2”);
group2<-omxSetParameters(group2, labels=“facVar”,newlabels=“facVar2”, free=TRUE);
Theta2<-mxAlgebra(G1.Theta, name=“Theta”);
group2$Theta<-Theta2;
group2$D<-NULL;
# add data, combine two groups and run model
G1<-mxModel(group1,mxData(group1data, “raw”), name=“G1”);
G2<-mxModel(group2,mxData(group2data, “raw”), name=“G2”);
multiGroup <- mxModel(“multiGroupModel”, G1, G2,
     mxAlgebra(G1.fitfunction + G2.fitfunction, name=“obj”),mxFitFunctionAlgebra(“obj”));
mgRes <- mxRun(multiGroup)
summary(mgRes)