Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2017 Jun 1;8:15687. doi: 10.1038/ncomms15687

Polymorphism in a high-entropy alloy

Fei Zhang 1,2,*, Yuan Wu 1,*, Hongbo Lou 2,*, Zhidan Zeng 2, Vitali B Prakapenka 3, Eran Greenberg 3, Yang Ren 4, Jinyuan Yan 5,6, John S Okasinski 4, Xiongjun Liu 1, Yong Liu 7, Qiaoshi Zeng 2,8,a, Zhaoping Lu 1,b
PMCID: PMC5461481  PMID: 28569758

Abstract

Polymorphism, which describes the occurrence of different lattice structures in a crystalline material, is a critical phenomenon in materials science and condensed matter physics. Recently, configuration disorder was compositionally engineered into single lattices, leading to the discovery of high-entropy alloys and high-entropy oxides. For these novel entropy-stabilized forms of crystalline matter with extremely high structural stability, is polymorphism still possible? Here by employing in situ high-pressure synchrotron radiation X-ray diffraction, we reveal a polymorphic transition from face-centred-cubic (fcc) structure to hexagonal-close-packing (hcp) structure in the prototype CoCrFeMnNi high-entropy alloy. The transition is irreversible, and our in situ high-temperature synchrotron radiation X-ray diffraction experiments at different pressures of the retained hcp high-entropy alloy reveal that the fcc phase is a stable polymorph at high temperatures, while the hcp structure is more thermodynamically favourable at lower temperatures. As pressure is increased, the critical temperature for the hcp-to-fcc transformation also rises.

Whether a polymorphic transition exists in high entropy alloys or not remains unclear since discovery of these alloys more than a decade ago. Here authors report an irreversible polymorphic transition from fcc to hcp in the prototype FeCoCrMnNi high entropy alloy and provide evidence for fcc phase being more stable than hcp phase only at high temperatures.

Polymorphism, which refers to the ability of a solid material to exist in more than one crystal structure, is widely observed in many materials including polymers1, minerals2,3,4 and metals5,6,7,8. The polymorphic transition is a well-known yet critical phenomenon in nature and surprisingly, polymorphs with identical compositions can have different physical, chemical and mechanical properties due to different structural characteristics, which have attracted considerable attention over the last few decades9,10,11. Pressure and temperature are usually controlling parameters for inducing these transitions by altering the atomic and/or electronic structures and creating novel materials. For example, carbon can take on graphite and diamond under different pressures and temperatures.

Recently, a new alloy design concept based on entropic contributions to the thermodynamic landscape, rather than cohesive energy, was proposed12,13, which was subsequently extended to non-metallic systems such as multicomponent oxides14. This strategy was explored by deliberately incorporating five or more elemental species into a single lattice with random site occupancy. Due to the engineered configuration disorder, these entropy-stabilized solid solution alloys, that is, high-entropy alloys (HEAs), usually show a single-phase structure with high symmetry and extremely attractive properties15,16,17,18,19,20,21. Among various reported HEAs in literature, the equiatomic CoCrFeMnNi alloy (also termed as Cantor's alloy)12,13 is a prototype fcc (face-centred-cubic) HEA, which possesses ultrahigh fracture toughness and large ductility, even at cryogenic temperatures19,22,23. It is generally believed that HEA lattices are severely distorted and atomic diffusion is extremely sluggish due to the chemical complexity and packing disorder24,25. Consequently, HEAs have exceptionally high microstructural stability26,27. Many studies also demonstrate that the CoCrFeMnNi HEA can maintain its fcc structure over a large temperature range from cryogenic temperatures up to the melting temperature without any polymorphic phase transition19,22,28. Considering the extensive polymorphism in the typical constituent elements of HEAs, such as Fe, Co and Mn29, an intriguing question is naturally raised: when metallic alloys are made in the entropy-stabilized form of crystalline matter with high structural stability, is polymorphism still possible?

More recently, long-term annealing experiments at intermediate temperatures revealed that different crystalline phases could precipitate out of the CoCrFeMnNi HEA fcc matrix27,30,31. Moreover, finite-temperature ab initio simulation results suggest that the free energy of the hcp (hexagonal-close-packing) crystallographic lattice in the CoCrFeMnNi HEA may be lowest at room temperature, compared with that of its bcc (body-centerd-cubic) and fcc counterparts32,33. All these results cast doubt on the high structural stability of HEA lattices, which is obviously a critical and vital problem for our understanding and applications of these newly developed metallic materials and multicomponent oxides. However, until now the predicted hcp phase of the CoCrFeMnNi HEA has not been observed in any experiments and the question of viable polymorphism remains unanswered.

In this work, we employed an in situ high-pressure synchrotron radiation X-ray diffraction (XRD) technique and discovered a polymorphic transition from fcc to hcp in the prototype CoCrFeMnNi HEA under hydrostatic compression at room temperature. The phase transition is sluggish, it starts at ∼22 GPa and almost completes at ∼41 GPa, and the hcp phase could be retained when the pressure was totally released, which is the first synthesis of the CoCrFeMnNi HEA with an hcp structure at ambient conditions. Our in situ laser/resistive heating XRD experiments at different pressures show an inverse transition from hcp back to fcc at elevated temperatures and reveal that the fcc phase is stable at high temperatures while the hcp structure is more thermodynamically favourable at relatively lower temperatures. Our findings indicate that this fcc HEA is a thermodynamically metastable polymorph obtained by kinetic constraints and the thermodynamically favourable hcp structure is relatively difficult to attain.

Results

Microstructure and compositional analysis

The CoCrFeMnNi HEA sample was synthesized using a gas-atomization technique34. The gas-atomized powders are spherical particles with a typical size ranging from a few microns to tens of microns, which are appropriate for high-pressure experiments (Supplementary Fig. 1). These particles are polycrystalline with a grain size ranging from submicron to a few microns (the inset of Supplementary Fig. 1). The chemical and energy dispersive X-ray spectroscopy analyses confirm that the composition of the as-atomized CoCrFeMnNi HEA is close to the nominal composition, and there are no compositional changes after the high-pressure XRD tests (Supplementary Fig. 2 and Supplementary Table 1).

In situ high-pressure synchrotron XRD at room temperature

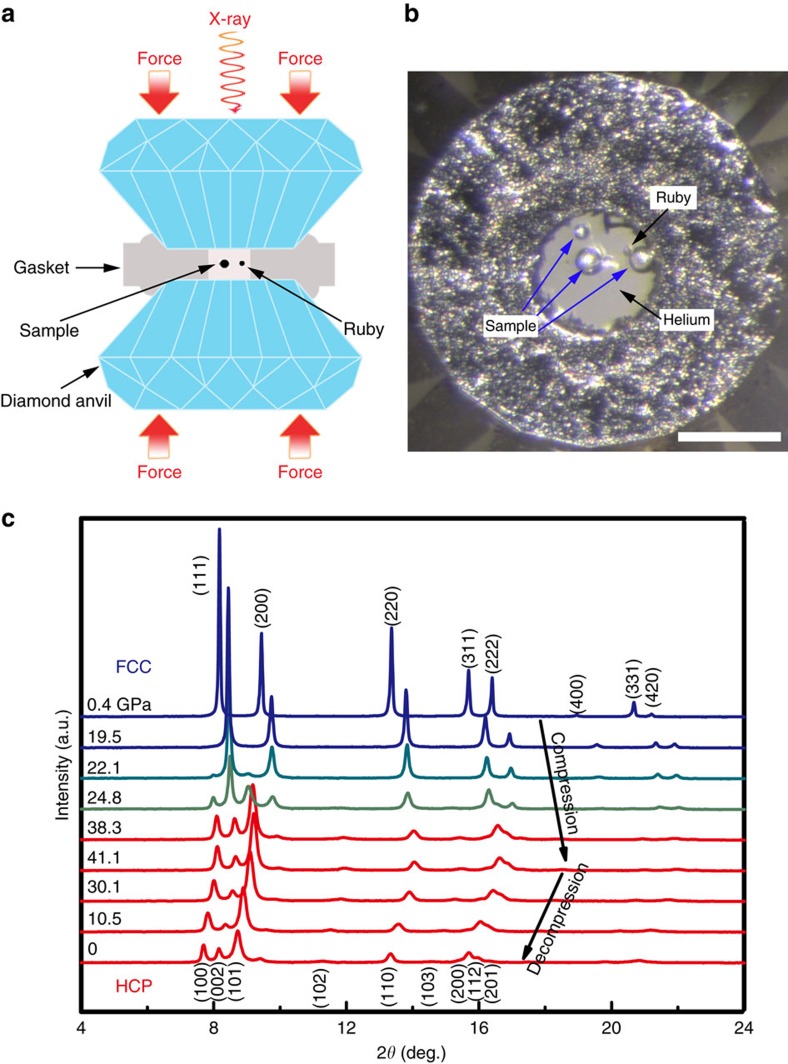
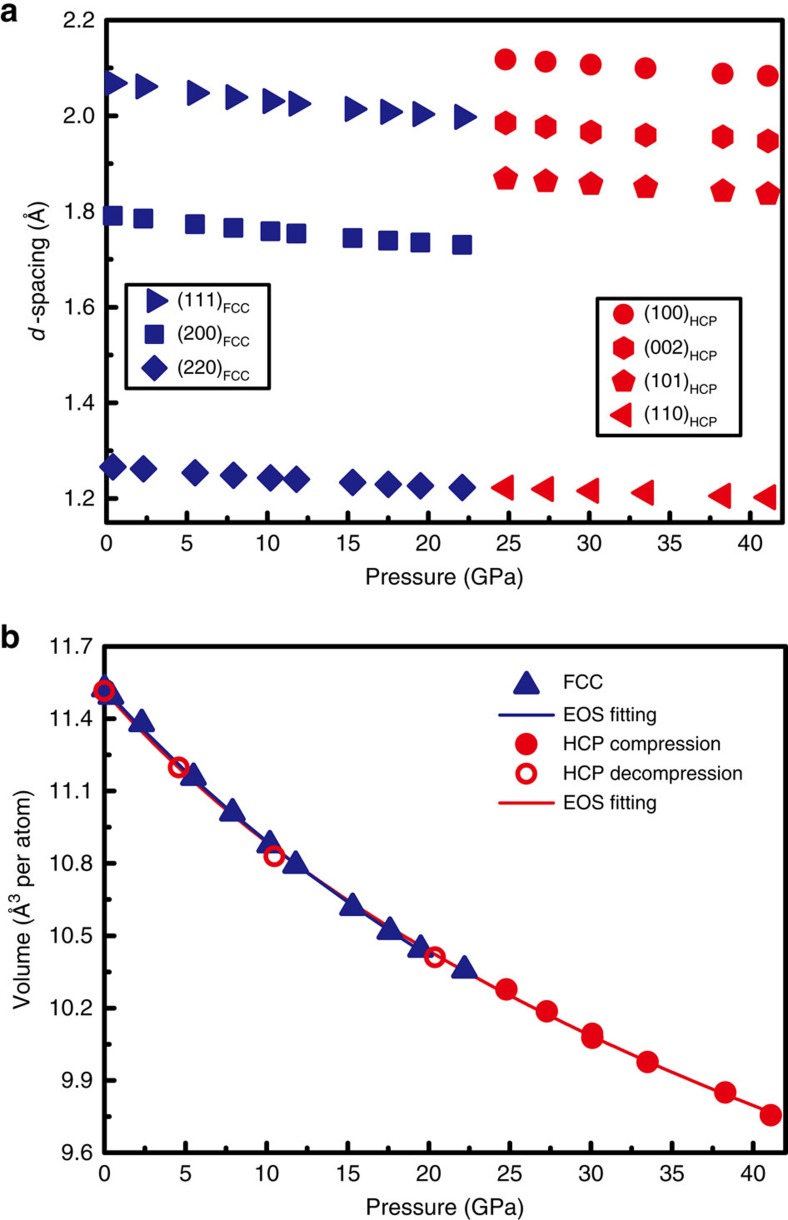
Hydrostatic pressure up to ∼41 GPa was applied to the tiny CoCrFeMnNi HEA particles using a diamond anvil cell (DAC). The experimental set-up of the DAC and the sample loading image are shown in Fig. 1a,b, respectively. More details can be found in Methods. The structural evolution of the CoCrFeMnNi HEA during compression was monitored by high-brightness synchrotron radiation XRD through two transparent diamond anvils of the DAC. The XRD patterns collected from both the compression and decompression processes are shown in Fig. 1c. The initial HEA sample has an fcc single-phase structure, which remains stable up to 19.5 GPa. All diffraction reflections shift towards higher 2θ values, which is an expected result of the pressure-induced volume decrease. Once the pressure approaches 22.1 GPa, extra diffraction peaks beside the (111) peak of fcc appeared (indicated by red triangles in Fig. 1c), suggesting the occurrence of a phase transition. With further increasing pressure, the intensity of the fcc peaks was obviously lowered, while that of the new diffraction peaks increased appreciably. The transition was sluggish, the fcc and new phase coexisted over large pressure range. At the maximum pressure of ∼41 GPa, the diffraction reflections mainly corresponded to the new phase while only minute residual fcc phase remained. During decompression, surprisingly the phase transition was irreversible. The newly formed phase was completely retained down to ambient pressure. All the new phase peaks were well indexed as crystallographic reflections of an hcp lattice (space group P63/mmc), which revealed an fcc-to-hcp transition under high-pressure in the prototype CoCrFeMnNi HEA (Table 1 and Supplementary Fig. 3). Detailed information about their structure, such as the interplanar d-spacing (Fig. 2a) and unit cell volume (Fig. 2b) as a function of the applied pressure, was obtained by fitting the measured compression and decompression XRD patterns using the Le Bail method in the standard GSAS package35. The c/a ratio of the hcp phase remained almost constant at 1.62±0.01 during both compression and decompression. These two sets of volume data in Fig. 2b can be well fitted by a third-order Birch-Murnaghan isothermal equation of state (EOS)36, with the isothermal bulk modulus B0=153.9±3.0 GPa and its pressure derivative 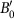Inline graphic=4.9±0.7 for the fcc phase and B0=150.2±4.6 GPa and 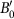Inline graphic=6.2±0.5 for the hcp phase. The bulk moduli obtained in this work are consistent with previous experimental results28 on the fcc phase and simulation results33,37 on both the fcc and hcp phases. The two phases exhibit no obvious difference in both volume and bulk modulus. It should be noted that the grain size of the sample is still not small enough to obtain smooth diffraction rings, as compared with the tiny X-ray beam size (2.5 × 4 μm2). Therefore, the relative intensity of the different peaks is not statistically reliable for the Rietveld refinement to accurately derive the volume fractions of the fcc and hcp phases during the transition. Alternatively, by assuming the phase fraction is proportional to the area of corresponding diffraction peaks, such as the fcc-(200) and hcp-(101) peak areas in Fig. 1c, the volume fraction of hcp as a function of pressure during both compression and decompression can be roughly estimated (Supplementary Fig. 4). The results in Supplementary Fig. 4 confirm that the transition is sluggish over a wide pressure range and irreversible with an almost constant volume fraction of hcp during the decompression.

Figure 1. Experimental set-up and the in situ high-pressure XRD patterns of the CoCrFeMnNi HEA in a DAC during compression and decompression at room temperature.

Figure 1

Open in a new tab

(a,b) A schematic illustration of the DAC used to generate high-pressure on tiny samples for the in situ high-pressure experiment. (c) XRD patterns as a function of pressure obtained during compression and decompression with a X-ray wavelength λ=0.2952 Å. The initial phase is indexed to an fcc lattice, whereas the new phase synthesized above 22 GPa is well indexed to an hcp lattice. Intensity mismatch of the standard fcc and hcp structures is caused by the relatively large grains in the samples. The scale bar in b represents 100 μm.

Table 1. Unit-cell parameters and d-spacings of the different (hkl) planes of both the fcc and hcp CoCrFeMnNi HEAs at different pressures.

(hkl) fcc
 (hkl) hcp
  dobs, (Å) dcal, (Å) dobs, (Å) dcal, (Å)   dobs, (Å) dcal, (Å) dobs, (Å) dcal, (Å)
111 2.071 2.073 2.005 2.003 100 2.081 2.083 2.200 2.196
200 1.794 1.795 1.737 1.735 002 1.954 1.947 2.075 2.069
220 1.268 1.269 1.228 1.226 101 1.838 1.837 1.941 1.939
311 1.082 1.083 1.048 1.046 110 1.202 1.202 1.271 1.267
P, GPa 0.4 19.5   41.1 0.0
a, c, Å 3.582(1) 3.470(1)   a=2.405 (1) a=2.535(2)
        c=3.895(1) c=4.138(1)
V, Å3 11.493(1) 10.444(1)   9.7551(1) 11.5145(2)
Open in a new tab

The subscript ‘obs' represents experimentally observed values and ‘cal' represents values from the Le Bail refinement.

Figure 2. Pressure dependence of the CoCrFeMnNi HEA d-spacings and volume.

Figure 2

Open in a new tab

(a) The pressure dependence of the d-spacings associated with the major Bragg peaks of fcc (shown in blue symbols) and hcp (shown in red symbols), respectively. The error bars are smaller than the symbol sizes. (b) The average volume per atom for both the fcc (blue triangles) and hcp phases (red solid circles for compression and red open circles for decompression) are calculated as a function of pressure. The volume data can be well fitted using the third-order Birch-Murnaghan EOS for both fcc (blue solid line) and hcp (red solid line). The EOS of fcc and hcp almost coincides with each other, showing no obvious volume difference at any given pressure.

In situ laser/resistive heating synchrotron radiation XRD

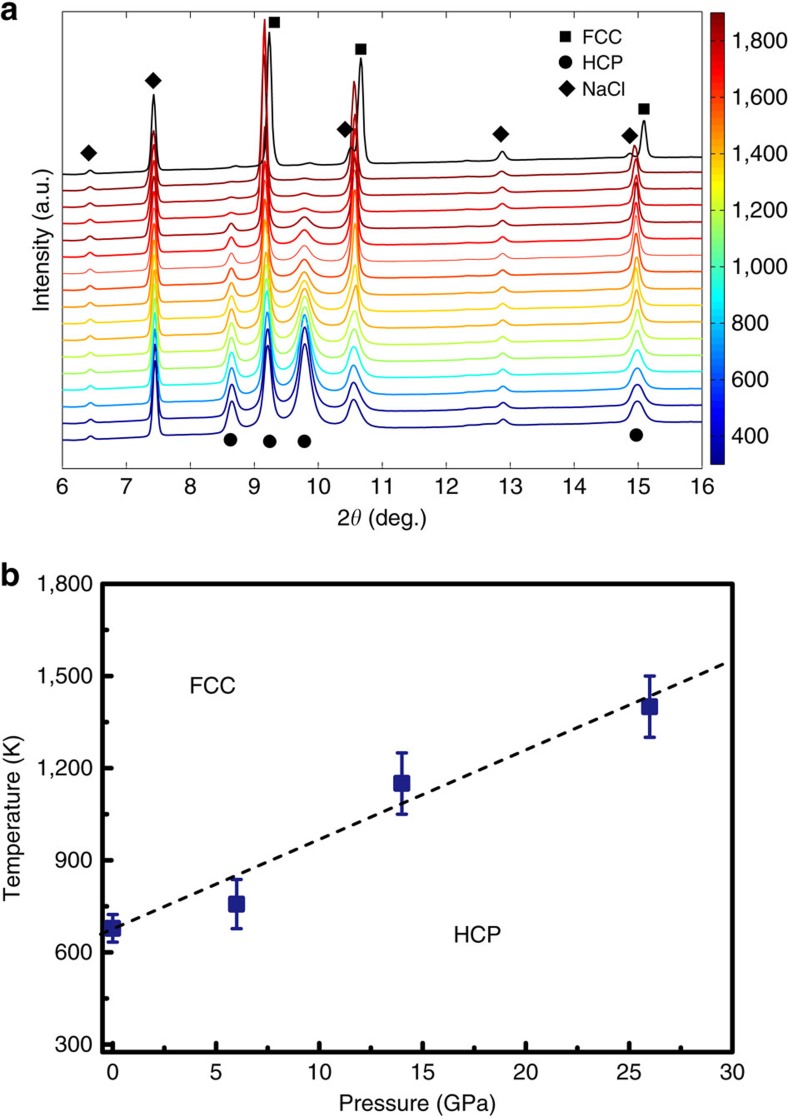
The irreversibility of the phase transition questions the relative stability of the fcc and hcp phases. To clarify this, in situ heating XRD studies were carried out at different pressures on the synthesized hcp phase. At ambient pressure, the hcp sample was sealed in a resistive heating DAC using silicone oil to prevent oxidation of the tiny sample. The hcp phase remained stable up to 633 K at ambient pressure, and almost completely transformed back to fcc when heated up to 723 K (Supplementary Fig. 5). Once the pressure was increased, the critical transition temperature significantly increased, which is beyond the limit of the resistive heating DAC. Therefore, a double-sided Nd:YLF laser heating system coupled with a DAC was employed to heat the hcp phase at higher pressures of 6, 14 and 26 GPa. As an example, Fig. 3a presents the in situ laser heating XRD patterns collected at 26 GPa. With continuous heating above ∼1,400 K at 26 GPa, the fcc phase started to gradually grow at the expense of the hcp phase. Therefore, the temperature of ∼1,400 K was determined to be the critical temperature (fcc-in) for the phase transition. Based on four critical transition temperatures determined at different pressures, a boundary is proposed in Fig. 3b.

Figure 3. In situ laser heating XRD of the CoCrFeMnNi HEA at different pressures.

Figure 3

Open in a new tab

(a) The XRD patterns as a function of temperature from room temperature to 1,850 K with an X-ray wavelength of ∼0.3220 Å. The intensity of the major hcp peaks is almost constant below 1,400 K, but starts to gradually decrease during continuous heating above ∼1,400 K, indicating the critical transition temperature occurs at ∼1,400 K. (b) The temperature and pressure metastability boundary (not the equilibrium phase boundary) of the hcp CoCrFeMnNi HEA. The critical transition temperature is determined as the first appearance temperature of the fcc phase from the hcp phase (synthesis curve of the fcc phase) during heating at different pressures and it increases with pressure. The error bars of temperatures were estimated by the fitting errors of the blackbody radiation spectra and the temperature difference between two sides of the sample.

Discussion

The structural stability of the prototype CoCrFeMnNi HEA has been extensively studied in a wide temperature range from 55 K to its melting temperature of ∼1,600 K at ambient pressure19,31,37,38 but to our knowledge, no polymorphic transition has been observed. Conversely, high-pressure studies remain a virgin area in HEAs. In this work, using in situ high-pressure XRD techniques, we observed the first polymorphic transition from fcc to hcp in the CoCrFeMnNi HEA, as shown in Fig. 1c. Therefore, some critical questions are how and why can an hcp HEA form at high-pressure and can it be maintained at ambient conditions? According to the d-spacing of the main reflections of both fcc and hcp (that is, (111) and (220) of fcc, and (100), (002), (101) and (110) of hcp, as a function of pressure shown in Fig. 2a), it is clear that the hcp-(002) and hcp-(110) planes inherit the fcc-(111) and fcc-(220) planes, respectively. In addition, Fig. 2b shows no obvious volume collapse during the transition; both the fcc and hcp phases seem to have almost the same volume per atom and bulk modulus. This is similar to many other fcc to hcp martensitic transitions, such as in cobalt39 or xenon40, which also show weak first-order features.

It is well known that the fcc and hcp lattices only differ in the stacking sequence of the close packing layers, for example, the fcc and hcp crystal lattices follows the pattern of ABCABCABC…along the fcc [111] direction and ABABAB…along the hcp [001] direction, respectively. The hcp structure can be readily obtained locally from a fcc structure by introducing stacking faults. And it can be easily realized in the current HEA because recent experiment41 and simulations37,41 have confirmed that it indeed has a low staking fault energy of ∼20 mJ m−2. However, the detailed mechanism of this transition could be much complex since the stacking faults, dislocations, and twining events may be all involved, and the magnetic states and volume (high pressure tuning) of the HEA alloy could also affect the transition behaviour32,33,42,43.

As shown in Fig. 3, the results of the in situ heating XRD experiments at different pressures explicitly demonstrate that the hcp phase of the CoCrFeMnNi HEA is relatively stable at low temperatures and high pressures, while the fcc phase is actually stable at higher temperatures and lower pressures, showing a boundary in between them with a positive slope. Using ab initio calculations, Ma et al.32 actually revealed that thermodynamically, the CoCrFeMnNi HEA prefers the hcp structure below 340 K at ambient pressure and paramagnetic state while the fcc phase dominates at higher temperatures, which is qualitatively consistent with our experimental observations. It should be noted that in our experiment the phase transitions were sluggish and irreversible, suggesting high energy barriers between the hcp and the fcc phases, therefore overshooting often exists. It is difficult to determine the real equilibrium phase boundary (that is, the Clapeyron coexistence curve) experimentally. The curve in Fig. 3b is actually a synthesis curve showing the first appearance of the fcc phase (fcc-in) from the hcp phase. During cooling, the fcc phase was fully recovered to room temperature showing a large metastability range. The real equilibrium phase boundary between fcc and hcp may be much lower than 633 K observed in experiments. According to Ostwald's Rule44, high-temperature polymorphs often form first during cooling/crystallization. In other words, with conventional preparation techniques such as melt casting and atomization, the CoCrFeMnNi HEA always forms the fcc structure first, and when cooled down to room temperature, the transition from fcc to hcp likely depends on the entire complex γ-surface and could be kinetically hindered32,42,45. However, nano-twinning has been observed in the CoCrFeMnNi HEA at cryogenic temperatures (77 K) (ref. 19). This observation indicates that the stacking fault energy may diminish with decreasing temperature, which could facilitate the sliding needed for a displacive phase transition from fcc to hcp32. Recent theoretical work studied the stacking fault energy as a function of temperature in the CoCrFeMnNi HEA and confirmed this speculation33,37. Compared with temperature, pressure is a more powerful parameter in terms of decreasing the volume, tuning packing and energy state of a sample. The polymorphic transition from fcc to hcp unveiled in this work demonstrates that high-pressure can help overcome the kinetic barrier between hcp and fcc HEAs. Since the hcp CoCrFeMnNi HEA is more thermodynamically stable than the fcc polymorph at lower temperatures, the hcp phase can be retained after pressure release, and this hcp phase may have excellent mechanical properties at cryogenic temperatures.

The polymorphic transition discovered in this work is by no means limited to this specific CoCrFeMnNi HEA, and we expect that this behaviour could be general in various HEAs at certain pressure and temperature conditions. Therefore, our results contribute to understanding of thermodynamics and kinetics in HEA systems. Moreover, the relative stability of the fcc and hcp phases of hard spheres is a long-standing problem in statistical physics. Since the fcc and hcp have identical packing densities and close free energy, the transition between fcc and hcp is believed to be entropy dominated. Therefore, the fcc-hcp transition in HEAs with extremely high entropy could provide ideal model systems for understanding fundamental questions about fcc and hcp packing46. Furthermore, we noticed that both the fcc and hcp can coexist over a wide pressure range (∼22 to ∼41 GPa), which could be attributed to the very similar free energy of the fcc and hcp phases and/or the large energy barrier between them. Decompression from different maximum pressures between ∼22 and ∼41 GPa in our repeated experiments successfully obtains fcc/hcp composites with tunable fractions after pressure release. As recently reported, the fcc-hcp dual-phase Fe50Mn30Co10Cr10 composites, which undergo a strain-induced martensitic transformation of the initial fcc phase, exhibits outstanding mechanical properties that are much better than its monolithic counterpart15. However, no such dual phase composite has ever been observed in an equiatomic multicomponent HEA system with maximization entropy. According to the stability curve established in this work, the transition pressure could be largely decreased at cryogenic temperatures. Therefore, our results suggest new avenues for tailoring HEAs properties in their near infinite compositional space for novel applications via polymorphic transition-induced HEA composites.

Methods

Sample preparation

The polycrystalline CoCrFeMnNi HEA in our work was synthesized by a previously reported gas-atomization method34. Alloy ingots with a nominal composition of Co20Cr20Fe20Mn20Ni20 were melted in an induction-heated vacuum furnace. The melt was then injected through a ceramic tube into the atomization chamber filled with high purity Ar gas. The atomization pressure was set at 4 MPa. The melt droplets cooled down and solidified into powder. The powder was then collected and sieved.

Microstructure and chemistry characterization

The composition of the gas-atomized powder was analysed with a titration method, and the oxygen content of the powder was determined by a fusion method on a Leco O/N analyser. The microstructure of the as-atomized specimens was characterized using a Zeiss Supra 55 scanning electron microscope operated at 15 kV with an energy dispersive spectrometer.

In situ high-pressure synchrotron XRD at room temperature

In situ high-pressure angle-dispersive XRD experiments were mainly performed at the beamline 13-ID-D, Advanced photon source (APS), Argonne National Laboratory (ANL). A monochromatic X-ray beam with a wavelength of 0.2952 Å was focused by a Kirkpatrick-Baez (KB) mirror system down to approximately 2.5 × 4 μm2, in a rectangular shape at the rotation centre of the sample stage. The detector position and orientation were calibrated using the LaB6 standard. High-pressure was generated using a symmetric DAC with a 400 μm diameter culet. The gasket was T301 stainless steel that was pre-indented down to a thickness of ∼42 μm. A 180 μm hole was drilled as the sample chamber by a laser drilling system at the centre of the gasket indention. A few polycrystalline CoCrFeMnNi balls with a diameter of approximately 20 μm were selected and loaded into the DAC, along with a tiny ruby ball beside the samples to calibrate pressure. Helium was loaded into the DAC at sector 13, APS, ANL, as the hydrostatic pressure-transmitting medium. Figure 1b shows the image of the sample with helium loaded at 0.4 GPa. The pressure fluctuation estimated before and after each exposure was found to be less than 0.2 GPa. The background scattering was collected at each pressure by shining the X-ray beam on the empty area inside the sample chamber, which only passed through helium and two diamond anvils. Two-dimensional (2D) diffraction images were collected with a Mar165 charge-coupled device detector (pixel size: 79 × 79 μm2) and the exposure time was set at 2 s. One-dimensional (1D) XRD patterns were obtained by integrating the 2D images along the azimuth angle from 0° to 360° with Dioptas software47. The resulting diffraction patterns were refined via Le Bail refinement using the GSAS package35.

In situ resistive/laser heating XRD at different pressures

To check the structural stability of the CoCrFeMnNi HEA hcp phase, in situ heating XRD experiments were conducted. Resistive heating up to 723 K in a DAC was performed on the high-pressure recovered hcp HEA sample at the beamline 12.2.2 of the Advanced Light Source, Lawrence Berkeley National Laboratory. The hcp-structured CoCrFeMnNi HEA for the heating experiment was synthesized by compressing the original fcc-structured CoCrFeMnNi HEA to 35 GPa and then decompressing it to ambient pressure in a DAC at room temperature. The wavelength of the X-ray was ∼0.4959 Å, and the beam size was 20 × 20 μm2. 2D XRD images were collected using a Mar345 image plate. To achieve higher temperatures and study the stability the hcp phase at higher pressures, a complementary online laser heating system coupled with DACs at the beamline 13-ID-D, APS, ANL was employed to perform double-sided laser heating on the hcp phased sample48. The wavelength of the X-ray was ∼0.3220 Å. NaCl was used as the pressure-transmitting medium, pressure standard and thermal insulator layers. Three pressure points of 6, 14 and 26 GPa were tested. Temperatures were determined by fitting the blackbody radiation spectra of the heated sample on both sides to the Planck radiation function.

Data availability

The data that support the findings of this study are available from the corresponding authors upon request.

Additional information

How to cite this article: Zhang, F. et al. Polymorphism in a high-entropy alloy. Nat. Commun. 8, 15687 doi: 10.1038/ncomms15687 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information

Supplementary Figures and Supplementary Table

ncomms15687-s1.pdf (638.4KB, pdf)

Acknowledgments

This research was supported by the National Natural Science Foundation of China (Nos. U1530402, 51531001, 51671018, 51422101, 51271212 and 51371003), 111 Project (B07003), International S&T Cooperation Program of China (2015DFG52600) and the Program for Changjiang Scholars and Innovative Research Team in University (IRT_14R05). We would like to thank Dr Hongwei Sheng, Dr Sergey N. Tkachev, Rich Ferry, Xiehang Chen and Songyi Chen for their fruitful discussions and kind help. Use of the beamline 13-ID-D (GeoSoilEnviroCARS) was supported by the National Science Foundation (NSF)-Earth Sciences (EAR-1128799) and Department of Energy (DOE)-GeoSciences (DE-FG02-94ER14466). Use of the gas loading system at sector 13 was supported by COMPRES (EAR 11-57758), NSF (EAR-1128799) and DOE (DE-FG02-94ER14466). Portions of the XRD experiments were carried out at the beamline 1-ID-C, APS, ANL. APS is supported by the DOE Office of Science (DE-AC02-06CH11357). The resistive heating XRD experiment was carried out at beamline 12.2.2, Advanced Light Source (ALS). ALS is supported by the Director, Office of Science, DOE-BES under Contract No. DE-AC02-05CH11231.

Footnotes

The authors declare no competing financial interests.

Author contributions Z.P.L., Q.S.Z. and Y.W. initiated this research project. Q.S.Z. and Z.P.L. designed the experiments. F.Z., H.B.L. and Y.L. synthesized and characterized the initial sample. F.Z., H.B.L., Z.D.Z. V.B.P., E.G., J.Y.Y., J.S.O. and Q.S.Z. performed the synchrotron radiation x-ray experiments. F.Z., H.B.L., Z.D.Z., Y.R., X.L. and Q.S.Z. analysed the data. Q.S.Z., Z.P.L., Y.W. and F.Z. wrote the paper. All authors participated in the discussion and interpretation of the results.

References

  1. Moulton B. & Zaworotko M. J. From molecules to crystal engineering:  supramolecular isomerism and polymorphism in network solids. Chem. Rev. 101, 1629–1658 (2001). [DOI] [PubMed] [Google Scholar]
  2. Falini G., Albeck S., Weiner S. & Addadi L. Control of aragonite or calcite polymorphism by mollusk shell macromolecules. Science 271, 67–69 (1996). [Google Scholar]
  3. Dodony I., Posfal M. & Buseck P. R. Structural relationship between pyrite and marcasite. Am. Mineral. 81, 119–125 (1996). [Google Scholar]
  4. Schmokel M. S. et al. Atomic properties and chemical bonding in the pyrite and marcasite polymorphs of FeS2: a combined experimental and theoretical electron density study. Chem. Sci. 5, 1408–1421 (2014). [Google Scholar]
  5. Bridgman P. W. High pressure polymorphism of iron. J. Appl. Phys. 27, 659–659 (1956). [Google Scholar]
  6. Akahama Y., Nishimura M., Kinoshita K., Kawamura H. & Ohishi Y. Evidence of a fcc-hcp transition in aluminum at multimegabar pressure. Phys. Rev. Lett. 96, 045505 (2006). [DOI] [PubMed] [Google Scholar]
  7. Ding Y. et al. Structural phase transition of vanadium at 69 GPa. Phys. Rev. Lett. 98, 085502 (2007). [DOI] [PubMed] [Google Scholar]
  8. Mao H. K., Bassett W. A. & Takahashi T. Effect of pressure on crystal structure and lattice parameters of iron up to 300 kbar. J. Appl. Phys. 38, 272–276 (1967). [Google Scholar]
  9. Sheng H. W. et al. Polyamorphism in a metallic glass. Nat. Mater. 6, 192–197 (2007). [DOI] [PubMed] [Google Scholar]
  10. Poole P. H., Grande T., Angell C. A. & McMillan P. F. Polymorphic phase transitions in liquids and glasses. Science 275, 322–323 (1997). [Google Scholar]
  11. Zeng Q. S. et al. Origin of pressure-induced polyamorphism in Ce75Al25 metallic glass. Phys. Rev. Lett. 104, 105702 (2010). [DOI] [PubMed] [Google Scholar]
  12. Cantor B., Chang I. T. H., Knight P. & Vincent A. J. B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 375–377, 213–218 (2004). [Google Scholar]
  13. Yeh J. W. et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303 (2004). [Google Scholar]
  14. Rost C. M. et al. Entropy-stabilized oxides. Nat. Commun. 6, 8485 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Li Z., Pradeep K. G., Deng Y., Raabe D. & Tasan C. C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 534, 227–230 (2016). [DOI] [PubMed] [Google Scholar]
  16. Koželj P. et al. Discovery of a superconducting high-entropy alloy. Phys. Rev. Lett. 113, 107001 (2014). [DOI] [PubMed] [Google Scholar]
  17. Zou Y., Ma H. & Spolenak R. Ultrastrong ductile and stable high-entropy alloys at small scales. Nat. Commun. 6, 7748 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Zhang Z. et al. Nanoscale origins of the damage tolerance of the high-entropy alloy CrMnFeCoNi. Nat. Commun. 6, 10143 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gludovatz B. et al. A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158 (2014). [DOI] [PubMed] [Google Scholar]
  20. He J. Y. et al. A precipitation-hardened high-entropy alloy with outstanding tensile properties. Acta Mater. 102, 187–196 (2016). [Google Scholar]
  21. Zhang Y. et al. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93 (2014). [Google Scholar]
  22. Otto F. et al. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 61, 5743–5755 (2013). [Google Scholar]
  23. Gali A. & George E. P. Tensile properties of high- and medium-entropy alloys. Intermetallics 39, 74–78 (2013). [Google Scholar]
  24. Tsai K. Y., Tsai M. H. & Yeh J. W. Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. Acta Mater. 61, 4887–4897 (2013). [Google Scholar]
  25. Liu W. H., Wu Y., He J. Y., Nieh T. G. & Lu Z. P. Grain growth and the Hall–Petch relationship in a high-entropy FeCrNiCoMn alloy. Scripta Mater. 68, 526–529 (2013). [Google Scholar]
  26. Schuh B. et al. Mechanical properties, microstructure and thermal stability of a nanocrystalline CoCrFeMnNi high-entropy alloy after severe plastic deformation. Acta Mater. 96, 258–268 (2015). [Google Scholar]
  27. Otto F. et al. Decomposition of the single-phase high-entropy alloy CrMnFeCoNi after prolonged anneals at intermediate temperatures. Acta Mater. 112, 40–52 (2016). [Google Scholar]
  28. Haglund A., Koehler M., Catoor D., George E. P. & Keppens V. Polycrystalline elastic moduli of a high-entropy alloy at cryogenic temperatures. Intermetallics 58, 62–64 (2015). [Google Scholar]
  29. Tonkov E. Y. & Ponyatovsky E. G. Phase Transformations of Elements Under High Pressure CRC Press (2004). [Google Scholar]
  30. Pickering E. J., Muñoz-Moreno R., Stone H. J. & Jones N. G. Precipitation in the equiatomic high-entropy alloy CrMnFeCoNi. Scripta Mater. 113, 106–109 (2016). [Google Scholar]
  31. Laurent-Brocq M. et al. Insights into the phase diagram of the CrMnFeCoNi high entropy alloy. Acta Mater. 88, 355–365 (2015). [Google Scholar]
  32. Ma D., Grabowski B., Körmann F., Neugebauer J. & Raabe D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 100, 90–97 (2015). [Google Scholar]
  33. Tian F., Varga L. K., Shen J. & Vitos L. Calculating elastic constants in high-entropy alloys using the coherent potential approximation: Current issues and errors. Comput. Mater. Sci. 111, 350–358 (2016). [Google Scholar]
  34. Liu Y. et al. Preparation of superfine-grained high entropy alloy by spark plasma sintering gas atomized powder. Intermetallics 68, 16–22 (2016). [Google Scholar]
  35. Toby B. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 34, 210–213 (2001). [Google Scholar]
  36. Birch F. Elasticity and constitution of the Earth's interior. J. Geophys. Res. 57, 227–286 (1952). [Google Scholar]
  37. Huang S. et al. Temperature dependent stacking fault energy of FeCrCoNiMn high entropy alloy. Scripta Mater. 108, 44–47 (2015). [Google Scholar]
  38. Cantor B. Multicomponent and high entropy alloys. Entropy 16, 4749 (2014). [Google Scholar]
  39. Tolédano P., Krexner G., Prem M., Weber H. P. & Dmitriev V. P. Theory of the martensitic transformation in cobalt. Phys. Rev. B 64, 144104 (2001). [Google Scholar]
  40. Cynn H. et al. Martensitic fcc-to-hcp transformation observed in xenon at high pressure. Phys. Rev. Lett. 86, 4552–4555 (2001). [DOI] [PubMed] [Google Scholar]
  41. Zaddach A. J., Niu C., Koch C. C. & Irving D. L. Mechanical properties and stacking fault energies of NiFeCrCoMn high-entropy alloy. JOM 65, 1780–1789 (2013). [Google Scholar]
  42. Jo M. et al. Theory for plasticity of face-centered cubic metals. Proc. Natl Acad. Sci. USA 111, 6560–6565 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Li W. et al. Generalized stacking fault energy of γ-Fe. Philos. Mag. 96, 524–541 (2016). [Google Scholar]
  44. Chung S.-Y., Kim Y.-M., Kim J.-G. & Kim Y.-J. Multiphase transformation and Ostwald's rule of stages during crystallization of a metal phosphate. Nat. Phys. 5, 68–73 (2009). [Google Scholar]
  45. Kibey S., Liu J. B., Curtis M. J., Johnson D. D. & Sehitoglu H. Effect of nitrogen on generalized stacking fault energy and stacking fault widths in high nitrogen steels. Acta Mater. 54, 2991–3001 (2006). [Google Scholar]
  46. Woodcock L. V. Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures. Nature 385, 141–143 (1997). [Google Scholar]
  47. Prescher C. & Prakapenka V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High Pressure Res. 35, 223–230 (2015). [Google Scholar]
  48. Prakapenka V. B. et al. Advanced flat top laser heating system for high pressure research at GSECARS: application to the melting behavior of germanium. High Pressure Res. 28, 225–235 (2008). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures and Supplementary Table

ncomms15687-s1.pdf (638.4KB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding authors upon request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES