Modelling and simulation of the chondrocyte cell growth, glucose consumption and lactate production within a porous tissue scaffold inside a perfusion bioreactor

Graphical abstract

Abstract

Mathematical and numerical modelling of the tissue culture process in a perfusion bioreactor is able to provide insight into the fluid flow, nutrients and wastes transport, dynamics of the pH value, and the cell growth rate. Knowing the complicated interdependence of these processes is essential for optimizing the culture process for cell growth. This paper presents a resolved scale numerical simulation, which allows one not only to characterize the supply of glucose inside a porous tissue scaffold in a perfusion bioreactor, but also to assess the overall culture condition and predict the cell growth rate. The simulation uses a simplified scaffold that consists of a repeatable unit composed of multiple strands. The simulation results explore some problematic regions inside the simplified scaffold where the concentration of glucose becomes lower than the critical value for the chondrocyte cell viability and the cell growth rate becomes significantly reduced.

1. Introduction

In tissue engineering, the development of the artificial tissues largely depends on the supply of an adequate amount of nutrients, including oxygen and glucose to the cells during the culture process [1]. The in vitro cell culture process inside a bioreactor under dynamic flow conditions has shown significant potential for the development of artificial tissues to replace damaged or injured tissues [1]. During such a dynamic cell culture process, the cells are seeded on artificial three-dimensional (3D) scaffolds constructed of biocompatible polymers which are then placed inside the bioreactor to provide nutrients and flow-induced mechanical stimuli, such as shear stress, to the cells to promote cell growth and tissue generation [2], [3], [4], [5]. Freed et al. found that the growth rate of cartilage cells (chondrocytes) decreased in a static culture process as the cell density increased. The reason for this might be that the increased cell density inside the scaffold decreases the permeability, which in turn limits the supply of glucose and thus chondrocyte growth. For a well-mixed culture condition, however, the regenerated cartilage was capable of resurfacing small joints, e.g., the trapezium bone at the base of a human joint [6]. Among the various bioreactors, perfusion bioreactors are the most promising as compared to other non-perfusion bioreactors [7], [8], [9]. In perfusion-type bioreactors, the fluid is directed to flow through the bioreactor and porous scaffold. Typically the inlet velocity inside the perfusion bioreactor varies between 0.1 and 1 mm/s [10], [11]. The study of Davisson et al. demonstrates the positive effects of perfusion on cartilage growth inside a scaffold [12].

Besides the supply of nutrients to the cells, perfusion bioreactors also play an important role in removing the waste products or products of metabolism, such as CO₂ and lactate in order to retain a viable cell culture condition. The chondrocyte cells during the culture process produce a significant amount of lactate due to the presence of glycolysis [1]. The lactate production rate is also related to the metabolism of oxygen [13]. The metabolism of a single glucose molecule yields two lactic acid molecules. On the other hand, three molecules of oxygen are required to oxidize one lactate molecule [14], [15]. As the glucose consumption rate for chondrocyte cells is substantially higher than the oxygen consumption rate, the oxidation of lactic acid molecules can be ignored and only the production of lactate due to glycolysis was considered to perform the simulation [13]. It was also found that glucose is the main nutrient for the chondrocyte cell to develop the intervertebral disc tissue [16], [17]. Even at high oxygen concentrations, disc cells mainly rely on glycolysis and hence produce lactate [18]. A rising level of lactate can decrease the pH level and hamper the cell growth [1]. Typically the disc cells cannot survive at a pH level lower than 6.0 for an extended period of time [16], [17]. In a similar fashion, chondrocytes exhibit higher metabolic activity if the pH value is greater than 7.0 and even slight changes in the pH level (pH 6.6) are found to retard energy metabolism of the cells [19]. A number of experimental and computational studies have investigated the correlation among nutrient consumption, lactate production and pH value during the culture process [13], [20]. Such studies provide important information on the in vitro cell culture process, e.g., a glucose concentration of 0.3 mM and pH value of 6.8 is considered critical for chondrocyte cell viability [20].

Most of the studies investigate the influence of pH and waste products on the cell culture process to date are limited to the static culture process. However, Zacharof et al. studied the cell growth dynamics of Lactococus lactis inside a stirred-tank bioreactor and found that the growth is highly dependent on the substrate consumption and pH value of the medium [21]. To predict the volumetric cell productivity, Zacharof et al. developed a cell growth model by taking into account the influence of the produced lactate and pH value [21]. Zhou et al. studied the interdependence among oxygen, glucose, lactic acid, and pH value for the cartilage culture process [20]. Their study was performed in static, perfusion and suspended culture systems. The results indicated that the perfusion and suspended culture systems produced a higher cell density than the static culture system. In Zhou et al.’s study, the perfusion was modeled for the medium alone and the flow within the tissue scaffold was not considered. Another major drawback of the aforementioned studies [20], [21] is that they do not consider the influence of the shear stress on the cell growth rate. In the studies of Sacco et al. [4], Nava et al. [11] and Hossain et al. [22] the Monod–Contois cell growth equation was modified to incorporate the influence of the shear stress. On the other hand, the cell growth predicted in those studies [4], [11], [22] does not consider the influence of the lactate production during the culture process. As such, a comprehensive resolved scale simulation of the transport inside a complex porous tissue scaffold with a realistic cell growth model is desirable for improving our understanding of the cell culture process in perfusion bioreactor.

Mathematical and computational modelling of in vitro tissue culture process in perfusion bioreactors is capable of providing the nutrient concentration distribution [13]. The developed mathematical models can be used in the simulation to obtain both the nutrient and waste product distribution. However, performing a resolved-scale simulation is difficult due to the complicated geometry of the scaffold, even though the local fluid velocity in perfusion bioreactors is typically very small. Recently, the multiple relaxation time lattice Boltzmann method (MRT LBM) has become an attractive numerical method for simulating flow and mass transfer with complex boundaries [23]. This method has been used to optimise the bioreactor culture condition and scaffold microarchitecture for the culture process [2], simulate packed bed reactors [24], simulate biofilm growth in a 3D porous media [25], and develop a 3D biofilm growth model applicable to random porous media [26]. The D3Q7 MRT LBM mass transfer model is especially suitable for solving the mass transfer equation for high Peclet number flows [27]. In the perfusion culture process the culture medium is typically water and the molecular diffusivity of the nutrients is a few orders of magnitude lower than the kinematic viscosity of water. Even though the Reynolds number is typically within the creeping flow regime, the Peclet number inside the bioreactor is always a few orders of magnitude higher.

This study presents a resolved-scale simulation of fluid flow and mass transfer through a generic scaffold made from strands with a thin layer of chondrocyte cells attached at the strand surface. Such simple unit scaffolds has been widely used in the literature to analyze the mechanical properties of the scaffolds and regenerated tissue [28], to design porous scaffold microstructure [29] and to predict the cartilage tissue growth [11]. The simulation in the present study investigates the shear stress values, the glucose consumption and lactate generation and the pH values at the surface of the strands. Transport of both glucose and lactate by the fluid flowing through the bioreactor and scaffold are also studied. Finally, the Chondrocyte cell growth rate has been predicted for cartilage tissue regeneration, by adopting a growth model which takes into account the shear stress acting on the cells, glucose consumption, and lactate production.

2. Mathematical model

In the present simulation a simplified scaffold structure, which consists of a single pore- or generic- cell – as shown in Fig. 1, is modelled within a perfusion bioreactor. To perform the simulation and develop the model the following assumptions are made:

• 1.The culture medium or the fluid inside the bioreactor is Newtonian.
• 2.The Reynolds number inside the bioreactor is low and the flow is incompressible. The effect of viscous heat dissipation is neglected.
• 3.A thin layer of chondrocyte cells are assumed to be attached at the surface of the strands.
• 4.The thickness of the chondrocyte cell layers is assumed to be negligibly thin compared to the diameter of the strands. Hence it is assumed that the biochemical reactions, such as the Michaelis–Menten kinetics and Monod growth kinetics, occur only on the surface of the strands. Also, the attached cell layers do not have any influence on the flow field.
• 5.The main component of the nutrient (substrate) is glucose and the main product of the glycolysis is lactate. The concentration distributions of the glucose and lactate are predicted by the model. Other nutrients (i.e., oxygen) are not considered.
• 6.The scaffold strands and attached cell layers are rigid and impermeable to the fluid. No-slip boundary conditions are applied at the strands surface.
• 7.To calculate the cell growth rate, initial stage of the culture process was considered.

Fig. 1.

Geometry of the portion of the tissue scaffold considered by the simulation with strand radius R = 0.46 mm.

2.1. Flow equations

The governing equations for the flow are the continuity and momentum equations, which represent the conservation of mass and momentum, respectively:

$$\frac{{\partial u}_i}{{\partial x}_i}=0$$ (1)

$$\rho \frac{{\partial u}_{\mathrm{i}}}{\partial t}+{\rho u}_j\frac{{\partial u}_i}{{\partial x}_j}=-\frac{\partial p}{{\partial x}_i}+\frac{\partial }{{\partial x}_j}\left(\mu \frac{{\partial u}_i}{{\partial x}_j}\right)$$ (2)

where, u_i are the velocity components, x_i and x_j are the spatial coordinates. The subscripts i and j runs from 1 to 3. The variables u_i, x_i and x_j with the subscripts represents as follows: x₁ = x, x₂ = y, x₃ = z and u₁ = u, u₂ = v, u₃ = w. In Eq. (2), ρ is fluid density, μ is dynamic viscosity and p is pressure. Solving the governing equations numerically yields the velocity and pressure fields. From the velocity information, the viscous stress tensor, τ_ij can be obtained by using the following constitutive relation for a Newtonian fluid:

$${\tau }_{\mathrm{ij}}=\mu \left(\frac{{\partial u}_i}{{\partial x}_j}+\frac{{\partial u}_j}{{\partial x}_i}\right)$$ (3)

2.2. Nutrient transport equations

The governing equation for single phase mass transfer through a single pore of a tissue scaffold is the convection–diffusion equation (CDE)

$$\frac{\partial C_{\sigma }}{\partial t}+u_i\frac{\partial C_{\sigma }}{{\partial x}_i}-\frac{\partial }{{\partial x}_i}\left(D_{\sigma }\frac{\partial C_{\sigma }}{{\partial x}_i}\right)=0$$ (4)

where C_σ and D_σ are the concentration and diffusion coefficient of species σ, i.e., glucose (g) and lactate (l). At the surface of the strand glucose is consumed by the thin layer of cells with the consumption rate, R_g which is assumed to be a function of the local glucose concentration C_g is described by the Michaelis–Menten kinetics,

$$R_{\text{g}}(C_{\text{g}})=\frac{R_{\text{mg}}{C}_{\text{g}}}{K_{\text{mg}}+C_{\text{g}}}$$ (5)

where R_mg and K_mg represent the maximum consumption rate and half-saturation constant of glucose, respectively. The values of all of the model parameters are given in Table 1.

Table 1.

Numerical values of the model par ameters used in the simulations.

Definition	Value	Reference
Inlet glucose concentration, Cg	5.56 mM	[20]
Glucose diffusivity, Dg	1.0 × 10−9 m2/s	[13]
Lactate diffusivity, Dl	1.4 × 10−9 m2/s	[13]
Maximum specific cell growth rate, μmax0	1/(2 × 24 × 3600) 1/s	[4]
Glucose consumption rate, ksg	2.3 g/cm3	[38]
Lactate production rate, ksl	2.3 g/cm3	This work
Glucose maximal consumption rate, Rmg	3.9 × 10−5 kg/(m3s)	[38]
Glucose half saturation constant, Kmg	6.3 × 10−3 kg/m3	[38]
α	0.8761	[4]
β	0.1045	[4]

During the consumption of glucose one molecule of glucose is broken down into two lactic acid molecules. Therefore the production of lactate can be expressed by the following equation:

$$R_{\text{l}}=-2\times R_{\text{g}}$$ (6)

2.3. pH equation

At a lower pH value (pH less than 7) the culture medium becomes acidic. The acidic environment can have an adverse effect on the matrix production and even on the cell viability [14]. The pH of the culture medium depends on the lactic acid concentration [30]. Zhou et al.’s [20] experiment developed the following linear relationship between the pH value and lactate concentration:

$$\text{pH}=7.4-0.0406C(\text{l})$$ (7)

2.4. Cell growth equations

For the cell growth, the Monod growth kinetics has been widely used in the literature, i.e.,

$$\mu \left(C_{\sigma }\right)=\frac{{\mu }_{\text{max}}{C}_{\sigma }}{{\rho }_{\text{c}}{k}_{s\sigma }+C_{\sigma }}$$ (8)

where μ and μ_max are the cell growth rate and the maximum specific growth rate, respectively, ρ_c is the reference cell density and k_sσ is a dimensionless parameter representing the Contois saturation constant of species σ. To account for the mechanical stimuli, Sacco et al. [4] modified Eq. (8) by assuming that the maximum specific growth rate is a linear function of the shear stress induced on the cells, i.e.,

$${\mu }_{\text{max}}={\mu }_{\text{max}0}\left(\alpha +\beta \tau \right)$$ (9)

where μ_max0 is the maximum growth rate in a static condition. In the work of Sacco et al., the values of the parameters α and β were determined from experiments [4].

A cell growth equation that considers the inhibition effect of the lactate and the influence of the pH of the media is given by Zacharof et al. [21],

$$\mu =\frac{\left({\mathrm{\mu }}_{\text{max}}\times C_{\text{g}}\right)\left(k_{\text{sl}}+C_{\text{l}}\right)}{\left(k_{\text{sg}}+C_{\text{g}}\right)\times C_{\text{l}}}$$ (10)

In this equation, C_l represents the concentration of lactate. The k_sg and k_sl are the glucose consumption rate and lactate production rate respectively. In the present study the model has been modified using Sacco et al.’s shear stress dependent maximum specific growth rate, i.e.,

$$\mu \left(\tau ,C_{\sigma }\right)=\frac{\left({\mu }_{\text{max}}\left(\tau \right)\times C_{\text{g}}\right)\left(k_{\text{sl}}+C_{\text{l}}\right)}{\left(k_{\text{sg}}+C_{\text{g}}\right)\times C_{\text{l}}}$$ (11)

In this model, only the beneficial effect of shear stress on cell growth has been included. Further experimental studies are required to validate the model, to determine the shear stress range within which the effect on cell growth remains beneficial.

3. Methods

In this study to perform the numerical simulation, only part of a tissue scaffold has been considered as shown in Fig. 1. It is assumed that the scaffold is made of polystyrene and the geometric integrity of the scaffold remains unchanged during the culture process. The co-ordinate frame is located at the mid-point of the inlet plane. The simplified scaffold consists of two circular strands of radius R aligned in the flow direction. These two strands are located 0.7 R downstream of the inlet plane and the length of each strand is 7.8 R. The overall length of the channel in the streamwise direction (x) is 10 R. At 2.5 R from the inlet plane, two circular strands of radius R are positioned perpendicular to the flow, directly above and below the longitudinal strands as shown in Fig. 1. These two strands will be referred to as the front strands in the following discussion. Similarly at 6.5 R downstream, two more strands are positioned perpendicular to the flow; these two strands will be referred to as the rear strands. The center-to-center distance between the two pairs of strands is 4 R. The width and height of the simplified scaffold is 4 R. Note that only one-half of each strand is included in the solution domain.

In this study the fluid flow and mass transfer simulation has been performed using the D3Q19 and D3Q7 MRT LBM model respectively [27], [31], [32]. The details of the MRT LBM methods used in the present paper can be found in previous study [22] and in Sullivan et al. [24]. The number of nodes used for the simulation was 115 × 46 × 46 in the x, y and z directions, respectively. The grid was uniform with a spatial increment of δx = 0.04 mm and the simulation used a time step of δt = 0.266 ms. The radius of each strand was R = 0.46 mm and the distance between the strands is 2R = 0.92 mm. The distance between the strands is selected based on the information available in the literature [10], [33]. The relaxation parameter value was set to s_v = 1.0 to yield a kinematic viscosity of v = 1 × 10⁻⁶ m²/s. The flow inside the channel was driven by the pressure difference specified between the inlet and outlet planes. The Reynolds number for the simulation was Re_D = 0.21 which models the flow condition inside a typical bioreactor and was calculated using the equation, ${Re}_D=\mathrm{UD}/v$, where U is the bulk velocity at the inlet of the channel. The present simulation considers an inlet bulk velocity of 0.23 mm/s. Periodic boundary conditions were applied at the side, upper and lower walls. An interpolation based bounce-back (IBB) boundary condition was used to implement the no-slip condition on the curved wall of the strand on the uniform mesh [34]. It was assumed that the cells are attached uniformly to the scaffold surface and the thickness of the attached cells is negligible compared with the strand diameter. Hence it was also assumed that the glucose consumption and lactate production due to the biochemical reaction occurs only at the surfaces of the strands.

For the mass transfer simulation, the inlet value of the concentration of glucose (5.56 mM) being convected by the incoming fluid is assumed to be uniform. The concentration boundary condition applied at the side walls was periodic. A zero concentration gradient normal to the boundary surface was implemented at the outlet of the bio-reactor using a general bounce-back scheme proposed by Zhang et al. [35] was adopted. A Michaelis–Menten kinetics reaction was specified at the strand surface. To model the reaction on the surface of the circular strand, the consumption rate, R_σ was calculated at the surface of the strand. The concentration values were specified at the surface of the strands using linear extrapolation based on previous time steps and these values were subsequently used to calculate the value of R_σ, which was then used to calculate the distribution functions following the procedure described in Yoshida et al. [27].

The mass transfer simulation was decoupled from the fluid flow simulation and the velocity field obtained by solving the flow equations was used to simulate the mass transport [24]. The decoupling allowed a different time step of δt = 0.005 ms to be used for the mass transfer simulation. The relaxation parameter value of S_D = 1.963 and 1.949 were used to specify diffusivity values corresponding to glucose, D_g = 1 × 10⁻⁹ m²/s and lactate D_l = 1.4 × 10⁻⁹ m²/s; the corresponding Schmidt numbers were 1000 and 714. Consideration of the Schmidt number in such low Reynolds number flow is important since for high Schmidt numbers convection is dominant relative to diffusion [36]. The Peclet numbers of glucose and lactate were 211 and 151, respectively.

4. Results and discussion

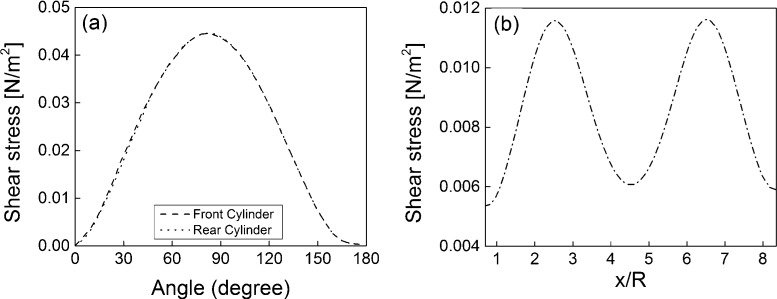
The velocity vector fields on the x–z plane at y/R = 0 and on the x–y plane at z/R = 0, respectively are shown in Fig. 2(a and b) respectively. For a cleaner presentation of the vector field, only one out of two vectors is plotted in the x-direction. Fig. 2(a) indicates that the velocity vector field is symmetric about the center line y/R = 0, as implied by the geometry. The flow is observed to accelerate through the gap between the front strands and a maximum velocity of u/U = 6.76 occur at the center line. The fluid is again seen to accelerate while flowing between the rear strands and a maximum velocity of u/U = 6.80 occur at the center line. No evidence of flow recirculation or reverse flow is evident downstream of the front and rear strands. A lower velocity region is observed between the front and rear strands and behind the rear strands at the top and bottom surfaces of the solution domain. In Fig. 2(b) the velocity vector field is also symmetric about the center line z/R = 0. A relatively high velocity region can be observed from x/R = 1.5 to 3.5 and also from x/R = 5.5 to 7.5. This is due to the acceleration of the fluid flowing between the front and rear strands placed across the flow. The magnitude of the velocity vectors is very low in the region behind the strands near the outlet plane. The surface shear stress profiles are shown in Fig. 3(a) and the profiles are almost identical for both the front and rear strands. The maximum surface stress occurs slightly upstream of the strand shoulder for both the front and rear strands and the value of the maximum shear stress value is 0.04 N/m². The mean shear on the surface of the strand is approximately 0.02 N/m². In Raimondi et al.’s [37] study for an inlet velocity of 0.221 mm/s the mean shear stress was observed 0.016 N/m² inside the bioreactor. The shear stress profile on the inside surface of the strand aligned in the streamwise direction is shown in Fig. 3(b). The value of the shear stress begins to increase at x/R = 1.0 and reaches the maximum value at x/R = 2.5. From x/R = 2.5, the value begins to decrease and the minimum shear stress value occurs at x/R = 4.5. The peaks in the shear stress profile are due to the presence of the front and rear strands with centers located at x/R = 2.5 and x/R = 6.5, respectively. Recall that the acceleration of the velocity vectors associated with the transverse strands was also evident in Fig. 2(b).

Fig. 2.

Velocity vector fields (a) on the xz plane at y/R = 0, and (b) on the xy plane at z/R = 0.

Fig. 3.

Shear stress profiles on (a) the surface of the front and rear strands at y/R = 0, and (b) the strand shoulder along the streamwise direction at z/R = 0.

The steady state glucose concentration distribution on the x–z plane at y/R = 0 and on the x–y plane at z/R = 0 is shown in Fig. 4(a and b), respectively. Fig. 4(a) shows that, the higher glucose concentration, C_g = 5.56 mM, coming from the inlet can only reach up to x/R = 5 or halfway through the pore. At the surface of the strands the concentration values become much lower due to the consumption of glucose by the thin layer of cells. The concentration values are close to zero in the low velocity regions described in Fig. 2a, i.e., between the front and rear strand and behind the rear strand. This clearly indicates that convective transport is important to supply glucose inside the porous structure. Fig. 4(b) shows that along the center line y/R = 0 a relatively high glucose concentration extends up to x/R = 5. A layer of lower concentration values can be observed on the strand surface, and the thickness of the layer increases along the streamwise direction. A region of very low concentration can be seen in the low velocity region behind the strands identified in Fig. 2b. Overall, Fig. 4(a and b) indicate that, for the present flow conditions, the convective transport fails to supply significant amounts of glucose to the region between the front and rear strands, the region behind the rear strands and the region behind the streamwise strands at the exit of the pore. Fig. 5(a and b) show the steady state lactate concentration distribution on the x–z plane at y/R = 0 and on the x–y plane at z/R = 0, respectively. Lactate concentration is higher at the surface of the strands where glucose is consumed. Higher concentration of lactate can also be observed in the lower velocity regions. The lactate contour distributions also indicate that, for the present flow conditions, the fluid velocity is not sufficient to entirely remove the lactate produced at the scaffold surface.

Fig. 4.

Glucose concentration (mM) fields (a) in the xz plane at y/R = 0, and (b) in the xy plane at z/R = 0.

Fig. 5.

Lactate concentration (mM) fields (a) in the xz plane at y/R = 0, and (b) in the xy plane at z/R = 0.

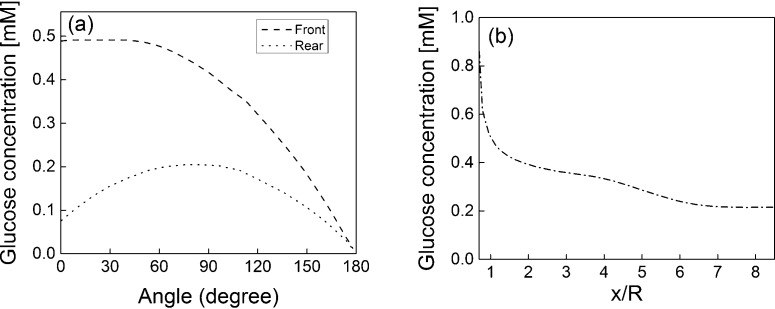
Fig. 6 investigates the glucose concentration on the surface of the strands. Fig. 6(a) shows the glucose concentration profile on both the front and rear strand surfaces at y/R = 0. Recall that the cells were attached to the surface of the strand and that the glucose consumption by the cells is defined by a Michaelis–Menten kinetics-type reaction. The concentration profile for the front strands show that the maximum concentration value occurs near the front stagnation point where the maximum value is approximately C_g = 0.5 mM. The value begins to decrease near 45° and reduces to a value of about C_g = 0.02 mM at the downstream stagnation point. The rear strand concentration profile shows a markedly different behavior than the front strand profile. For the rear strand, the maximum concentration occurs slightly upstream of the strand shoulder and the value is approximately C_g = 0.2. The difference in the maximum glucose concentration between the front and rear strands is approximately 60%, which is significant. From the concentration profiles predicted for the strand surfaces, it is evident that the cells attached to the downstream face of the front strand and to the surface of the rear strands will be supplied with a glucose concentration that is lower than the critical value (0.3 mM). As such, a lower cell growth can be expected for these regions. Fig. 6(b) shows the glucose concentration at the inner surface of the strands aligned in the streamwise direction. A maximum and minimum concentration value can be observed at the front and rear end points, with values of C_g = 0.85 and 0.21, respectively. The concentration of glucose remains higher than the critical value up to approximately x/R = 4.5. In the region from x/R = 4.5 to 8.5, the concentration values fall below the critical value of C_g = 0.3 mM, and hence cell viability is threatened.

Fig. 6.

Glucose concentration profiles on (a) the surface of the front and rear strands at y/R = 0, and (b) the inner shoulder of the strand in the streamwise direction at z/R = 0.

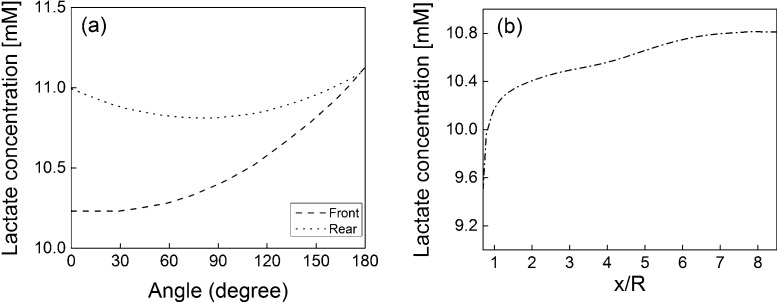
Fig. 7(a) shows the lactate concentration profile on both the front and rear strand surfaces at y/R = 0. The concentration profiles of lactate show the opposite behavior to the glucose profiles. The maximum and minimum values are observed at the downstream and upstream stagnation points, respectively. For the front strand, the minimum concentration value is C_l = 10.25 mM. A maximum value of C_l = 11.20 mM can be observed at the downstream stagnation point. For the rear strand, maximum lactate concentration value is, C_l = 11.20 mM, and can be observed at downstream stagnation point. Fig. 7(b) shows the lactate concentration on the inner surface of the strand aligned in the streamwise direction. The minimum value of C_l = 9.5 mM is found at the front end. The lactate concentration increases along the strand surface as the distance from the front end increases and reaches a maximum value of C_l = 10.8 mM at the rear end point of the strand. The accumulation of lactate inside the scaffold is particularly important as the pH level decreases with increasing lactate concentration. Fig. 8(a) shows the pH profile on both the front and rear strand surfaces at y/R = 0. The minimum pH value of 6.95 occurs at the rear stagnation point for both the front and rear strands, so that the pH value on both surfaces remains above the critical value of 6.8 for cell viability. Fig. 8(b) shows the pH on the inner surface of the strand aligned in the streamwise direction. The minimum pH value of 6.97 occurs at the rear end point of the strand.

Fig. 7.

Lactate concentration profiles on (a) the surface of the front and rear strands at y/R = 0, and (b) the inner shoulder of the strand in the streamwise direction at z/R = 0.

Fig. 8.

pH profiles on (a) the surface of the front and rear strands at y/R = 0, and (b) the inner shoulder of the strand in the streamwise direction at z/R = 0.

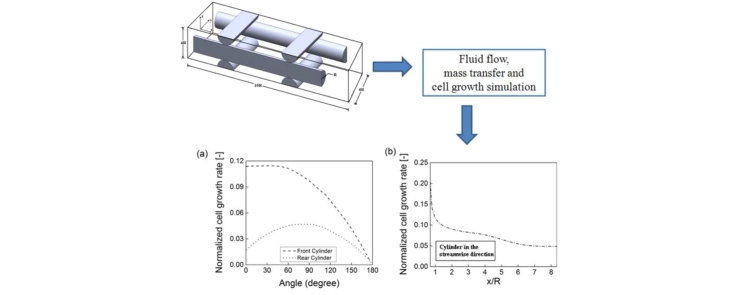
Fig. 9 shows the cell growth rate normalized by maximum specific cell growth rate (μ_max0). Recall that the cell growth rate model adopted in this study (Eq. (10)) considers the shear stress acting on the surface, consumption of glucose and production of lactate. From Fig. 9, it is evident that the cell growth rate profiles show similar behavior as the glucose concentration profiles. This indicates the fact that, the most important factor in cell growth is the glucose supply. The cell growth rate is significantly higher on the upstream face of the front strand where the glucose supply was higher compared to the downstream face. The cell growth rate profile on the rear strand indicates that the maximum cell growth rate occurs at about θ = 75°. In Fig. 9(b), the maximum and minimum normalized cell growth rate is found at the front and rear end, respectively, of the strand aligned in the streamwise direction.

Fig. 9.

Cell growth rate profiles on (a) the surface of the front and rear strands at y/R = 0, and (b) the inner shoulder of the strand in the streamwise direction at z/R = 0.

5. Conclusion

In this study, a resolved scale simulation of the fluid flow and nutrient (glucose) transfer through a simplified tissue scaffold consisting of a repeatable unit/pore inside a perfusion bioreactor has been performed. In this simulation, it is assumed that: (1) the glucose concentration is uniform at the inlet, and (2) the glucose consumption occurred at the surface of the strands by a thin layer of chondrocyte cells following the Michaelis–Menten kinetics. The predictions for the glucose concentration show that at the flow conditions considered in the present study, the value of the glucose concentration becomes lower than the critical value of 0.3 mM on the downstream face of the front strand, on the surface of the rear strand and on the rear half of the inner surface of the strand aligned in the streamwise direction. The major reason for the lower concentration values in the regions described above is the lower velocity which means the convective transport is not high enough to overcome the nutrient consumption by the layer of cells attached on the surface.

The transport of waste products (lactate) through the porous structure has also been included in this simulation. The lactate concentration field shows that a higher lactate accumulation occurs in the regions where velocity is low. However, the decrease in the pH value due to the production of lactate did not fall below the critical pH value required for a viable cell culture condition. The cell growth rate model adopted here considers the influence of shear stress at the surface of the strands, glucose consumption and lactate generation as well as the pH of the culture medium. The maximum cell growth rate occurred at the front region on the surface of the strand aligned in the streamwise direction. The cell growth rates are much lower on the rear surface of the front strand and on the entire surface of the rear strand. The lower cell growth rate in the regions mentioned above is primarily due to the reduced supply of glucose. The influence of the shear stress on the cell growth rate was assumed to be favorable for the present flow conditions.

The simulation results presented in this paper, particularly the detailed information regarding the fluid flow and nutrient transport inside the porous scaffold, would be essential to understanding the perfusion culture process. From the results, it is evident that, to improve the cell growth rate the supply of glucose should be increased inside the scaffold. The existence of regions with a glucose concentration lower than the critical value might not be observed in a volume-averaged analysis. The improvement in the glucose supply can be achieved by increasing the inlet glucose concentration and inlet velocity. However, increasing the inlet velocity will also increase the shear stress levels acting on the cells, so that it would be prudent to first check whether the higher levels of shear stress are within the cell viability range. Increasing the inlet glucose concentration might increase the amount of lactate production due to the higher consumption rate of glucose, which could cause the pH value of the medium to fall below the critical value. As such an optimization would be required to determine the appropriate inlet condition to ensure both an adequate supply of nutrients and favorable shear stress level for promoting cell growth inside the scaffold. The computational framework presented in this study can be a viable tool to obtain the optimal parameters. Increasing the distance between the strands and reducing the diameter of the strands can also increase the transport of glucose inside the scaffold. However, these parameters should be selected through a detail analysis of the scaffold’s mechanical strength. In the future, the authors intend to perform a simulation for a complete porous structure with higher distance between the strands, a higher inlet glucose concentration and flow rate. Such a simulation will be useful for assessing the influence of the higher lactate production and shear stress values on the cell growth rate using the model adopted in the present study.