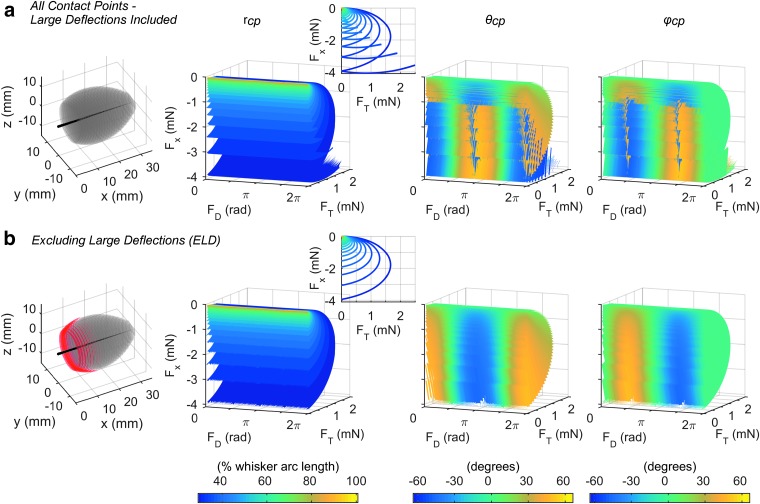
FIG. 6.

The mapping of F_x, F_T, and F_D is not unique for a straight, tapered whisker unless contact points with large deflections are excluded. Color scales are identical for (a) and (b). (a) These four panels show that mappings between F_x, F_T, and F_D and the 3D contact point location (r_cp, θ_cp, φ_cp) are not unique when large angle deflections are included. The first panel shows all 3D contact point locations for a straight, tapered whisker. The whisker is depicted as a tapered, black line, and the gray volume shows all the 3D contact point locations that the whisker was able to reach. Panels 2–4 show the mapping between F_x, F_T, and F_D and r_cp, θ_cp, and φ_cp when all these contact points are included. The panels are color coded for r_cp, θ_cp, and φ_cp, respectively. As in Figure 5, the data points that compose the mappings for all three variables are identical, but their shape appears different because they are constructed of surfaces that slice through the solid differently. The inset to the plot for r_cp shows the mapping projected into the F_x, F_T plane to reveal that the monochromatic surfaces overlap. Overlap is also clearly visible in the mappings for θ_cp, and φ_cp, as seen in the blue appearing to penetrate the yellow. These regions of overlap indicate that the mapping is nonunique and can be more clearly visualized in Supplementary Video S4. (b) These four panels show that mappings between F_x, F_T, and F_D and the 3D contact point location (r_cp, θ_cp, φ_cp) become unique when large angle deflections are excluded. The first panel is identical to the first panel in (a), except that the contact points classified as large deflections are plotted as red dots. Panels 2–4 show the mapping between F_x, F_T, and F_D and r_cp, θ_cp, and φ_cp when the red contact points involving large angle deflections are excluded. The monochromatic surfaces no longer overlap, so the mapping is unique. Supplementary Video S4 shows these mappings rotating in 3D.