Figure A1.

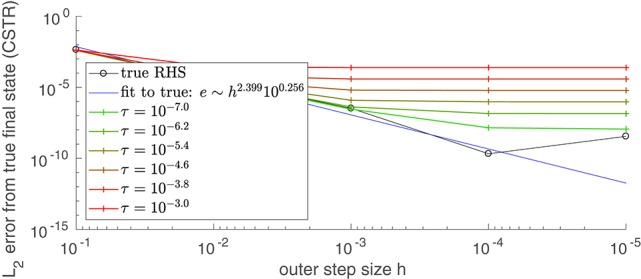
As the inner step size τ decreases, the error (compared to direct integration) of a projective integration becomes bounded instead by the integrator's intrinsic (outer) step size h. Projective integration is performed on a system of two ODEs modeling a single reversible reaction in a continuously-stirred tank reactor with in- and out-flow. Similar to Figure 5, we quantify the difference between direct integration and projective integration, for various values of τ and h. The true solution at t = 0.417 was found by integrating using MATLAB's ode45 with an absolute tolerance of 10^−12.0 and a relative tolerance of 10^−12.0 The series of black circles give the error at t = 0.417 that results from using integration using the true RHS function (Equation 3) in an explicit second-order Runge-Kutta integration scheme of (outer) step size h. The colored curves use the same integrator and outer step size, but approximate the RHS function with a difference map analogous to the coarse difference map of Equation (18). Error is evaluated by taking the 2-norm of the vector difference between the projective integration solution x(0.417) and the true solution.