Significance
Coordinated cell movement is critical for a broad range of multicellular phenomena, including microbial self-organization, embryogenesis, wound healing, and cancer metastasis. Elucidating how these complex behaviors emerge within cell populations is frequently obscured by randomness in individual cell behavior and the multitude of internal and external factors coordinating cells. This work describes a technique of combining fluorescent cell tracking with computational simulations driven by the tracking data to identify cell behaviors contributing to an emergent phenomenon. Application of this technique to the model social bacterium Myxococcus xanthus suggested key aspects of cell coordination during aggregation without complete knowledge of the underlying signaling mechanisms.
Keywords: agent-based simulation, image processing, emergent behavior, fluorescent imaging, cell communication
Abstract
Collective cell movement is critical to the emergent properties of many multicellular systems, including microbial self-organization in biofilms, embryogenesis, wound healing, and cancer metastasis. However, even the best-studied systems lack a complete picture of how diverse physical and chemical cues act upon individual cells to ensure coordinated multicellular behavior. Known for its social developmental cycle, the bacterium Myxococcus xanthus uses coordinated movement to generate three-dimensional aggregates called fruiting bodies. Despite extensive progress in identifying genes controlling fruiting body development, cell behaviors and cell–cell communication mechanisms that mediate aggregation are largely unknown. We developed an approach to examine emergent behaviors that couples fluorescent cell tracking with data-driven models. A unique feature of this approach is the ability to identify cell behaviors affecting the observed aggregation dynamics without full knowledge of the underlying biological mechanisms. The fluorescent cell tracking revealed large deviations in the behavior of individual cells. Our modeling method indicated that decreased cell motility inside the aggregates, a biased walk toward aggregate centroids, and alignment among neighboring cells in a radial direction to the nearest aggregate are behaviors that enhance aggregation dynamics. Our modeling method also revealed that aggregation is generally robust to perturbations in these behaviors and identified possible compensatory mechanisms. The resulting approach of directly combining behavior quantification with data-driven simulations can be applied to more complex systems of collective cell movement without prior knowledge of the cellular machinery and behavioral cues.
Collective cell migration is essential for many developmental processes, including fruiting body development of myxobacteria (1) and Dictyostelium (2), embryonic gastrulation (3, 4), and neural crest development (5). Conversely, cancer cell metastases represent detrimental migratory events that disseminate dysfunctional cells (6). In all these processes, a population of cells leaves its current location and migrates in a coordinated manner to new locations where motility becomes reduced. Remarkable progress has been made in studying the intracellular machinery of these organisms (7). Much less is known about the system-level coordination of cell migration. Cell movement in these systems is a 3D, dynamic process coordinated by a combination of diverse physical and chemical cues acting on the cells (3, 5, 8). Recent developments in tracking individual cell movement in vivo have provided unprecedented detail and revealed surprising levels of heterogeneity (5, 7). Reverse engineering of how these individual cell movements lead to collective migration patterns has proved difficult. Whereas computational models are able to test whether a given set of ad hoc assumptions lead to emergence of observed patterns, these models usually ignore heterogeneity of cell responses, overlook complex behavior dynamics, and rarely perform quantitative comparisons with in vivo results (9–12). Therefore, a data-driven modeling framework that integrates multiple levels of experimental observation with quantitative hypothesis testing is needed to uncover the interactions required for emergent behavior. We explored this possibility, using a simple bacterial model system.
Emergent behaviors are a central feature of the life cycle of Myxococcus xanthus, which occurs within a biofilm many cell layers thick. Cells inside the biofilm are capable of signaling (13) and exchanging outer membrane material (14). Cells are flexible rods that move along their long axis within the biofilm (15). Periodic reversals in direction of movement and a high length-to-diameter aspect ratio allow cells to align with neighbors, move in groups, and follow paths taken by others (16–18). When faced with amino acid limitation, cells self-organize into aggregates much taller than the surrounding biofilm called fruiting bodies (17, 19). Aggregation begins with a burst of cell motility during which cells coalesce into unstable towers a few layers thicker than the surrounding biofilm (20). Within 1 h, towers begin to form spatially stable aggregation centers. Although some aggregates mature into spore-filled fruiting bodies, many initially stable aggregates disseminate back into the biofilm (21). Few data exist on the cues and cell behaviors that lead to these emergent behaviors. Cell-tracking experiments revealed that motility increases outside aggregates (20, 22, 23) and decreases inside (23, 24) whereas statistical image analysis revealed that the area of the aggregate solely determines whether an aggregate will disappear or mature into a fruiting body (19). On their own, these observations have been unsuccessful in explaining how cells coalesce to form stable aggregates.
Biochemical and genetic experiments have identified systems that could play a role in governing cell behavior during aggregation. Cells chemotax toward specific lipids by suppressing reversals when moving up the chemical gradients (25), creating a biased walk. Exopolysaccharides, a major component of the extracellular matrix, also inhibit cell reversals in a concentration-dependent manner (26). However, inhibiting cellular production of known lipid chemoattractants does not diminish aggregation (27, 28), and it is unclear whether exopolysaccharides act as chemoattractants. Induction of developmentally related genes when cells are tightly packed and aligned, but not for randomly positioned cells (29), suggests possible contact-based intercellular signaling. In agreement, cells at low cell densities decrease reversal frequency as group size increases (30). However, this reversal suppression does not directly scale to the cell densities typically used in assays of development (22). Thus, whereas cells undergo behavioral changes indicative of intercellular signaling, conflicting results obscure what these signals are or how they coordinate cell behaviors to drive aggregation. Computational modeling has frequently been used to bypass the lack of specific mechanistic details but has been largely unsuccessful in spanning the realm between fact and fancy.
Although computational approaches have been extensively used in hypothesizing models of aggregation (24, 31–36), the lack of quantitative datasets describing cell movement during aggregation has left the cell behaviors that drive the process conjectural. As a result of these models, cell length-to-width ratio (35), cell alignment (35, 37), active turning (36), density-dependent speed reduction (37), physical jamming (31, 32, 34), and streaming (32, 34) have been introduced as cell behaviors required to generate aggregates in simulations. Quantitative comparisons between simulations and experimental results are needed to evaluate whether these simulations fully capture the characteristics of aggregation, but such comparisons are rarely performed. For example, Zhang et al.’s (21) analysis of the model in which aggregation is driven by cell alignment and reduced cell speed inside aggregates (24) revealed that the simulations fail to quantitatively capture the correct aggregation rate, aggregate distribution, and aggregate count. Despite this wealth of work, neither biological experiments nor mathematical models have so far identified the cell behaviors that mediate aggregation.
Here, in the absence of knowledge about the mechanistic basis of the cues directing cells, we identify motility parameters affecting the emergence of aggregates. We developed an approach that couples multilevel cell tracking (at the level of individual cells within the biofilm and the level of the growing aggregates) with simulations driven by the cell behavior data. Directly including quantified cell behaviors in simulations, rather than averages or artificially generated behavior distributions, allowed full integration of heterogeneity and complex correlations in cell responses. Hypotheses about the cell behaviors driving aggregation were tested in increasingly complex simulations by quantitatively comparing simulations with in vivo results. This iterative process allowed us to identify cell behaviors that are sufficient and necessary to match the observed aggregation dynamics and creates opportunities for more powerful comparisons of mutant/parent behavioral differences in future studies.
Results
Cells Decrease Movement Inside Aggregates.
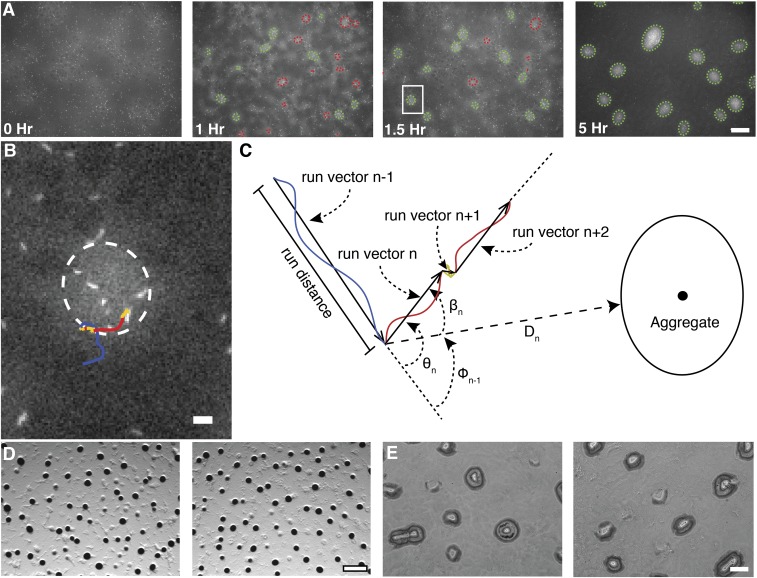
To quantify cell behavior during development, we used time-lapse microcinematography to measure biofilm cell density, determine aggregate boundaries using a cell-density threshold, and follow individual cells within the biofilm (Fig. S1). Under our conditions, aggregation begins 11–12 h after spotting the cells on starvation media. We selected an ∼5-h window that began just before the initiation of aggregation through the period when stable aggregates form (Fig. S1A). The beginning of this window was designated time-point zero. About 1 h into this time span aggregation becomes evident. Stable aggregates appear by 1.5 h with a few of the smaller aggregates disappearing by 5 h. Aggregation was not compromised by the use of strains expressing fluorescent proteins or prolonged fluorescent imaging (Fig. S1 D and E).
Fig. S1.
Overview of individual cell and aggregate tracking. (A) Representative images from time-lapse microcinematography of developing M. xanthus cells highly expressing tdTomato mixed 1:2,500 with cells weakly expressing eYFP. Cell density is proportional to eYFP fluorescence intensity whereas, in the same image, individual tdTomato cells are bright enough to detect and track . Detected aggregate boundaries are indicated with dashed green ellipses for stable aggregates and red ellipses for unstable aggregates. (Scale bar, 100 μm.) (B) Increased magnification of the image area inside the white box in A. Line follows a single cell trajectory from the prior 40 min to the shown frame. Line color indicates detected cell state. Blue is persistent forward, red is persistent backward, and yellow is nonpersistent movement. (Scale bar, 10 μm.) (C) Cell trajectories were segmented into continuous states, and the vector pointing from one state to the next is defined as a run vector. Colors are as in B. Run vector distance, speed, duration, distance to nearest aggregate boundary (), angle between two consecutive run vectors and the angle between the nearest aggregate centroid and the ending of the previous and beginning of the run vectors are representative of the variables calculated. All angles are in the interval [), where (D) Mixtures of LS3629 and LS3908 on plates containing IPTG and vanillate (Left) or DK1622 cells without IPTG or vanillate (Right) produced similar aggregate profiles. Images were taken 48 h poststarvation at 25× magnification. (Scale bar, 500 μm.) (E) Aggregation profiles were similar after 5 h of fluorescent imaging (Left) and without any fluorescent imaging (Right). The phase images were taken at the same time point and magnification as the 5-h panel in A. (Scale bar, 100 μm.)
Cell-tracking algorithms were developed to track individual fluorescent cells over the 5-h window (Fig. S1B). Cell trajectories were subdivided into three movement states: persistent forward, persistent backward, or nonpersistent. A persistent state was assigned to trajectory segments in which cells were actively moving along their long axis. To account for cell reversals, persistent movements were then further classified as backward or forward relative to the direction observed at beginning of the trajectory. The nonpersistent state was assigned when we encountered a velocity too small (less than ∼1 μm/min) or reversal period too high (greater than ∼1 reversal per minute) to accurately detect persistent movement at the spatial and temporal resolution of the time-lapse images. The resulting assignments divide a trajectory into segments. The vector from the beginning of one segment to the next was defined as a run vector (Fig. S1C). As such, a new run begins each time a cell changes its movement state. In what follows, we use run vectors to quantify cell motility behavior and to define the behavior of agents in agent-based simulations.
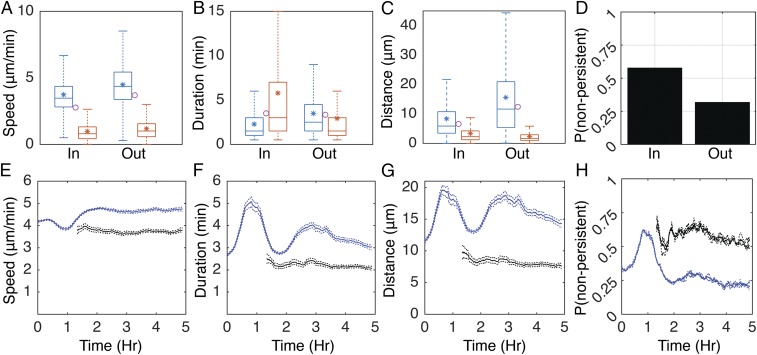
To determine how aggregates affect cell behavior, runs were binned as starting inside or outside the aggregates. In both bins, the speed, duration, and distance of the runs are highly variable (Fig. 1 A–C). Within aggregates, cells move with only a modest average speed decrease of 1.1-fold relative to outside the aggregates (Fig. 1A, blue asterisks). However, the probability for a cell to transition to a nonpersistent state at the end of the run increases 1.8-fold (Fig. 1D). Moreover, the average duration of nonpersistent runs doubles inside the aggregates (Fig. 1B, red asterisks). Average persistent run duration also decreases inside aggregates by ∼1.5-fold (Fig. 1B, blue asterisks). These effects lead to a combined (persistent and nonpersistent) 2-fold decrease in average run distance inside the aggregates vs. outside (Fig. 1C, magenta circles). These results are in agreement with other work suggesting that cells reduce movement inside aggregates (24) and provide much more quantitative detail.
Fig. 1.
Run behaviors are dynamic in time and space. (A–C) Time-integrated distributions of persistent (blue) and nonpersistent (red) run speed (A), duration (B), and distance (C) inside (In) and outside (Out) of the aggregates. Horizontal lines inside the boxes indicate distribution median. Tops and bottoms of each box indicate 75th (q3) and 25th (q1) percentiles, respectively. Whiskers extend to the highest and lowest points or q3 + 1.5(q3 − q1) and q1 − 1.5(q3 − q1), whichever is closer to the median. Asterisks indicate average. Circles indicate combined (persistent and nonpersistent) average. (D) Time-integrated probability of choosing a nonpersistent run after a persistent run inside (In) or outside (Out) of the aggregates. (E and F) Mean (solid lines) and bootstrapped 95% confidence intervals (dashed lines) for run speed (E), duration (F), distance (G), and probability of choosing a nonpersistent run after a persistent run (H) calculated in a 20-min sliding window. Blue lines indicate runs starting outside the aggregates, and black lines, runs inside the aggregates.
Previous observations indicated that cells increase their movement when aggregation initiates (20, 22, 23). To quantify these effects, the mean and 95% confidence intervals for distance, duration, and speed of persistent state runs were calculated in a 20-min sliding window over the length of the experiment (Fig. 1 E–G). Early in aggregation (ca. 0–1.5 h), the mean persistent run duration outside the aggregates increases ∼1.8-fold (Fig. 1F, blue lines), causing an increase in run distance (Fig. 1G, blue lines). At ∼1.5 h, run duration transiently returns to levels seen before the onset of aggregation. Soon after, a second transitory increase in run duration occurs. As aggregates mature, run duration gradually decreases back to preaggregation levels. Inside the aggregates, speed and duration remain constant (Fig. 1 E–G, black lines). Nonpersistent run behaviors are also relatively constant, with run distance varying less than 1.5 µm over the length of the experiment (Fig. S2 A–C). The probability of transitioning to a nonpersistent state remains about the same, with the exception of a transitory increase outside the aggregates coinciding with the first peak in run duration (Fig. 1H). Again, our measurements not only confirm earlier observations but also provide greater quantitative detail to facilitate mathematical modeling.
Fig. S2.
Experimental nonpersistent run behaviors as a function of time. (A–C) Nonpersistent average run (solid lines) speed (A), duration (B), and distance (C) inside (black lines) and outside (blue lines) the aggregates. Average was performed in a 20-min sliding window. Dashed lines indicate 95% confidence intervals.
Density-Dependent Motility Decrease Is Not Sufficient for Aggregation.
To identify the cell behaviors most important to timely and complete aggregation, we developed a data-driven, agent-based simulation technique that couples individual agent behavior with experimentally recorded cell-tracking statistics and biofilm-level dynamics. Agents move in a series of straight lines with properties (persistent vs. nonpersistent, with duration, speed, and turning angle relative to the previous run) sampled from the experimentally measured run distributions. Given that run speed and duration were correlated (Spearman’s for persistent runs, for nonpersistent runs), they were sampled as a pair from a joint distribution containing the values from each experimental run. In the simplest model form, agents choose their run states, speeds, durations, and turning angles randomly from a distribution of all experimentally measured run behaviors independent of their location, cell density, or other factors. Because motility of the agents in this model is uncorrelated with their environment, the model does not generate any aggregates. Cells instead approach a steady state of uniform density (Fig. S3A). For aggregates to form, cells must coordinate their behavior through external cues.
Fig. S3.
Open-loop simulation controls. (A) Comparison of experimental results with simulations in which agents are not dependent on any external variables. Shown are representative time courses of experientially observed (Observed) and simulation (Simulated) cell densities over the course of the experimental time window. (B) Average run distance in a 2-cells/μm2 sliding window for simulations in which agent behavior is dependent on local cell density (blue lines) and experimental results (red lines). Dashed lines indicated bootstrapped 95% mean confidence intervals. (C) Average (solid lines) and SDs (dashed lines) of the percentage of cells inside aggregates for experimental (red lines) and simulations in which agent’s behavior is driven by time since the beginning of the experiment and local cell density (blue lines) or only local cell density (black lines). (D) Average run duration in a 20-min sliding window for all runs (persistent and nonpersistent) from experimental results inside (black lines) and outside aggregates (blue lines) and open-loop simulations in which agent behaviors were chosen dependent on time since the beginning of the experiment. Green lines indicate agents outside aggregates, and red lines, inside. Dashed lines are as in B. (E) Average run distance in a 10-μm sliding window for simulations in which agent behavior depends on orientation to nearest aggregate. Purple (experimental results) and blue (simulation results) lines indicate runs oriented toward [( Fig. S1C] the nearest aggregate centroid. Green (experimental results) and black (simulation results) lines indicate runs pointed away from the nearest aggregate centroid. Negative distances indicate that the run began inside the aggregate. Dashed lines indicated 95% bootstrap confidence intervals. (F) Average (solid lines) and SDs (dashed lines) of the percentage of cells inside observed aggregate boundaries for experimental (red lines) and simulations with a biased walk and with (blue lines) or without (green lines) time since the beginning of the experiment as a dependence for choosing the agent’s run state, speed, and duration. (G) Average (solid lines) and SDs (dashed lines) of percentage of cells inside the aggregates in simulations (black lines) in which agents chose their run state, duration, and speed dependent on orientation and distance to the nearest aggregate when the agent was inside an aggregate (C1) or within 25 μm (C2), 50 μm (C3), or 100 μm (C4) of the aggregate boundary. When outside the cutoff distance (C1–C4), no aggregate dependence was used to choose agent behaviors. Blue lines indicate simulations in which aggregate distance and orientation are always included in choosing agent behaviors. Red lines indicate experimental results.
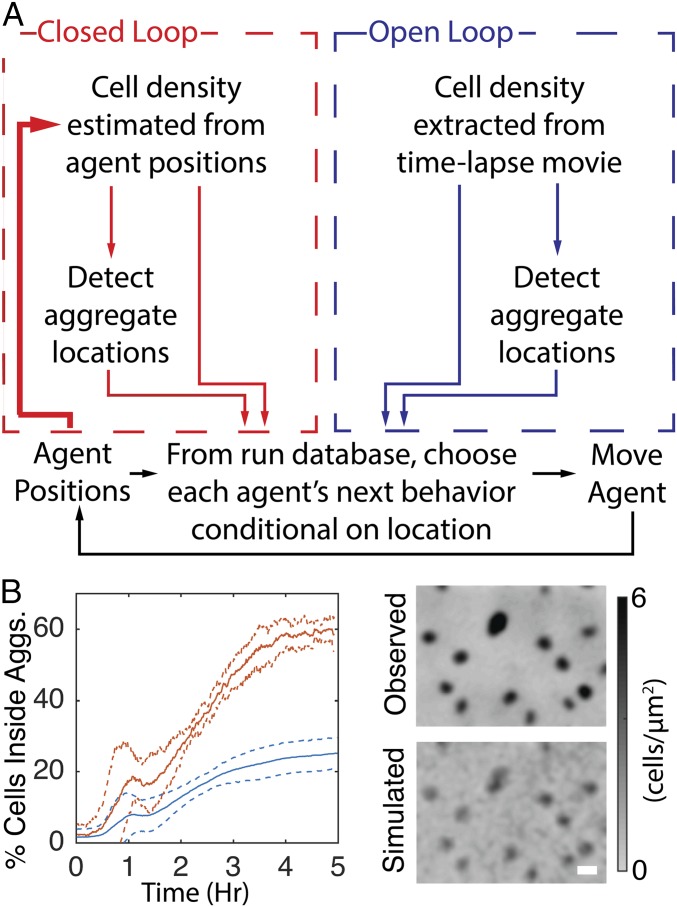
To model behavior dependent on external cues, agent behavior was chosen conditional on the cell density at their location measured in the fluorescent cell microcinematography experiments. As a consequence, agents behave as if they are within the density profiles from the tracking experiments. This technique facilitates directly comparing different cell-behavior dependencies to the experimental results. Varying the enforced run behavior conditions in simulations can then test different hypotheses on the cues coordinating cell behavior. If the correct cell behavior dependencies are included in the simulations, aggregates should appear at the same locations, at the same rate, and to the same extent as the respective movie. We call this simulation type “open loop” to denote that agent behavior is defined solely by the external density profile extracted from a microcinematography experiment (Fig. 2A, blue box).
Fig. 2.
Reduced movement inside aggregates is not sufficient to fully replicate aggregation in open-loop simulations. (A) Overview of open-loop (blue) and closed-loop (red) simulations. The extra path in the closed-loop model is in boldface type to highlight that the agent’s positions feed back into the density profile of the biofilm, closing the loop between individual- and population-level behaviors. (B) Comparison of experimental results with open-loop simulations in which agents reduce average movement proportional to cell density. (B, Left) Average (solid lines) and SDs (dashed lines) of the percentage of cells inside experimentally observed aggregate boundaries for experiment (red) and simulation (blue). (B, Right) Comparison of last frame of representative experientially observed (Observed) cell density with that observed in a simulation.
Previous hypotheses of the mechanistic basis for aggregation predicted that decreased cell movement inside aggregates was the major driver of aggregate growth (21, 24, 31, 32, 38). We tested the hypothesis that the observed decrease in cell movement at the higher cell densities inside aggregates is sufficient to drive aggregation by incorporating density dependence into the simulations. Agents choose their run state, speed, and duration conditional on the experimentally measured local cell density at the beginning of their run. With the addition of this conditionality, agents exhibit a relationship between average run distance and local cell density similar to that of experimental runs (Fig. S3B). In the resulting simulations, aggregates appear at nearly all expected locations (Fig. 2B, Right). However, the fraction of cells within the aggregate boundaries by the end of the 5-h window is threefold smaller in simulations compared with experimental results (Fig. 2B, Left). Addition of time dependence when choosing the state, speed, and duration (Fig. 1 E–H) does not improve the rate or completeness of aggregation in simulations (Fig. S3 C and D). These results are in agreement with another report indicating that simulations driven solely by local cell density fail to correctly reproduce the number, growth rate, and size of aggregates (21).
Cells Perform a Biased Walk Toward the Aggregate Center.
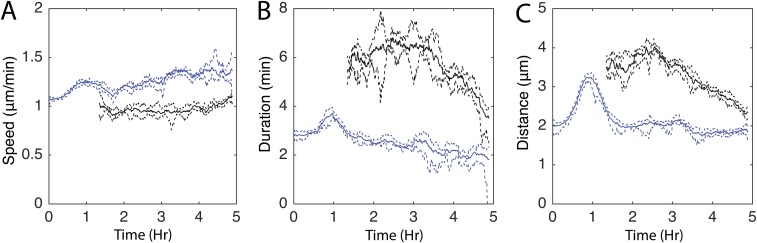
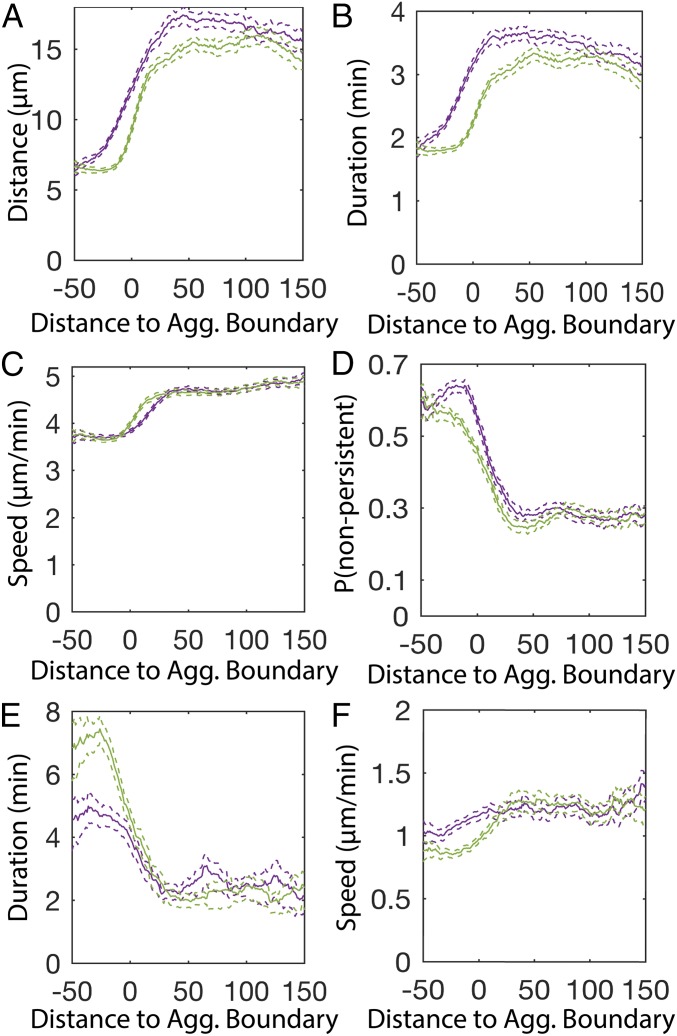
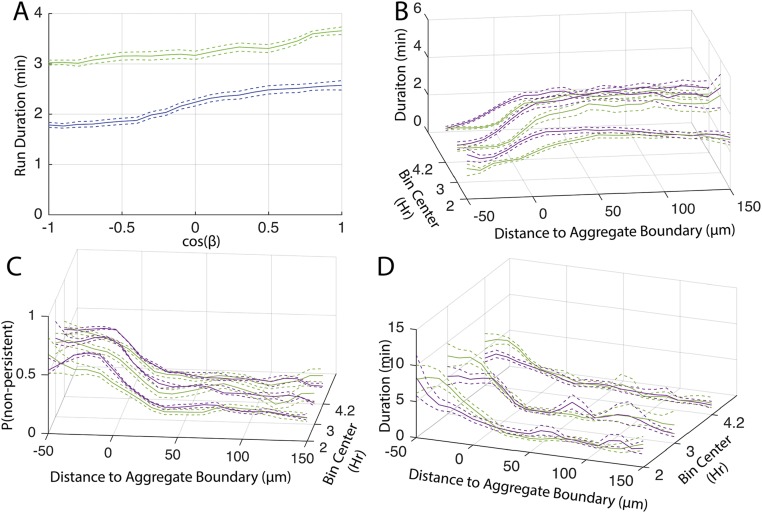
Biased walks are found in many types of cell patterning (8, 39, 40). Although chemotaxis has not been implicated in M. xanthus aggregation, M. xanthus can perform biased walks up specific lipid gradients (25). Bias is created by increasing average run duration when moving up the chemoattractant gradient; conversely, cells decrease average run duration when moving down the gradient. We tested whether cells change their behavior, depending on their direction of movement relative to nearby aggregates. Run vectors were quantified with respect to the direction of moment and distance to the nearest stable aggregate (Fig. S1A, green ovals). The results show that persistent runs moving toward the aggregate centroid are longer than runs moving away from it (Fig. 3A). This bias is due to an increase in run duration rather than run speed (Fig. 3 B and C). The probability of transitioning to a nonpersistent state at the end of the run also depends on the run orientation relative to the nearest aggregate (Fig. 3D). Inside the aggregates, nonpersistent run durations are 1.5 times longer when moving away from the aggregate centroid (Fig. 3 E and F). In contrast to a previous report of tangential cell movement inside the aggregates (41), our run durations are longest when pointed toward the aggregate centroid (Fig. S4A).
Fig. 3.
Cells perform a biased walk toward aggregates. (A–F) Average (solid lines) and bootstrapped 95% confidence intervals (dashed lines) of persistent run distance (A), duration (B), speed (C), probability of choosing a nonpersistent run (D), nonpersistent duration (E), and distance (F) in a 10-μm sliding window from the beginning of the run. Runs are binned into either pointing toward [cos(βn) > 0 in A–C, E, and F or cos(ϕn-1) > 0 in D; Fig. S1C] the nearest aggregate centroid (purple lines) or pointed away [cos(βn) < 0 in A–C, E, and F or cos(ϕn−1) < 0 in D] from the nearest aggregate centroid (green lines). Negative distances indicate that the run began inside the aggregate.
Fig. S4.
Extended biased walk quantification. (A) Average and 95% confidence intervals (dashed lines) of persistent run duration as a function of the orientation to the nearest aggregate centroid (β in Fig. S1C) for runs starting inside (green lines) and outside (blue lines) aggregates. Cos(β) of 1 indicates running directly toward the aggregate centroid and cos(β) of −1 indicates directly away. (B–D) Average and 95% confidence intervals (dashed lines) of persistent run duration (B), probability of choosing a nonpersistent run after a persistent run (C), and nonpersistent run duration (D). Analysis was binned into 1.5- to 2.5-h, 2.5- to 3.4-h, and greater than 3.4-h bins, from front to back, respectively. Purple lines indicate runs oriented toward [ in B and D, in C; Fig. S1C] the nearest aggregate centroid and green lines indicate runs pointed away from the nearest aggregate centroid. Negative distances indicate run began inside the aggregate.
A Biased Walk Toward Aggregates Aids in Aggregation.
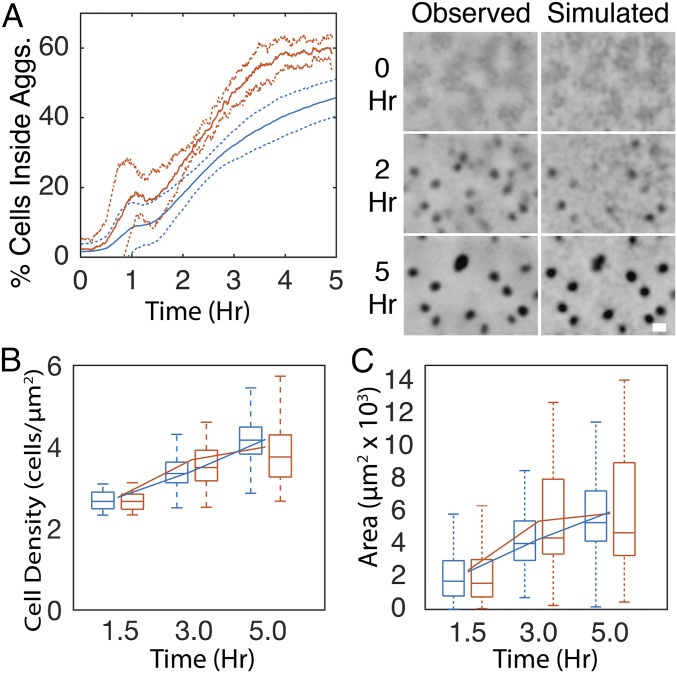
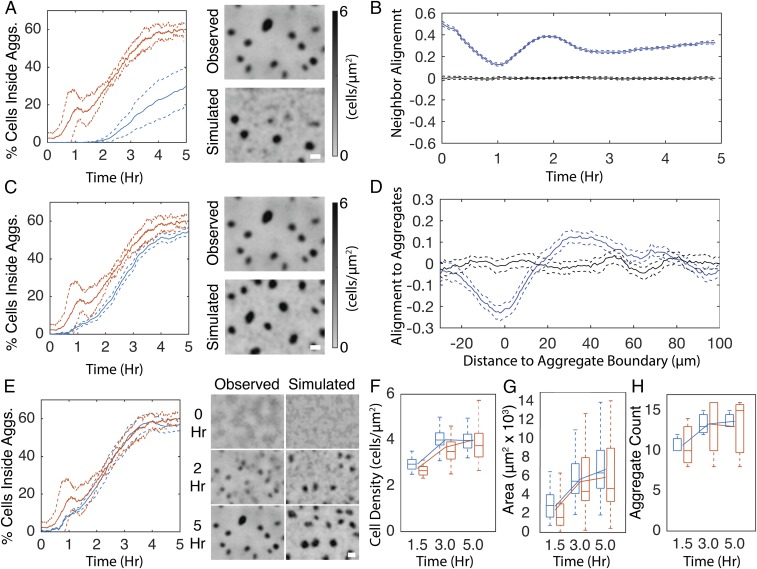
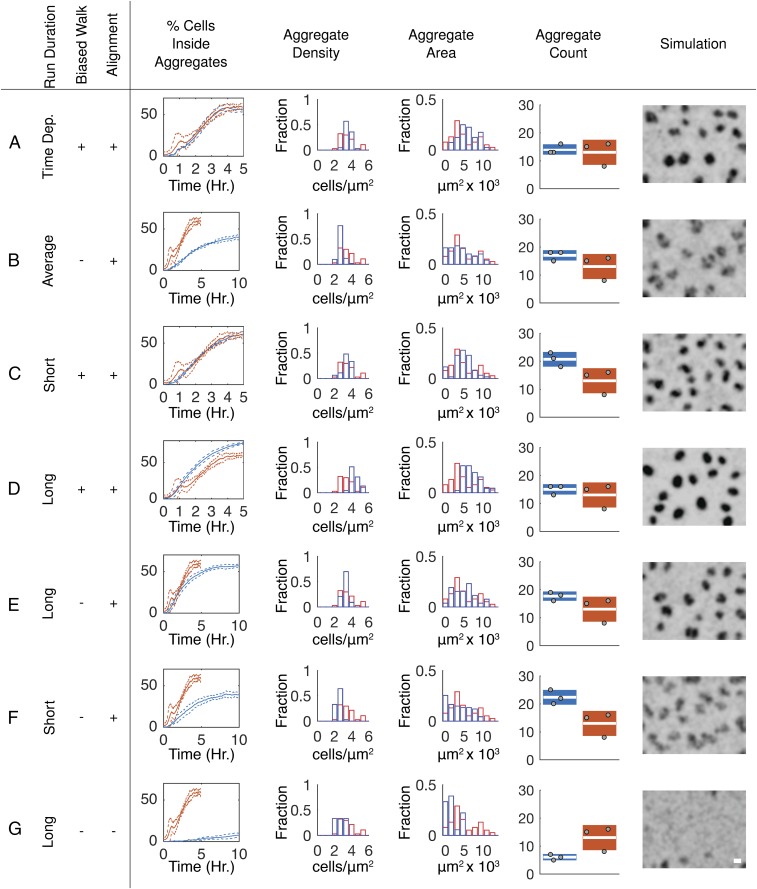
To test the importance of the biased walk in aggregation, simulations were performed in which agent’s run state, duration, and speed were chosen conditional on the orientation and distance of the agent to the nearest aggregate at the beginning of the run in addition to the local cell density. To account for observed time dependence in the biased walk (Fig. S4 B–D), run state, speed, and duration were also chosen conditional on time since the beginning of the experiment. As a result, run duration dynamics relative to aggregate location in the simulation matched those in experiments (Figs. S3E). The inclusion of the biased walk increases aggregation rate and completeness, leading to a twofold increase in the fraction of agents inside aggregates (Fig. 4A). Aggregate density (Fig. 4B) and size (Fig. 4C) in simulations were close to the experimental values. In models with the biased walk, elimination of time dependence in run properties marginally decreases aggregation (Fig. S3F). In these simulations, it is necessary for agents to choose their next behavior conditional on the orientation and distance to the nearest aggregate when up to 100 μm away to achieve full aggregation (Fig. S3G).
Fig. 4.
A biased walk toward aggregates contributes to aggregation in open-loop simulations. (A–C) Comparison of experimental results (red) with simulations (blue) in which agents reduce movement proportional to cell density and perform a biased walk toward aggregates. (A, Left) Formatted as in Fig. 2B. (A, Right) Representative time courses of experientially observed and simulation cell densities over the course of the experimental time window. Grayscale is proportional to cell density as in Fig. 2B. (B) Distribution of average cell density inside aggregates. (C) Distribution of aggregate area. Box plots are formatted as in Fig. 1A. Line plots indicate mean. (Scale bars, 100 μm.)
Closed-Loop Model of Aggregation.
The open-loop simulations identified behaviors that achieve aggregation comparable to that of experimental results. By nature of the technique, aggregate initiation and growth in these simulations were enforced through the continued input of measured cell density profiles. To more stringently test the effect of cell behaviors on aggregation, we closed the loop between agent behavior and the density profile. In contrast to the open-loop simulation’s dependence on experimental cell density profile as input, the closed-loop simulations (Fig. 2A, red box) estimate the density profile from the agent positions by kernel density estimation (KDE) (42). Aggregates were then detected from the agent density profile using the same density cutoff as in experiments. The resulting density profile and aggregate boundaries were used to choose the agent run characteristics, closing the feedback loop between agent behavior and their density profile (Fig. 2A, boldface line). Except for the change in density estimation, the closed-loop model is identical in design to the open-loop model. That is, agents choose their run state, speed, and duration conditional on the local agent density, distance, and orientation to the nearest aggregate and time since the beginning of the experiment. Closed-loop simulations thereby provide a more realistic simulation environment by allowing agents’ positions to modify the surrounding density profile.
The resulting closed-loop simulations lead to aggregate formation but, compared with experimental results and open-loop simulations, the fraction of cells in aggregates decreased about twofold (Fig. 5A). Although the resulting average cell density inside the aggregates agrees with experiments (Fig. S5A), the aggregate area is smaller than in experimental results (Fig. S5B). Therefore, we hypothesized that additional run properties need to be included to facilitate complete aggregation.
Fig. 5.
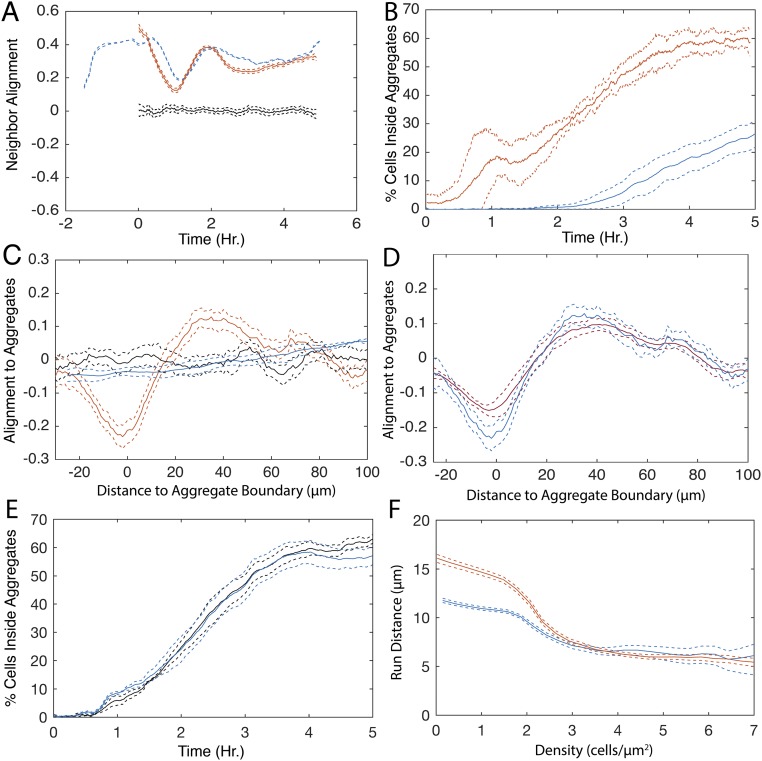
Closed-loop simulations reproduce wild-type–like aggregation with the addition of cell alignment. (A) Simulation results in which agents reduce movement proportional to cell density and perform a biased walk toward aggregates. (A, Left) Average (solid lines) and SD (dashed lines) of the percentage of cells inside detected aggregates for experimental (red) and simulation (blue) replicates. (A, Right) Comparison of the last frame of a representative experientially observed (Observed) cell density with a simulation (Simulated). (B) Average (solid lines) and 95% confidence intervals (dashed lines) of run vector alignment strength (blue lines) with neighboring run vectors that occurred within ±5 min and 15 μm. Black lines indicate alignment strength with randomly chosen runs. Values may span (−1,1) where 1 indicates all runs are parallel. Likewise, −1 indicates all runs are perpendicular. (C) Same as A with the addition that agents in the simulations align their orientation with neighboring agents. (D) Alignment strength of run vectors (blue lines) with vector pointing toward nearest aggregate centroid. Black lines indicate alignment strength after randomly shuffling each run’s distance to the nearest aggregate. Negative distances indicate that the run began inside an aggregate. Values may span (−1,1) as in B. (E–H) In addition to the agent behaviors from simulations in A and C, agents orient toward the nearest aggregate centroid. (E, Left) Percentage of cells inside aggregates as in A. (E, Right) Comparison of representative experientially observed cell density time progression with that observed in the closed-loop simulation. Grayscale is proportional to cell density as in A. (F) Average cell density inside aggregates. (G) Average aggregate area. (H) Aggregate count in each replicate. Box plots are formatted as in Fig. 1A. Lines indicate mean. (Scale bars, 100 μm.)
Fig. S5.
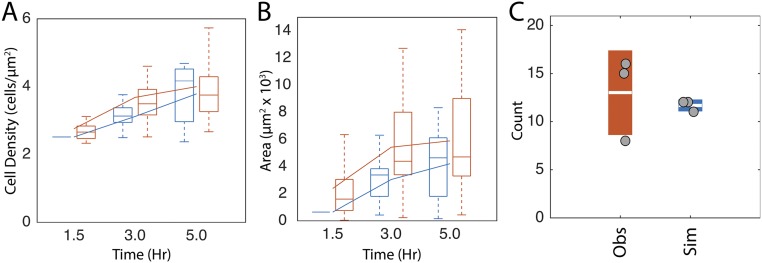
Quantification of closed-loop simulations without agent alignment. (A and B) Distribution of average cell density inside aggregates (A) and aggregate area (B) in closed-loop simulations without any turning angle dependencies (blue lines). Experimental data are in blue. Box plots are formatted as described in Fig. 4. (C) Circles indicate number of aggregates in each experimental movie (Obs) or simulation (Sim). Boxes indicate sample SD with the white line indicating the sample mean.
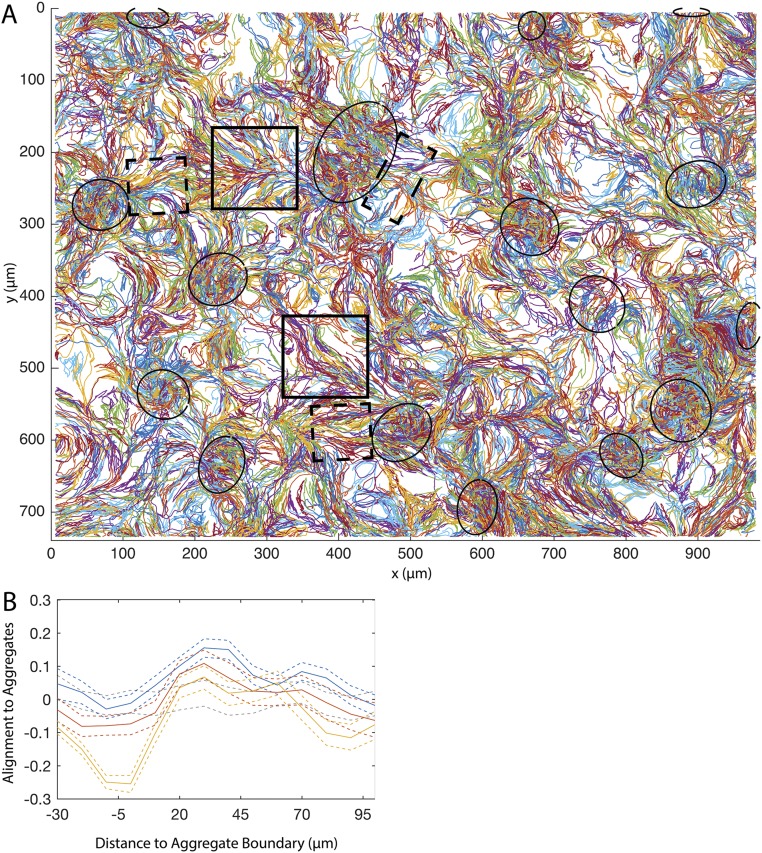
Cell Trajectories Are Aligned Within the Biofilm.
In agreement with other experimental observations (16–18, 23, 24), visual inspection of cell trajectories indicates alignment between neighboring paths (Fig. S6A, solid boxes). The presence of this alignment has previously been proposed to play a role in aggregation, but has not been experimentally quantified in the high cell densities used in developmental assays. To quantify alignment, we followed ref. 16 by calculating nematic alignment strength as the correlation of run orientations modulo 180° (with cells moving in the opposite directions still considered aligned) among runs that start within a 15-µm radius and ±5 min of one another. In agreement with visual observations, quantification indicates a correlation in neighboring run orientations (Fig. 5B). Furthermore, observations (Fig. S6, dashed boxes) and quantification of the mean run orientation relative to the nearest aggregate ( Fig. S1C) indicate that run vectors outside the aggregate preferentially orient in a direction radial to the nearest aggregate (Fig. 5D). Inside the aggregates, runs are biased toward a more tangential orientation. The orientation of cells relative to the aggregates changes with time, with a radial run orientation prevalent at the onset of aggregation and becoming less pronounced as the aggregates mature. In contrast, run orientation inside the aggregates is random early in aggregation and becomes more tangential to the aggregate boundary as the aggregates mature (Fig. S6B).
Fig. S6.
Cell trajectories are aligned. (A) Plot of all cell trajectories extracted from the movie shown in Fig. S1. Trajectories are randomly colored, with colors used multiple times. Ellipses indicate aggregate positions at the end of the experiment. Solid boxes indicate examples of trajectory alignment; dashed boxes indicate examples of trajectories orientated radial to the nearest aggregate boundary. (B) Average alignment strength (solid lines) and 95% confidence intervals (dashed lines) of run vectors with vector pointing to the nearest aggregate centroid during hours 1.5–2.5 (blue lines), hours 2.5–3.4 (red lines), and greater than 3.4 h (yellow lines). Dashed gray lines indicate 95% confidence intervals of alignment strength of a randomly selected set of N runs after randomly shuffling each run’s distance to the nearest aggregate. N was equal to the average number of runs in the time bins.
Cell Alignment Aids in Aggregate Initiation.
The hypothesis that cell alignment improves aggregation was tested in a closed-loop model. Cell alignment was included in simulations by choosing agent turning angles conditional on both the average nematic orientation of neighboring agent runs and the time since the beginning of the experiment. To allow agents time to align before the onset of aggregation, the simulation was run for 1.5 h of simulation time, using the behavior distribution and turning angles from the first 10 min of the experimental results. During this time, agent alignment approaches that seen in the experimental results (Fig. S7A). After the 1.5-h prerun, the simulation was started using agent positions and orientations from the end of the prerun. Addition of neighbor alignment increases aggregation to levels comparable to those of the open-loop model (Fig. 5C). As a control, adding a prerun to simulations without neighbor alignment did not affect aggregation (Fig. S7B), confirming that addition of the prerun does not affect aggregation beyond that of aligning the agents.
Fig. S7.
Closed-loop simulation controls. (A) Time course of mean (solid lines) and 95% bootstrap confidence intervals (dashed lines) of nematic agent alignment with neighboring runs in a 20-min sliding window for simulations (blue) and experimental (red). Negative values indicate the simulation prerun to provide agents time to align. Black lines indicate analysis performed with randomly chosen runs instead of neighboring runs. (B) Average (solid lines) and SD (dashed lines) of the percentage of cells inside aggregates for experimental (red lines) and simulation (blue) with a prerun but no turning angle dependencies. (C) Average (solid lines) and 95% confidence intervals (dashed lines) of mean run vector alignment with vector pointing to the nearest aggregate centroid in open-loop simulations without any turning angle dependencies (blue lines). Black lines indicate a random distribution as in Fig. 5D, and red lines indicate observed experimental alignment. (D) Average (solid lines) and 95% confidence intervals (dashed lines) of orientation of runs relative to the nearest aggregate centroid. Experimental data are in red, and closed-loop simulations in which distance and orientation to nearest aggregate centroid were included as a dependence for choosing turning angle are in blue. The value −1 indicates all runs are tangent to aggregate centroid, and 1 indicates all runs are radial to aggregate centroid. (E) Average (solid lines) and SDs (dashed lines) of fraction of cells inside aggregates in simulations with (blue) and without (black) time as a dependence for choosing the agent’s next turning angle. (F) Average run distance in a 2-cell/μm2 sliding window for all runs (persistent and nonpersistent) that occurred during 1.5–2 h (blue lines) and 2.5–3.4 h (red lines). Dashed lines indicate 95% mean confidence intervals.
The addition of neighbor alignment in simulations does not cause cells to orient radially with the nearest aggregate (Fig. S7C). To include orientation in the simulations, distance to the nearest aggregate boundary and angle to the nearest aggregate centroid were added as dependences on choosing the next turning angle. As a result, the closed-loop model displayed aggregation rates comparable to those of the experimental results (Fig. 5E). Furthermore, aggregate cell density (Fig. 5F), area (Fig. 5G), and aggregate count (Fig. 5H) agree with the experimental results. Thus, the closed-loop model revealed one additional feature not discovered in the open-loop model, a requirement for cell alignment. It now becomes possible to perturb the cell behavior dependences included in the closed-loop model to gauge their relative importance.
Behaviors Shaping Aggregation Dynamics.
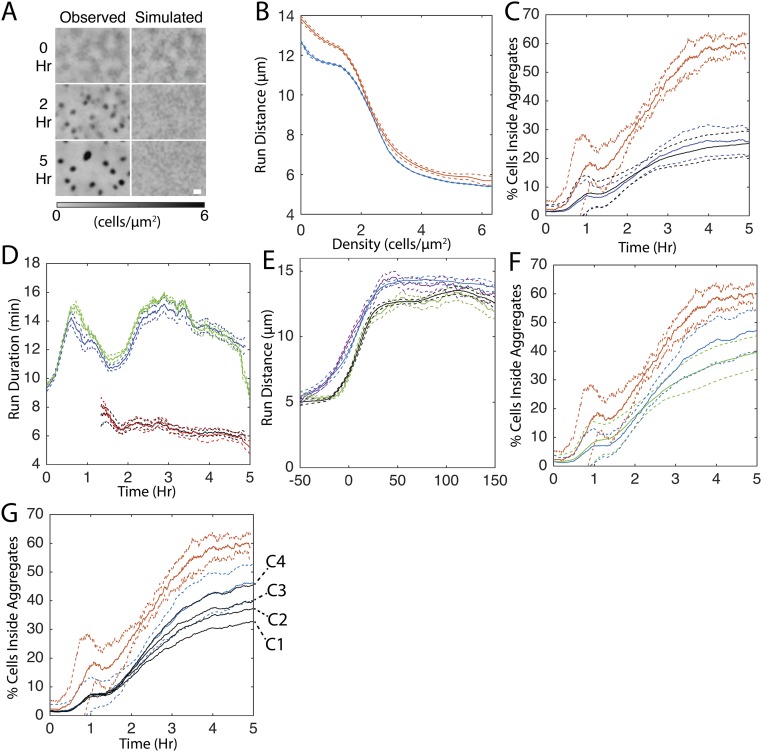
By performing simulations in which the behaviors suggested to be required for aggregation are removed or modified, it is possible to predict phenotypes. To this end, closed-loop simulations were performed in which behaviors identified as necessary to match observed aggregation dynamics were systematically modified (Fig. 6). Time dependence of the agent’s turning angles was not included to enable running simulations for times longer than the available experimental data time window. Simulations indicate that this change does not affect aggregation dynamics (Fig. S7E). As in open-loop simulations (Fig. 2B), removing the biased walk slows the aggregation rate (Fig. 6B). However, by removing the time dependencies, closed-loop simulations can be run beyond the length of the of the time-lapse movies. When simulations were continued for another 5 h, agents continue to aggregate, approaching a steady state by 10 h. Even after 10 h, the fraction of cells inside the aggregates and aggregate density are ∼30% lower than in experimental results and aggregate boundaries appear less well defined.
Fig. 6.
Probing interactions shaping aggregation dynamics in closed-loop simulations. (A–G) Percentage of cells inside aggregates, aggregate area, cell density inside aggregates, and aggregate count from the last time point in simulations (blue) and experimental (red) results. Aggregate density and area box plots are formatted as in Fig. 1. Aggregate count box plots indicate the SD of the replicate counts, white bar indicates the mean count, and each gray dot indicates the count from one replicate. A visual image of the last frame of the simulation was created using a KDE; shading is the same as in Fig. 5A. (Scale bar, 100 μm.) (A) Same simulation as in Fig. 5 E–H. (B) Simulations with run behaviors from the entire experimental time span, alignment to neighboring cells and to the nearest aggregate centroid, and without a biased walk toward aggregates. (C) Simulations with a biased walk, alignment, and run behaviors chosen from a time window (1.5–2 h; Fig. 1F) containing short run durations outside of aggregates. (D) Simulations as in C except run behaviors from a time window (2.5–3.5 h) containing longer run durations outside aggregates. (E) Same as D, minus the biased walk. (F) Same as C, minus the biased walk. (G) Same as E, minus alignment to neighboring runs and the nearest aggregate centroid.
The two transient increases in run duration at the onset of aggregation (ca. 0.5–1.25 h, Fig. 1F) and during rapid aggregate growth (ca. 2.5–3.4 h) suggest a possible role for time-dependent run duration. Outside the aggregates, this increase in duration leads to a combined (persistent and nonpersistent) average run distance in the earlier time window that is 1.3 times longer than in the latter (Fig. S7F). Inside the aggregates, run distances are about the same in both time windows (Fig. S7F). To determine the role of these changes in aggregation dynamics, we used closed-loop models in which run data only from the 1.5- to 2-h or only from the 2.5- to 3.4-h window were used to drive agents’ behavior for the whole simulation duration. Models based on the short run duration window (1.5–2 h) produced aggregates at a rate and completeness equivalent to those of the experimental results (Fig. 6C). In contrast, agents in simulations using the longer run durations (2.5–3.4 h) aggregate at a faster rate and to a higher level of completeness than in experimental results (Fig. 6D). We wondered whether extending the window of longer reversal durations could overcome the need for a biased cell walk. To test this hypothesis, simulations were run using the time windows but without a biased walk toward aggregates. Using the window with longer run durations, agents formed aggregates comparable to those in experimental results in rate, size, and cell density (compare Fig. 6A with 6E). The short run duration window caused agents to aggregate at a rate and completeness comparable to simulations in which behaviors were chosen from the entire movie but without the biased walk (compare Fig. 6B with 6F). Removing both alignment and the biased walk all but abolished aggregation, even when using the longer run duration window (Fig. 6G).
Discussion
Identifying cell behaviors that mediate self-organization without a full understanding of the underlying signaling network and motility control mechanisms is a daunting task. Here we developed a framework that integrates datasets of quantified cell behaviors with computer simulations driven by these datasets to reverse engineer the self-organization process. This approach revealed a set of behaviors that appear to mediate complete aggregation in M. xanthus. Our results suggest that cells use a combination of previously proposed behaviors, such as reduced cell movement inside aggregates, and previously unknown behaviors, including a biased walk toward the aggregate centroid. Remarkably, despite the large heterogeneity observed in individual cell behavior (Fig. 1 A–C), we found that relatively small changes in average cell behavior, such as a 15% increase in average run duration when moving toward aggregates (Fig. 3B), dramatically improved aggregation. At the level of millions of cells, the population can tolerate occasional eccentric behavior provided the average cell behavior engages in the common activity. Live imaging has revealed unexpected heterogeneity and plasticity in stem cell biology (7), suggesting that heterogeneity may be more widespread than currently appreciated in developmental biology. Large deviation occurs at the expense of resource depletion and would be expected to persist only if it provides an evolutionary benefit. The importance of small changes in average behavior in the face of large deviations from the mean also highlights the utility of large experimental datasets and data-driven simulations to confidently distinguish important cell behaviors from background noise.
To uncover the role of each cell behavior in a dataset with multiple correlated and noisy variables, the framework uses two simulation environments (Fig. 2A). The open-loop simulation environment assesses the importance of specific cell behaviors by directly overlaying the simulation agents over experimentally measured environments. This overlay provides a structured way to assess the role of each cell behavior individually. Once the behaviors required to achieve quantitative agreement between open-loop simulations and experimental patterns are identified, closed-loop simulations in which the simulation agents define and modify their environment are used to study how individual cell behavior shapes the behavior of the population. Through systemically adding and removing dependencies driving cell behavior, simulation results predict essentiality of various cell behaviors.
We believe the framework is generally applicable to many types of cell-tracking experiments. The framework can be further generalized to include any additional data on the cell state (e.g., fluorescent gene reporters) or the surrounding environment (e.g., neighboring cells, landmarks, or boundaries) that could be correlated with cell behavior. For example, studies aiming to understand metastatic cancer cell invasion face challenges similar to M. xanthus development. Tumor cell state and migration dynamics are correlated with the local microenvironment, cell genetics, and signaling cues (43). As in M. xanthus development, correlations between these cues and heterogeneity in cell response obscure the relationships between the microenvironment, cell state, and migration. Techniques for individual cell imaging and tracking in tumor models are more complex, but the resulting datasets are similar to that used here. For example, multiphoton microscopy enables tracking of individual cells in vivo and the second and third harmonic generation signals from the technique allow imaging of the environment, including collagen type I fibers, lipids, and lipid bodies, in the same image. Addition of fluorescent dyes, antibodies, and proteins can further enrich the dataset by concurrently providing information about individual cell state, in some cases down to individual signaling pathways (44). Combining the microscopy and cell-tracking data with simulations in which the local microenvironments are defined a priori could be used to identify microenvironment cues of cell behavior that would be analogous to the open-loop simulations described here. In cases where datasets contain a large number of independent variables, or if no clear hypotheses exist, statistical techniques such as correlation analysis, mutual information, or granger causality (45, 46) could be used to generate an initial hypothesis to test in simulations. In systems that have incomplete datasets, hypothesized distributions can be integrated into the agent’s behavior. Modification of what defines an agent in the simulation will be specific to each case, but is straightforward.
Application of the framework to development of M. xanthus identified decreased cell motility inside the aggregates, a biased walk toward aggregate centroids, alignment with neighboring cells, and cell orientation changes with respect to the aggregate boundaries as behaviors contributing to aggregation. Surprisingly, longer run durations outside of aggregates can compensate for lack of a biased walk toward aggregates (Fig. 6E). This observation highlights a possible compensatory mechanism that could make M. xanthus development especially robust. Such compensatory behaviors could mask phenotypes in traditional gene knockout experiments, particularly when relying on visual discriminators such as aggregate area or count at the end of the development. Compensation by modulating run durations is a particularly enticing mechanism because M. xanthus contains 21 chemoreceptors, of which 13 create altered developmental phenotypes when deleted (47), and 2 are thoroughly implicated in both development and reversal control (25, 48, 49). Furthermore, these cell-reversal control pathways can react in timescales of minutes (25) instead of the longer timescales required for protein-level changes. The active role of chemoreceptors in development also suggests the ability to sense chemical gradients, which agrees well with the identification of a biased walk toward aggregates. However, given that no developmental signals have been found yet to guide aggregation, and considering the evidence of contact-mediated reversal control, further studies are needed to unmask the biological mechanisms of the salient cell behaviors.
This approach could speed up physiological analyses of strains containing genetic deficiencies by applying the same framework to analyze the behavior of fluorescently labeled mutant cells. Open- and closed-loop simulations can then be used to test whether behavioral differences observed in mutant cells affect aggregation and predict whether these differences compensate for the lack of another behavior. This approach creates a clear path of combining data acquisition with simulations to formulate hypotheses for future rounds of experiments. In this way, the framework can be used to move from a coarse-grained understanding of the behaviors to a mechanistic understanding of how cellular machinery, signals, and physical integrations guide emergent cell behaviors.
Methods
Bacterial Strains, Plasmids, and Growth Conditions.
All strains and plasmids used in this study are listed in Table S1. M. xanthus strains were grown in CYE broth [1% Bacto casitone (Difco), 0.5% yeast extract (Difco), 10 mM 4-morpholinepropanesulfonic acid (Mops) (pH 7.6), and 0.1% MgSO4] at 32 °C with vigorous shaking. Development was induced on 10 mL TPM agar [10 mM Tris⋅HCl (pH 7.6), 1 mM KH(H2)PO4 (pH 7.6), 10 mM MgSO4, 1.5% agar (Difco)] containing 1 mM isopropyl β-d-1-thiogalactopyranoside (IPTG) and 100 µM vanillate in 100-mm diameter Petri dishes. pLJS145 was constructed by PCR cloning tdTomato from ptdTomato with primers containing 3′-XbaI and 5′-KpnI restriction sites and ligated into pMR3487 (50). pCRC36 was constructed by PCR cloning the eYFP from pEYFP with primers containing 3′-NdeI and 5′-NheI restriction sites and ligated into pMR3629 (50). Strains LS3629 and LS3908 were constructed by electroporation (51) of plasmids pCRC36 and pLJS145, respectively. Following electroporation, transformants were selected on CYE 1.5% agar plates containing 50 µg/mL kanamycin for pCRC36 or 15 µg/mL oxytetracycline for pLJS145.
Table S1.
Strains, plasmids, and primers
| Strains | Description | Source |
| DK1622 | Wild-type strain | (57) |
| LS3908 | DK1622 containing pLJS145 | This study |
| LS3629 | DK1622 containing pCRC29 | This study |
| Plasmids | ||
| pCRC29 | eYFP fluorophore under control of a vanillate-inducible promoter | This study |
| pLJS145 | tdTomato fluorophore under control of an IPTG-inducible promoter | This study |
| pMR3629 | Vanillate-inducible expression vector | (50) |
| pMR3487 | IPTG-inducible expression vector | (50) |
| pEYFP | Clontech | |
| ptdTomato | Courtesy of Roger Y. Tsien, University of California, San Diego, CA | |
| Primers | ||
| eYFP forward | 5′-GTTCTTCATATGGTGAGCAAGGGCGAGG-3′ | This study |
| eYFP reverse | 5′-GTTCTTGCTAGCTTACTTGTACAGCTCGTCCATGCCG-3′ | This study |
| tdTomato forward | 5′-CGTCTAGATGGTGAGCAAGGGCGAGG-3′ | This study |
| tdTomato reverse | 5′-GCGGTACCTTACTTGTACAGCTCGTCC-3′ | This study |
Fluorescence Time-Lapse Image Capture.
Strains LS3908 and LS3629 were grown to exponential phase, mixed 1:2,500 (resulting in ∼500 individually trackable tdTomato cells within the field of view), concentrated to 1.7 × 109 cells/mL, and 35 μL of the cell mixture was spotted onto TPM agar and then dried uncovered in a 32 °C incubator. Once dry, the plates were covered, wrapped with parafilm (Bemis Inc.), and incubated in a heated room. Room temperature varied between 27 °C and 29 °C, averaging 28 °C. Time-lapse images of the spots were acquired using a Leica DM5500B microscope (Leica Microsystems) in the same heated room beginning at the indicated times in the TRITC channel at 200× magnification every 30 s, a short enough time frame that cells do not move more than one cell length between images. Data capture was performed using a Flash2.8 (Hamamatsu Photonics) camera, a Phoenix-D48CL frame grabber (Active Silicon), and the µManager software (52). The fluorescence intensity was set to 55%, camera gain was set to 255, and exposure time was 600 ms. The mercury lamp was shuttered when not acquiring an image. Imaging was carried out for ∼6 h. The time point at which aggregation began varied by up to 1 h between replicates. Replicate movies were truncated to synchronize the onset of aggregation and equalize movie length as described in SI Methods, resulting in final movie length of 5 h. Three replicate movies were created and analyzed in parallel as described below.
Cell Density Estimation.
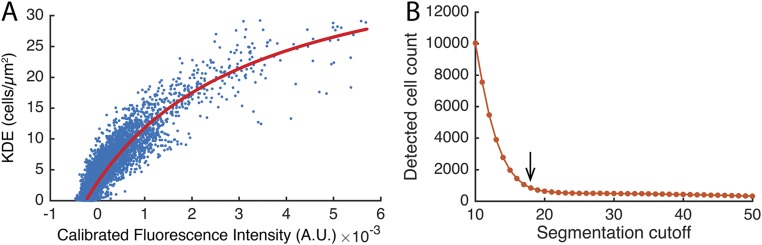
To account for uneven illumination from the microscope’s mercury bulb and optics, acquired fluorescent images were normalized to the intensity of the first frame. Images were then Gaussian smoothed to filter the contribution from the individual labeled LS3908 cells and the images were normalized for diminishing fluorescence over the length of the movie by subtracting the mean intensity of each frame. To estimate cell density, the detected cell positions (as described in Cell Tracking) in the last image from each experimental replicate were used to estimate the cell density, using a kernel density estimator. Comparing the computed cell density with fluorescence intensity values from the last frame indicated a nonlinear correlation between the two (Fig. S8A). To relate these two estimates of cell density (kernel density and fluorescence-intensity density), a third-degree polynomial was fitted to the data pooled from all three movies, using MATLAB’s fit function with the robust option set to Bisquare (Fig. S8A, red line). The fitted polynomial was used to convert fluorescence-density values to cell densities for all images. Further details for the filters and chosen parameters used are provided in SI Methods.
Fig. S8.
Cell density estimation and cell detection parameters. (A) Correlation between individual pixel fluorescence intensity in arbitrary units (A.U.) plotted against cell density estimated using a KDE at the same position as the pixel. Red line indicates the fitted line used to relate the two. (B) Fluorescence intensity cutoff for cell detection was chosen as the bottom of the elbow created when plotting number of cells detected vs. the intensity cutoff. Arrow indicates the cutoff chosen for use in segmentation.
Cell Tracking.
To reduce camera sensor noise and fluorescence from the growing aggregates, time-lapse images were band-pass filtered as described in SI Methods. Thereafter, the MATLAB function regionprops was used to identify the centroid and orientation of each cell. The segmentation threshold value was chosen by running the segmentation and detection on the first image with threshold values between 10 and 50 in 1-unit increments. Plotting the threshold values vs. the number of cells detected (Fig. S8B) indicated that the cell count approaches a constant value as the threshold rises above the noise caused by background fluorescence. Visual inspection of the cell detections indicated a threshold value on the edge of the “elbow” (Fig. S8B, arrow) provided a good tradeoff between detection of all of the cells and little identification of background noise as cells.
To track cell motility between images, we followed procedures established in ref. 53. This technique solves the problem of image-to-image linking of detected cells into trajectories by treating the assignments as a linear assignment problem (LAP). In this method, cells are assumed to move, disappear, or appear between two consecutive images. In the move case, a cell will move to a new position in the time between images. Therefore, its positions in the two images should be linked into the same trajectory. If a cell disappears due to leaving the field of view, misdetection, or overlapping with another cell, it should not be linked to a cell in the later image. In a similar fashion, a cell that appears in the later image should constitute a new trajectory. The LAP involves calculating a cost to assigning each of these actions for every cell in the two images. The resulting costs are then used to find an optimal assignment for each cell by minimizing the total cost of assigning all cells to one of the three options. The process is then repeated consecutively for each image from the time-lapse acquisition. We used the Jonker–Volgenant algorithm (54) implemented in MATLAB by the authors of ref. 53 to solve the LAP (see figure 1 of ref. 53 for an overview of this process). As in ref. 53, a second LAP was then performed to relink broken trajectories. A full definition of the cost functions used for linking cells based on the properties of M. xanthus motility is described in SI Methods.
Cell-State Detection.
Confidently detecting whether a cell is actively moving, stopped, or reversing direction is complicated by noise in the cell trajectories. This noise arises from inaccuracies in detecting the cell position due to the low acquisition magnification and the biological processes that lead to cell movement. We observed that this variability created cell trajectories too noisy for one-dimensional detection techniques (e.g., using tangential speed to detect reversals or a speed cutoff to detect nonmoving cells). To detect movement characteristics of the cell reliably, a cell-state filter was developed that employs extended Kalman filters (EKF) to estimate the most probable motion model used by the cell between images.
We assume cells use the same movement models as described for cell tracking: persistent forward (), persistent backward (), and nonpersistent (). The EKF estimates state vector consisting of the position orientation along the long axis (), and speed () of the cell in image t, using the t − 1 state vector and one of the three movement models (– in Table S2). The EKF then uses the deviation between the predicted state and the true cell state in image t to calculate the likelihood that each movement was executed by the cell. The model with the maximum likelihood was then assigned as the movement between the two images. A detailed description of the movement models and EKF algorithm is provided in SI Methods.
Table S2.
Extended Kalman filter parameters
| Variable | Value | Description |
| Generated from data (Cell-State Movement Models and Detection) | Movement model transition probabilities | |
| Eq. S14 | Process noise covariance matrix | |
| R | (Cell-State Movement Models and Detection) | Measurement noise covariance matrix |
| Initial state | ||
| Forward movement model | ||
| Backward movement model | ||
| Nonpersistent movement model | ||
| Measurement model. Same for forward, backward, and nonpersistent movement models. | ||
| Estimated t + 1 state |
Notation follows that of ref. 58 with the exception of the state vector and measurement vector with cell centroid velocity (), and orientation components at step t.
Aggregate Detection and Tracking.
A cell density cutoff of 2.32 cells/µm2 was chosen by visual inspection of aggregate boundaries in the last image of each movie. Aggregates were detected in each frame as areas where cell density exceeded the cutoff. Aggregate boundaries were approximated as ellipsoids with a centroid, major axis, and minor axis calculated using MATLAB’s regionprops function. To track aggregate positions from image to image, a LAP was set up similar to that used for cell tracking. Adaptions made to track aggregates are provided in SI Methods.
Run Vectors.
Trajectories were divided into runs, which start at the beginning of one contiguous movement state (persistent forward, persistent backward, nonpersistent) and end with the next change of state. Trajectory data before the first reversal and after the last reversal were discarded. The average speed period distance (), angle to the nearest aggregate centroid distance to the nearest aggregate boundary ambient cell density turning angle (), average nematic orientation (explained below) of neighboring runs (), and time since the beginning of the experiment () were calculated for each run vector (Fig. S1C).
Average nematic alignment strength was used to quantify trajectory alignment (Fig. S6A, solid boxes) at the level of a run. The average nematic alignment strength, denoted as is calculated as the average cosine difference between the orientation of run n and all runs within a window size of ±5 min and 15-µm radius around the start of run n:
| [1] |
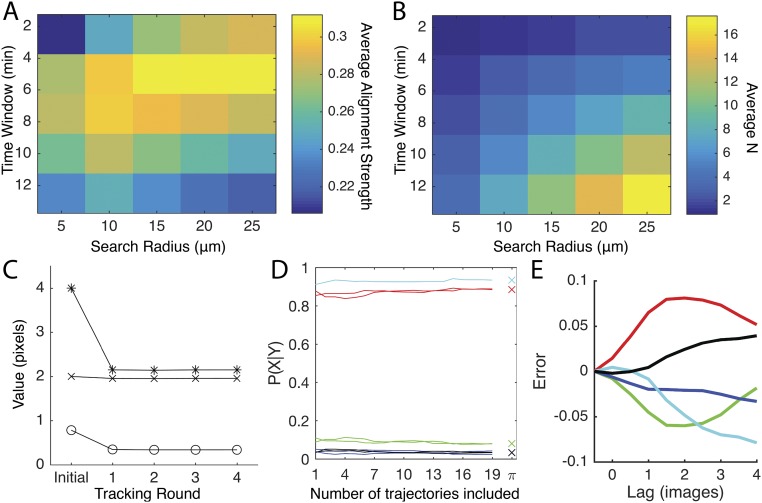
In Eq. 1, N is the number of runs within the window and is the angle of the run relative to the x axis. Due to the lack of motility polarity, the run bearing is in the interval [), where Choosing the window size required balancing an N large enough to reliably evaluate Eq. 1 while avoiding smoothing out local alignment characteristics. Visual inspection of the trajectories indicated that alignment was stable in time (Fig. S6A), allowing the window to be extended in the time dimension to increase N while keeping the spatial search radius around the cell small. The search radius and time-window length were chosen by searching the parameter space of possible values and choosing the combination of values that provided the greatest average alignment strength (Fig. S9 A and B).
Fig. S9.
Cell tracking and quantification parameter estimation. (A and B) Parameter search for alignment window length and size. (A) Mean nematic alignment strength for all runs when calculated using the given time window and search radius. (B) Mean number of runs used to calculate the nematic alignment strength for each run. (C) Progression of variable values for cell tracking calculated using bootstrapping. Asterisks show SD of the difference between predicted and measured cell position open circles show SD of the difference between predicted and measured cell position crosses show mean difference between predicted and measured cell position in x and y directions. (D) Transition probabilities estimated using trajectories from manually assigning trajectory segments as forward, reverse, or nonpersistent movement models. Lines of the same color indicate transition probabilities calculated for forward and backward movement models for continuing persistent movement (red), reversing direction (green), transitioning from nonpersistent to persistent (black), and transitioning from persistent to nonpersistent (blue). Cyan line indicates probability of continuing nonpersistent movement. Crosses indicate values used in transition matrix (E) Error between the transition probabilities estimated using trajectories with manually assigned movement models and that estimated using a Markov chain after a lag of t images. Colors indicate continuing persistent movement (red), reversing direction between the two persistent types (green), transitioning from nonpersistent to persistent (black), transitioning from persistent to nonpersistent (blue), and continuing nonpersistent movement (cyan).
Bootstrapping Statistics.
Where indicated, 95% confidence intervals were calculated by pooling the data from all three replicate movies and bootstrapping parameters using the adjusted percentile method (55) with 1,000 bootstrap samples.
Data-Driven Agent-Based Model.
An agent-based model consisting of 10,000 agents on a rectangular domain of equal to the microscope field of view, with periodic boundary conditions on each end, was implemented in MATLAB. Each agent represents a single cell sampled from a biofilm of the same average density as in experiments (1.1 cells/µm2), similar to sampling cell behaviors in the biofilm using a small number of fluorescently labeled cells. The random trajectory of a single agent consists of the sequence of reversal locations and bearing angles, connected by run vectors and turning angles beginning at time points The run vector is constructed from a run speed and a run duration Because fluorescent images for cell tracking were taken at 30-s intervals, we have adopted the same time discretization in the simulations with agents’ positions along their current run vector updated every The agents’ run variables along with an auxiliary binary variable denoting whether the run is persistent or nonpersistent, are drawn from the reversal probability density function (PDF), where is the time since the beginning of the experiment, is the local cell density, is the angle between the cell orientation and the average bearing angle of neighboring runs, and and are defined in Fig. S1C. We used nearest-neighbor methods (56), to estimate P by drawing a paired (), and from experimentally observed runs conditional on as described in SI Methods. This approach incorporates directly from the experimental run database all of the information available about without relying on an explicit reconstruction of on a high-dimensional variable space.
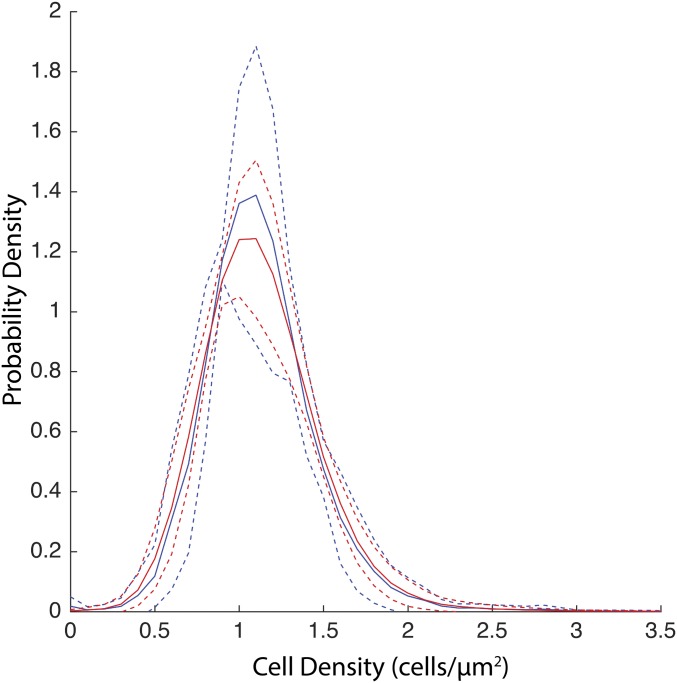
We implemented two alternative modeling approaches, referred to as the open-loop model and the closed-loop model, which differ in how the local cell density () at location and time t was modeled. In the open-loop approach, we used the observed density profile and aggregate locations extracted from each of the three fluorescent and trajectory imaging datasets (movies), as described in Cell Density Estimation. In the closed-loop approach, agent positions were initialized from a uniform random distribution. Each time step, was extracted from the current agent positions with a KDE bandwidth of 14 µm. A 14-µm bandwidth provided good agreement between the starting density distributions of the agents and that measured from experimental results (Fig. S10). Aggregate boundaries and centroids were then calculated from the estimated density profiles, in the same manner as for the experimental imaging density data.
Fig. S10.
Comparison of distribution of biofilm cell densities seen at each (x, y) position within the FOV in the first image of the experimental replicates (blue) or at the beginning of open-loop simulations (red). For experiments, the density was estimated from the fluorescent images. The blue solid lines indicate mean and dashed lines indicate SD of the density distribution from the experimental replicates. For simulations, the (x, y) location of each of the 10,000 agents was drawn from a 2D probability density generated from the density profile of the first image of an experimental movie. The biofilm cell density was then estimated from the agent positions, using a kernel density estimator with a bandwidth of 14 µm. Thirteen simulation distributions were generated per experimental replicate. The red solid lines indicate mean and dashed lines indicate SD of the density distribution from the replicates.
The database of experimentally observed runs used to estimate P can be composed of the composite of all runs extracted from all trajectories tracked across all three microcinematography experiments (three movies) reported here, with = 102,972, or else the database may consist only of the runs from all trajectories tracked in each microcinematography movie, with = 36,019, 36,303, or 30,650, respectively. The composite database was used only for the closed-loop simulations. Each open-loop simulation used only the single-experiment database for the imaging experiment from which also the input cell density profile was extracted.
In open-loop simulations, three independent open-loop simulations were performed for each experimental movie. In the closed loop, three simulations were performed. Each simulation started from a different random initial configuration of agents. The results from the replicate simulations were then pooled for the subsequent data analyses.
SI Methods
Alignment of Experimental Replicate Movies.
The time point at which aggregation began in experiments varied by 1 h between replicates. To normalize for timing variation, the fraction of tdTomato cells inside (cell density >2.32 cells/µm2) the aggregates () was calculated for each image (t) in the movie. These counts were then normalized using
| [S1] |
where N is all images in the experimental replicate. The normalized counts created curves that spanned from 0 before aggregation began to ∼1 after aggregation stabilized. The midpoint of aggregation was identified using the curves by finding the value of that minimized the squared error between the curve and the function
| [S2] |
where is the image time index. To align the replicates, the first frame of the experimental replicate with the minimum was assigned the time point 0. The beginnings of all other replicates were then truncated so that their was equal to the minimum The ends of the aligned replicate were then truncated so that all movies were the same length as the shortest replicate. The final replicate movie length was 590 frames (∼5 h).
Cell Density Estimation.
To account for uneven illumination from the microscope’s mercury bulb and lens optics, acquired fluorescent images were normalized by dividing each pixel intensity by the intensity of the corresponding pixel in a calibration image. The calibration image was created by taking the average intensity for each pixel from the first 15 frames. The resulting image was then smoothed using MATLAB’s (Mathworks, version 2015b) imfilter function with the replicated boundaries option. The mean input filter for imfilter was generated by MATLAB’s fspecial function with a radius of 500 pixels. After the illumination normalization, the images were smoothed using imfilter and an fspecial-generated Gaussian filter with a radius of 30 pixels. This smoothing filtered the contribution from the individual labeled (LS3908) cells in the images. The filtered images were then normalized for diminishing fluorescence over the length of the movie by subtracting the mean intensity of each frame.
To estimate cell density, the detected cell positions (as described below) in the last image from each experimental replicate were used to estimate a probability-density function, using a KDE as described in ref. 42. Version 1.3 of the MATLAB function written by the authors was acquired from the MathWorks File Exchange (File ID: 17204) and modified to allow for a manually set bandwidth of 23.3 This bandwidth was chosen as the average of all three experiments estimated as described in ref. 42. To create a cell density estimate, the probability density function was multiplied by the estimate of the number of cells in the microscope field of view (FOV). Assuming a uniform distribution of cells within the biofilm, a constant number of cells, and that no colony expansion occurs in the experiment, the number of cells was estimated as
| [S3] |
Here the total area was computed as where is the estimated average radius of the five spots measured after drying. The cell density estimate was used to convert the normalized fluorescent intensity values to cell densities as described in the main text.
Bandpass Filter.
A bandpass filter was used to better identify individual fluorescent cells in each frame by removing high-frequency pixel noise from the camera sensor and low-frequency changes in fluorescence due to the growing aggregates. The bandpass filter consisted of separately convoluting the image with a Gaussian with a SD of 10 pixels (∼5 μm, the approximate cell size) and a boxcar function with a width of 1 pixel. To produce the final filtered image, the boxcar-filtered image was subtracted from the Gaussian-filtered image (59).
Cell Tracking.
To track visually indistinguishable cells from image to image, we need to formulate a cost function for linking cells in consecutive frames that relies on the properties of M. xanthus motility. To this end, we assume cells use one of three movement models: persistent forward, persistent backward, or nonpersistent. The cost of using each of the models in the LAP is then calculated by measuring the difference between the detected cell positions ( ) and orientation along the long axis of the cell () and those predicted by the movement models ( ). The predicted positions of each cell are computed from their position in image t as follows:
| [S4] |
Here is a coefficient specific to the movement model and is 1 for forward, −1 for backward, and 0 for nonpersistent movement. For cells that were tracked in the preceding image, are displacements in the previous time interval, i.e.,
| [S5] |
For cells that first appear in the image at time t, the and are estimated based on the orientation of cell major axis and mean-square displacement of all tracked cells as follows:
| [S6] |
Here the angle brackets indicate the average from all cell links assigned in t − 1 to t images. If no trajectories contain a t −1 position, the averages were substituted with an alternate constant chosen using the bootstrapping technique discussed below. The orientation of cells is assumed to vary little between frames and is thus predicted as
The deviations between the measured and predicted cell positions ( and orientations () each make contributions to the cost of linking cells into the same trajectory. By assuming the deviations are independent and normally distributed, the cost is calculated as
| [S7] |
Here
| [S8] |
where atan2 is MATLAB’s four-quadrant inverse tangent function and is Gaussian with 0 mean and SD (58):
| [S9] |
The SDs were calculated using bootstrapping methods discussed below. The cost of linking in Eq. S7 is calculated for each movement model for each cell pair between image t and t + 1. The minimum of the costs among the three movement models is assigned as the cost of linking the cell pair into the same trajectory. The costs associated with a trajectory ending or beginning were calculated as described in ref. 53.
Cells may be misidentified for a short time (one to five images) due to their overlap with another cell or due to segmentation errors. This can lead to the movements of the same cell being split into multiple trajectories. To address this, we again follow the work of ref. 53 and develop a second LAP to connect split trajectories. In this LAP we assume the end of a trajectory could be split due to the errors discussed above or could be a true ending or beginning due to cells entering or leaving the FOV. The cost of assigning the beginning and ending of each trajectory to one of these possibilities was calculated as described below and used in a LAP to find the optimal combination of assignments.
The cost of linking the end of one trajectory with the beginning of another consists of contributions from the distance (), change in cell orientation (), the angle enclosed between the orientation of the cell and a vector connecting (), and the time () between the end of one trajectory and beginning of the other trajectory to be linked. We assume the contributions are independent from each other, allowing the cost to be calculated as
| [S10] |
In Eq. S10, was calculated from a normalized histogram for each length using the previously linked trajectories. The number of bins in the normalized histogram was chosen using the Freedman–Diaconis rule (60). The average gap length was assumed to be 1 and was generated from a Poisson distribution with Only gap lengths ( less than six images were considered for closing.
The cost associated with not linking trajectories together was calculated as in ref. 53. The resulting LAP was solved as discussed previously. Trajectories that spanned less than 5 min (10 consecutive images) were then discarded.
Bootstrapping Unknown Tracking Parameters.
Because few data on the behavior of cells inside the biofilm exist, we bootstrapped the unknown SDs in Eq. S7 and the alternative displacement for Eq. S6 from the tracking itself. This was done iteratively by performing the tracking, calculating the required variables from the results, and then using them in the next round of tracking. Values for the first round of tracking were chosen based on visual inspection of the time-lapse images. These values were radians and pixels for Eq. S9 and 2.5 pixels for the alternative cell displacement used in Eq. S6. For subsequent tracking rounds the values were generated from the trajectories resulting from the previous round. The iterative tracking continued until the deviation between rounds was less than 1%. This convergence required less than five rounds of iteration (Fig. S9C). The values from the fifth round were used in the tracking.
Cell-State Movement Models and Detection.
Given a set of state vectors representing the movement states of a cell up to frame t plus an estimated t + 1 state (), the probability of each movement model () being used between image t − 1 and t can be written as
| [S11] |
Here c is a normalization factor ensuring the probabilities of the three movement models sum up to 1. By assuming the transitions between movement models are reasonably Markovian (Fig. S9D, discussed below), can be approximated recursively (58). Thus, is approximated as
| [S12] |
with transition probabilities whose derivation is discussed below. is approximated using a Markov chain,
| [S13] |
where is estimated by the EKF, using as defined in Table S2. augments the estimation of to include available future cell-state information. For each of the trajectories generated from the cell tracking, the conditional probabilities and cell-state vectors in Eq. S13 were estimated using EKFs (58) with the parameters listed in Table S2 and justified below. If an EKF predicts a movement in the opposite direction from the measurement, it was assigned a probability of 0 for that step. At each step t, the movement model with the maximum probability [ from Eq. S11] is chosen and then used to estimate for the next iteration of the EKFs.
The EKF integrates uncertainty into the model likelihood estimation by adding noise to the movement (– in Table S2) and measurement (h in Table S2) functions. The noise is assumed to be Gaussian with a mean of zero and covariance Q for movement and covariance R for measurement functions. This noise models influences on cell movement not accounted for in the functions. Typically, these would be developed a priori, using an understanding of how the system was measured and how process noise arises. Because few data on the behavior of cells inside the biofilm exist, we instead estimated the covariance matrix Q from the deviations between the predicted ( and measured ( variables from the cell movement tracking (Eq. S4). Q was generated from these deviations as
| [S14] |
Here is the deviation between the predicted and measured t + 1 values that resulted in a linking assignment using model m in the LAP, and angle brackets indicates the mean. The deviation in the cell speed was calculated as
| [S15] |
where is from Eq. S8 and is the time between images. Because Q was calculated directly from the trajectories, which include any measurement noise, the calculation was simplified by setting the measurement covariance (R) to 0. Because forward and reverse models differ only in the direction of the movement, their deviations were pooled to create a single matrix used for both their EKFs.
The transition matrix was generated by manually assigning the movement model for each step from 19 randomly chosen trajectories. was then calculated from these trajectories. Nineteen trajectories were sufficient for the probabilities to stabilize to within ±0.005 per trajectory added (Fig. S9D). We assumed the transitions for persistent forward and backward models were equal. This was asserted by pooling the forward and reverse transition data and calculating one set of transitions for both models (Fig. S9D, crosses). Model transitions were confirmed to be reasonably Markovian by comparing the probability of transitions after a time lag with the Markov chain of the same length with transition probabilities (Fig. S9E).
Aggregate Detection and Tracking.
Aggregates were assumed to keep an approximately constant centroid position (x,y) and major (a) and minor (b) axes between images, deviating only by noise. The cost of linking an aggregate in image t with an aggregate in image t + 1 in the LAP was calculated as the log-likelihood of the deviation between the centroids (), the major (, axis, and the minor ( axis of the two aggregates:
| [S16] |
In Eq. S16 is as in Eq. S9 and the deviations were calculated as
| [S17] |
Because aggregates are reasonably well spaced and move or grow little between images, precise values of were not vital for accurate tracking. Thus, was set to 10 μm and to 25 μm and the resulting trajectories were visually inspected to confirm fidelity.
The stability of the aggregates also allows forgoing the second LAP round used in cell tracking. Instead, aggregates in image t that were not linked to an image in t + 1 were propagated to image t + 1 with the same centroid and major and minor axis. Propagation was allowed to continue for up to five consecutive images. If a propagated aggregate was not linked to a detected aggregate within five images, the trajectory was ended at the last frame the aggregate was detected.
This study focused only on stable aggregates, defined as aggregates that were present at the end of the experiment (compare green and red ellipses in Fig. S1A). Any aggregate that merged into a stable aggregate was also included in the analysis. Merge events were detected as aggregate centroids in image t that ended within the boundaries of another aggregate in image t + 1. All other aggregates that did not fit these criteria were discarded from the analysis.
Data-Driven Agent-Based Model.
The agent positions are updated every using
| [S18] |
Here is the orientation angle of the agent generated from the orientation of the previous run ( and the turning angle of the current run by
| [S19] |
Note that subscript i denotes the current run and is incremented at the end of each run only when an agent chooses new run variables ( and defined below) whereas t denotes simulation time and is incremented at each simulation time step.
The run variables along with an auxiliary binary variable denoting whether the run is persistent or nonpersistent, are drawn from the conditional reversal PDF of the general functional form
| [S20] |
In other words, is assumed to be conditional upon variables and where is the time since the beginning of the experiment, is the local cell density, is the angle between the cell orientation and the average bearing angle of neighboring runs, and and are defined in Fig. S1C. To calculate we introduce the average bearing angle of neighboring runs at the location of the end of run n − 1. is evaluated using the same window as in Eq. 1, using
| [S21] |
where is then the smaller of the two angles between and
Given the above definitions of agent behavior, agent positions for each time step are calculated using the following four steps for each of the 10,000 agents:
Step 1: Simulation initialization.
The agent’s initial position, ( ), is chosen. In closed-loop models, ( ) is drawn uniformly from the rectangular simulation domain. In open-loop models, ( ) is drawn from a 2D probability density generated from from the corresponding experimental movie. The run index is initialized to and a random initial bearing angle is drawn uniformly from the interval [ ).
Step 2: Choose run variables.
In the closed-loop case, the initial density profile, is generated from the positions of all 10,000 agents. In the open-loop case, is the density profile from image t of the respective experiment. is determined for each agent from the agent’s position, is used to determine aggregate locations, if any, including their centroids and boundaries. Angle ( ), and any detected aggregate centroid locations are used to calculate, and In the event that does not yet exhibit any aggregates, and are left undefined. is calculated as described above (Eq. S21 and surrounding text).
Given for run index a random is drawn from using the experimental trajectory-based conditional drawing procedure described below. In cases where and are undefined, due to the absence aggregates in or if no runs have occurred within the last 5 min of simulation time and 15 µm of the agent’s position to calculate their respective conditionalities were not enforced in the experimental trajectory-based drawing procedure. was used to calculate as described in Eq. S19.
Step 3: Advance the simulation.
and were used to calculate using Eq. S18 for time steps to
Step 4: Checking for run termination.
If step 3 was repeated on the next simulation time step. If the run index for that agent was advanced from to ( ) were relabeled as ( ), and step 2 was repeated on the next step. Steps 2–4 were repeated until reached the simulation termination time.
Choosing an agent’s next run behaviors.
For later reference, we need to determine the overall range spanned by the state variables in across the entire database, where for observed runs labeled by with denoting the total number of observed runs in the database. Here and later, the hat () is used to denote variables derived from the microcinematography movies when confusion between microcinematography- and simulation-derived variables may exist. We also explicitly define the angle enclosed between and (Fig. S1C). For nonangular, continuous state variables, these ranges are defined as
| [S22] |
Because angular variables are only defined modulo we restricted each of them to the interval before taking their differences. Subject to that modification, the ranges of the angular state variables are then defined by
| [S23] |
Note that the resulting range values, and are then in fact very close to because the angles whose differences are being maximized typically cover almost their entire allowed range from to
The approach also allows us to incorporate additional, more selective hypotheses about the structure of and test them against the actually observed collective aggregation behavior. In this manner, we can assess in detail whether the real cells are indeed responding significantly to a specific set of hypothesized condition variables and, if so, how strongly. The approach is illustrated below for a relatively simple example of assumed dependencies, without any dependence on nematic alignment. Adapting this technique to other combinations of dependencies is straightforward. The conditionality structure assumed in this example is as follows.
Conditionality hypothesis 1.
The state of motion variable, is conditional upon and can be drawn independently of from a conditional PDF, denoted by of the form
| [S24] |
Conditionality hypothesis 2.
The random reversal angle variable, is conditional upon and can be drawn independently of from a conditional PDF, denoted by of the form
| [S25] |
Conditionality hypothesis 3.
The random speed and run period variable pair, is conditional upon and can be drawn from a conditional PDF, denoted by of the form
| [S26] |
The overall reversal probability, is then formally expressed in terms of and as
| [S27] |
The actual random draw of is not executed in a single step following Eq. S27. Rather, then and then will be drawn in three successive steps, denoted by steps 2.1, 2.2, and 2.3 below, which implement the corresponding sequence of conditionality hypotheses 1, 2, and 3 stated above, as follows.
Given as input are the values of the conditionality variables as stated under step 2 of the random walk algorithm described above, and the observed run database, for
Step 2.1: Draw from Eq. S24.
Find the run index in the run database for which the tuple of observed variables most closely matches the tuple of simulation conditionality variables, in Eq. S24. Then set and use it as input to steps 2.2 and 2.3.
The closest match between the foregoing tuples of observed and simulation conditionality variables is determined here by way of a distance cost function defined by
| [S28] |
where the variable ranges and are defined in Eqs. S22 and S23. The closest match is then defined as the run index that minimizes In the (very unlikely) event of a tie, with multiple values, say, giving the same minimal value of the tie is broken by drawing the value randomly with uniform probability from the set
Step 2.2: Draw θi from Eq. S25.
Find the run index in the run database for which and the tuple of continuous observed variables most closely matches the tuple of continuous conditionality variables, in Eq. S25. Then set
Analogous to step 2.1, the closest match is defined here as the run index that minimizes the metric
| [S29] |
subject to the constraint that and with any tie to be broken by a uniformly random draw.
Step 2.3: Draw from Eq. S26.
Find the run index in the run database for which and the tuple of continuous observed variables, most closely matches the tuple of continuous conditionality variables, in Eq. S26. Then set
Analogous to step 2.2, the closest match is defined here as the run index that minimizes the metric
| [S30] |
subject to the constraint that and with any tie to be broken by a uniformly random draw.
During the early stages of the simulation the observed or simulated density profiles, will likely not exhibit any detectable aggregates, thereby leaving the and variables in Eqs. S24–S30 undefined. In those cases, we do not enforce the corresponding conditionalities by formally letting the normalization factors and go to infinity in Eqs. S28–S30, which is equivalent to simply dropping the and terms from the respective expressions on the right-hand sides of these equations.
It is imperative here to normalize the absolute difference term of each contributing variable in Eqs. S28–S30, by dividing by the respective variable range from Eqs. S22 and S23. For example, in Eq. S30 the four contributing conditionality variables and are each measured in a different physical unit, and hence they must be nondimensionalized before they can be added in any meaningful way. Using the variable ranges from Eqs. S22 and S23 as the normalizing divisor has the effect of treating the distance contributions from all four variables on an equal footing. If falls within the biophysically “reasonable” range, defined by the range of the observed values, then the dimensionless term in Eq. S30 falls within the interval [0 1]. The same is true for if falls within the range of the observed values, and likewise for the terms and As a consequence, each of the four terms in Eq. S30 carries a priori equal weight in contributing to the cost function
Acknowledgments
The research reported here was supported by the National Science Foundation under Awards MCB-1411891 (to L.J.S.) and MCB-1411780 (to O.A.I.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1620981114/-/DCSupplemental.
References
- 1.Yang Z, Higgs PI, editors. Myxobacteria. Caister Academic; Norfolk, UK: 2014. [Google Scholar]
- 2.Bretschneider T, Othmer HG, Weijer CJ. Progress and perspectives in signal transduction, actin dynamics, and movement at the cell and tissue level: Lessons from Dictyostelium. Interface Focus. 2016;6:20160047. doi: 10.1098/rsfs.2016.0047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aman A, Piotrowski T. Cell migration during morphogenesis. Dev Biol. 2010;341:20–33. doi: 10.1016/j.ydbio.2009.11.014. [DOI] [PubMed] [Google Scholar]
- 4.Solnica-Krezel L, Sepich DS. Gastrulation: Making and shaping germ layers. Annu Rev Cell Dev Biol. 2012;28:687–717. doi: 10.1146/annurev-cellbio-092910-154043. [DOI] [PubMed] [Google Scholar]
- 5.Theveneau E, Mayor R. Neural crest delamination and migration: From epithelium-to-mesenchyme transition to collective cell migration. Dev Biol. 2012;366:34–54. doi: 10.1016/j.ydbio.2011.12.041. [DOI] [PubMed] [Google Scholar]
- 6.Friedl P, Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat Rev Mol Cell Biol. 2009;10:445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 7.Park S, Greco V, Cockburn K. Live imaging of stem cells: Answering old questions and raising new ones. Curr Opin Cell Biol. 2016;43:30–37. doi: 10.1016/j.ceb.2016.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Delgado I, Torres M. Gradients, waves and timers, an overview of limb patterning models. Semin Cell Dev Biol. 2016;49:109–115. doi: 10.1016/j.semcdb.2015.12.016. [DOI] [PubMed] [Google Scholar]
- 9.Szabó A, Mayor R. Modelling collective cell migration of neural crest. Curr Opin Cell Biol. 2016;42:22–28. doi: 10.1016/j.ceb.2016.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Iber D, Zeller R. Making sense-data-based simulations of vertebrate limb development. Curr Opin Genet Dev. 2012;22:570–577. doi: 10.1016/j.gde.2012.11.005. [DOI] [PubMed] [Google Scholar]
- 11.Schumacher LJ, Kulesa PM, McLennan R, Baker RE, Maini PK. Multidisciplinary approaches to understanding collective cell migration in developmental biology. Open Biol. 2016;6:160056. doi: 10.1098/rsob.160056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Masuzzo P, Van Troys M, Ampe C, Martens L. Taking aim at moving targets in computational cell migration. Trends Cell Biol. 2016;26:88–110. doi: 10.1016/j.tcb.2015.09.003. [DOI] [PubMed] [Google Scholar]
- 13.Kuspa A, Plamann L, Kaiser D. Identification of heat-stable A-factor from Myxococcus xanthus. J Bacteriol. 1992;174:3319–3326. doi: 10.1128/jb.174.10.3319-3326.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pathak DT, et al. Cell contact-dependent outer membrane exchange in myxobacteria: Genetic determinants and mechanism. PLoS Genet. 2012;8:e1002626. doi: 10.1371/journal.pgen.1002626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mauriello EMF, Mignot T, Yang Z, Zusman DR. Gliding motility revisited: How do the myxobacteria move without flagella? Microbiol Mol Biol Rev. 2010;74:229–249. doi: 10.1128/MMBR.00043-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Balagam R, Igoshin OA. Mechanism for collective cell alignment in Myxococcus xanthus bacteria. PLoS Comput Biol. 2015;11:e1004474. doi: 10.1371/journal.pcbi.1004474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lux R, Li Y, Lu A, Shi W. Detailed three-dimensional analysis of structural features of Myxococcus xanthus fruiting bodies using confocal laser scanning microscopy. Biofilms. 2004;1:293–303. [Google Scholar]
- 18.Berleman JE, et al. Exopolysaccharide microchannels direct bacterial motility and organize multicellular behavior. ISME J. 2016;10:2620–2632. doi: 10.1038/ismej.2016.60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xie C, Zhang H, Shimkets LJ, Igoshin OA. Statistical image analysis reveals features affecting fates of Myxococcus xanthus developmental aggregates. Proc Natl Acad Sci USA. 2011;108:5915–5920. doi: 10.1073/pnas.1018383108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Curtis PD, Taylor RG, Welch RD, Shimkets LJ. Spatial organization of Myxococcus xanthus during fruiting body formation. J Bacteriol. 2007;189:9126–9130. doi: 10.1128/JB.01008-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang H, et al. Quantifying aggregation dynamics during Myxococcus xanthus development. J Bacteriol. 2011;193:5164–5170. doi: 10.1128/JB.05188-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jelsbak L, Søgaard-Andersen L. Pattern formation by a cell surface-associated morphogen in Myxococcus xanthus. Proc Natl Acad Sci USA. 2002;99:2032–2037. doi: 10.1073/pnas.042535699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thutupalli S, Sun M, Bunyak F, Palaniappan K, Shaevitz JW. Directional reversals enable Myxococcus xanthus cells to produce collective one-dimensional streams during fruiting-body formation. J R Soc Interface. 2015;12:20150049. doi: 10.1098/rsif.2015.0049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sliusarenko O, Zusman DR, Oster G. Aggregation during fruiting body formation in Myxococcus xanthus is driven by reducing cell movement. J Bacteriol. 2007;189:611–619. doi: 10.1128/JB.01206-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kearns DB, Shimkets LJ. Chemotaxis in a gliding bacterium. Proc Natl Acad Sci USA. 1998;95:11957–11962. doi: 10.1073/pnas.95.20.11957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhou T, Nan B. Exopolysaccharides promote Myxococcus xanthus social motility by inhibiting cellular reversals. Mol Microbiol. 2017;103:729–743. doi: 10.1111/mmi.13585. [DOI] [PubMed] [Google Scholar]
- 27.Kearns DB, et al. Identification of a developmental chemoattractant in Myxococcus xanthus through metabolic engineering. Proc Natl Acad Sci USA. 2001;98:13990–13994. doi: 10.1073/pnas.251484598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bode HB, et al. Straight-chain fatty acids are dispensable in the myxobacterium Myxococcus xanthus for vegetative growth and fruiting body formation. J Bacteriol. 2006;188:5632–5634. doi: 10.1128/JB.00438-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kim SK, Kaiser D. Cell alignment required in differentiation of Myxococcus xanthus. Science. 1990;249:926–928. doi: 10.1126/science.2118274. [DOI] [PubMed] [Google Scholar]
- 30.Shi W, Ngok FK, Zusman DR. Cell density regulates cellular reversal frequency in Myxococcus xanthus. Proc Natl Acad Sci USA. 1996;93:4142–4146. doi: 10.1073/pnas.93.9.4142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Igoshin OA, Welch R, Kaiser D, Oster G. Waves and aggregation patterns in myxobacteria. Proc Natl Acad Sci USA. 2004;101:4256–4261. doi: 10.1073/pnas.0400704101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sozinova O, Jiang Y, Kaiser D, Alber M. A three-dimensional model of myxobacterial aggregation by contact-mediated interactions. Proc Natl Acad Sci USA. 2005;102:11308–11312. doi: 10.1073/pnas.0504259102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sozinova O, Jiang Y, Kaiser D, Alber M. A three-dimensional model of myxobacterial fruiting-body formation. Proc Natl Acad Sci USA. 2006;103:17255–17259. doi: 10.1073/pnas.0605555103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Holmes AB, Kalvala S, Whitworth DE. Spatial simulations of myxobacterial development. PLoS Comput Biol. 2010;6:e1000686. doi: 10.1371/journal.pcbi.1000686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Starruß J, Bley T, Søgaard-Andersen L, Deutsch A. A new mechanism for collective migration in Myxococcus xanthus. J Stat Phys. 2007;128:269–286. [Google Scholar]
- 36.Hendrata M, Yang Z, Lux R, Shi W. Experimentally guided computational model discovers important elements for social behavior in myxobacteria. PLoS One. 2011;6:e22169. doi: 10.1371/journal.pone.0022169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sliusarenko O, Neu J, Zusman DR, Oster G. Accordion waves in Myxococcus xanthus. Proc Natl Acad Sci USA. 2006;103:1534–1539. doi: 10.1073/pnas.0507720103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gejji R, Lushnikov PM, Alber M. Macroscopic model of self-propelled bacteria swarming with regular reversals. Phys Rev E Stat Nonlin Soft Matter Phys. 2012;85:021903. doi: 10.1103/PhysRevE.85.021903. [DOI] [PubMed] [Google Scholar]
- 39.Lander AD. How cells know where they are. Science. 2013;339:923–927. doi: 10.1126/science.1224186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Morelli LG, Uriu K, Ares S, Oates AC. Computational approaches to developmental patterning. Science. 2012;336:187–191. doi: 10.1126/science.1215478. [DOI] [PubMed] [Google Scholar]
- 41.Sager B, Kaiser D. Two cell-density domains within the Myxococcus xanthus fruiting body. Proc Natl Acad Sci USA. 1993;90:3690–3694. doi: 10.1073/pnas.90.8.3690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Botev ZI, Grotowski JF, Kroese DP. Kernel density estimation via diffusion. Ann Stat. 2010;38:2916–2957. [Google Scholar]
- 43.Clark AG, Vignjevic DM. Modes of cancer cell invasion and the role of the microenvironment. Curr Opin Cell Biol. 2015;36:13–22. doi: 10.1016/j.ceb.2015.06.004. [DOI] [PubMed] [Google Scholar]
- 44.Ellenbroek SIJ, van Rheenen J. Imaging hallmarks of cancer in living mice. Nat Rev Cancer. 2014;14:406–418. doi: 10.1038/nrc3742. [DOI] [PubMed] [Google Scholar]
- 45.Lock JG, et al. Plasticity in the macromolecular-scale causal networks of cell migration. PLoS One. 2014;9:e90593. doi: 10.1371/journal.pone.0090593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bastos AM, Schoffelen J-M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front Syst Neurosci. 2016;9:175. doi: 10.3389/fnsys.2015.00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Moine A, et al. Functional organization of a multimodular bacterial chemosensory apparatus. PLoS Genet. 2014;10:e1004164. doi: 10.1371/journal.pgen.1004164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Xu Q, Black WP, Cadieux CL, Yang Z. Independence and interdependence of Dif and Frz chemosensory pathways in Myxococcus xanthus chemotaxis. Mol Microbiol. 2008;69:714–723. doi: 10.1111/j.1365-2958.2008.06322.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Curtis PD, Geyer R, White DC, Shimkets LJ. Novel lipids in Myxococcus xanthus and their role in chemotaxis. Environ Microbiol. 2006;8:1935–1949. doi: 10.1111/j.1462-2920.2006.01073.x. [DOI] [PubMed] [Google Scholar]
- 50.Iniesta AA, García-Heras F, Abellón-Ruiz J, Gallego-García A, Elías-Arnanz M. Two systems for conditional gene expression in Myxococcus xanthus inducible by isopropyl-β-D-thiogalactopyranoside or vanillate. J Bacteriol. 2012;194:5875–5885. doi: 10.1128/JB.01110-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kashefi K, Hartzell PL. Genetic suppression and phenotypic masking of a Myxococcus xanthus frzF- defect. Mol Microbiol. 1995;15:483–494. doi: 10.1111/j.1365-2958.1995.tb02262.x. [DOI] [PubMed] [Google Scholar]
- 52.Edelstein AD, et al. Advanced methods of microscope control using µManager software. Protocol. 2014;1:1–10. doi: 10.14440/jbm.2014.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jaqaman K, et al. Robust single-particle tracking in live-cell time-lapse sequences. Nat Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jonker R, Volgenant A. A shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing. 1987;38:325–340. [Google Scholar]
- 55.Davison AC, Hinkley DV. Bootstrap Methods and Their Application. Cambridge Univ Press; New York: 1997. [Google Scholar]
- 56.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. 2nd Ed Springer; New York: 2009. [Google Scholar]
- 57.Chen H, Keseler IM, Shimkets LJ. Genome size of Myxococcus xanthus determined by pulsed-field gel electrophoresis. J Bacteriol. 1990;172:4206–4213. doi: 10.1128/jb.172.8.4206-4213.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Challa S, Morelande MR, Musicki D, Evans RJ. Fundamentals of Object Tracking. Cambridge Univ Press; New York: 2011. [Google Scholar]
- 59.Crocker J, Grier D. Methods of digital video microscopy for colloidal studies. J Colloid Interface Sci. 1996;310:298–310. [Google Scholar]
- 60.Freedman D, Diaconis P. On the histogram as a density estimator: L 2 theory. Probab Theory Relat Fields. 1981;57:453–476. [Google Scholar]