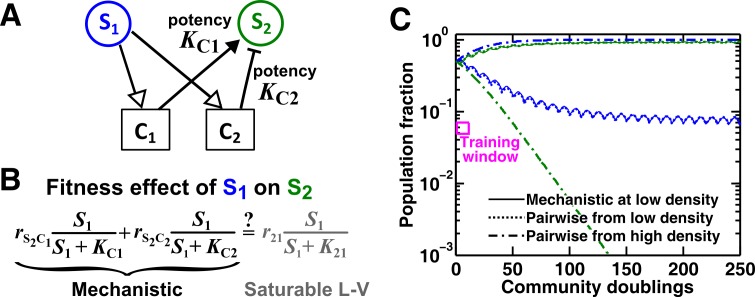
Figure 5. An example of a two-mediator interaction where a saturable L-V pairwise model may succeed or fail depending on initial conditions.

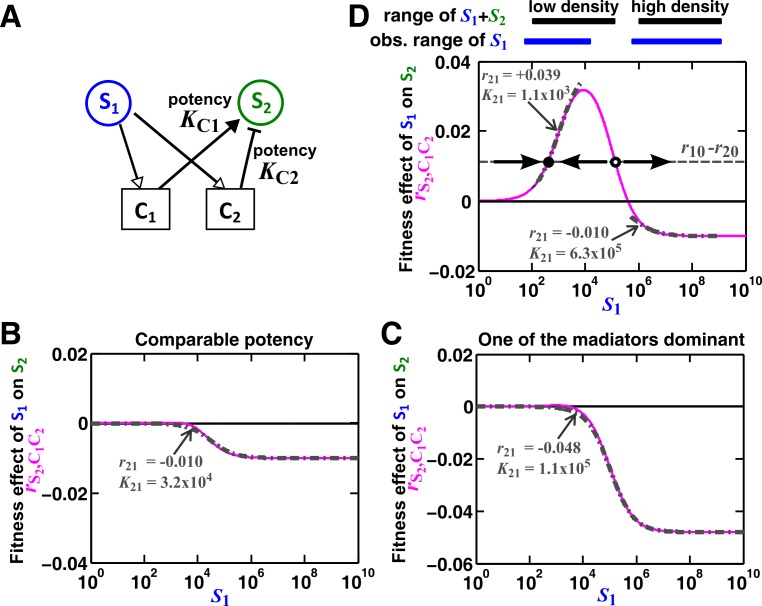
(A) One species can affect another species via two reusable mediators, each with a different potency ${\displaystyle K_{Ci}}$ where ${\displaystyle K_{Ci}}$ is $K_{S_2{C}_i}{r}_{10}/{\beta }_{C_i{S}_1}$ (Methods-Conditions under which a saturable L-V pairwise model can represent one species influencing another via two reusable mediators). A low ${\displaystyle K_{Ci}}$ indicates a strong potency (e.g. high release of C_i by S₁ or low ${\displaystyle C_i}$ required to achieve half-maximal influence on S₂). (B) Under what conditions can an interaction via two reusable mediators with saturable effects on recipients be approximated by a saturable L-V pairwise model? (C) A community where the success or failure of a saturable L-V pairwise model depends on initial conditions. Here, ${\displaystyle K_{C1}}$= 10³ cells/ml and ${\displaystyle K_{C2}}$= 10⁵ cells/ml. Community dynamics starting at low ${\displaystyle S_1}$ (solid) can be predicted if the saturable L-V pairwise model is derived from reference dynamics starting at low (dotted). However, if we use a saturable L-V pairwise model derived from a community with high initial ${\displaystyle S_1}$, prediction is qualitatively wrong (dash dot line). See Figure 5—figure supplement 1D for an explanation why a saturable L-V pairwise model estimated at one community density may not be applicable to another community density. Simulation parameters are listed in Figure 5—source data 1 .

DOI: http://dx.doi.org/10.7554/eLife.25051.020

Figure 5—figure supplement 1. Except under special conditions, a pairwise interaction through two mediators may not be represented by a single saturable L-V model.

(A) Consider the interaction in Figure 5. The fitness effect of S₁ on S₂ via C₁ and C₂ is $r_{S_2,C_1{C}_2}=\frac{r_{S_2{C}_1}{S}_1}{S_1+K_{S_2{C}_1}{r}_{10}/{\beta }_{C_1{S}_1}}+\frac{r_{S_2{C}_2}{S}_1}{S_1+K_{S_2{C}_2}{r}_{10}/{\beta }_{C_2{S}_1}}=\frac{r_{S_2{C}_1}{S}_1}{S_1+K_{C_1}}+\frac{r_{S_2{C}_2}{S}_1}{S_1+K_{C_2}}$. (B–C) Under special conditions the fitness effect $r_{S_2,C_1{C}_2}$ (magenta line) can be approximated using a single saturable L-V model (grey dash-dot line) at all densities. These special conditions include when the potencies of two mediators, K_C1 and K_C2, are similar (B) or the potency of one mediator is orders of magnitude stronger than the other (C). Otherwise, saturable L-V pairwise models derived from a low-density community and from a high-density community can have qualitatively different parameters (D). Let’s first consider the low-density case (left black and blue bars corresponding to low total density and therefore low , respectively). When $r_{S_2,C_1{C}_2}$ (magenta line) is above the (${\displaystyle r_{10}-r_{20}}$) line (grey dashed line), the fitness of S₂ ($r_{S_2,C_1{C}_2}+r_{20}$) will be higher than the fitness of S₁. Thus, even though S₁ grows at its basal fitness during a dilution cycle, S₁ fraction will decrease. Thus ${\displaystyle S_1}$ will decrease at the next dilution cycle when total density is reset to a pre-fixed level (arrow pointing towards lower ${\displaystyle S_1}$). In contrast, when $r_{S_2,C_1{C}_2}<r_{10}-r_{20}$, S₁ population fraction and ${\displaystyle S_1}$ will increase at the next dilution cycle (arrow pointing towards higher ${\displaystyle S_1}$). Thus, the dynamics will converge to a steady state ratio (filled dot). Interaction coefficient of a saturable L-V (grey dash-dot line) is estimated to be a positive value ( =+0.039). In contrast, in the high-density case (right black and blue bars), $r_{10}>r_{S_2,C_1{C}_2}+r_{20}$, and S₂ goes extinct. Interaction coefficient of a saturable L-V (grey dash-dot line) is estimated to be a negative value ( = −0.010). As a result, a saturable L-V pairwise model with parameters estimated at high densities cannot predict communities at low densities (Figure 5). All parameters are listed in Figure 5—source data 2.

DOI: http://dx.doi.org/10.7554/eLife.25051.023