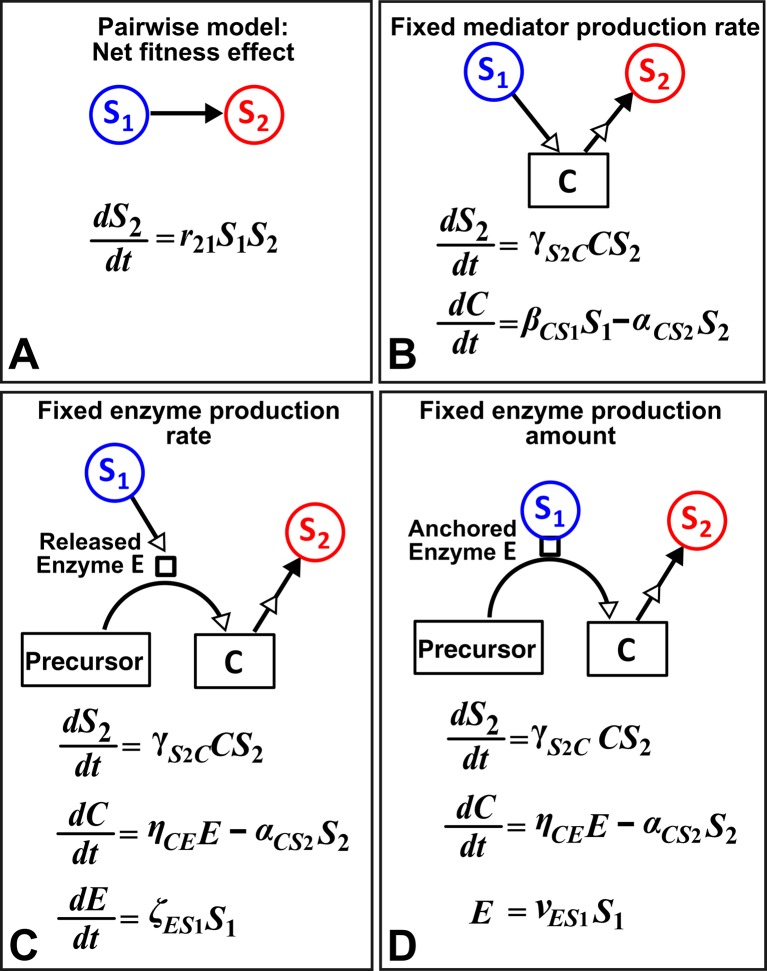
Figure 8. Different levels of abstraction in a mechanistic model.
How one species (S1) may influence another (S2) can be mechanistically modeled at different levels of abstraction. For simplicity, here we assume that interaction strength scales in a linear (instead of saturable) fashion with respect to mediator concentration or species density. The basal fitness of S2 is zero. (A) In the simplest form, S1 stimulates S2 in an L-V pairwise model. (B) In a mechanistic model, we may realize that S1 stimulates S2 via a mediator C which is consumed by S2. The corresponding mechanistic model is given. (C) Upon probing more deeply, it may become clear that S1 stimulates S2 via an enzyme E, where E degrades an abundant precursor (such as cellulose) to generate mediator C (such as glucose). In the corresponding mechanistic model, we may assume that E is released by S1 at a rate and that E liberates C at a rate . (D) If instead E is anchored on the cell surface (e.g. cellulosome), then E is proportional to S1. If we substitute E into the second equation, then (B) and (D) become equivalent. Thus, when enzyme is anchored on cell surface but not when enzyme is released, the mechanistic knowledge of enzyme can be neglected.