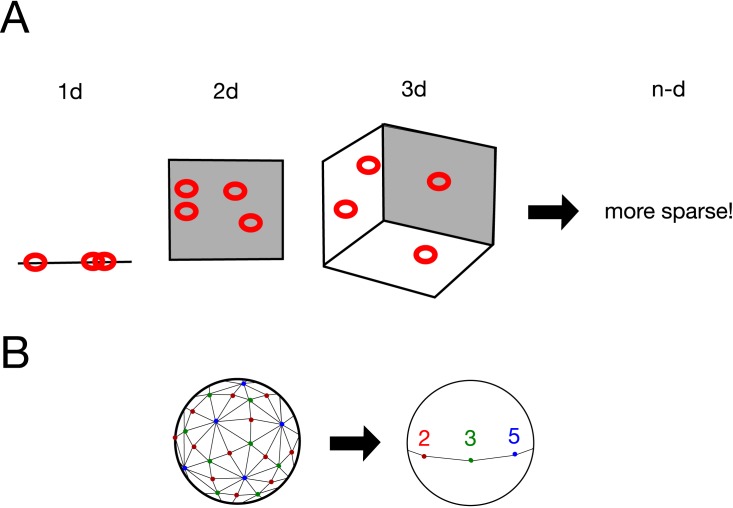
Fig 2. “Curse of dimensionality” and a possible solution.

(A) “Curse of dimensionality” effects when there is a sparse geometric distribution of data points; see also Ronan et al. (2016). (B) Example of geometric conversion to a simpler system: quotient of icosahedral tessellation by I on a Riemann sphere. 2 (red points), 3 (green points), and 5 (blue points) correspond to the midpoints of the edges, the barycenters of the faces, and the vertices, respectively; see also Cornelissen and Kato (2005).