Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2017 Jun 14;7:3511. doi: 10.1038/s41598-017-03412-6

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2017

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

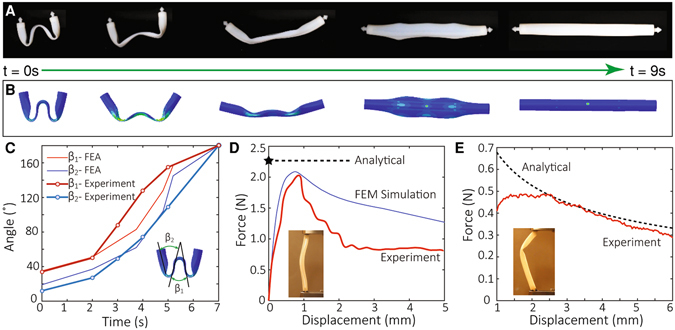
Properties of the slitted tubular struts via 3D printing. (A) The snapshot images of the free recovery sequence of a strut at 65 °C. (B) The predictions from the corresponding finite element method (FEM) simulation. (C) The opening angles of the strut during the free recovery and the comparison with the FEM simulation. The inset shows the definitions of the two opening angles. (D) The critical load of a single strut during uniaxial compression from the experiment and the FEM simulation. The inset shows the experimental setup. Considering the boundary condition in the experimental setup, a 0.75 effective length ratio gives the upper bound on the critical buckling load of a single strut. In practical designs, because the joints in our tensegrity are almost free in rotation, 1.0 effective length shall be used. (E) The critical load of a single strut during its recovery. Derivation for the analytical prediction is elaborated in SI. In the experiment, a small initial displacement (1 mm) is imposed to prevent the opened cross section from closing.