Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jul 1.
Published in final edited form as: J Mech Behav Biomed Mater. 2017 Feb 20;71:192–200. doi: 10.1016/j.jmbbm.2017.02.020

MODELING THE INFLUENCE OF ACUTE CHANGES IN BLADDER ELASTICITY ON PRESSURE AND WALL TENSION DURING FILLING

Firdaweke G Habteyes a, S Omid Komari a, Anna S Nagle a, Adam P Klausner b, Rebecca L Heise c, Paul H Ratz d, John E Speich a,*
PMCID: PMC5472102  NIHMSID: NIHMS862797  PMID: 28343086

Abstract

Tension-sensitive nerves in the bladder wall are responsible for providing bladder sensation. Bladder wall tension, and therefore nerve output, is a function of bladder pressure, volume, geometry and material properties. The elastic modulus of the bladder is acutely adjustable, and this material property is responsible for adjustable preload tension exhibited in human and rabbit detrusor muscle strips and dynamic elasticity revealed during comparative-fill urodynamics in humans. A finite deformation model of the bladder was previously used to predict filling pressure and wall tension using uniaxial tension test data and the results showed that wall tension can increase significantly during filling with relatively little pressure change. In the present study, published uniaxial rabbit detrusor data were used to quantify regulated changes in the elastic modulus, and the finite deformation model was expanded to illustrate the potential effects of elasticity changes on pressure and wall tension during filling. The model demonstrates a shift between relatively flat pressure-volume filling curves, which is consistent with a recent human urodynamics study, and also predicts that dynamic elasticity would produce significant changes in wall tension during filling. The model results support the conclusion that acute regulation of bladder elasticity could contribute to significant changes in wall tension for a given volume that could lead to urgency, and that a single urodynamic fill may be insufficient to characterize bladder biomechanics. The model illustrates the potential value of quantifying wall tension in addition to pressure during urodynamics.

Keywords: Urodynamics, detrusor smooth muscle, length-tension curve, pressure-volume curve, adjustable preload tension, dynamic elasticity

1. Introduction

1.1. Significance of bladder wall tension during filling

Tension-sensitive nerves in the bladder wall provide fullness information that is interpreted as bladder sensation and urgency during filling (Kanai and Andersson 2010). Bladder wall tension at a given volume is a function of the vesical pressure, geometry and material properties. Clinical urodynamics studies are used to quantify the pressure-volume relationship throughout filling and the overall bladder compliance (Δvolume/Δpressure) for a particular fill (Mahfouz, Al Afraa et al. 2012); however, these studies often reveal only small increases in filling phase pressures in patients with or without heightened urgency (Frenkl, Railkar et al. 2011). These standard pressure measurements do not necessarily reflect the underlying wall tension, which may correlate more closely with urgency.

1.2. Bladder elasticity is acutely regulated

Several studies have demonstrated that repeated stretches of “passive” rabbit, mouse or human bladder strips (Speich, Borgsmiller et al. 2005, Speich, Quintero et al. 2006, Ratz and Speich 2010, Rubod, Brieu et al. 2012, Colhoun, Speich et al. 2015) can cause strain-induced stress softening and reveal the Mullins effect (Mullins, Tobin et al. 1966). Likewise, repeated filling of isolated mouse bladders (Speich, Southern et al. 2012) can soften the bladder, just as repeated stretches of a latex balloon make it easier to inflate. Moreover, strain-induced stress softening can be reversed by active contraction at short muscle lengths (Speich, Borgsmiller et al. 2005, Almasri, Ratz et al. 2010, Colhoun, Speich et al. 2015). Thus, bladder wall elasticity is strain-history-dependent and activation-history-dependent. In addition, adjustable preload tension in mouse bladder is elevated following partial bladder outlet obstruction (Speich, Southern et al. 2012). Most importantly, strain-induced stress softening has been identified in human detrusor (Colhoun, Speich et al. 2015) and quantified as dynamic elasticity due to strain-induced stress softening during a pilot human comparative-fill urodynamics study (Colhoun, Klausner et al. 2016). Furthermore, the change in elasticity associated with repeated passive filling has been shown to be greater in a partial bladder outlet obstructed mouse model of detrusor overactivity (Speich, Southern et al. 2012). Together, these preclinical and clinical data provide evidence that detrusor overactivity, and potentially overactive bladder in humans, may be associated with dynamic elasticity.

1.3. Study objectives

The overall objectives of the present study were to use mathematical modeling to demonstrate that wall tension and stress (tension/cross-sectional area) may increase significantly during filling with relatively uniform vesical pressures and predict the extent to which acute changes in bladder elasticity may affect wall stress during filling. The specific objectives were to 1) use published uniaxial length-tension data (Speich, Dosier et al. 2007) to determine ranges for regulated changes in detrusor elasticity in rabbit bladder and 2) use hyperelastic models of bladder filling (Watanabe, Akiyama et al. 1981, Ogden 1984) to predict the potential effects of elasticity changes on bladder pressure and wall stress during filling.

2. Theory and Methods

2.1. Watanabe’s continuum model of bladder elasticity

Hyperelastic continuum models have been developed to analyze the complex behavior of highly deformable materials (Holzapfel 2000). Watanabe et al. (Watanabe, Akiyama et al. 1981) used finite deformation theory to develop a hyperelastic continuum model for the bladder, which was assumed to be spherical and made of an isotropic incompressible material (Janz, Kubert et al. 1980, Watanabe, Akiyama et al. 1981, Saito and Oki 1982). For uniaxial extension, the relationship between uniaxial stress, σ1, and the uniaxial extension ratio (strain), λ1, was given by the equation:

σ1=aλ1(λ1-1)(b-1)+aλ1(1-1λ1)(b-1) 1

Watanabe determined material property parameters a and b by fitting this equation to data from a uniaxial length-tension experiment performed on strips of canine bladder (Watanabe, Akiyama et al. 1981). Parameters a and b regulate the magnitude and curvature, respectively, of the stress-strain curve. For spherical bladder filling, the relationship between wall stress, σ, the extension ratio of the bladder radius, λ, and the material property parameters, a and b, was given by the equation:

σ=aλ(λ-1)(b-1)+aλ2(1-1λ2)(b-1) 2

In addition, bladder filling pressure, P, was defined as a function of σ; bladder mass, m; bladder density, ρ; and volume, V; using the equation:

P=2mσ3ρV 3

This model produced a relatively flat pressure-volume curve, as typically observed in a clinical cystometery (Mahfouz, Al Afraa et al. 2012, Colhoun, Klausner et al. 2016), and a wall stress curve that continued to rise with increasing volume (Watanabe, Akiyama et al. 1981).

2.2. Ogden’s continuum model applied to bladder elasticity

Boubaker et al. (Boubaker, Haboussi et al. 2015) applied a hyperelastic material deformation model developed by Ogden (Ogden 1984) to the bladder using the following equation for the relationship between uniaxial stress, σ1, and strain, λ1:

σ1=a(λ1(b-1)-λ1(-b2)-1) 4

This model was fit to experimental data from longitudinal and transverse strips from a pig bladder find material parameters a and b. Then, a finite element model and geometric parameters from a CT scan of a human cadaver to predict bladder filling pressure. The results showed only a small increase in pressure throughout the normal filling range for a human bladder, consistent with clinical cystometry (Frenkl, Railkar et al. 2011, Mahfouz, Al Afraa et al. 2012).

2.3. Application of the Watanabe and Ogden models to predict the effect of strain-induced stress softening on bladder pressure and wall stress

For the present study, the Watanabe and Ogden models were used to predict the effect of acutely regulated detrusor elasticity on filling pressures and wall stresses. First, uniaxial length-tension data from a previous study revealing changes in detrusor elasticity in rabbit detrusor strips (Speich, Dosier et al. 2007) was converted to length-stress data (Fig. 1A) using an estimated undeformed cross-sectional area of 0.9 mm2 (Speich, Dosier et al. 2007). These data show a region in which elasticity could be adjusted between a loading curve consisting of pseudo-steady-state stress values at a series of increasing length (strain) increments (Fig. 1A, loading) and an unloading curve consisting of stress values at a series of decreasing length increments (Fig. 1A, unloading). Next, the first seven stress data points of the loading curve were fit to a line, and this line was extrapolated to estimate the muscle strip length corresponding to zero stress where the strain ratio was defined to be unity (Fig. 1B). Then, Equation 1 was fit separately to the stress-strain data for the loading and unloading curves in Fig 2A to determine the material property parameters a and b for the Watanabe model for each curve. Similarly, Equation 4 from was fit separately the loading and unloading data in Fig 2A to determine material property parameters a and b for the Ogden model.

Fig 1.

Fig 1

Open in a new tab

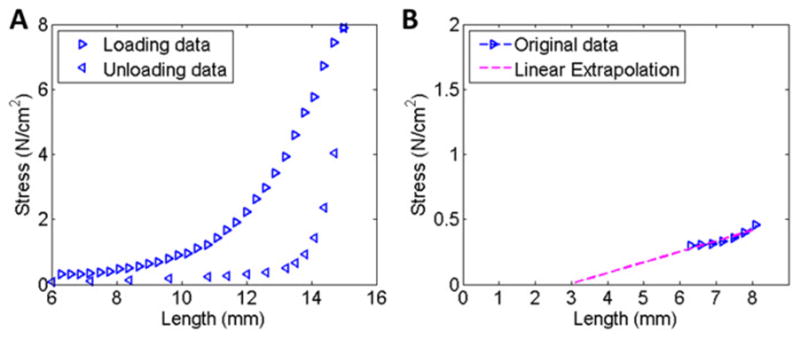
A Length-stress data for a loading-unloading protocol for rabbit detrusor smooth muscle. B Linear fit to the first seven data points from the loading curve in panel A, identifying the zero-stress length as 3mm.

Fig 2.

Fig 2

Open in a new tab

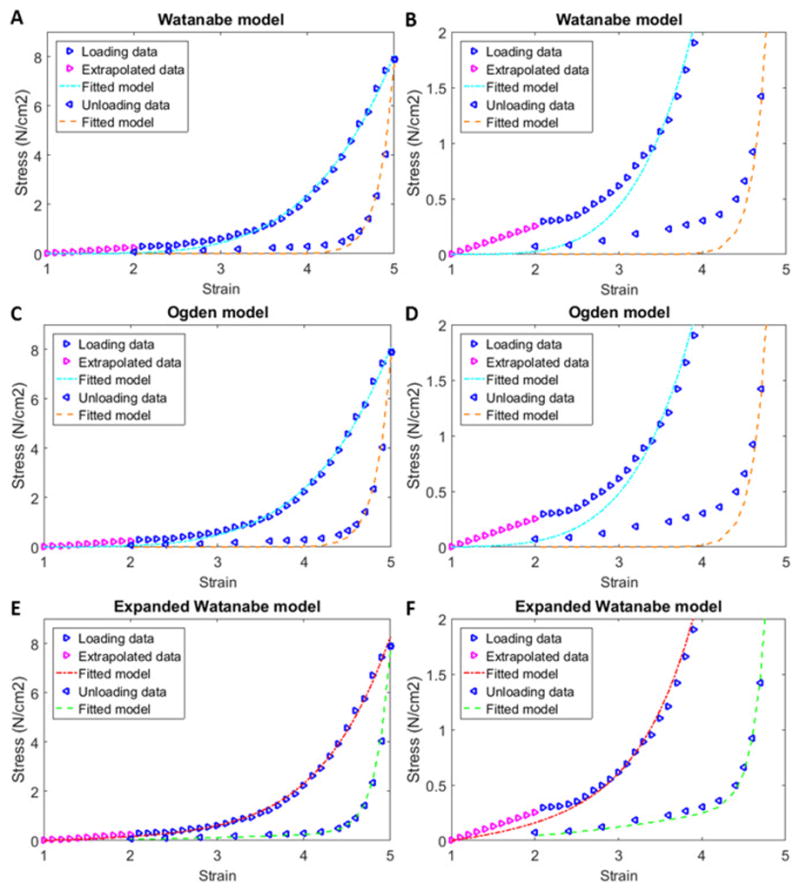
Stress-strain curves for the loading and unloading data from Figs 1A–B, with fits to Watanabe’s model (Watanabe, Akiyama et al. 1981) (A), Ogden’s model (Ogden 1984) (C) and an expanded Watanabe model (E). Panels B, D and F are zoomed regions of panels A, C, and E, respectively, which show the quality of the fits at smaller stress values.

The relationship between the initial muscle strip length, Ls, and the initial outer radius, ro, was determined using the circumference relationship

Ls=f(2πro) 5

where f is the fraction of the circumference corresponding to the muscle strip length. The volume of bladder tissue, Vtissue, was used to relate the inner radius, ri, to the outer radius using the equation

Vtissue=mρ=4π3(ro3-ri3) 6

Bladder density and mass were estimated to be 1.05 g/cm3 and 2.5 g, respectively, based on previous studies (Levin, Longhurst et al. 1990, Murphy 2011). The initial inner radius to the initial bladder volume, Vinitial, was related the inner radius using the sphere volume equation

Vinitial=4π3ri3 7

Equations 5–7 were combined to identify the relationship between the initial strip length and the initial volume

Vinitial=16π(Lsf)3-mρ 8

Finally, pressure-volume curves (Fig 3A) and wall stress-volume curves (Fig 3B) for the Watanabe model were produced for the loading and unloading curves in Fig 2A using Equations 3 and 2, respectively. Similarly, pressure-volume (Fig 3C) and wall stress-volume (Fig 3D) curves were produced for Ogden model using Equations 3 and 4, respectively

Fig 3.

Fig 3

Open in a new tab

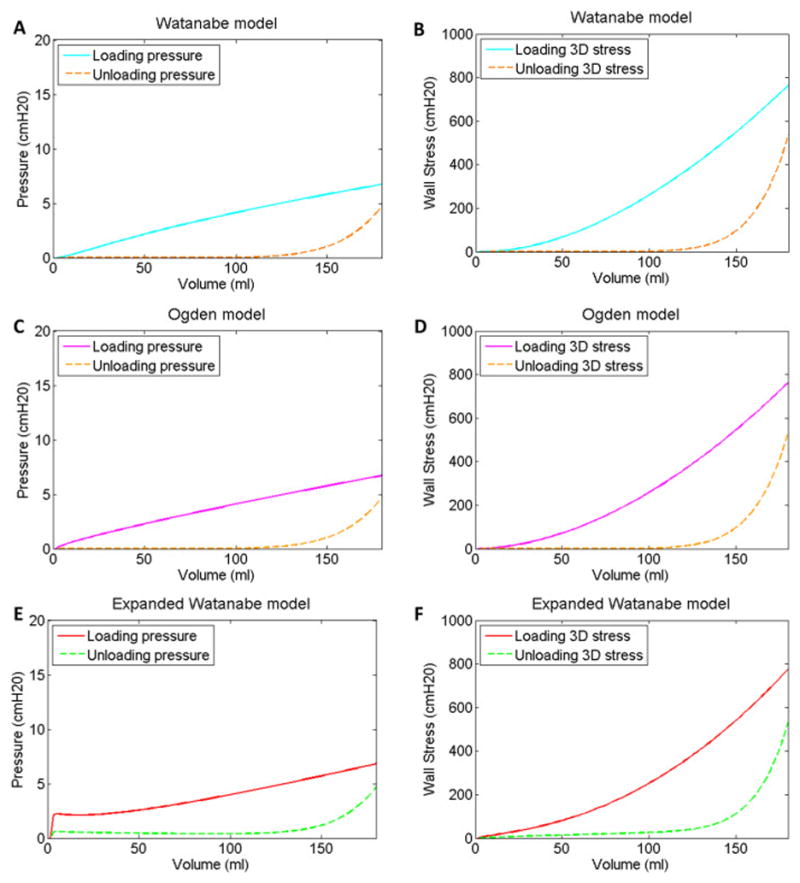
Pressure-volume (A, C & E) and wall stress-volume (B, D & F) curves corresponding to the Watanabe model fits (A & B), Ogden (C & D) and expanded Watanabe model fits (E & F) to the loading and unloading curves in Fig 2A based on an initial bladder volume of 1.5 ml.

2.4. An expanded Watanabe continuum model of bladder elasticity

To potentially obtain a better fit to the experimental data, Watanabe’s model (Watanabe, Akiyama et al. 1981) was expanded to include two additional terms that were identical to the original two terms except for new material property parameters c and d. For this “expanded Watanabe model,” the uniaxial extension, the stress-strain relationship was given by the equation:

σ1=aλ1(λ1-1)(b-1)+aλ1(1-1λ1)(b-1)+cλ1(λ1-1)(d-1)+cλ1(1-1λ1)(d-1) 9

For spherical bladder filling, the wall stress-strain relationship for the expanded Watanabe model was given by the equation:

σ=aλ(λ-1)(b-1)+aλ2(1-1λ2)(b-1)+cλ(λ-1)(d-1)+cλ2(1-1λ2)(d-1) 10

Equation 9 was fit separately to the uniaxial loading and unloading stress-strain curves in Fig 2E and 2F to determine the material property parameters a, b, c and d for the expanded Watanabe model of bladder elasticity. Finally, pressure-volume curves (Fig 3E) and wall-stress-volume curves (Fig. 3F) were produced for the range of regulated detrusor elasticity using Equations 3 and 10, respectively.

2.5. Curve fitting

Curve fitting was completed using MATLAB software (2011a, MathWorks, Natick, MA). The Nelder-Mead simplex method (fminsearch function) was used to optimize the material property parameters. All material property parameters were constrained to be positive, and parameters b and d for the expanded Watanabe model were constrained to be ≥ 2 in order to keep exponents ≥ 1. The seed values for the material parameters used for each fit are included in Table 1. Percent root-mean-squared (RMS) error values for all material property parameter fits are listed in Table 1.

Table 1.

Material property parameters.

Model Parameter Loading Unloading
Seed Optimized % Error Seed Optimized % Error
Watanabe Model a (cmH2O) 0.1 0.0130 5.91 0.1 1.74x10−13 9.03
b 3 4.48 3 22.51
Ogden Model a (cmH2O) 0.015 0.0011 5.24 0.015 1.9x10−19 8.88
b 6.91 6.53 6.91 29.05
Expanded Watanabe Model a (cmH2O) 0.1 0.0705 3.76 0 1.65x10−14 4.50
b 3 2 20 24.16
c (cmH2O) 0.001 2.21x10−3 0.1 0.0195
d 6 5.64 3 2
Open in a new tab

3. Results

3.1. Determination of length and volume ranges

The first seven uniaxial stress data points in the loading curve in Fig 1A were fit to a line which was extrapolated to predict zero stress at a muscle length of 3mm in Fig 1B. Strain ratios were calculated based on this length to produce the stress-strain data curves in Fig 2.

Equation 7 relates this muscle length to the initial volume. The wall stress-strain relationships in Equations 2 and 9 do not permit an initial volume bladder of zero because this would result in division by zero. The volume corresponding to zero stress was not measured (Speich, Dosier et al. 2007), therefore, a range of three initial volumes (1, 1.5 and 2 ml) was examined. For each initial volume, the pressure-volume curves for the expanded Watanabe model remained relatively flat compared to the increasing wall stress-volume curves (Fig 4E & 4F). The initial bladder circumferences corresponding to these volumes and the fractions of the circumference, f, corresponding to the muscle strip length of 3mm are listed in Table 2. The capacity of an adult rabbit’s bladder was assumed to be 60 ml (Matsumoto, Chichester et al. 2002).

Fig 4.

Fig 4

Open in a new tab

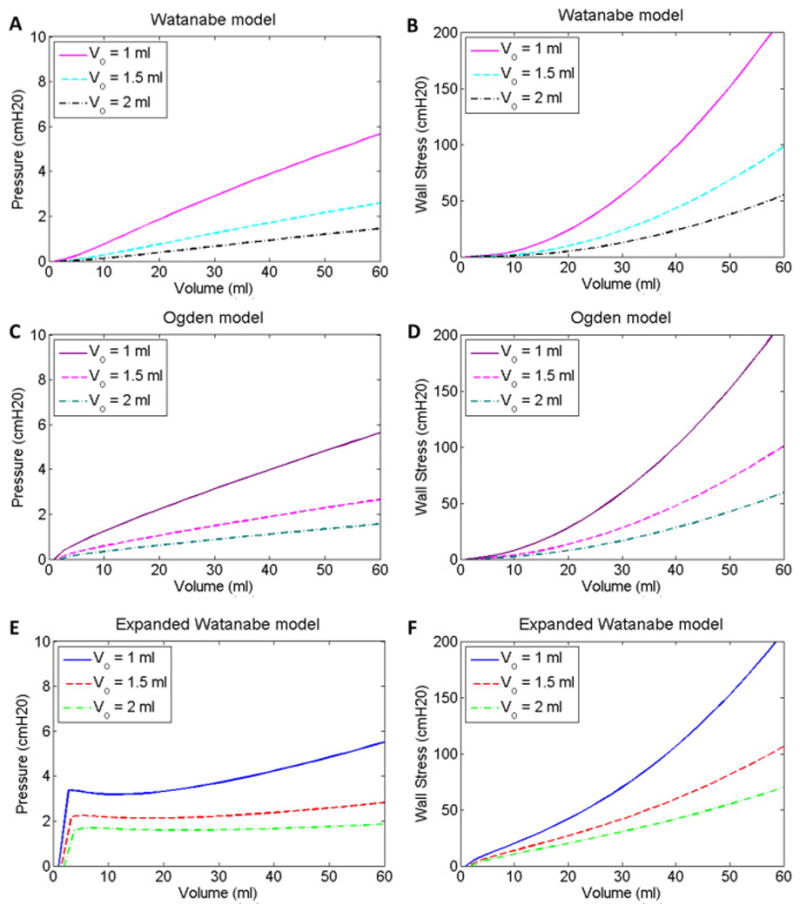
Pressure-volume (A, C & E) and wall stress-volume (B, D & F) curves for initial bladder volumes of 1, 1.5 and 2 ml for the Watanabe model fits (A & B), Ogden (C & D) and expanded Watanabe model fits (E & F) to the loading curve in Fig 2A.

Table 2.

Bladder geometry parameters for a range of initial volumes.

Vinitial (ml) Initial outer circumference (mm) Circumference fraction, f, corresponding to Ls = 3mm Strain ratio, λ, at 60 ml Strain ratio, λ, at 180 ml
0 52.05 1/17.35 2.97 4.25
1 58.5 1/19.5 2.64 3.78
1.5 61.26 1/20.42 2.52 3.61
2 63.75 1/21.25 2.42 3.47
Open in a new tab

3.2. Effect of regulated detrusor compliance on wall stress and pressure

Watanabe’s (Watanabe, Akiyama et al. 1981) uniaxial stress-strain model relationship defined in Equation 1 was fit separately to the loading and unloading curves in Fig 2A, and the corresponding material property parameters a and b are listed in Table 1. These values were used in Equations 2–4 to calculate bladder pressure and wall stress for the Watanabe (Fig 3A & 3B) and Ogden (Fig 3C & 3D) models for a bladder with an initial, unstressed volume of 1.5 ml. The results in Fig 3 are presented for a volume range of 1.5 to 180 ml, which is triple the normal volume range for an adult rabbit (Matsumoto, Chichester, Bratslavsky, Kogan, & Levin, 2002).

Because of the relatively poor fit of the Watanabe and Ogden models (Watanabe, Akiyama et al. 1981, Ogden 1984) at low strain for the curves in Figs 2B and 2D, the previously described expanded Watanabe model was developed by simply placing two of Watanabe’s models in parallel with distinct material property parameters (c and d in addition to a and b). The uniaxial stress-strain relationship for the expanded Watanabe model defined in Equation 9 was fit separately to the loading and unloading curves in Fig 2E, and the corresponding material property parameters a, b, c and d are listed in Table 1. These values were used in Equations 3 and 10 to calculate bladder pressure (Fig 3E) and wall stress (Fig 3F) for a bladder with an initial, unstressed volume of 1.5. The percent errors for the expanded Watanabe model fits were less than those for fits to the Watanabe and Ogden models (Table 1).

4. Discussion

4.1. Adjustable preload tension

As described in the introduction, detrusor smooth muscle strips exhibit adjustable preload tension (Speich, Borgsmiller et al. 2005, Colhoun, Speich et al. 2015). The stress at the first muscle length of the experimental loading curve in Fig 1A (6.3 mm) was not zero because tissues had been previously strain softened and then contracted at 6 mm to reestablish any adjustable preload tension lost to the strain-induced stress softening (Speich, Dosier et al. 2007). This is consistent with another study which showed that preload tension increases even at the muscle length where the restoring contraction(s) are imposed (Almasri, Ratz et al. 2010). In addition, the magnitude of the change in preload tension between the loading and unloading curves in Fig 1A was due to the degree of strain-induced stress softening revealed in this particular experiment, and thus the range of preload tension values shown is likely an underestimate of the potential range of values at each particular muscle length. For example, if the tissues had been stretched to 16 mm instead of 15 mm, the tension value upon unloading to 14 mm would be expected to be reduced due to additional strain-induced stress softening. Most importantly, the present study reveals the dramatic significance that adjustable preload tension could have on bladder pressure and wall stress during filling (Fig 3). Gregersen et al. have shown the Mullins effect in the guinea pig small intestine (Gregersen, Emery et al. 1998) and reversible strain-induced stress softening in the rat esophagus (Jiang, Liao et al. 2014). Thus, adjustable preload tension may have a role in a variety of hollow organs.

4.2. Clinical relevance of the effect of strain-induced stress softening on bladder pressure and wall stress

Standard clinical urodynamic studies measure pressure and infused volume throughout filling; however, the bladder geometric parameters necessary for wall stress calculations are not measured. As a result, variations in bladder geometry are not considered and wall stress is not quantified. Modeling results in Fig 5A show that for the physiological range of 60 ml for an adult rabbit, the pressure curves remained relatively flat throughout filling (Fig 5A). These results are consistent with rabbit urodynamics data (Levin, Monson et al. 1994), especially in the 0–60 ml physiological range. In contrast to the relatively flat pressure curve (Fig 5A), the wall stress curve increased steeply during loading in (Fig 5B). As a result, we anticipate that wall tension measurements would be a better indicator of the load on the mechanosensors responsible for bladder sensation (Kanai and Andersson 2010) and therefore better correlate with increases in bladder sensation during filling. A clinical study is currently underway to incorporate ultrasound with urodynamics to obtain the geometrical measurements necessary to combine with pressure measurements to calculate wall stress and to correlate pressure and wall stress with bladder sensation throughout filling.

Fig 5.

Fig 5

Open in a new tab

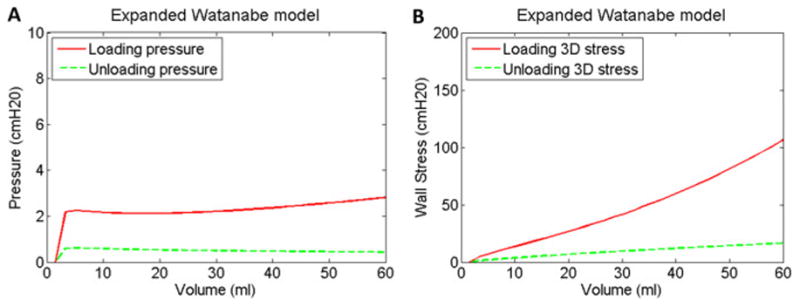
Pressure-volume (A) and wall stress-volume (B) curves for the expanded Watanabe model rescaled from Figs 3B and 3D to show only the assumed physiological range of 60 ml and to emphasize and contrast the relatively flat pressure curves (A) and the steeply increasing wall stress curve during loading (B).

The model results in Fig 5B, demonstrate that adjustable preload tension previously quantified in rabbit bladder strips (Speich, Dosier et al. 2007) can have a dramatic effect on wall stress within the physiological range of rabbit bladder filling. Adjustable preload tension has been identified in human bladder strips (Colhoun, Speich et al. 2015), and the present modeling results indicate that adjustable preload tension could have a significant effect on bladder wall stress during filling. Furthermore, a potential defect in the acute regulation of bladder elasticity could contribute to a significant change in wall stress for a given bladder volume, and therefore alter the load on the mechanosensors responsible for bladder sensation at that volume and contribute to urgency.

The model results in Fig 5A are also consistent with a recent clinical study (Colhoun, Klausner et al. 2016). Fig 6 presents an example of human urodynamic data from an Institutional Review Board-approved comparative-fill urodynamics protocol used to identify dynamic elasticity in the bladder. These data demonstrate dynamic elasticity characterized by 1) decreased filling pressure following a fill-passive emptying (no void) cycle to soften the bladder (Fig 6, shift from red to blue) and 2) increased filling pressure following a fill-active void cycle to reverse the strain-induced stress softening (Fig 6, shift from blue to green). In the previous study, pressure at low volumes following a fill-passive empty cycle was reduced by 54%, and filling pressure following a subsequent fill-active void cycle returned to 84% of the original pressure. Together, these fill-history and active void-history dependent changes in filling pressure demonstrate dynamic elasticity of the bladder wall during filling (Colhoun, Klausner et al. 2016). The present model indicates that a bladder could produce relatively flat pressure curves (Fig 5A) while under two substantially different states of wall stress (Fig 5B). A single urodynamic fill would not necessarily differentiate between the two pressure curves in Fig 5A because relative pressures are measured and the pressure signals are typically zeroed near the onset of filling. Thus, pressure measurements during a single urodynamic fill would not necessarily differentiate the two states of wall stress demonstrated in Fig 5B. Together, the present model results support the conclusion that standard urodynamics in which fill-active void cycles are performed may be insufficient to identify a defect in the regulation of dynamic elasticity. The present model also supports the potential utility of comparative fills with passive and active emptying during urodynamics to more fully elucidate complex bladder biomechanical behavior.

Fig 6.

Fig 6

Open in a new tab

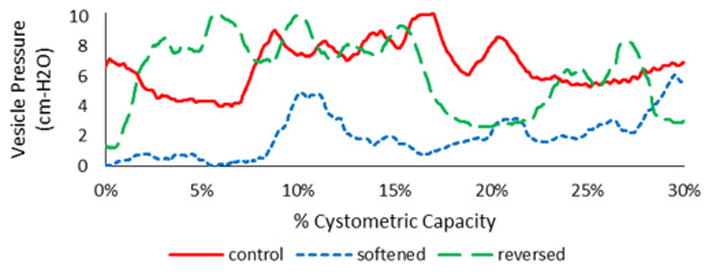
Example vesical pressure data for a volume range of 0–30% of cystometric capacity from a comparative-fill urodynamics protocol (Colhoun, Klausner et al. 2016). The “control” fill was completed following a fill to capacity and an active void. The subsequent “softened” fill was completed following a fill to 60% of capacity and passive emptying via syringe aspiration. The subsequent “reversed” fill was completed following a fill to capacity and an active void. These data demonstrate dynamic elasticity characterized by decreased filling pressure following a fill-passive emptying cycle to soften the bladder and increased filling pressure following a fill-active void cycle to reverse strain-induced stress softening.

4.3. Study limitations

Although the present study was based data from rabbit, and not human, detrusor strips (Speich, Dosier et al. 2007), the results are consistent with a recent clinical study which demonstrated dynamic elasticity due to reversible strain-induced softening during comparative-fill urodynamics (Colhoun, Klausner et al. 2016). The preload tension data were based on a relatively small data set from three rabbit bladders (Speich, Dosier et al. 2007), but other studies have also demonstrated adjustable preload tension in rabbit, mouse, and human bladders (Speich, Borgsmiller et al. 2005, Speich, Southern et al. 2012, Colhoun, Speich et al. 2015). In addition, the data used in the present model were from loading and unloading of detrusor strips. The study could be improved by modeling new data from loading curves before and after strain-induced stress softening and after strain-induced stress softening reversal and using data from human detrusor strips.

The model developed in this study assumed a spherical bladder based on the previous modeling work by Watanabe et al., (Watanabe, Akiyama et al. 1981) and by Damaser (Damaser 1999). Andersson and Arner stated that an “assumption of a spherical bladder shape, with an incompressible wall and isotropic homogeneous stretch, can give a good description of the bladder mechanics during filling” (Andersson and Arner 2004). Our model may be insufficient for bladders with significantly irregular shapes, such as a bladder with a large diverticulum.

Watanabe’s model assumed a thin-walled bladder (Watanabe, Akiyama et al. 1981), which is usually considered valid for a sphere with any inner radius to thickness ratio ≥ 10 (Hibbeler 2014). For the model results in Fig 3, the inner radius to thickness ratio was 2.7 at the initial volume of 1.5 ml. However, the inner radius to thickness ratio reached 10 at a volume of 7.2 ml, and therefore, the thin wall assumption was valid for 96% of the volume range in Fig 3.

Whole bladder dimensions were not reported for the study from which the data in Fig 1A was obtained; however, the predicted values for f in Table 2, representing the fraction of the circumference corresponding to the muscle strip length 3mm, were reasonable based on the investigator’s 18 years of experience dissecting muscle strips from rabbit bladders (Shenfeld, Morgan et al. 1998, Speich, Borgsmiller et al. 2005, Southern, Frazier et al. 2012). The bladder strips were cut in the base-to-dome direction near the dome as previously described (Almasri, Ratz et al. 2010); however bladders from a range of species include both longitudinal and circumferential layers of muscle bundles (Toosi, Nagatomi et al. 2008, Heise, Parekh et al. 2012). In most species, there are greater numbers of smooth muscle bundles running longitudinally, with two larger layers of longitudinal muscle bundles sandwiching a smaller layer of circumferential smooth muscle. In disease states such as overactive bladder, diabetes, spinal cord injury, and aging, the orientation and ratios of these layers may be altered (Hailemariam, Elbadawi et al. 1997, Burkhard, Monastyrskaya et al. 2005, Nagatomi, Toosi et al. 2005, Poladia and Bauer 2005, Schueth, Spronck et al. 2016). These structural and functional changes in the dysfunctional bladder may result in a change in material class of the bladder detrusor where the smooth muscle is preferentially hypertrophied in longitudinal layers of the detrusor (Toosi, Nagatomi et al. 2008). The directionality of the detrusor smooth muscle bundles and extracellular matrix layering may need to be taken into account in order to further refine and validate the model for detrusor behavior in diseased conditions.

The expanded Watanabe model was developed because of the relatively poor fit of Watanabe’s model at low strain for the curves in Fig 2B by simply placing two of Watanabe’s models with distinct material property parameters mechanically in parallel. It is common to compute the total strain energy of a material as the sum of the strain energies of its component materials (Boresi and Chong 2000), and, as an alternative, additional terms could have been added to the Ogden model, as previously described (Ogden 1984). The present modeling results were expected to be sufficient to predict the general trends and changes in the pressure-volume and wall-stress volume curves due to adjustable preload stiffness, and to support the conclusions of this study. A more advanced model may be necessary for certain applications, such as the model by Robod et al.(Rubod, Brieu et al. 2012) that explored the complex interaction between pelvic organs.

5. Conclusions

Several studies have demonstrated that reversible strain-induced stress softening is responsible for adjustable preload tension in detrusor smooth muscle (Speich, Borgsmiller et al. 2005, Speich, Dosier et al. 2007, Speich, Southern et al. 2012, Colhoun, Speich et al. 2015). In the present study, a hyperelastic continuum model for the bladder (Watanabe, Akiyama et al. 1981) was expanded and utilized to predict that the range of adjustable preload stress (normalized tension) versus strain curves observed in smooth muscle strips (Fig 2) would cause a substantial range of relatively flat pressure-volume filling curves and nonlinear wall stress-volume curves during filling (Fig 3). The model is consistent with a recent clinical study demonstrating dynamic elasticity during comparative-fill urodynamics (Colhoun, Klausner et al. 2016). The model results support the conclusions that 1) wall stress (but not necessarily pressure) increases throughout filling and therefore may be a better indicator of the load on the mechanosensors responsible for bladder sensation, 2) a potential defect in the acute regulation of bladder elasticity could contribute to a significant change in wall stress for a given volume that could lead to urgency, and 3) that a single urodynamic fill may be insufficient to characterize bladder biomechanics.

Highlights.

  • A continuum model was used to explore acute dynamic elasticity of the bladder

  • Modeling predicts rising wall tension during filling with little change in pressure

  • Measuring wall stress in addition to pressure could add value to urodynamics

  • Comparative-fill urodynamics are needed to elucidate complex bladder biomechanics

Acknowledgments

6. Funding

Funding for this study was provided by the Virginia Commonwealth University Presidential Research Quest Fund and NIH grant R01DK101719.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting galley proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Almasri AM, Ratz PH, Bhatia H, Klausner AP, Speich JE. Rhythmic contraction generates adjustable passive stiffness in rabbit detrusor. J Appl Physiol. 2010;108(3):544–553. doi: 10.1152/japplphysiol.01079.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Almasri AM, Ratz PH, Speich JE. Length adaptation of the passive-to-active tension ratio in rabbit detrusor. Ann Biomed Eng. 2010;38(8):2594–2605. doi: 10.1007/s10439-010-0021-7. [DOI] [PubMed] [Google Scholar]
  3. Andersson KE, Arner A. Urinary bladder contraction and relaxation: physiology and pathophysiology. Physiol Rev. 2004;84(3):935–986. doi: 10.1152/physrev.00038.2003. [DOI] [PubMed] [Google Scholar]
  4. Boresi AP, Chong KP. Elasticity in engineering mechanics. New York: Wiley; 2000. [Google Scholar]
  5. Boubaker MB, Haboussi M, Ganghoffer JF, Aletti P. Predictive model of the prostate motion in the context of radiotherapy: A biomechanical approach relying on urodynamic data and mechanical testing. J Mech Behav Biomed Mater. 2015;49:30–42. doi: 10.1016/j.jmbbm.2015.04.016. [DOI] [PubMed] [Google Scholar]
  6. Burkhard FC, Monastyrskaya K, Studer UE, Draeger A. Smooth muscle membrane organization in the normal and dysfunctional human urinary bladder: a structural analysis. Neurourol Urodyn. 2005;24(2):128–135. doi: 10.1002/nau.20103. [DOI] [PubMed] [Google Scholar]
  7. Colhoun AF, Klausner AP, Nagle AS, Carroll AW, Barbee RW, Ratz PH, Speich JE. A pilot study to measure dynamic elasticity of the bladder during urodynamics. Neurourol Urodyn. 2016 doi: 10.1002/nau.23043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Colhoun AF, Speich JE, Dolat MT, Habibi JR, Guruli G, Ratz PH, Barbee RW, Klausner AP. Acute length adaptation and adjustable preload in the human detrusor. Neurourol Urodyn. 2015 doi: 10.1002/nau.22820. [DOI] [PubMed] [Google Scholar]
  9. Damaser MS. Whole bladder mechanics during filling. Scand J Urol Nephrol Suppl. 1999;201:51–58. discussion 76–102. [PubMed] [Google Scholar]
  10. Frenkl TL, Railkar R, Palcza J, Scott BB, Alon A, Green S, Schaefer W. Variability of urodynamic parameters in patients with overactive bladder. Neurourol Urodyn. 2011;30(8):1565–1569. doi: 10.1002/nau.21081. [DOI] [PubMed] [Google Scholar]
  11. Gregersen H, Emery JL, McCulloch AD. History-dependent mechanical behavior of guinea-pig small intestine. Ann Biomed Eng. 1998;26(5):850–858. doi: 10.1114/1.109. [DOI] [PubMed] [Google Scholar]
  12. Hailemariam S, Elbadawi A, Yalla SV, Resnick NM. Structural basis of geriatric voiding dysfunction. V. Standardized protocols for routine ultrastructural study and diagnosis of endoscopic detrusor biopsies. J Urol. 1997;157(5):1783–1801. [PubMed] [Google Scholar]
  13. Heise RL, Parekh A, Joyce EM, Chancellor MB, Sacks MS. Strain history and TGF-beta1 induce urinary bladder wall smooth muscle remodeling and elastogenesis. Biomech Model Mechanobiol. 2012;11(1–2):131–145. doi: 10.1007/s10237-011-0298-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hibbeler RC. Mechanics of materials. Upper Saddle River, N.J: Prentice Hall; 2014. [Google Scholar]
  15. Holzapfel GA. Nonlinear solid mechanics: a continuum approach for engineering. Chichester, New York: Wiley; 2000. [Google Scholar]
  16. Janz RF, Kubert BR, Pate EF, Moriarty TF. Effect of Shape on Pressure-Volume Relationships of Ellipsoidal Shells. American Journal of Physiology. 1980;238(6):H917–H926. doi: 10.1152/ajpheart.1980.238.6.H917. [DOI] [PubMed] [Google Scholar]
  17. Jiang H, Liao D, Zhao J, Wang G, Gregersen H. Contractions reverse stress softening in rat esophagus. Ann Biomed Eng. 2014;42(8):1717–1728. doi: 10.1007/s10439-014-1015-7. [DOI] [PubMed] [Google Scholar]
  18. Kanai A, Andersson KE. Bladder afferent signaling: recent findings. J Urol. 2010;183(4):1288–1295. doi: 10.1016/j.juro.2009.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Levin RM, Longhurst PA, Kato K, McGuire EJ, Elbadawi A, Wein AJ. Comparative physiology and pharmacology of the cat and rabbit urinary bladder. J Urol. 1990;143(4):848–852. doi: 10.1016/s0022-5347(17)40115-7. [DOI] [PubMed] [Google Scholar]
  20. Levin RM, Monson FC, Longhurst PA, Wein AJ. Rabbit as a model of urinary bladder function. Neurourol Urodyn. 1994;13(2):119–135. doi: 10.1002/nau.1930130205. [DOI] [PubMed] [Google Scholar]
  21. Mahfouz W, Al Afraa T, Campeau L, Corcos J. Normal urodynamic parameters in women: part II--invasive urodynamics. Int Urogynecol J. 2012;23(3):269–277. doi: 10.1007/s00192-011-1585-y. [DOI] [PubMed] [Google Scholar]
  22. Matsumoto S, Chichester P, Bratslavsky G, Kogan BA, Levin RM. The functional and structural response to distention of the rabbit whole bladder in vitro. J Urol. 2002;168(6):2677–2681. doi: 10.1097/01.ju.0000031092.06002.62. [DOI] [PubMed] [Google Scholar]
  23. Mullins L, Tobin NR, Harwood JAC, Payne AR. Stress softening in rubber vulcanizates -- 3. Journal of Applied Polymer Science. 1966;10(2):315–324. doi: 10.1002/app.1966.070100212. [DOI] [Google Scholar]
  24. Murphy RA. Comprehensive Physiology. John Wiley & Sons, Inc; 2011. Mechanics of Vascular Smooth Muscle. [Google Scholar]
  25. Nagatomi J, Toosi KK, Grashow JS, Chancellor MB, Sacks MS. Quantification of bladder smooth muscle orientation in normal and spinal cord injured rats. Ann Biomed Eng. 2005;33(8):1078–1089. doi: 10.1007/s10439-005-5776-x. [DOI] [PubMed] [Google Scholar]
  26. Ogden RW. Non-linear elastic deformations. Chichester, New York, E. Horwood: Halsted Press; 1984. [Google Scholar]
  27. Poladia DP, Bauer JA. Functional, structural, and neuronal alterations in urinary bladder during diabetes: investigations of a mouse model. Pharmacology. 2005;74(2):84–94. doi: 10.1159/000083962. [DOI] [PubMed] [Google Scholar]
  28. Ratz PH, Speich JE. Evidence that actomyosin cross bridges contribute to “passive” tension in detrusor smooth muscle. Am J Physiol Renal Physiol. 2010;298(6):F1424–1435. doi: 10.1152/ajprenal.00635.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Rubod C, Brieu M, Cosson M, Rivaux G, Clay JC, de Landsheere L, Gabriel B. Biomechanical properties of human pelvic organs. Urology. 2012;79(4):968 e917–922. doi: 10.1016/j.urology.2011.11.010. [DOI] [PubMed] [Google Scholar]
  30. Saito T, Oki F. The strain-energy density function of the urinary bladder. Tohoku J Exp Med. 1982;137(4):401–408. doi: 10.1620/tjem.137.401. [DOI] [PubMed] [Google Scholar]
  31. Schueth A, Spronck B, van Zandvoort MA, van Koeveringe GA. Age-related changes in murine bladder structure and sensory innervation: a multiphoton microscopy quantitative analysis. Age (Dordr) 2016;38(1):17. doi: 10.1007/s11357-016-9878-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Shenfeld OZ, Morgan CW, Ratz PH. Bethanechol activates a post-receptor negative feedback mechanism in rabbit urinary bladder smooth muscle. J Urol. 1998;159(1):252–257. doi: 10.1016/s0022-5347(01)64077-1. [DOI] [PubMed] [Google Scholar]
  33. Southern JB, Frazier JR, Miner AS, Speich JE, Klausner AP, Ratz PH. Elevated steady-state bladder preload activates myosin phosphorylation: detrusor smooth muscle is a preload tension sensor. Am J Physiol Renal Physiol. 2012;303(11):F1517–1526. doi: 10.1152/ajprenal.00278.2012. [DOI] [PubMed] [Google Scholar]
  34. Speich JE, Borgsmiller L, Call C, Mohr R, Ratz PH. ROK-induced cross-link formation stiffens passive muscle: reversible strain-induced stress softening in rabbit detrusor. Am J Physiol Cell Physiol. 2005;289(1):C12–21. doi: 10.1152/ajpcell.00418.2004. [DOI] [PubMed] [Google Scholar]
  35. Speich JE, Dosier C, Borgsmiller L, Quintero K, Koo HP, Ratz PH. Adjustable passive length-tension curve in rabbit detrusor smooth muscle. J Appl Physiol. 2007;102(5):1746–1755. doi: 10.1152/japplphysiol.00548.2006. [DOI] [PubMed] [Google Scholar]
  36. Speich JE, Quintero K, Dosier C, Borgsmiller L, Koo HP, Ratz PH. A mechanical model for adjustable passive stiffness in rabbit detrusor. J Appl Physiol. 2006;101(4):1189–1198. doi: 10.1152/japplphysiol.00396.2006. [DOI] [PubMed] [Google Scholar]
  37. Speich JE, Southern JB, Henderson S, Wilson CW, Klausner AP, Ratz PH. Adjustable passive stiffness in mouse bladder: regulated by Rho kinase and elevated following partial bladder outlet obstruction. Am J Physiol Renal Physiol. 2012;302(8):F967–976. doi: 10.1152/ajprenal.00177.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Toosi KK, Nagatomi J, Chancellor MB, Sacks MS. The effects of long-term spinal cord injury on mechanical properties of the rat urinary bladder. Ann Biomed Eng. 2008;36(9):1470–1480. doi: 10.1007/s10439-008-9525-9. [DOI] [PubMed] [Google Scholar]
  39. Watanabe H, Akiyama K, Saito T, Oki F. A finite deformation theory of intravesical pressure and mural stress of the urinary bladder. Tohoku J Exp Med. 1981;135(3):301–307. doi: 10.1620/tjem.135.301. [DOI] [PubMed] [Google Scholar]

RESOURCES