Flexible Fitting of Atomic Models into Cryo-EM Density Maps Guided by Helix Correspondences

Abstract

Although electron cryo-microscopy (cryo-EM) has recently achieved resolutions of better than 3 Å, at which point molecular modeling can be done directly from the density map, analysis and annotation of a cryo-EM density map still primarily rely on fitting atomic or homology models to the density map. In this article, we present, to our knowledge, a new method for flexible fitting of known or modeled protein structures into cryo-EM density maps. Unlike existing methods that are guided by local density gradients, our method is guided by correspondences between the α-helices in the density map and model, and does not require an initial rigid-body fitting step. Compared with current methods on both simulated and experimental density maps, our method not only achieves greater accuracy for proteins with large deformations but also runs as fast or faster than many of the other flexible fitting routines.

Introduction

In recent years, electron cryo-microscopy (cryo-EM) has established itself as a mainstream technique to capture the structure of large macromolecular assemblies at near-native conditions (1). Although the number of density maps deposited in the Electron Microscopy Data Bank (EMDB) has grown rapidly (2), the vast majority of cryo-EM data remains at resolutions worse than 5 Å. At such resolutions, direct model building is impossible. Analysis of these nonatomic resolution density maps often relies on the availability of known or related protein structures solved by other techniques (3).

Fitting of atomic models into density maps is perhaps the most widely used method to study the structure and functional mechanisms in macromolecular assemblies captured by cryo-EM. Early attempts focused on searching for the optimal position and orientation of a target structure that best overlaps with the cryo-EM density map (4, 5, 6, 7, 8). When fitting multiple rigid-body components or domains into one density map, the search space for conformation becomes larger and different optimization methods were introduced (9, 10, 11, 12). Although important for understanding the structure and function of macromolecular complexes, rigid-body fitting is insufficient to capture conformational changes between atomic-resolution models and target density maps captured by cryo-EM (13). To overcome this limitation, various flexible-fitting methods have been introduced.

The first class of flexible fitting methods generates various conformations of proteins by numerically solving the dynamic system using molecular force fields. Different biasing forces are integrated to enforce the fitting (14, 15, 16, 17, 18, 19, 20, 21). Another class of methods is based on normal mode analysis. These methods consider the macromolecular system as an elastic network or harmonic spring-mass system around the conformation equilibrium (22), where the spring constants can be represented by chemical interactions (23). The conformational change can either be computed by importance sampling (24) or guided by the atoms’ potential collective motion directions, which are represented by low frequency modes of the dynamic system and can be computed analytically (25, 26, 27, 28). Recently, improved fitting results have been reported by combining different flexible fitting methods (29, 30).

Existing flexible fitting methods primarily rely on the density gradient around an initial positioning of the model in the map to drive the fitting process. As such, these methods require a good initial rigid-body fitting of the model to the map. A poor initial fit, where the local density gradients are not informative enough to pull the model toward the goal position, will not only result in prolonged fitting time but also may produce poor final fits due to the rugged energy landscape. Obtaining a good initial fitting is particularly challenging, if not impossible, for proteins that exhibit large conformational changes.

In this article, we present, to our knowledge, a novel flexible-fitting method for cryo-EM maps at intermediate resolutions (4–10 Å). Our key idea is to guide the fitting by the correspondence between the α-helices in the cryo-EM map and those in the model. In contrast to local gradient density, helix correspondence offers a long-range guidance that allows our method to avoid the need for an initial fitting step, improve fitting accuracy when large conformational changes are present, and achieve significantly shorter fitting times than most existing methods. Although secondary structure elements (SSEs) in models have been previously incorporated as extra constraints to maintain local geometry (stereochemistry) and accelerate fitting (24, 31, 32, 33, 34), matching of SSEs with those in a cryo-EM map has not been exploited in flexible fitting.

Our method builds upon robust methods for detecting α-helices from cryo-EM maps at intermediate resolutions (35) and for matching them with those in a template structure (36). We incorporate the helix guidance within a quadratic energy function, adapted from the computer animation community (37), which penalizes nonaffine distortion of the protein backbone. Unlike typical nonconvex energy functions used in current fitting methods, our energy function can be efficiently optimized by solving a system of linear equations. In testing our methods on both simulated and experimental cryo-EM density maps, our method achieves comparable accuracy to existing methods (typically <3 Å root mean-squared deviation (RMSD) from ground-truth structures) but runs in seconds, instead of minutes or hours, on a commodity CPU. Moreover, our method produces better fitted results than mainstream flexible fitting methods such as Flex-EM (20) and MDFF (19) when there is a significant difference between the template structure and the density map. Perhaps most importantly, our method does not require any initial rigid-body fitting.

Materials and Methods

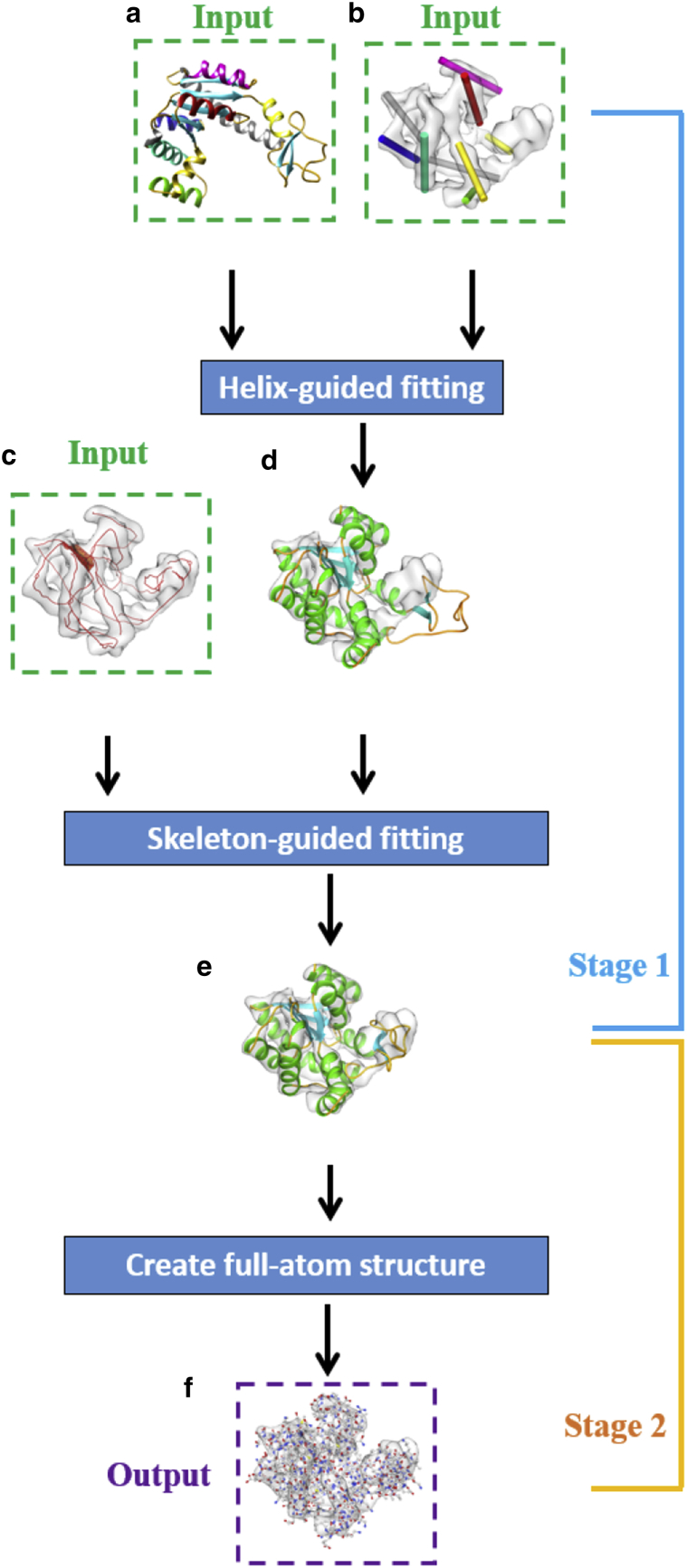
Our flexible fitting method takes as input an atomic structure (called the “model”) and a cryo-EM density map (called the “map”). To prepare for fitting, we first detect α-helices in the map (Fig. 1 b), match them to those in the model, and create the density skeleton of the map (Fig. 1 c), all using existing methods. Unlike existing flexible fitting methods, no initial rigid-body fitting or registration of the model to the map is required. Our fitting method proceeds in two stages, first fitting the C-α backbone and, second, recovering the locations of individual atoms. Our primary novelty, to our knowledge, lies in the first stage, which utilizes the helix correspondences as well as the density skeleton. This process is illustrated in Fig. 1. In the following, we first describe the preparation for fitting, followed by details on the two-stage fitting process.

Figure 1.

Overview of our method for fitting Adenylate kinase. The atomic model (PDB: 4AKE, chain A) is fitted to a simulated density map (generated from PDB: 1AKE, chain A). Our inputs are marked in green dashed boxes, including the atomic model (a), the density map with detected α-helices (b), the correspondence between the model helices and map helices (shown by coloring in (a) and (b)), and the density skeleton of the map (c). Our method consists of two stages. Stage 1 deforms the C-α backbone, which proceeds by first fitting the backbone to the map helices (d) and then to the density skeleton (e). Stage 2 recovers the full-atom structure (f), which is the output, marked in the purple dashed box. To see this figure in color, go online.

Preparing for fitting

A variety of methods can detect α-helices in a cryo-EM density map. Here, we use the software SSEHunter (35), which detects both α-helices and β-sheets using a combination of density skeletonization, local geometry calculations, and a template-based search. With SSEHunter, the detection of α-helices was shown to be highly accurate at intermediate resolutions. The method produces helices represented as three-dimensional cylinders (see Fig. 1 b). A by-product of the method is a density skeleton, computed using a thinning algorithm (38), which captures tubular and platelike density regions, respectively, by curves and surfaces (see Fig. 1 c). Our fitting method utilizes both the detected helices and the density skeleton as guidance.

Another key input to our method is the correspondence between the detected α-helices in the map and those predicted in the model. Corresponding helices should have similar lengths, close-by helices in the model should match to close-by helices in the map, and the matching should correspond to a deformation of the model that is as rigid as possible. These goals can be formulated either as a clique-finding problem (39) or a graph-matching problem (36). We use the recent graph-matching method (36), which is both more efficient and accurate. An example result is shown in Fig. 1, a and b, where corresponding helices share the same color. We used an implementation of the matching algorithm in the graphical molecular modeling software, Gorgon (40). The Gorgon implementation additionally allows the user to interactively correct any errors made by the automated algorithm. Due to possible errors in helix detection or prediction, the correspondences may only exist for a subset of the detected or predicted helices. However, a complete correspondence is not required for our fitting method; performance of our method with an incomplete helical match will be analyzed later.

Stage 1: C-α fitting

Our goal in this stage is to deform the model such that its helices are aligned with their corresponding helices in the map and that the rest of the model stays close to the density skeleton. This is achieved in two steps. Because only helix correspondences are known, we first deform the model to fit the helices (see Fig. 1 d). This initial fitting would bring the rest of the model close to the density skeleton, which guides in the refinement of fitting in the second step (see Fig. 1 e).

Both steps are formulated as a least-square minimization problem whose objective function has the following form:

$$E=w_{\text{fit}}{E}_{\text{fit}}+w_{\text{shape}}{E}_{\text{shape}}.$$ (1)

Here, w_fit and w_shape are balancing weights. E_fit measures the fitting error of the backbone to the target, the latter being either the corresponding helices (in step 1) or the combination of corresponding helices and density skeleton (in step 2). In both steps, E_fit is expressed as the sum of squared Euclidean distances between the fitted locations of a subset of C-α atoms, known as “handles”, to their target locations. E_shape measures the distortion of the protein geometry. To reduce computational cost, we adopt a simplified distortion measure that calculates the amount of nonaffine deformation in the backbone. Following Sorkine et al. (37), we express E_shape as the change in the Laplacian vector, which is the vector from each C-α atom to the centroid of its neighboring C-α atoms (given some definition of the neighborhood), between the initial model and the fitted model. We adopt the least-square technique in Sorkine et al. (37) to calculate vector difference in a rotation-independent manner (see Supporting Material). The objective function E is a quadratic function of the C-α atom locations, which can be minimized efficiently by solving a system of linear equations.

In the following, we detail the definition of C-α handles and their target locations (for constructing E_fit) as well as the definition of the C-α neighborhood (for constructing E_shape) in each of the two steps.

Stage 1, step 1: helix-guided fitting

In this step, the fitting term (E_fit) measures the deviation of the deformed model helices from their corresponding helices in the map. We consider any C-α atom in a model helix as a handle, if the helix has a corresponding helix in the map. Note that our input correspondences are of the helices, and we still need to find the target location of individual C-α handles. A naïve solution would be to compute a rigid-body transformation from a model helix to its corresponding map helix. However, due to the extra degree of freedom (rotation around the axis of the helix), solving for such a transformation is an ill-posed problem. To regularize the problem, we instead seek a transformation that optimally (in the least-square sense) aligns each model helix and its nearby helices to their corresponding map helices.

Specifically, suppose the model has k α-helices. For the ith model helix, we first determine its two end locations, {p_i,q_i}. This is done by projecting the first and last C-α atoms of the helix onto the principle eigenvector of the covariance matrix of all C-α atoms of the helix. Let {p′_i,q′_i} be corresponding end points of the helix detected in the map. We seek a rigid-body transformation matrix, M_i, that minimizes the following alignment error:

$${\sum }_{j=1}^k{w}_{ij}\left({\Vert p_j^{\prime }-M_i{p}_j\Vert }_2^2+{\Vert q_j^{\prime }-M_i{q}_j\Vert }_2^2\right),$$ (2)

where w_ij is a Gaussian that falls off with increasing distance from the ith helix, as follows:

$$w_{ij}=\exp \left(-\frac{{\Vert c_i-c_j\Vert }_2^2+{\Vert c_i^{\prime }-c_j^{\prime }\Vert }_2^2}{2{\sigma }^2}\right),$$ (3)

and where c_i,c_i′ values are, respectively, the midpoint location of the ith model helix and its corresponding map helix. We use σ = 0.1 × min(sbbd,tbbd), where sbbd and tbbd are the bounding box diagonals of source helices and target helices, respectively. The transformation M_i that minimizes Eq. 2 can be found using the method of singular value decomposition (41). For each C-α atom in the ith helix, say v, its target location is then computed as M_iv. Fig. 2, b and c, shows an example of C-α handles and their target locations.

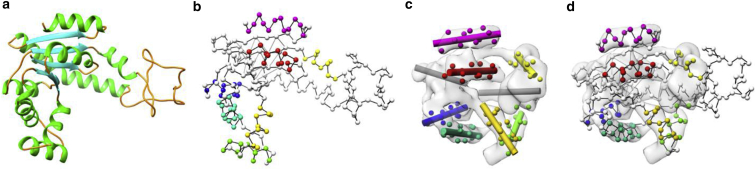
Figure 2.

Illustration of helix-guided fitting of C-α backbone. Shown are Adenylate kinase (PDB: 4AKE, chain A) (a), its C-α graph (b) where the handle C-α atoms are colored according to their corresponding helices, the target locations of the handles in the density map generated from Adenylate kinase (PDB: 1AKE, chain A) (c), and the deformed C-α graph (d). Note that the C-α graph contains edges that connect hydrogen-bonded C-α atoms in a β-sheet. To see this figure in color, go online.

To construct the shape term (E_fit), the key is to identify C-α atoms that are in the neighborhood of a given C-α atom. The shape of this neighborhood is captured by the Laplacian vector and will be protected against nonlinear distortion. Our goal is to protect the protein backbone geometry and the secondary structures (particularly the β-sheets). To do so, we create a C-α graph whose nodes are C-α atoms and each edge connects either two consecutive C-α atoms on the backbone or two hydrogen-bonded C-α atoms in a β-sheet (see Fig. 2 b).

A natural way to define the neighborhood of each C-α atom v would be the set of C-α atoms connected to v by an edge in the aforementioned C-α graph. We call this set the one-ring neighbors of v. The same definition is used in computer animation for deforming surface meshes (37). However, in contrast to the edge graph of a typical surface mesh (where each vertex on average has six outgoing edges), the one-ring neighborhood in a C-α graph is much smaller. E.g., a C-α atom along a loop segment only has two atoms in its two-ring neighborhood, whereas a C-α atom on a β-strand has only three neighboring atoms. Penalizing changes in the Laplacian vector of such small neighborhoods may not be enough to protect the shape of the protein, particularly in the loop and sheet regions.

To better protect the protein shape, we expand the neighborhood by including those C-α atoms that are connected to v via a chain of no more than r edges in the graph. We call this set the r-ring neighbors. The value of r controls the flexibility of deformation: increasing the value r leads to larger neighborhood sizes captured by the Laplacian vector, which in turn leads to deformations that appear more globally affine. Empirically, we found that setting r = 10 yields low-distortion deformations without overly limiting the flexibility of fitting.

We use the setting w_fit = 1 and w_shape = 1 for this step. Because the two terms, fitting and shape, are not measured on the same scale, this setting in fact puts more emphasis on fitting. We show the effect of different weight settings on the fitting results in the Supporting Material.

Stage 1, step 2: helix- and skeleton-guided fitting

After the first step of helix-guided fitting, the model is usually deformed to lie in the vicinity of the target density. In the second step, we refine the fitting by pulling the model toward the local maxima of density (i.e., the density skeleton) while preserving the protein geometry.

We modify the fitting term (E_fit) in step 1 by adding a second set of handles that comprise all those C-α atoms that are not considered as handles in step 1. To pull the model toward the density skeleton, the key task is to identify the target locations of these new handles on the skeleton. A naïve choice would be the Euclidean closest points. However, such a choice can be suboptimal when the C-α atom is far from the skeleton. To make a better choice, we apply the classical iterative closest point method (42), which alternates between deforming the backbone and updating the target locations as closest points. We start by finding the nearest point on the skeleton, say p, to the current location of each C-α atom, say v. Assigning p as the target location of v, we then compute the deformation by solving Eq. 1. This process is iterated until a convergence criteria is met. In our implementation, we stop the iterations when the RMSD between the models generated in two successive iterations is below a certain threshold (we use 0.1 Å). When searching for the nearest point for a C-α atom in a loop (respectively, β-strand) segment, preference is given to points on the curve (respectively, surface) region of the skeleton. To improve accuracy, we only consider those C-α atoms whose nearest skeleton point is <10 Å away.

We use the same shape terms (E_shape) as in step 1. To avoid overfitting to the skeleton geometry, we use w_fit = 1 and w_shape = 1.

Stage 2: recovering atom positions

To recover all atom locations, we transform each residue on the model as a single rigid group based on the deformation of the C-α atoms. The transformation is computed as one that best aligns the C-α atoms of the current and neighboring residues on the backbone to their deformed locations. Specifically, let v_i,v_i′, be the original and deformed locations of the C-α atom of the ith residue in the primary sequence. We seek the rigid-body transformation, A_i, for the ith residue that minimizes the error, as follows:

$${\sum }_{j=i-f}^{i+f}{\Vert v_j^{\prime }-A_i{v}_j\Vert }_2^2,$$ (4)

where f is a user-specified constant that controls the rigid-body neighborhood range for each residue. We use f = 3 to balance the stability and the flexibility of the transformation. The minimizing A_i value can be solved using the method of singular value decomposition (41).

Results

Our method was implemented as a plugin to Gorgon (http://gorgon.wustl.edu), an open-source protein and molecular modeling/visualization suite. With this plugin, we evaluated the accuracy and efficiency of our proposed method using data sets with both simulated and experimentally determined density maps.

Unlike most flexible fitting methods, our method does not need an initial rigid-body fitting as the starting model. However, for evaluation purposes, we do a rigid-body fitting of the source model into the target density map using the helix correspondences. This rigid-body fit serves only as a baseline for comparison and is not used in our flexible fitting method. Specifically, we formulate the rigid-body transformation as the one that optimally aligns the model helices to their corresponding helices in the density map. It is found by minimizing a quadratic error function similar to that in Eq. 2, except w_ij = 1 for any i,j.

Simulated density maps

We selected six pairs of proteins from the PDB, which have been used to evaluate other protein fitting methods (43, 44). The selected protein pairs have identical or nearly identical amino acid sequences (98.86–100% similarity) but exhibit a wide variety of collective conformational changes. The helix content ranges between 40 and 60% in these proteins. For each pair, a density map was simulated from one of the proteins (the target model) at the resolution of 9 Å using EMAN2 (45). We then fit the other protein (the source model) to the simulated map. The information of the data set is summarized in Table 1.

Table 1.

Summary of the Data Set in which the Density Maps Are Simulated

Dataa Set ID	Source Model					Target Model					Sequenceg Identity (%)
	Protein Nameb	PDB IDc	Residued ID	Lengthe (Amino Acids)	Helix Residuesf Percentge	Protein Name	PDB ID	Residue ID	Length (Amino Acids)	Helix Residues Percentage
1	Adenylate kinase	4AKE [A]	1–214	214	0.459	Adenylate kinase	1AKE [A]	1–214	214	0.593	100.00
2	Triacylglycerol acylhydrolase	3TGL [A]	5–269	265	0.4	Triacylglycerol acylhydrolase	4TGL [A]	5–269	264	0.381	98.86
3	Maltodextrin binding protein	1OMP [A]	1–369	369	0.513	Maltodextrin binding protein	1ANF [A]	1–369	369	0.459	100.00
4	Aspartate aminotransferase	9AAT [A]	3–410	401	0.476	Aspartate aminotransferase	1AMA [A]	3–410	401	0.506	100.00
5	GroEL	1OEL [A]	2–525	524	0.534	60 kDa chaperonin	2C7C [A]	2–525	524	0.595	99.23
6	Lactoferrin	1LFG [A]	1–691	691	0.421	Lactoferrin	1LFH [A]	1–691	691	0.421	99.69

^aThe data we use in each test.

^bProtein name.

^cProtein PDB ID and chain ID.

^dThe amino acid residues we use to evaluate RMSDs.

^eThe number of amino acid residues in the sequence.

^fThe percentage of helix residues.

^gThe sequence identity between the source model and target model.

We examined the fitting accuracy by calculating the RMSD between the target models and the source models fitted by rigid-body fitting, flexible fitting with only helix guidance (Stage 1, Step 1), and flexible fitting using both helix and skeleton guidance (Stage 1, Step 2) (see Table 2). In the following results and tables, the RMSD is computed only between matching residues in the source and target models (residue ranges are shown in Table 1). For all protein pairs, our method achieved a C-α atoms RMSD of 2.8 Å or less, which is comparable to previously reported results (15, 26, 46). Furthermore, even though we use helices as the primary guidance of fitting, we still achieve comparable fitting quality for nonhelical components such as strands and loops (see breaking-down of the RMSD into secondary structure elements in Table 2), thanks to the use of density skeletons. All-atom RMSD are reported in the Supporting Material (see Table S2). Also shown in Table 2 are the cross-correlation scores, calculated using the software UCSF Chimera (34), comparing the density maps simulated from the fitted source models against the density maps simulated from the target models. Our flexible fitting method significantly improves the correlation over rigid-body fitting.

Table 2.

Accuracy of Fitting Source Models to Simulated Density Maps Generated at 9 Å Resolution from the Target Models

Data Set	RMSD (Å)						Cross-Correlation Score
	Rigida Fitting	Helix-Guidedb Fitting	Helix-and-Skeleton-Guided Fittingg
			Allc Residues	Identifiedd Helix Residues	Strandse Residues	Loopf Residues	Rigid Fitting	Helix-and-Skeleton-Guided Fitting	Densityh Level	Densityi Level Range
Adenylate kinase	11.317	5.503	2.865	2.651	2.572	3.546	0.7675	0.9176	0.0643	0–0.958
Triacylglycerol acylhydrolase	12.239	2.491	1.943	1.827	1.714	2.203	0.8582	0.9488	0.0706	0–0.582
Maltodextrin binding protein	3.845	1.293	1.721	1.243	2.513	1.865	0.9361	0.9727	0.0746	0–0.521
Aspartate aminotransferase	7.435	2.247	1.082	0.934	0.723	1.379	0.8579	0.9756	0.0681	0–0.535
GroEL	15.983	3.041	2.488	2.531	2.336	2.487	0.7286	0.9646	0.0618	0–0.517
Lactoferrin	6.739	1.732	1.625	1.202	1.560	2.041	0.9114	0.968	0.0771	0–0.538

^aThe metrics include RMSD of all the residues between the target model and the fitted source model using rigid-body fitting.

^bHelix-guided fitting.

^cHelix-and-skeleton-guided fitting.

^dRMSD of identified helix residues.

^eStrand residues.

^fLoop residues between the target model and the fitted source model using helix-and-skeleton-guided fitting.

^gCross-correlation score of the rigid fitted and the helix-and-skeleton guided fitted models.

^hColumn represents the density threshold in the software Chimera we use to evaluate the cross-correlation score.

ⁱColumn represents the density level range of the simulated density map. The residue used to compute the C-α atoms RMSDs are listed in Table 1.

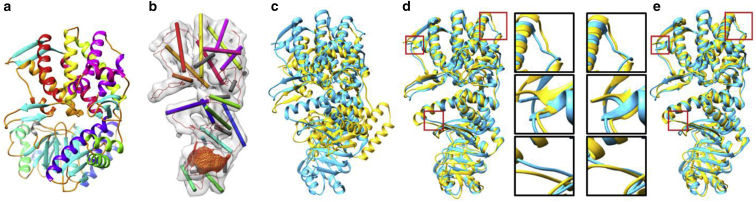
The helix-and-skeleton-guided fitting (Stage 1, Step 2) offers variable improvement over helix-guided fitting (Stage 1, Step 1). Some structures, such as Adenylate kinase (Fig. 1) and GroEL (Fig. 3), exhibit notable improvement in fitting accuracy, particularly in the loops and β-sheets. Others exhibit marginal improvement or slight degradation in accuracy. We attribute such variability to the variability in the density skeletons, such as how well the skeleton curves approximate the protein backbone and how well the skeleton surfaces characterize the β-sheets.

Figure 3.

An example where fitting guided by both helix correspondences and density skeletons improves accuracy using only helix correspondences. (a) Shown here is the source model (GroEL, PDB: 1OEL chain A), (b) target simulated density map (60 KDA chaperonin, PDB: 2C7C, chain A) with detected helices (cylinders colored by correspondences with helices in the source model) and skeletons (red curves and yellow surfaces), (c) result of rigid-body fitting, (d) result of helix-guided flexible fitting, and (e) result of helix-and-skeleton-guided flexible fitting. The fitted source models are shown in yellow and the target model is shown in cyan. The closeups examine a few regions where considering skeletons offers notable improvements. To see this figure in color, go online.

We have also observed that fitting accuracy is not strongly affected by map resolution. Table S4 reports the errors (in C-α atoms RMSD) of fitting Adenylate kinase 4 (AKE) to maps simulated from 1 AKE at resolutions ranging from 9 to 3 Å. The errors exhibit a low variation (by <0.1 Å) in the intermediate resolution range of 9–5 Å and only increases slightly (by <0.5 Å) at resolution 3 Å. The increase is mainly attributed to the errors in nonhelical residues, which are due to the unique morphology of density skeletons at near-atomic resolutions (e.g., skeleton curves may represent side chains instead of the backbone, and β-sheets become clearly visible strands that are no longer represented by the skeleton surfaces). We recognize the fact that simulated density maps do not contain the same information as experimentally derived maps at corresponding resolutions. However, simulated data does provide a systematic mechanism for assessment of our method as resolution decreases without compounding variables when trying to compare experimental maps derived from different software, imaging, and biochemical preparations. However, this general trend in accuracy versus resolution is also seen in the subsequently tested experimental maps (Tables 4, 5, 6, and 7).

Table 4.

Summary of the Data Set in which the Density Maps Are Deposited in the EMDB

Dataa Set ID	Protein Nameb	Source Model				Target Cryo-EM Map
		PDB IDc	Residue IDd	Lengthe (aa)	Helix Residuesf Percentage	EMDB Idg	Maph Resolution	Target Modeli
								PDB ID	Residue ID	Length (aa)	Helix Residues Percentage
7	Ribosome maturation protein SBDS	5AN9 [J]	1–250	250	0.468	3146	4.1	5ANB [J]	1–250	250	0.5
8	Magnesium transport protein CorA	3JCF [E]	19–349	331	0.575	6552	7.1	3JCG [A]	19–349	331	0.5
9	26s protease regulatory subunit 6b homolog	3JCO [K]	48–418	371	0.481	6575	4.6	3JCP [K]	48–418	371	0.5
10	Chaperonin	3IZH [C]	1031–1538	513	0.549	5645	4.6	3J3X [I]	11–518	510	0.6
11	60 kDa chaperonin	2C7C [M]	3–524	524	0.604	1180	7.7	2C7C [A]	3–524	524	0.6
12	DNA polymerase III subunit α	5FKV [A]	1–926, 943–1160	1160	0.58	3201	8.3	5FKU [A]	1–926, 943–1160	1160	0.5

^aThe data we use in each test.

^bProtein name.

^cProtein PDB ID and chain ID.

^dThe amino acid residues we use to evaluate RMSDs.

^eThe number of amino acid residues in the sequence.

^fThe percentage of helix residues.

^gProtein EMDB ID.

^hThe resolution of the target cryo-EM map.

ⁱThe atomic structure (deposited in PDB) of the target density map reported in EMDB. The sequence identity between the source model and the cryo-EM map’s target model are all 100%.

Table 5.

Result of Fitting the Source Models to the Experimental Target Density Cryo-EM Maps by Different Methods

Data Set	RMSD (Å)							Cross-Correlation Score						FSC Agreed Resolution (Å)
	Rigida Fitting	Flex-EMb Fitting	MDFFc Fitting	Helix-and-Skeleton-Guided Fittingh
				Alld Residues	Identifiede Helix Residues	Strandsf Residues	Loopg Residues	Rigid Fitting	Flex-EM Fitting	MDFF Fitting	Helix-and-skeleton-guided Fitting	Densityi Level	Densityj Level Range	Rigid Fitting	Flex-EM Fitting	MDFF Fitting	Helix-and-skeleton-guided Fitting
Ribosome maturation protein SBDS	19	16	15	4.782	2.100	6.840	5.837	0.6	0.7	0.75	0.8	0.6	0–1.29	35	26.1	24	18.7
Magnesium transport protein CorA	4.5	2.73	2	2.741	2.596	1.970	3.453	0.9	0.9	0.97	0.91	0.19	0–0.588	16	8.3	7	7.8
26s protease regulatory subunit 6b homolog	5.6	2.17	2	2.019	1.160	2.560	2.593	0.8	0.9	0.95	0.91	0.47	0–1.08	20	7.5	7	6.8
Chaperonin	5.1	1.53	1	1.696	1.430	1.314	1.932	0.8	0.9	0.95	0.94	0.62	0–1.07	18	6.6	6	6.8
60 kDa chaperonin	14	12.1	12	2.261	1.795	2.491	3.190	0.9	1	0.91	0.98	0.39	0–0.568	15	7.2	14	5.7
DNA polymerase III subunit α	12	13.8	13	2.757	2.480	2.109	3.310	0.9	1	0.95	0.98	0.41	0–0.547	7.4	7.5	7	6.5

^aThe reported metrics are RMSD of all the residues between the final fitted result against the target model for rigid fitting.

^bFlex-EM fitting.

^cMDFF fitting.

^dHelix-and-skeleton-guided fitting.

^eRMSD of identified helix residues.

^fStrand residues.

^gLoop residues between the target model the fitted source model using helix-and-skeleton-guided fitting.

^hCross-correlation score of the target model and the fitted models of different methods; the resolution to which the fitted models and target models agree based on the 0.5 FSC criteria.

ⁱRepresents the density threshold in the software Chimera we use to evaluate the cross-correlation score.

^jColumn represents the density level range of the target models’ simulated density map. The residue IDs used to compute the C-α atoms RMSDs are listed in Table 4.

Table 6.

Ramachandran Outliers and Clash Score of the Source Models

Data Set	Ramachandran Outliers					Clash Score
	Sourcea Model (%)	Flex-EMb Fitted Model (%)	MDFF Fittedc Model (%)	Helix-and-Skeletond-Guided Fitted Model (%)	Targete Model (%)	Source Model	Flex-EM Fitted Model	MDFF Fitted Model	Helix-and-Skeleton-Guided Fitted Model	Target Model	Refined Fittedf Model
Ribosome maturation protein SBDS	1.20	2.40	0.80	2.40	2.40	0.48	55	9.93	229	1.21	8.5
Magnesium transport protein CorA	0.00	4.30	0.00	0.90	0.00	7.75	119.8	10.2	239	0	69.4
26s protease regulatory subunit 6b homolog	1.70	2.00	0.60	2.50	3.40	81.18	218.24	12.5	274	69.29	39.5
Chaperonin	1.00	1.00	0.00	0.60	1.00	3.7	108.22	8.03	67.7	1.79	59.6
60 kDa chaperonin	0.60	2.70	0.00	1.50	0.80	0.13	287.27	11.9	128	0	43.9
DNA polymerase III subunit α	3.80	4.20	1.30	3.00	2.70	26.27	100.67	12.2	180	21.43	72.9

^aThe final fitted (helix-and-skeleton guided fitting) models.

^bFlex-EM fitted models.

^cMDFF fitted models.

^dTarget models.

^eColumn.

^fShows the clash scores of Phenix-refined models.

Table 7.

Timing of Our Method on Experimental Density Maps and Comparison with Flex-EM and MDFF

Data Set	Length (aa)	Our Method Time in Seconds					Flex-EM Time in S	MDFF Time in S
		Helix-Guided	Skeleton-Guided		All Atoms	Total
			Iterations	Time
Ribosome maturation protein SBDS	250	0.076	10	2.79	0.012	2.878	5457	639
Magnesium transport protein CorA	331	0.153	9	1.56	0.017	1.73	15,639	964
26s protease regulatory subunit 6b homolog	371	0.183	6	1.33	0.176	1.689	3081	904
chaperonin	513	0.417	5	4.01	0.024	4.451	11,026	1418
60 KDA chaperonin	524	0.471	4	2.758	0.245	3.474	10,915	1420
DNA polymerase III subunit α	1160	2.987	7	29.876	0.056	32.919	12,382	3288

From Ribosomal data set to DNA polymerase data set, the number of amino acid residues keeps increasing, as shown in column (e) of Table 4.

We next examined the structural quality of fitted models using two benchmarks: Ramachandran score and clash score. Table 3 shows the percentage of Ramachandran outliers in the source, fitted source, and target models, as well as their clash scores. Ramachandran plots of these examples can be found in Fig. S3. Our flexible fitting method maintains the local geometry of the protein well, which indicates the effectiveness of our Laplacian-based shape distortion penalty term (E_shape in Eq. 1). However, fitting increases the amount of clashes. We found that further refinement of our fitted structures using real-space refinement tools, such as Phenix (47), greatly reduces the amount of clashes. Refinement is fast to run (7–15 min in our experiments) due to the proximity of the fitted model to the density. For Phenix, we used default parameters with “simulated annealing (Cartesian)” and “simulated annealing (Torsion angles)” enabled. Each refinement runs for 3–10 cycles.

Table 3.

The Ramachandran Outliers and Clash Score of the Source Models, the Clash Score Is the Lower the Better

Data Set	Ramachandran Outliers			Clash Score
	Sourcea Model (%)	Helix-and-Skeletonb-Guided Fitted Model (%)	Targetc Model (%)	Source Model (%)	Helix-and-Skeleton-Guided Fitted Model	Target Model	Refinedd Fitted Model
Adenylate kinase	1.40	2.80	0.00	16.16	324.23	4.94	72.73
Triacylglycerol acylhydrolase	0.00	0.00	1.10	15.35	264.43	35.51	53
Maltodextrin binding protein	0.50	0.50	0.80	10.72	153.57	18.68	36.6
Aspartate aminotransferase	0.30	0.50	0.30	6.31	91.26	25.81	28.8
GroEL	0.40	1.30	0.80	15.62	149.42	0	66
Lactoferrin	1.90	3.20	2.00	23.24	191.94	28.35	40.5

^aThe final fitted (helix-and-skeleton guided fitting) models.

^bTarget models.

^cColumn.

^dShows the clash scores of Phenix-refined models.

In terms of running time, our method finished in <10 s for each protein pair. A detailed breakdown of the timing is included in Table S1. The timing is dominated by stage 1 (C-α fitting), which in turn is dominated by step 2 (helix-and-skeleton-guided fitting) due to repeated solving of the deformation and closest-point queries. All experiments were performed on a single core on a PC with a 3.60 GHz CPU (Intel Core i7-4960X; Intel, Santa Clara, CA) and 16 GB memory. We used the linear solver in Eigen (48) to solve the Laplacian-based deformation.

Experimental cryo-EM density maps

We tested our method on six experimentally determined cryo-EM density maps obtained from the EMDB whose resolutions range from 4 to 8 Å. These maps are selected to have different amounts of conformational changes between the source and the target. Each map also comes with a source model (to be fitted) and a target model (for evaluation purpose), both of which are from original coordinates deposited in RCSB/PDB. Typically, the target model for each cryo-EM density map is the “Fitted atomic model” reported in EMDB. The information about these data, including the range of matching residues and percentage of helix contents, is summarized in Table 4. The results of rigid-body fitting and our flexible fitting method for each map are shown in Fig. 4.

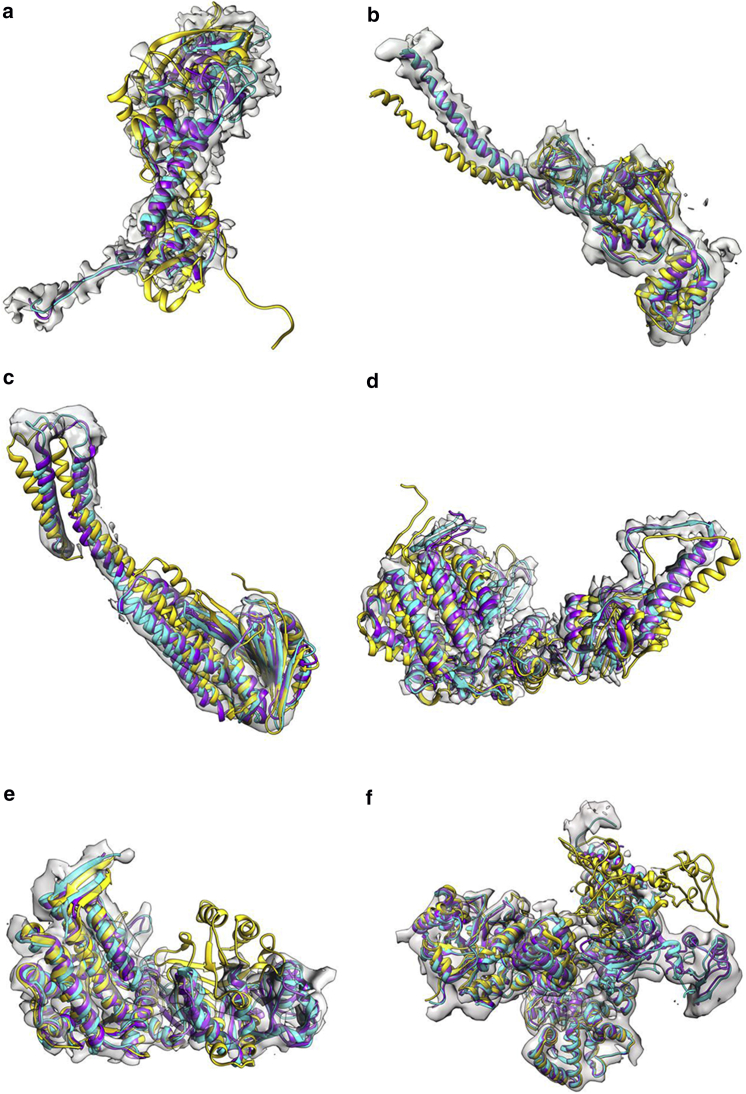
Figure 4.

The target model (cyan), the source model fitted by rigid-body fitting (yellow), and our flexible fitting method (purple) in each of our test suites with observed density maps. The represented data are: (a) ribosome maturation protein SBDS (source PDB: 5AN9 chain J, target EMDB: 3146); (b) magnesium transport protein CorA (source PDB: 3JCF chain E, target EMDB: 6552); (c) 26s protease regulatory subunit 6b homolog (source PDB: 3JCO chain K, target EMDB: 6575); (d) chaperonin (source PDB: 3IZH chain C, target EMDB: 5645); (e) 60 KDA chaperonin (source PDB: 2C7C chain M, target EMDB: 1180); and (f) DNA polymerase iii subunit α (source PDB: 5FKV chain A, target EMDB: 3201). To see this figure in color, go online.

We first examined the fitting accuracy using RMSD and cross-correlation scores (Table 5). For cross correlation, we compared the density maps simulated from the fitted models against the map simulated from the target model, both at the same resolution as the target cryo-EM maps. To compare the models, we also report the spatial resolution using the 0.5 Fourier shell correlation (FSC) criteria (49) between these simulated density maps of the models (Fig. S7). All-atom RMSDs are also reported in Table S3. For the majority of the maps, our flexible fitting achieves <2.8 Å RMSD error, >0.9 cross-correlation score, and comparable resolution-of-agreement to the target map resolution, despite the presence of large protein deformations (e.g., GroEL and DNA polymerase). We attribute the larger error of the ribosome maturation protein SBDS to a combination of factors, including a low percentage of helix residues (lowest among all data sets), an exceptionally large deformation, and unique skeleton features in a near-atomic resolution map as mentioned earlier.

The overall higher RMSD compared to our earlier experiments with simulated density maps is largely due to the increased noise and ambiguity in the observed cryo-EM density map, which results in less reliable density skeletons. Coordinate data filtered to make low-resolution maps may be significantly better (e.g., having cleaner density skeletons) than a comparable resolution experimentally produced dataset. This is evident in the slightly worse RMSD of nonhelical components, whose fitting is guided primarily by the density skeletons (as opposed to the helices, which are guided by the correspondences).

We next examined the structural quality of our fitted models in terms of their Ramachandran outliers and clash scores (Table 6). As in the data sets with simulated density maps, we see a low level of Ramachandran outliers but elevated clash scores, the latter of which can be significantly reduced after further refinement in Phenix. The Ramachandran plots can be found in Fig. S4.

We compared our method with Flex-EM (20) and MDFF (19), two commonly used and freely available flexible fitting tools. For both packages, we use the default parameters or those specified in the packages’ documentation. One complete iteration (1 CG run and 20 MD iterations in Flex-EM) were performed for each package. For detailed settings of both methods, please refer to Supporting Material; parameters for the MDFF and Flex-EM fits can also be found in the Supporting Material.

We observed that the fits using our method are comparable to those obtained from Flex-EM and MDFF when the protein undergoes small conformational changes, but significantly better for the datasets in which the protein makes large nonrigid conformational changes (e.g., ribosome maturation protein SBDS, 60 KDA chaperonin, and DNA polymerase). This is evident in all three measures (RMSD, cross-correlation scores, and FSC) reported in Table 5. In terms of model quality, the resulting models from all three methods (after real space refinement in our approach) are comparable as reflected by both the Ramachandran outliers and clash scores in Table 6.

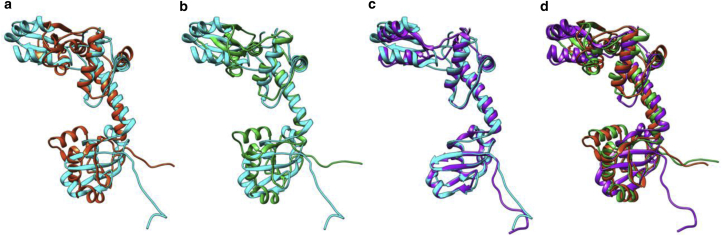
A closer look at ribosome maturation protein SBDS in Fig. 5 (and in a zoomed-in view in Fig. S5) illustrates a deformation in which fitting the initial model (PDB: 5AN9) to the target density map (EMDB: 3146) involves a large twist between the upper and lower domains. Whereas both Flex-EM and MDFF are trapped in a local minima not so far from the initial rigid-body fit, due to the lack of sufficient guidance from local density gradients, our method achieves a much more satisfactory global fit. It should be noted, however, that in some examples where such large conformational changes are present, iterative refinement strategies that involve progressive low-pass filtering of the density map have shown some level of success in capturing these conformational changes.

Figure 5.

Here we compare the result of fitting the source model (ribosome maturation protein SBDS, PDB: 5AN9 chain J) to the density map (ribosome maturation protein SBDS, EMDB: 3146) by Flex-EM (red) (a), MDFF (green) (b), and our method (purple) (c). The target model (ribosome maturation protein SBDS, PDB: 5ANB chain J) is colored cyan. (d) Shown here is the overlap of the fitted source model by Flex-EM, MDFF, and our method. A zoomed-in view can be found in Fig. S5. To see this figure in color, go online.

Besides the ability to handle large deformations, another significant advantage of our method is efficiency. As shown in Table 7, our method is faster than both Flex-EM and MDFF by at least two orders of magnitude on a single core of a modern desktop workstation. Even the largest and most complex case in our test suite (1160 residues) required <33 s. Additionally, we tested the GPU-accelerated version of MDFF (50) on the data sets 7–12 using a LINUX workstation equipped with a dedicated GPU board. Overall, we observed a 2–10 times speedup compared to CPU-only MDFF. We can see our method is still ∼10–50 times faster than GPU-accelerated MDFF. Note that both Flex-EM and MDFF require an initial rigid-body fitting stage, whose time is not included here. Our method has no such requirement.

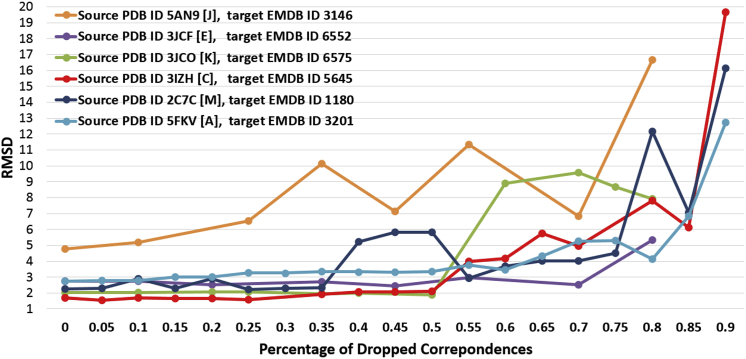
Our method is primarily guided by the matching between detected helices in the density map and those found in the template structure. Several factors could affect the robustness of both the detection and matching of helices, including density resolution and the length and linearity of helices in the map. To evaluate the dependence of our method on the quality of the helix matching, we randomly drop helix correspondences in the input and calculate the RMSD of fitting as the number of dropped correspondences increases. This is done for each of the six experimental density maps. As shown in Fig. 6, the fitting quality degrades gracefully as helix matching worsens. In most of the examples, the fitting accuracy remains high even when as much as 30% of helix correspondences are missing. We attribute this stability to the use of density skeletons as the additional guidance in our fitting.

Figure 6.

Fitting accuracy (as C-α RMSD) at increasing percentage of dropped helix correspondences. To see this figure in color, go online.

Fitting a protein complex

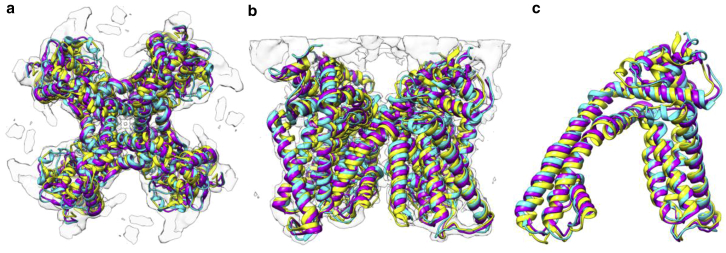
As a further test of our method on large protein complexes, we examined flexible fitting on the complete transmembrane domain of an integral membrane protein, TRPV1. We selected chain D of the transient receptor potential cation channel subfamily V member 1 protein (PDB: 3J5Q), trimmed it to the transmembrane-only region (residues 383–719), and used it as the source model to fit it into the density map of capsaicin receptor (EMDB: 5778). Because the helix-matching algorithm we adopted only supports one-to-one matching, we computed the correspondence between the helices in the source model and the helices detected from the map that belong to each of the four chains. Taking these correspondences as input, we fit the source model into the entire density map four times, each time generating one chain of the final fitted protein complex. A visualization of the fitted complex is shown in Fig. 7.

Figure 7.

The result of fitting the transmembrane domain of an integral membrane protein, TRPV1. The source model (PDB: 3J5Q chain D) is fitted to the density map (EMDB: 5778) by rigid-body fitting (yellow) and our flexible fitting method (purple), overlapping with the target model (PDB: 3J9J). (a) Shown here is the top view of the fitting result of the entire complex, (b) the side view of the fitting result of the entire complex, and (c) the zoomed-in view of the fitting result of one chain (corresponds to the target model chain A). To see this figure in color, go online.

The fitting process took only 10 s to generate the entire protein complex (four chains and 1328 residues in all). To evaluate the fitting accuracy, we took the capsaicin receptor’s (EMDB: 5778) fitted atomic model (PDB: 3J9J) using the software Rosetta (51, 52) as the target model and calculated the RMSD between the target model and our fitted model. Our method achieved a fit with <1.8 Å RMSD over the entire complex. Fig. 8 shows the comparison of the fitted model by our method and the target Rosetta model. The majority of the fitting error is localized to regions around the termini and breaks in the model. Generally, accuracy of fitting elsewhere in the maps is relatively uniform. Error also does not seem to be effected by subunit interfaces. The fitted complex has similarly high cross-correlation scores (0.78) and low Ramachandran outliers (1%) as in our other data sets (Ramachandran plots are found in Fig. S6).

Figure 8.

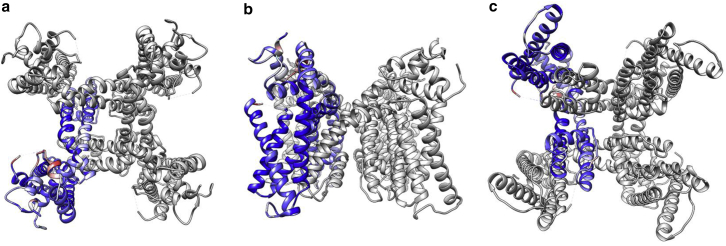
Given here is the top view (a), side view (b), and bottom view (c) of the flexibly fitting result of TRPV1 using our method. A single monomer has been colored based on the RMSD of our fitted model and the ground truth model (PDB: 3J9J). Our fitted model is colored from 0 (blue) to 6 Å RMSD (red). Overall RMSD is <2 Å. To see this figure in color, go online.

The resolution to which our fitted complex and the experimental map (EMDB: 5778) agree is 7.0 Å at a FSC cutoff of 0.5. The fitted complex has a relatively high clash score (170.81) and low EMRinger score (0.68, against experimental map). After Phenix refinement (∼30 min), we are able to obtain a much lower clash score (33.6), a higher EMRinger score (1.66, against experimental map), and a better FSC (3.7 Å). These metrics are closer to the Rosetta model (PDB: 3J9J), which has an FSC of 3.6 Å at 0.5 cutoff and an EMRinger score of 2.34. We have included all FSC plots in Fig. S8. Additional rounds of refinement and adjustment of refinement parameters would likely result in model statistics approaching those of the Rosetta model.

Discussion

In this work, we present, to our knowledge, a novel method to flexibly fit an atomic model into a cryo-EM density map determined at intermediate resolutions. Our method leverages existing tools for detecting α-helices in the density map and matches them to those in a given model. Guided by the helix correspondences and density skeletons, our method adapts a popular method in computer graphics to deform the model while preserving its shape. Results of fitting with both simulated and observed cryo-EM density maps show that our method achieves results comparable to those reported by other methods (and better in the case of large conformational changes), though with significantly faster performance (reducing compute times by at least two orders of magnitude).

The two contributors of increased performance are the use of helix correspondences, which serve as a long-range guidance, and a simple-to-minimize quadratic objective function. The combination of the two allows our method to make few but large steps toward the goal. In contrast, current methods based on molecular dynamics or normal modes typically make small conformational changes in each simulation step, which lead to slower convergence and higher sensitivity to local minima.

Although the increased performance allows the user to better explore possible fitting solutions, perhaps the biggest advantages of our method are that 1) no additional fitting is required, and 2) flexible fitting is actually guided by resolution appropriate features. With nearly all other flexible fitting methods, an initial registration of the target model in the density map is required. This localization can be potentially biased because of the intrinsic structural differences between the pose of the model in the complex. As such, models with poor initial registration in the density are more likely to fall into local minima. In terms of the flexible fitting of the source model, observable and quantifiable structural features in both the density map and the target structure guide the deformation in our approach. With other flexible fitting methods, fitting is guided either by a high-resolution energy function or an elastic model; our approach uses resolution-appropriate features to guide the fitting. As such, our flexible fitting technique is more likely to produce accurate results even when dealing with large conformational differences in the target model.

We acknowledge that methods such as MDFF are capable of dealing with large conformational differences using a multiresolution approach (53). By gradually fitting the model of interest to progressively higher resolution density maps, conformational space of the fitting can be better explored and pitfalls due to the ruggedness of the energy surface may be avoided. However, such an approach requires multiple fittings and thereby increases the time to achieve an accurate result. In addition, designing an effective protocol following such an approach often requires expertise, and the best outcomes are likely to come from more experienced users. In contrast, our method has a relatively simple design, which requires little experience or tweaking to achieve fast and accurate results.

Our Laplacian-based objective function is effective in preserving the protein shape, but it does not consider the physical and chemical constraints such as residue distances and bond angles. To improve model quality after flexible fitting, the result of our method can be further refined using existing software packages such as Phenix (47), Rosetta (54), and MDFF (19), to resolve clashes and restore proper distances and angles. Such approaches have been shown to recover correct protein stereochemistry even in the presence of fairly large errors (55, 56).

There are several directions that we would like to explore to further improve our method and expand its utility. First, this method considers only correspondences of α-helices, as they are less affected than β-sheets during conformational changes. Currently, our method would not be suitable for proteins with few or no α-helices. In the future, we plan to compute correspondences between detected β-sheets in a density map and those in a model. Once incorporated into our fitting method, these correspondences would enable us to handle a larger variety of proteins. Second, the significant gain in efficiency by using our method, compared to current methods, makes it more practical to explore multiple solutions. The ability to generate and assess an ensemble of models is important in the face of uncertainty in the map. We plan to investigate how the change of the parameters of fitting (e.g., fitting weight and neighborhood size), and the skeletons, capture the uncertainty of data.

Author Contributions

T.J. and M.L.B. designed the research. H.D., D.W.B., and T.J. performed the research, analyzed the data, and wrote the article.

Editor: Andreas Engel.