Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2017 Jun 26;7:4229. doi: 10.1038/s41598-017-04415-z

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2017

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

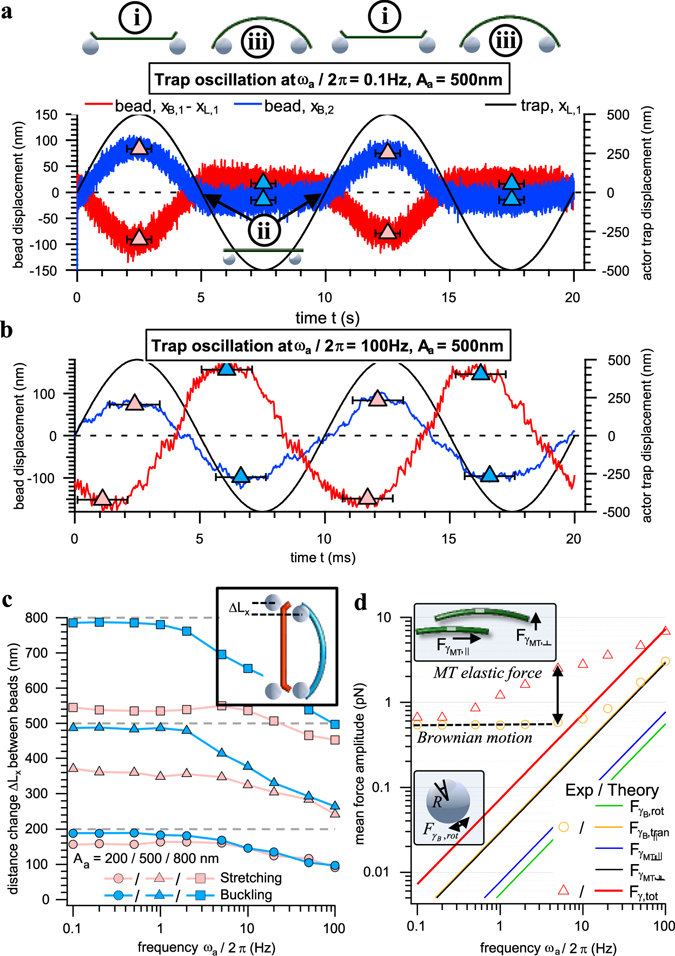
Frequency dependent response of a single microtubule filament – bead construct (L = 5 µm). (a) and (b) Two periods of the relative actor and sensor bead displacements x _B1(t) − x _L1(t) and x _B2(t) − x _L2(t) from their trap centers during oscillations of the actor trap x _L1(t) = L/2 + A _asin(ω _a t) and the static sensor trap x _L2(t) = −L/2 at A _a = 500 nm and ω _a/2π = 0.1 Hz (a), or ω _a/2π = 100 Hz (b), respectively. Markers indicate the maximum amplitude x _max1 and x _max2 of both beads during each half period. (c) Frequency dependence of the maximum amplitude ΔL _x = A _a − x _max1 − x _max2 between both beads during stretching and buckling averaged over several oscillation periods. (d) Theoretical mean amplitudes of the involved viscous forces (solid lines) compared to the experimentally obtained sum of all acting forces (markers) for a single trapped bead (yellow) and the filament – bead construct (red).