Figure 10.

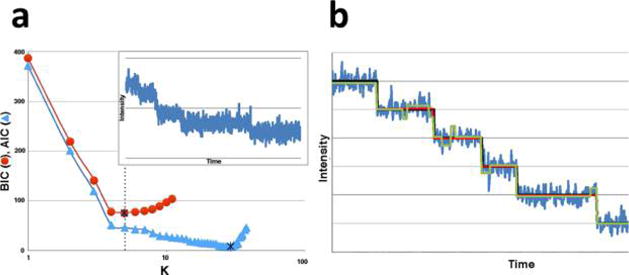
AIC and BIC are often both applied to step-finding. (a) We generated 1000 data points with a background noise level of standard deviation σ_b = 20. On top of the background, we arbitrarily added 6 dwells (5 points where the mean of the process suddenly changes) with noise around the signal having a standard deviation of σ_s = 5 (see inset). At this high noise level, and for this particular application, the BIC outperforms the AIC and the minimum of the BIC is at the theoretical value of 5 (dotted line). This is because the AIC overinterprets noise. All noise is Gaussian and uncorrelated. (b) Here we show another synthetic time trace with hidden steps, generated in the same manner as the data set in (a). The AIC (green) finds a model that overfits the true model (black), while the BIC (red) does not. However, as we increase the number of steps (while keeping the total number of data points fixed), the AIC does eventually outperform the BIC. This is to be expected. The AIC assumes the model could be unbounded in complexity and therefore does not penalize additional steps (model parameters) as much. The BIC, by contrast, assumes that there exists a true model of finite complexity. The data set for this simulation was generated via a Python implementation of the Gillespie algorithm, while both the BIC and AIC were implemented via elementary Python scripts.