Figure 15.

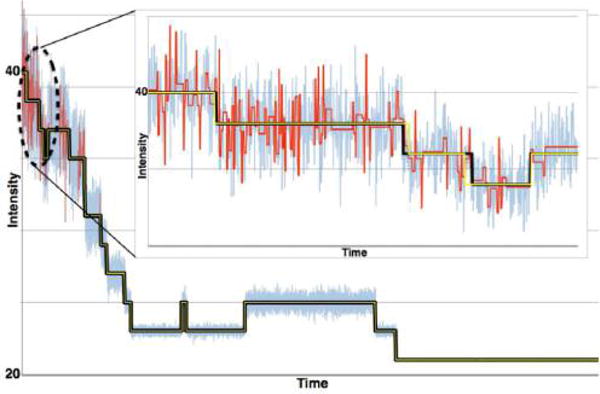
Successful Bayesian step-finding algorithms used in photobleaching use priors informed by the fluorophore photophysics. Here we present a noisy synthetic photobleaching time trace (blue) and the underlying true noiseless signal (black) for a set of 10 fluorophores that eventually all photobleach. Too many steps are found from an algorithm that assumes a constant noise profile (red) grossly overfitting the start of the trace where the noise level is at its highest. Results (yellow) of the Bayesian algorithm proposed by Tsekouras et al.,⁹⁶ which is tailored to photobleaching and assumes that noise grows along with the number of active fluorophores, are much more accurate. Inset: a blow-up of the first 1000 data points in this time trace where noise is highest and constant-noise algorithms overfit. The data set was created with a simple Gillespie algorithm using a variable signal-to-noise ratio. The code implementation of the method in ref 96 can be found online at https://github.com/lavrys/Photobleach. The code for the algorithm that does not take into account variable noise can be found at https://github.com/knyquist/KV_SIC.